Essence Of School Mathematics Education In Russia: Prospects Of Development

Abstract

The problem of the contents of school mathematics education in Russia is being updated. In our days, as a result of several educational reforms, the situation has changed. More attention in Russian and foreign educational practice is paid to improving technologies, increasing students’ interest in mathematics, sometimes at the expense of proper training. The article describes current state of the quality of mathematical knowledge of students in Russia, which has tended to decrease in last years. The authors reveal lack of fundamental training, insufficient level of practice-oriented knowledge and skills, poor development of meta-skills; study attitudes of participants in the educational process to teaching mathematics, their opinions on the relevance of various components of the mathematics programme at school. The results of the study and an analysis of world educational trends led to the following conclusions about the prospects for the mathematics education in Russia. These shall include an update of the content aimed at the intellectual development of students; mastering fundamental mathematical knowledge and skills necessary for practical application, for the study of related disciplines, for continuing education; development of meta-skills required for a full life in society. The technologies of electronic and blended learning, considering the specifics of mathematical activity, are defined as a means of updating the content of mathematics education.

Keywords: Maths educationcontentfundamental approachpractice orientationmeta-skills

Introduction

Russian mathematical school education undergoes crisis right now. Traditions of the Russian mathematical education rooted in a serious fundamental basis are being displaced by new requirements and fade due to the reform of the system of evaluating educational results.

The mathematical education may be seen as the process: pupils accumulate experience of applying their cognitive abilities in aggregate with meta-subject and personal qualities acquired during training. At present, there is still no unified approach to what shall constitute the content of education. Scientists from different countries sometimes have contradictory positions in addressing this issue. Mathematics at schools is suffering a number of changes associated with one of the world educational trends, namely, the enhancement of meta-skills of students. “The 21 ^st century skills development in the contents of school programme” is emphasized in different studies ( Gravemeijer et al., 2017). Yet, Gorbachev ( 2018) in his study (2018) discusses the general subject fundamentals of mathematical education, but does not take into consideration intersubject aspects.

Many researchers investigate the priority of practical orientation when teaching mathematics: Abramovich et al. ( 2019) consider the idea of learning through practice, through one’s own experience, practical projects. The authors argue that abstract mathematics leads to problems in communication with the theorized mathematics being not effective. This position is close to the point of view expressed earlier by Brady et al. ( 2015).

Another trend of the modern world education is gamification. Carbajal and Angulo ( 2019) suggest gameplay: as students resolve the situation, they obtain “experience points”. Such skills (also called as “habits of mind”) comprise “being open-minded, ability to think creatively, applying past knowledge to new situations, using systematic methods to problem analysis, classifying ideas, looking for different ways to solve the task/problem” ( Carbajal & Angulo, 2019, p. 7). Study at Jakarta school in Indonesia has shown that “impact of developed habits of mind toward mathematical ability is 40%” ( Dwirahayu et al., 2017, p. 5). The researchers also cover the efficiency of gamification while teaching numeracy in New Zealand primary school ( Nand et al., 2019).

Having analysed mathematical education reforms in the Netherlands, the researchers castigate them and propose a reorientation towards deeper, truly mathematical problems ( Gravemeijer et al., 2016). Testov ( 2017) underlines the importance of fundamentality of mathematical education, which has been traditionally eulogized in Russia, which is a seal of excellence of the Russian educational system. The author highlights that for determining the programme it is important to single out invariants which are 1) basic for a modern mathematical science, 2) accessible, 3) internalised by students. Having taken in this fundamental base, students can successfully master the subject area and even construct new knowledge.

In the context under study, Asian works on the development of mathematical thinking of students are also of interest. Mathematical thinking is given high priority in classroom, which is seen as an important feature of Chinese mathematics education ( Zhang, 2010).

The analysis of existing tendencies questions prospects of school mathematics education in Russian and the solution of the problem what it shall consist of to withstand the future challenges, to cater to world educational needs.

Problem Statement

The analysis of research and educational practice shows that there has been a rejection of fundamentality in the mathematical education, the focus has been shifted to meta-skills and it is their formation that modern educational technologies are directed to. The prevalence of only one of the constituents is not constructive. Strengthening of one of the parties of education leads to “failure” of the others. Obsession with technologies and methods to increase the interest of students coupled with excessive fixing on meta-skills often deteriorates the quality of subject training. Let us define the problem of specifying the actual content of school mathematics education oriented to the future.

Research Questions

What basic components of the programme are topical at a modern stage of the development of Russian mathematics education?

How do components of the mathematics education programme influence the quality of mathematical competence of school students?

How does the subject matter of school mathematics education affect readiness of students for continuation of mathematics education in higher school?

Purpose of the Study

The purpose of the study is to reveal prospects of development of the school mathematics education in Russia taking into account domestic traditions and world educational trends.

Research Methods

To find answers to the questions raised we used theoretical and empirical methods, the former include analysis of scientific literature, systematization and generalization of scientific search results, the latter – questionnaires, interviews, expert evaluation method, self-assessment, analysis and interpretation of results.

The result of the theoretical research was the identification of the main world trends as regards school mathematics education programme: practical orientation of content; involvement of students in solving real life problems; cognitive development (creativity, analytical thinking, etc.) of students, supporting their being independent in various situations of the future; fundamentality as a prerequisite of high quality education; development of meta-skills as immediate results of modern education.

To get an objective picture concerning applicability of certain components in Russian modern school programme of mathematics we have done the survey of participants of educational process. In 2016-2019 we continuously surveyed our respondents: 1,579 students of 10 ^th grade, 1,020 freshmen, 364 teachers of mathematics of general secondary schools in Krasnoyarsk Krai and Republic of Khakassia, 247 lecturers of mathematical disciplines of four Russian universities: Krasnoyarsk State Pedagogical University named after V.P. Astafyev, Siberian Federal University, Khakas State University named after N.F. Katanov, Financial University under the Government of the Russian Federation. The surveyed students are 15-19 years old, while the average age of the teachers and lecturers is 49 years.

The purpose of the student survey was to gather their opinions on issues related to the content of mathematics education: 1) attitude towards the knowledge, skills and abilities that students acquire; 2) personal expectations of their results of mathematical training at school. Survey assessed their understanding of what they should be taught, and which learning material is more effective and valuable to them. They also had to answer the questions to clarify the elements of mathematics education. The scale of answers was as follows: 0 – I find it difficult to answer; 1 – no; 2 – rather no than yes; 3 – rather yes than no; 4 – yes. A fragment of the questionnaire is presented in Table 1 .

The questions for teachers and lecturers were similar to those for students, providing different perspectives on the same elements of mathematics education to be considered. Below is a fragment of the questionnaire for teachers with the same set of answer options (Table 2 ).

Similar questions were to be answered by students and lecturers. This sample allowed us to compare the views of students of 10 ^th grade and freshmen, as well as the opinions and lecturers of higher school on the mathematics education, its components and their importance.

A comprehensive diagnostic work was used as a tool to determine the impact of the certain components of mathematics at school on the quality of students’ mathematical training. The results are shown in Table 3 .

The diagnostic work consisted of four sections: Algebra, Geometry, Real Mathematics and Meta-skills. The first two sections included assignments from the open bank of the basic state exam, which implies checking the basic knowledge and skills acquired during the main school course. When performing these tasks, students demonstrated knowledge of basic algorithms, key content elements (mathematical concepts, properties of mathematical objects, methods of solving typical problems, etc.), knowledge of mathematical language. Real Mathematics contained tasks from the open segment of PISA research, designed to assess the ability to apply the obtained mathematical knowledge in everyday life situations. Meta-skills contained the tasks of design and research character, revealing the ability to demonstrate knowledge of meta-skills of the 21 ^st century. An example of such a task is given below.

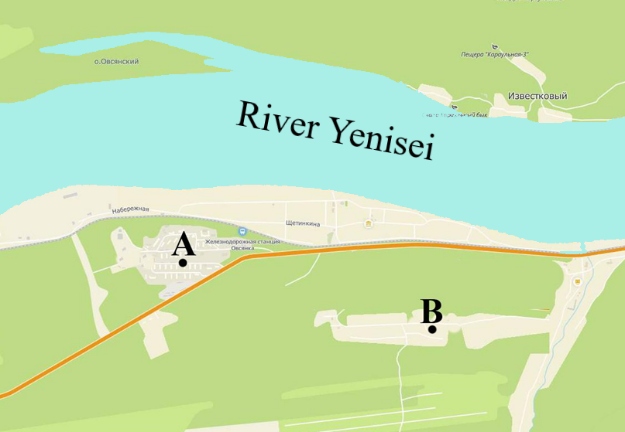
Task: An Internet provider plans to set a point of presence near two settlements and chooses the optimal place for its location. Using the proposed plan (Fig. 1), find the necessary point so that the length of both fiber optic cables to settlements A and B shall be the shortest.

See Full Size >

The tasks in first three sections were a test with open and multiple choice questions, questions to which students had to give short and expanded answers. This part was to be completed in 60 minutes. Each task scored one point provided that it was done correctly (the correct answer was written or selected, the elements of two sets were matched correctly, the corresponding sequence of numbers (in matching tasks) was found) and zero if the task was not done or done incorrectly.

The section Meta-skills was offered for small groups (3-4 people). The groups were formed randomly, the time was 30 minutes, the result was a written report. The work of the groups was observed by experts, who recorded the process of participants’ activity. Demonstration of the skills comprising this section was assessed on the basis of the actions made by the group members: clarification of the purpose of the activity, creation of the project idea and its concretization, drawing up the plan for the idea realisation, choice of the method for team work, coordination of actions with other people, ability to compromise, etc. Experts evaluated their strategic behaviour, taking into account non-participation in the process, isolated work, joint cooperation; ability to adapt to changing or unexpected situations, reaction to these situations, ability to adjust the activity strategy to new conditions. Also, the observants analysed the participants’ communication during the assignment and their reactions to the remarks of other team members. The ability to “make judgements and take decisions” was assessed according to the mathematical context of the task. The task completion was assessed by the experts with the help of a scale: if the skill was shown it was scored as 1 point, not shown – 0. Partial demonstration of skill was rated as 0.5 points. The maximum score for the whole task was 5 points.

The work was carried out in the academic years 2016-2017, 2017-2018 and 2018-2019 and involved 10 ^th grade students tested at the beginning of the academic year (in September-October). All in all, 278 schoolchildren from two regions participated in testing.

The readiness for further mathematical education is a very important factor of the mathematical education of secondary school leavers who continue to study engineering, economics, pedagogy, science, etc. at university, which requires plunge into higher mathematics. This is a complex characteristics that includes cognitive, activity-based, motivational and reflexive components ( Tabinova & Shashkina, 2016). The information on the readiness of secondary school graduates to continue their mathematical education was collected at the beginning of 2018-2019, 2019-2020 academic years. At this stage of the study it was possible to survey 65% of students who participated in the previous study during their school training. The following criteria were used in assessment: 1) subject knowledge and skills; 2) ability to learn and organize educational activities; 3) respondents’ evaluation of the importance of the quality of school mathematics training for the success in higher education institutions; 4) ability to adapt to studying in a new educational environment. In order to assess the subject knowledge and skills, we monitored the performance of students who entered higher education institutions. There were recorded results of the current and intermediate assessments in mathematical subjects. Ability to learn, evaluation of the importance of mathematical training and the ability to adapt were examined through questionnaires on Google forms. Students were offered a questionnaire of 25 questions, which were concentrated on the main positions related to the skills and ways of organizing learning activities. They were asked to make a self-assessment for each of the presented positions and tick whether it was mastered in the process of school education, independently or in the process of university education. The first-year students had to range the main components of the studied at school mathematics course by the degree of its importance for the study of higher mathematics at the university and future professional activity. Also, respondents assigned points based on the following parameters: 0 – irrelevant skill; 1 – infrequently used skill; 2 – necessary, frequently used skill.

The ability to adapt to learning at the university was kept track of according to the following parameters: consistency and continuity of the mathematics education in school and university courses, process of getting used to the new regime of educational activity, favourable communication outcomes as regards new participants in education, satisfaction of expectations about the selected university and the direction of training.

Findings

The results of the students’ survey showed that the majority of them (87.5%) would like to study “useful” mathematics, acquire mathematical knowledge, skills and activities that would be of advantage for them in everyday life, in their future professions, in university studies. They do not want to study abstract theories just for knowledge. The obtained results correlate with those of T.E. Dobie ( 2019). At the same time, as noted by the respondents (76.9%), when studying mathematics, they learn information, the application of which they do not understand. 87.7% of respondents said that learning mathematics contributes to the development of personal qualities and helps them to master the skills and activities that will help them in their future lives. Finally, only 7.4% of respondents believe that learning mathematics is a waste of time.

An analysis of teachers’ answers to the questions asked showed that the majority of mathematics teachers surveyed (84.3%) were focused on students’ achievements. This is because their professional competence is assessed on the basis of results of tests including mainly knowledge of subject matter and corresponding skills. Not many respondents (34.7%) pay heed to the practical application of studied mathematical knowledge and skills. Even fewer (27.9%) use the potential of the discipline to form and develop meta-skills of students.

Students expressed an opinion similar to that of schoolchildren. University lecturers, in contrast to school teachers, believe that cognitive development of students is no less important component of the content of school mathematics education as compared to subject knowledge and skills.

Analysis of the received data made it possible to calculate the percentage of completion for each section of tasks, which is shown in the bar chart (Figure 2 ).

See Full Size >

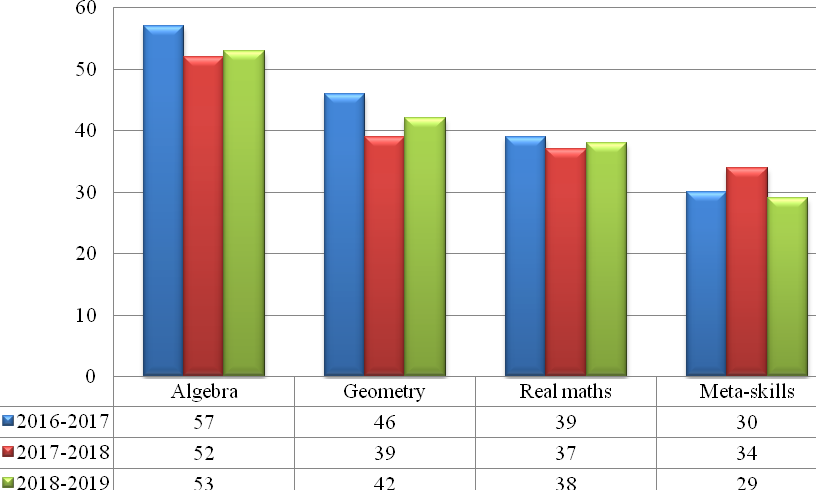
Schoolchildren experience serious problems with the task 16 aimed at assessing meta-skills and the tasks from Real Mathematics (tasks 11-15). The situation with the tasks from Geometry is a little better. Slightly more than half of the schoolchildren coped with Algebra completely (tasks 1-5).

The main mistakes were as follows: 1) computational errors and incorrect transformations of algebraic expressions; 2) inability to apply the main properties, definitions and formulas; 3) incorrect use of properties and features of geometrical figures; 4) inability to build a mathematical model according to the problem statement; 5) ignorance of methods and techniques of solving equations, inequations and their systems; 6) inattentive reading of the situation in the task.

The low percentage of solvability of tasks from Meta-skills and Real Mathematics indicates the inadequate practical orientation of school mathematics. But pursuing practical knowledge is obviously insufficient to acquire mathematical skills necessary for successful continuation of mathematical education at a university. The results assessing the level of readiness of school leavers to continue their mathematical education are shown in the diagram (Figure 3 ).

See Full Size >

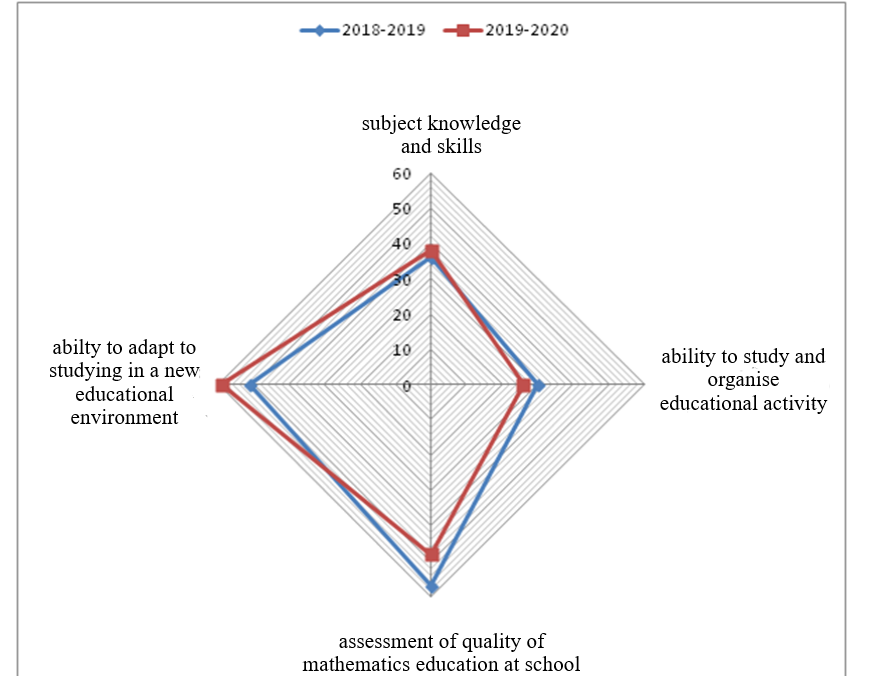
Many school graduates, including those who received 70 and above points at the unified state exam, admitted having difficulties in studying mathematical disciplines during their first university year. Having assessed the dynamics of freshmen’s performance, we found that the most students had the same problems in the same subject area as schoolchildren. Thus, in the process of school training a plenty of teenagers do not get a fundamental cognitive base, which would facilitate their mathematical education at university, which would develop the ability and willingness to use mathematical methods in their future professional life. In addition, in the 21 ^st century it is imperative for a person to master their meta-skills that are employed in any activity. Meanwhile, the results prove that this aspect has not been sufficiently learned (not more than 34 %). The content of mathematical training plays a key role in the process of adaptation of first-year students, it may enhance their academic success and efficiency of learning mathematical disciplines. The decreased quality of mathematics education at school distinctly reduces the efficiency of the educational process at university and quality of professional training in general.

Conclusion

The undertaken research allows us to assert that today there is a crisis situation in the Russian mathematics education. The participants of educational process have no uniform opinion on what should constitute school mathematical education, they judge the content and estimate its importance differently. The results clarified the following positions of the participants of the educational process: schoolchildren and students are aimed at the study of mathematical knowledge that would be useful for them in everyday life, in future profession, during university studies; teachers see their target in achieving high subject results by their students; university lecturers are focused on cognitive development of students. The mathematics teachers and university lecturers do not demonstrate any consensus in their views, and this is a problem area that requires separate research. Teaching essentials of subject is often done quite formally, the pedagogues teach routine solutions, skills, and typical algorithms for solving certain types of educational problems. The Russian educational paradigm lacks traditions of Soviet system, one of which was the fundamentality that would lay the foundation of mathematical content of students; they would certainly use this knowledge in life, since it enhanced the development of logic, algorithmic activity and thinking. Turning to the practical orientation, the content shall not be reduced to learning outcomes; it shall be intensified via teaching mathematical modelling and universal mathematical methods. At the same time, the creation of meta-skills in the process of teaching is relevant, too, as they are practically not supported by the content. Education is reformed mainly via technology improvement, but at the forefront should come the renewal of content, which would shape all components of the educational process. Development of school mathematics education in Russia shall be based on domestic traditions and world educational trends; a balanced combination of fundamentality and practical orientation. A purely pragmatic approach does not seem constructive. When schoolchildren have got a fundamental subject base, it is possible to develop their meta-skills more productively, which will allow them to continue their mathematical education in higher school and succeed in profession.

At the same time, new educational technologies serve as a tool to achieve the stated positions. These include digital and blended learning. “Multilevel electronic educational resources used in blended learning help to avoid the states of monotony, fatigue, anxiety, and contribute to a higher level of students’ involvement in learning activities” ( Shishova & Solobutina, 2019, p. 685). The usefulness of learning videos for studying mathematical reasoning, especially in geometry, is proved by the most recent studies ( Rasiman et al., 2020). Digital content is useful for discrete skill and content instruction such as math. In focus groups, students reported “feeling more accomplished when using digital content for math, also because they were given personalized tasks calibrated to their level and needs” ( Fazal et al., 2020, p. 76). Planned activities, the use of specialized resources such as Khan Academy (backed up by constant training of knowledge got) and academic virtual counselling might be a tool to help students in math class ( Gómez-Zermeño & Franco-Gutiérrez, 2018, p. 70). The study ( Neuper, 2019) describes the collaboration of computer methods with educational science. In the end, while teaching mathematics, computer and digital environment should provide a means for cognition and research of mathematical models and objects, so that against automation and technologization of activity there shall be no loss of understanding of the essence of mathematics.

References

• Abramovich, S., Grinshpan, A. Z., & Milligan, D. L. (2019). Teaching Mathematics through Concept Motivation and Action Learning. Education Research International, 2019, 3745406. https://doi.org/10.1155/2019/3745406
• Brady, C., Eames, C., & Lesh, D. (2015). Connecting real-world and in-school problem-solving experiences. Quadrante, 24(2), 5–36.
• Carbajal, R. M., & Angulo, C. V. (2019). Role Playing Games for Mathematics Education. Education in the Knowledge Society, 20, 7–13.
• Dobie, T. E. (2019). Expanding conceptions of utility: middle school students’ perspectives on the usefulness of mathematics. Mathematical Thinking and Learning, 21(1), 28–53. https://doi.org/10.1080/10986065.2019.1564969 
• Dwirahayu, G., Kustiawati, D., & Bidari. I. (2017). Corresponding Habits of Mind and Mathematical Ability. Journal of Physics: Conference Series, 895, 012013. https://doi.org/10.1088/1742-6596/895/1/012013
• Fazal, M., Panzano, B., & Luk, K. (2020). Evaluating the Impact of Blended Learning: a Mixed-Methods Study with Difference-in-Difference Analysis. TechTrends, 64, 70–78. https://doi.org/10.1007/s11528-019-00429-8
• Gómez-Zermeño, M., & Franco-Gutiérrez, H. (2018). The Use of Educational Platforms as Teaching Resource in Mathematics. Journal of Technology and Science Education, 8(1), 63–71. https://doi.org/10.3926/jotse.337
• Gorbachev, V. I. (2018). Content of the logical and conceptual competency of the general mathematical education (general subject bases). Science and school, 5, 23–34. [in Rus.]
• Gravemeijer, K., Stephan, M., Julie, C., Lin, F. L., & Ohtani M. (2017). What Mathematics Education May Prepare Students for the Society of the Future?  International Journal of Science and Mathematics Education, 15(Suppl 1), 105–123. https://doi.org/10.1007/s10763-017-9814-6
• Gravemeijer, K., Bruin-Muurling, G., Kraemer, J. M., & Stiphout, I. (2016). Shortcomings of mathematics education reform in the Netherlands: a paradigm case? Mathematical Thinking and Learning, 18(1), 25–44. https://doi.org/10.1080/10986065.2016.1107821       
• Nand, K., Baghaei, N., Casey, J., Barmada, B., Mehdipour, F., & Liang, H. N.  (2019). Engaging children with educational content via Gamification. Smart Learning. Environments, 6, 6.  https://doi.org/10.1186/s40561-019-0085-2 
• Neuper, W. (2019). Technologies for «Complete, Transparent & Interactive Models of Math» in Education. In P. Quaresma, & W. Neuper (Eds.), Theorem proving components for Educational software (ThEdu’18) EPTCS 290 (pp. 76–95). https://doi:10.4204/EPTCS.290.6
• Rasiman, A., Prasetyowati, D., & Kartinah, A. (2020). Development of learning videos for junior high school math subject to enhance mathematical reasoning. International Journal of Education and Practice, 8(1), 18–25. https://doi:10.18488/journal.61.2020.81.18.25
• Shishova, E. O., & Solobutina, E. M. (2019). E-Learning Based on Student’s Psychological Characteristics. In Conference: IFTE 2019 – 5th International Forum on Teacher Education (pp. 677–687). https://doi.org/10.15405/epsbs.2020.01.74
• Tabinova, O. A., & Shashkina, M. B. (2016). Diagnostics of the school leavers readiness to continue mathematics education. Standards and monitoring in education, 4(3), 8–13. [in Rus.]
• Testov, V. A. (2017). Content of modern education: a choice of path. Education and science, 19(8), 29–46. https://doi.org/10.17853/1994-5639-2017-8
• Zhang, D. (2010). The features of mathematics education in China. People’s Education, 1, 36–38. [in Chinese]