The Developmental Changes In Number Sense Throughout The School-Age

Ilya Zakharov ,
Elena Shvets ,
Zalina Takhirova ,
Elsa Khusnutdinova

Abstract

Number sense is an intuitive understanding of numbers magnitude, relationships between numbers and the way they are affected by different operations. It has been shown to be an important factor for the success in STEM fields. The aim of the present study was to investigate the developmental changes in non-symbolic number sense throughout the school age. The sample included Russian schoolchildren from multiple general education institutions with total 1169 participants. The results have shown that age was significant predictor for Number Sense total score, median response time and response time variance. The R2 was highest for the RT variance.Number sense accuracy increase and response time characteristics decrease with age. The response time variance showed the most prominent changes with age.The processing speed characteristics variance decline among pupils with an increase in educational level. At the same time number sense accuracy variance increased in higher grades (though there were decline at the age of 14 in the 9th grade). Within-grade variance in numbers sense precision not only remain high throughout the school-age, but even increase with an increase in educational level. Higher individual difference among adolescents comparing to younger children may be related to non-cognitive factors, such as emotional development.

Keywords: Number sensedevelopmental changesadolescentsmathematical ability

Introduction

In the recent decades mathematical abilities have become a subject to intensive research due to the growing importance of STEM field. One of the still unresolved issues is what shape future success and failure in maths-related performance. The cognitive system that is supposed to be a foundation to our numerical intuitions and later mathematical abilities has been called the approximate number system (ANS). Part of the ANS is number sense which can be defined as an intuitive understanding of numbers magnitude, relationships between numbers and the way they are affected by different operations. It has been shown to be involved in generation of nonverbal representations of numerosity in nonhuman animals (Merritt, DeWind& Brannon, 2012) and is present in human since infancy (Izard, Sann, Spelke&Streri, 2009). The number sense has been shown to be moderately heritable and is supposed to be under directional evolutionary selection (Brannon, 2006; Tosto et al., 2014). Number sense and ANS includes the ability to operate with symbolic and nonsymbolic quantities. In the present article we are focused on the nonsymbolic ANS (Halberda et al., 2008).

The ANS has been repeatedly shown to be linked to formal mathematics in children (Malykh et al., 2017; Tikhomirova et al., 2014; Desoete, Ceulemans, De Weerdt, Pieters, 2012; Gilmore, McCarthy &Spelke, 2010; Halberda, Ly, Wilmer, Naiman&Germine, 2012), though the exact pattern of relationship is still to be confirmed (Tikhomirova et al., 2015; Inglis, Attridge, Batchelor& Gilmore, 2011; Soltész et al., 2010). Starr and colleagues have shown, that even the earliest measures of preverbal number sense can be predictive for standardized maths ability 3 years later(Starr et al., 2013). Marle has shown that the acuity of the inherent ANS in preschoolers was significantly correlated with mathematics achievement following one year of preschool, and predicted performance on measures of children's explicit knowledge of Arabic numerals, number words, and cardinal value, controlling for age, sex, parental education, intelligence, executive control, and pre-literacy knowledge(Marle et al., 2014). Tikhomirova with colleagues in a longitudinal study showed cross-lagged associations between number sense and the success in learning mathematics at primary school age(Tikhomirova et al., 2018).

Problem Statement

Though individual differences in number sense has shown to be present since infancy and remain throughout the life course, developmental changes have rarely been tested. Park and colleagues has shown that sensitivity to numerical magnitude, absent at three, increases as a function of age (Park, 2018). A numerosity comparison was also shown to be developing steadily in early childhood from 3 years old (Halberda & Feigenson, 2008; Piazza et al., 2010; Halberda et al., 2012; Mussolin et al., 2012). These development is in agreement with the changes at the neural level, particularly in the posterior parietal cortex which is sensitive to numerosity (Arsalidou et al., 2018; Cantlon et al., 2006; Izard et al., 2008; Hyde & Spelke, 2011; Libertus et al., 2011). It was also shown that number sense is influenced by formal mathematical education (Park & Brannon, 2013, Fiegenson et al, 2013). However, the effect of formal education has been studied only for the symbolic but not nonsymbolic number sense.

The trajectory of changes in the ability to manipulate nonsymbolic quantities has been systematically studied by the group leaded by Halberda. They investigated development of ANS in a massive internet-based study with the ANS dot test (Halberda et al., 2012). The overall sample included 3000 participants from 11 to 85 years. According to their data, the precision of one’s number sense improves throughout the school-age years and continues later in life with peak at as late as 30 years old. It was also shown that very large individual differences are present among people at the same age throughout adolescence and the adult years.

Research Questions

Purpose of the Study

The purpose of the present study is to assess the development of the nonsymbolical number sense throughout the school age in non-selected sample of Russian school children from general education institutes. The analysis of the nonsymbolical mathematics abilities is an important part of understanding the individual difference in STEM-related activities.

Research Methods

Participants

The sample included schoolchildren from multiple general education institutions from different regions of Russian Federation with total 1169 participants. The data of 1169 school students from 1st to 11th grade was analyzed. The median age of participants was 11 years (SD = 3.16, 61% boys). The analysis was carried out on the basis of anonymous personal data.

Methods

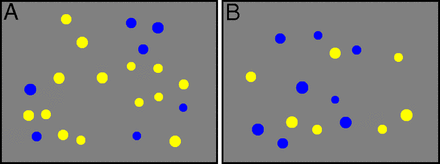
In the Number Sense Task, yellow and blue dots different in size are presented on the screen (Halberda et al., 2008; Tosto et al., 2013). The children were asked to the participant report whether there were more blue or more yellow and press the corresponding key on the keyboard. The stimuli contained 150 static images with arrays of yellow and blue dots, the number of which varies from 5 to 21 points of each color. The image appears on the screen for 400 ms, maximum response time is 8 seconds. The test consists of three blocks of 50 tasks. The ratio of dots of two colours was either 1:3 or 6:7. This judgment is easy with larger ratio but becomes more difficult when the ratio of blue to yellow dots is close (Fig. 1). By varying this ratio across trials, it is possible to determine the precision of an individual’s ANS. The accuracy of response and response time is recorded. We used the total score (NS Total score) as the measure of the number sense ability. We were interested in the efficiency of the task performance, so we also calculated the response time characteristics. We have chosen the median response time (NS RT) as it has been shown to be more stable estimate than mean and the response time variance (in intra-individual standard deviation) as a measure of processing speed (Jensen, 1992)

Figure 1: (A) A trial from the Number sense test with higher yellow to blue ratio. There are more yellow dots in this trial. (B) A trial from the Number sense test with lower yellow to blue ratio. There are more blue dots in this trial.
(A) A trial from the Number sense test with higher yellow to blue ratio. There are more yellow dots in this trial. (B) A trial from the Number sense test with lower yellow to blue ratio. There are more blue dots in this trial.
See Full Size >

Statistical approach

We used statistical language R 3.4.0 (R Core Team, 2017) for data analysis. The yarr package (https://CRAN.R-project.org/package=yarrr) was used for descriptive statistics evaluation, lm.beta package (https://CRAN.R-project.org/package=lm.beta) were used for linear regression. For regression analysis single linear models were constructed for each measure with age as predictor.

Findings

Results

Table 1 -
See Full Size >

The pirate plots (https://CRAN.R-project.org/package=yarrr) of the variables are shown in figure 2 . Pirate plot is the RDI ( Raw data, Descriptive statistics, and Inferential statistics) plot displaying the relationship between independent and dependent variable.

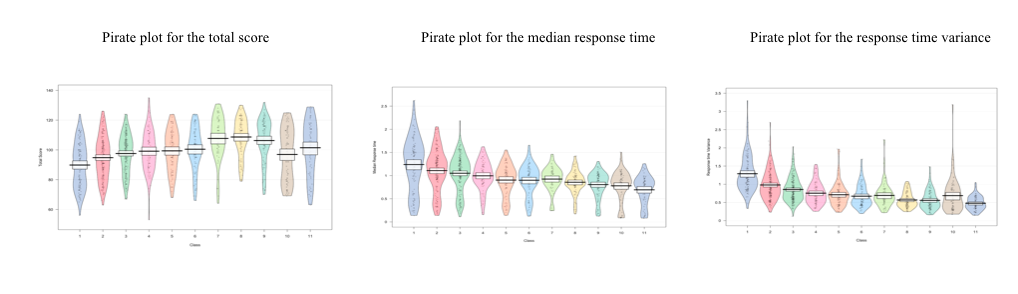
Figure 2: Pirate plots for total score, median response time, and response time variance (from left to right). A pirate plot has 4 main elements: points, symbols representing the raw data (jittered horizontally); bar, a vertical bar showing central tendencies (in the present data the medians were calculated); bean, representing a smoothed density; and a rectangle representing an 95% confidence inference interval.
Pirate plots for total score, median response time, and response time variance (from left to right). A pirate plot has 4 main elements: points, symbols representing the raw data (jittered horizontally); bar, a vertical bar showing central tendencies (in the present data the medians were calculated); bean, representing a smoothed density; and a rectangle representing an 95% confidence inference interval.
See Full Size >

The main goal of the study was to investigate whether different characteristics of Number Sense varies as a function of age. We have found that age was significant predictor for Number Sense total score, median response time and response time variance. The R2 was highest for the RT variance. The results of the simple linear regression models are presented in Table 2

Table 2 -
See Full Size >

We were also interested in the changes in variance in non-symbolic number sense. There are several methods to assess variance of the distribution. In the present study we have chosen standard deviation, interquartile range (IQR), and max-min difference. All the measures were estimated inter-individually and intra-class (within the class). We plot the measures separately for Total score and response time characteristics in figure 3 .

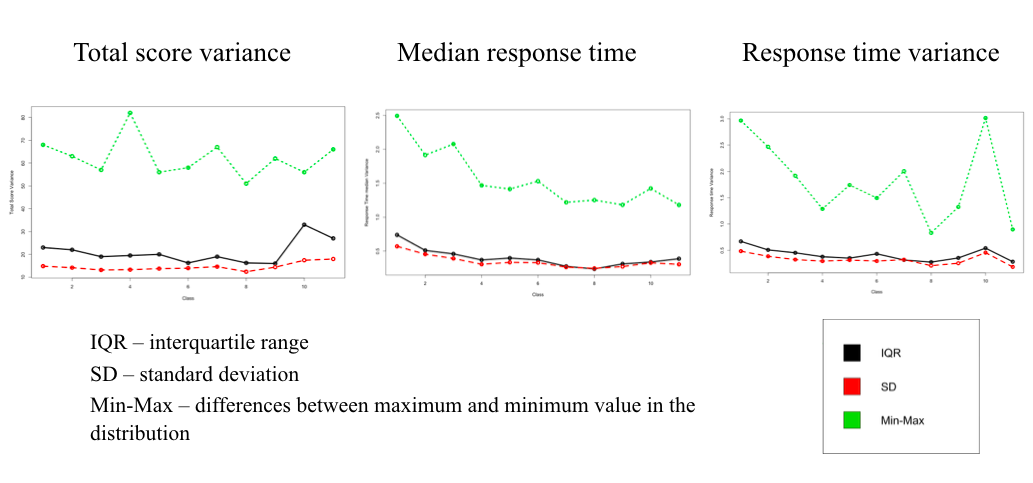
Figure 3: Class difference in total score variance, median response time and response time variance (from left to right). The x-axis is the number of grade. Green line - the difference between the maximum and minimum value within each grade, black line - the interquartile range, red line - standard deviation for each grade.
Class difference in total score variance, median response time and response time variance (from left to right). The x-axis is the number of grade. Green line - the difference between the maximum and minimum value within each grade, black line - the interquartile range, red line - standard deviation for each grade.
See Full Size >

Visual analysis of the graphs shows us that for the total score SD and IQR there is at first the decline in variance from 1st to 9th grade which changes to increase at 10th and 11th grade. The same pattern (though, with smaller increase) can be seen both for response time median and standard deviation. The graph for min-max is less inconsistent for all the measures. We used Bartlet K-test (Bartlett, 1937) to test whether the difference in variance is significant. For all the measures we found that variance is not homogeneous among grades (F(1,10)=22,7; 140,6; and 147,06; p<0.001, for total score, RT median and RT variance, respectively)

Discussion

In the present article we investigated the developmental changes in number sense throughout the school-age. We have found the significant association between increase in age and different characteristics of number sense. The ANS of our participants has become more precise with age (manifested in higher accuracy). The same pattern was found for the speed and quality of non-symbolic information processing (manifested in the faster response time and less variance between the answers). The developmental changes were most evident for the response time variance. These data are in agreement with the well-documented development of specific cognitive abilities and information processing characteristics in general (for example, De Luca et al., 2003).

We were also interested whether formal mathematical education result in the less pronounced individual differences in non-symbolic number sense abilities. In accordance with our hypothesis, we found that processing speed characteristics variance decline among pupils with an increase in educational level. At the same time we also discovered the opposite trend for number sense accuracy variance which has increased in higher grades (though there are a decline at the age of 14 in the 9th grade). De Luca with colleagues have found the same pattern for executive function capacities (De Luca et al., 2003). The increased individual difference among adolescents may be related to non-cognitive factors, for example, such as emotional development, personality traits (Steinberg, 2005; Malykh & Tikhomirova, 2015).

The significant limitation for our results is that our data was collected in cross-sectional design, that makes it impossible to track intra-individual developmental trajectories. For further studies, it is important to analyze the relationship between number sense and other other specific cognitive abilities in longitudinal design.

Overall, our results are comparable to the results of Halberda et al. (2012). High variability and broad confidence intervals in our sample didn’t allow us to determine precisely whether the numbers sense mean accuracy and response time shows developmental changes up to the very end of school age, but visual inspection of the data is in agreement with the results of the Halberda, who showed steady increase in number sense characteristics together with high degree of individual differences with peak at as late as ~30 years old. Here we repeated their findings in the less noisy and more-controlled samples from multiple general education institutions in Russia. The persistence of high variance among the ANS characteristics across broad age range are in line with the evidence of the directional selection for number sense hypothesized by Tosto (2014) and may indicate its importance for evolutionary success even in the modern world.

Conclusion

In the present study we reproduced the findings of Halberda and colleuages and have shown more evidence of steady increase in the non-symbolic number sense characteristics. We have also shown that variance in ANS precision not only remain high throughout the school-age, but even increase with an increase in educational level. Further studies combining more specific cognitive abilities characteristics  and longitudinal design are required.

Acknowledgments

This study was supported by the grant from the Russian Science Foundation № 17-78-30028

References

  1. Arsalidou, M.Pawliw-Levac, M.Sadeghi, M.&Pascual-Leone, J. (2018). Brain areas associated with numbers and calculations in children: Meta-analyses of fMRI studies.. Developmental Cognitive Neuroscience,, 49, 239-250
  2. Bartlett, M S. (1937). Properties of sufficiency and statistical tests.. Proceedings of the Royal Society of London Series A160,, 268-282
  3. Brannon, E M. (2006). The representation of numerical magnitude.. Current Opinion in Neurobiology,, 49(2), 222-229
  4. Cantlon, J F.Brannon, E M.Carter, E J.&Pelphrey, K A. (2006). Functional Imaging of Numerical Processing in Adults and 4-y-Old Children. PLOS Biology,, 49(5), 125-10
  5. Luca, C R De.Wood, S J.Anderson, V.Buchanan, J A.Proffitt, T M.Mahony, K.&Pantelis, C. (2003). Normative data from the CANTAB. I: development of executive function over the lifespan. Journal of clinical and experimental neuropsychology,, 49(2), 242-254
  6. Smedt, B De.Noël, M-P.Gilmore, C.Ansari, D. (2013). How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior.. Trends in Neuroscience and Education,, 49(2), 48-55
  7. Desoete, A, (). Desoete, A., Ceulemans, A., Weerdt, F. D., &Pieters, S. (n.d.). Can we predict mathematical learning disabilities from symbolic and non-symbolic comparison tasks in kindergarten? Findings from a longitudinal study. British Journal of Educational Psychology, 82(1), 64–81.
  8. Feigenson, L.Libertus, M E.&Halberda, J. (2013). Links between the intuitive sense of number and formal mathematics ability. Child development perspectives,, 49(2), 74-79
  9. Gilmore, C K.McCarthy, S E.&Spelke, E S. (2010). Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling.. Cognition,, 49(3), 394-406
  10. Halberda, J.&Feigenson, L. (2008). Developmental change in the acuity of the “number sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults.. Developmental Psychology,, 49(5), 1457-1465
  11. Halberda, J.Ly, R.Wilmer, J B.Naiman, D Q.&Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample.. Proceedings of the National Academy of Sciences,, 49(28), 11116-11120
  12. Halberda, J.Mazzocco, M M M.&Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement.. Nature,, 49(7213), 665-668
  13. Hyde, D, (). Hyde, D. C., &Spelke, E. S. (n.d.). Neural signatures of number processing in human infants: evidence for two core systems underlying numerical cognition. Developmental Science, 14(2), 360–371.
  14. Inglis, M.Attridge, N.Batchelor, S.Gilmore, C. (2011). Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children.. Psychonomic Bulletin & Review,, 49(6), 1222-1229
  15. Izard, V.Sann, C.Spelke, E S.&Streri, A. (2009). Newborn infants perceive abstract numbers.. Proceedings of the National Academy of Sciences,, 49(25), 10382-10385
  16. Jensen, A R. (1992). The importance of intraindividual variation in reaction time. Personality and individual Differences,, 49(8), 869-881
  17. Libertus, M E.Feigenson, L.&Halberda, J. (2011). Preschool acuity of the approximate number system correlates with school math ability.. Developmental Science,, 49(6), 1292-1300
  18. Malykh, S B.Lysenkova, I A.Zakharov, I M.Tikhomirova, . (2017). Cognitive predictors of academic achievement at high school age: cross-cultural study.. The European Proceedings of Social & Behavioural Sciences, XXXIII,, 235-247
  19. Malykh, S B.Tikhomirova, . (2015). Personality features and intellect: The nature of co-relation.. Voprosy Psychologii,, 49, 149-160
  20. Marle, K van.Chu, F W.Li, Y.Geary, D C. (2014). Acuity of the approximate number system and preschoolers’ quantitative development.. Developmental Science,, 49(4), 492-505
  21. Merritt, D J.DeWind, N K.Brannon, E M. (2012). Comparative Cognition of Number Representation. The Oxford Handbook of Comparative Cognition.
  22. Mussolin, C.Nys, J.Leybaert, J.Content, A. (2012). Relationships between approximate number system acuity and early symbolic number abilities.. Trends in Neuroscience and Education,, 49(1), 21-31
  23. Park, J. (2018). A neural basis for the visual sense of number and its development: A steady-state visual evoked potential study in children and adults.. Developmental Cognitive Neuroscience,, 49, 333-343
  24. Park, J.Brannon, E M. (2013). Training the Approximate Number System Improves Math Proficiency. Psychological Science,, 49(10), 2013-2019
  25. Piazza, M.Facoetti, A.Trussardi, A N.Berteletti, I.Conte, S.Lucangeli, D. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia.. Cognition,, 49(1), 33-41
  26. Rodic, M, (). Rodic, M., Zhou, X., Tikhomirova, T., Wei, W., Malykh, S., Ismatulina, V., … Kovas, Y. (n.d.). Cross-cultural investigation into cognitive underpinnings of individual differences in early arithmetic. Developmental Science, 18(1), 165–174
  27. Steinberg, L. (2005). Cognitive and affective development in adolescence. Trends in cognitive sciences,, 49(2), 69-74
  28. Soltész, F.Szűcs, D.&Szűcs, L. (2010). Relationships between magnitude representation, counting and memory in 4- to 7-year-old children: A developmental study.. Behavioral and Brain Functions,, 49, 13-
  29. Starr, A.Libertus, M E.Brannon, E M. (2013). Number sense in infancy predicts mathematical abilities in childhood.. Proceedings of the National Academy of Sciences,, 49(45), 18116-18120
  30. Tikhomirova, T.Kuzmina, Y.Malykh, S. (2018). Does symbolic and non-symbolic estimation ability predict mathematical achievement across primary school years?. ITM Web of Conferences,, 49, 4006-
  31. Tikhomirova, Malykh.Tosto, Kovas. (2014). Cognitive characteristics and mathеmatical achievement in high school students: cross-cultural analyses., 49(1), 55-68
  32. Tosto, M G.Petrill, S A.Halberda, J.Trzaskowski, M.Tikhomirova, T N.Bogdanova, O Y. (2014). Why do we differ in number sense? Evidence from a genetically sensitive investigation.. Intelligence,, 49, 35-46
  33. Tosto, M G.Tikhomirova, T.Galajinsky, E.Akimova, K.&Kovas, Y. (2013). Development and Validation of a Mathematics-number sense Web-based Test Battery. Procedia -. Social and Behavioral Sciences,, 49, 423-428

Copyright information

Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

About this article

Publication Date

23 November 2018

Article Doi

https://doi.org/10.15405/epsbs.2018.11.02.93

eBook ISBN

978-1-80296-048-8

Publisher

Future Academy

Volume

49

Print ISBN (optional)

-

Edition Number

1st Edition

Pages

1-840

Subjects

Educational psychology, child psychology, developmental psychology, cognitive psychology

Cite this article as:

Zakharov, I., Shvets, E., Takhirova, Z., & Khusnutdinova, E. (2018). The Developmental Changes In Number Sense Throughout The School-Age. In S. Malykh, & E. Nikulchev (Eds.), Psychology and Education - ICPE 2018, vol 49. European Proceedings of Social and Behavioural Sciences (pp. 815-823). Future Academy. https://doi.org/10.15405/epsbs.2018.11.02.93

Copy citation text