Application Of The Support Vector Machine In Solving The Credit Scoring Problems

Abstract

Scoring is one of the main tools in the banking system to determine the creditworthiness of customers. There are many methods for processing and storing customer information, but the effectiveness of these methods is related to the quality of the data provided and the process of their processing. In this regard, there is a need to study methods and find the optimal one. This article describes the possibility of using the support vector machine (SVM) to solve the credit scoring problems. The concept and essence of the SVM are considered. The support vector machine permits to build a good classifier with a minimum of initial features. In difference with other methods, the SVM is the most optimal for determining the creditworthiness of a client. We trained the sample on one set and checked on another test sample. As a result of testing the support vector machine (50 starts), a minimum error of 15.6% was obtained. The article also proposes a structural-functional model of the loan processing system using this method. The article describes the decision-making process for granting a loan in the form of a structural-functional model in the form of a diagram. The structural and functional model involves the application of the process of processing loan applications using the support vector machine as a software module in an automated banking system.

Keywords: Credit scoringsupport vector machine

Introduction

A scoring system is a special computer program that banks use for a qualitative assessment of customers based on the personal data of borrowers. The scoring model is a weighted sum of certain characteristics. The result is an integral indicator (score), the higher the indicator, the higher the customer’s reliability (Skupchenko & Semeykin, 2009). In turn, a bank can sort own customers by the degree of increase in creditworthiness. Any bank gives everyone customers a rating, thus compiling a customer rating. The software produces a result, which resolves the issue of granting a loan or refusing it.

The priority for formulating the credit scoring concept is usually given to David Durand. His research published in the National Bureau of Economic Research in 1941. The research contented 7200 «good» and «bad» credit histories of loans with regular repayments provided by 37 companies. He applied the chi-square criterion to identify characteristics that markedly distinguished «bad» from «good», and developed a performance index designed to demonstrate how effective this characteristic is to differentiate the degree of risk («good» or «bad») among loan applicants (Durand, 1941; How Borrowers Can Use TransUnion, 2015). Of course, this research permitted to form a modern system for assessment the creditworthiness of borrowers using mathematical models.

The large issue of credit cards stimulated the application of scoring by banks. As the number of people who applied for credit cards began to increase daily and banks needed to automate this process. The adaptation of the scoring system has led to the fact that not only the speed of processing the application for a loan has increased, but also the quality of risk assessment. According to many bank studies, the application of scoring systems helped to increase the bad debt level, which decreased to 50%, (Free Credit Reports, 2017; Yap et al., 2011).

Scoring advantages:

• to optimization of costs for consideration of the application by automating the decision-making process and issuing a loan;

• to reduction of the time for consideration of the application, that increase in the number and speed of processed applications;

• to absence of subjective opinion of an expert when deciding on a loan;

• to determination of the level of profitability and risk of the loan portfolio, etc.

• to identification and prevention of fraud attempts.

Scoring disadvantages:

• a program doesn’t evaluate a real person, but the information that provides about it. Thus, a well-trained client can present good information about you and this information guarantees to receive a loan;

• a credit rating is made on the basis of data on those borrowers for whom a loan was issued by bank (Volkova et al., 2017a, 2017b).

The scoring models require constant refinement and updating, since over time, both socio-economic and lending conditions and behavior of people change too. In this regard, there is a need to modernize the credit scoring system based on various data mining methods. This paper discusses the possibility of using the support vector machine (SVM) to solve credit scoring problems. The main goal of such programs minimizes costs and reduces operational risks through automation in the decision-making process. Thus, there is a need to find the optimal algorithm for optimizing credit scoring. Scientists are testing different automation algorithms; we will try to justify the need to using the support vector method for solving credit scoring problems.

The support vector machine (SVM) as a statistical classification method was proposed by Vapnik (1999). The work of V. Shen et al. is one of the first where the SVM was used to solve the credit scoring problem. The system of support vectors relative to the family of cores was used for credit scoring in the work of C. Lin (as cited in Hsu & Lin, 2002).

Statistically significant performance differences are identified using the appropriate test statistics. It is found that both the SVM and neural network classifiers yield a very good performance, but also simple classifiers such as logistic regression and linear discriminant analysis perform very well for credit scoring (Baesens et al., 2003).

The essence of the method is as follows. Let a learning set be given where

${\left\{\left[x^j;y^j\right]\right\}}_{j=\mathrm{1,2}\dots ,j,\mathrm{}\mathrm{}}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{}{x}^j\subset R$ is a feature description object, $y^j$∈{−1;1} is a binary classifier. Equation of the form ⟨w, x⟩−w0=0, w∈R defines a hyperplane with a normal vector w, which separates in the space Rn classes objects: «good» y(j)=1 and «bad» y(j) = –1.

The optimal dividing hyperplane is defined as the solution to the optimization problem: ‖w‖→min;

y( j)(⟨w , x( j)⟩−w0)≥1, j=1,2,... ,l .

In the case where a separating hyperplane exists, the value $\frac{\mathrm{2}}{‖w‖}$ is a width of the line between points of different classes. The problem of finding the optimal separating hyperplane is solved by using the Kuhn – Tucker theorem. Value L(w,w0,λ)= $\frac{\mathrm{1}}{\mathrm{2}}$⟨w ,w⟩— ${\sum }_{j=\mathrm{1}}^j{y}^j\left(〈w,\mathrm{}{x}^j〉-w_{\mathrm{0}}\right)-\mathrm{1}$ corresponds to the Lagrange function.

Training Sample Object x(j) is called a support vector if λ j>0 and ⟨w , x(j)⟩−w0=y( j)x(j).

Vector w is a linear combination of support vectors: ${\sum }_j{\lambda }^{\left(j\right)}{y}^{\left(j\right)}.$

Thus, for the actual construction of the vector w, a relatively small number of objects in the training set are used. This sparse property differ the support method from classical linear separators of the Fisher discriminant type. If the dividing plane does not exist (the training set is linearly not separable), the formulation of the optimization problem is adjusted. The amount of fines for errors is added to the objective function.

A transition to a nonlinear separator using a core is also possible. The core is understood as a function K(x, x'), x, x'∈X such that K(x,x')=⟨φ(x),φ (x')⟩ for some reflection φ : X →Rm. Using the reflection φ, the linear separator can be constructed in space Rm.

Parameters Cj control the relative value of indicators. The following nuclear functions are most commonly use K(x(i), x(j))= ⟨x(i), x(j)⟩– linear model;

K(x(i), x(j)) = (⟨x(i), x(j)⟩+1d) – polynomial degree model d;

K(x(i), x(j))=exp The Gaussian radial basis function with parameter is σ.

For a new object, the prediction is constructed according to the formula $\mathrm{y}=\mathrm{s}\mathrm{g}\mathrm{n}\left({{\sum }_j\lambda }_j{y}^{\left(j\right)}K(x^{\left(i\right)},\mathrm{}x)b_j\right),\mathrm{}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{}{b}_j={\sum }_j{\lambda }_j{y}^{\left(j\right)}K\left(x^i,x^{\left(j\right)}\right).$

The support vector machine permits to build a good classifier with a minimum of initial features. The main idea of the classifier on support vectors is to build a separating surface using only a small subset of points lying in the zone critical for separation, while the remaining correctly classified observations of the training sample outside this zone are ignored (more precisely, there are a «reservoir» for optimization algorithm). The search for a solution reduces to the convenient quadratic optimization problem with linear constraints, which is guaranteed to converge to one global minimum (Khemais et al., 2016; Lugger, 2004). Since the location of a hyperplane is influenced only by observations that lie on the boundaries of the gap or violate it, the decision rule of such a classifier is quite resistant to outliers of most points located outside the «critical zone» of separation (Louzada et al., 2011). This property distinguishes it from the properties of other classifiers.

Problem Statement

In modern time the scoring development in Russia is limited by lending volumes still low by Western standards, as well as rapidly changing political and economic conditions. Russian banks and rating agencies don`t have enough information about customers in order to build effective mathematical models that provide demand for retail lending, refinancing, on the one hand, and on the other hand minimizing bank risks.

Research Questions

Is the support vector machine optimal for solving credit scoring problems? What error does it produce when analysing data?

How can this method be installed in an automated banking system for processing loan applications?

Purpose of the Study

It is assumed that the support vector machine is optimal for using in a credit scoring. The structure of an automated banking system for issuing loans is considered and it is proposed to use SVM when processing data about the borrower, as it produces the smallest error in calculations and quickly analyses information than, for example, a neural network.

Research Methods

Credit scoring models helps to categorize the applicants into two classes: in one case the applicants are accepted and in other cases applicants are rejected (Korneev, 2001). The algorithms or models with less computational time are more efficient and thus gives more profit to the banks or firms. As a result various methods for the decision making of loan analysis have been proposed. The approach helps to detect fraud, assess creditworthiness presented the various classification techniques for credit scoring. An effective loan analysis also helps to issue loans with minimum risk (Hand & Henley, 1997; Hens & Tiwari, 2012; Weston, 2011).

At the first stage, data processing is performed by the client on the basis of a scoring card by a bank employee. Further, the loan agent brings information to the customer base (Figure 01 ).

Borrower data is transferred to an internal customer data warehouse. At this stage, the SVM enters the work on processing applications.

Then, the data is normalized on an unprocessed request. The process prevents the appearance of redundancy of the stored data; the data is always stored in only one place, which makes the process of inserting, updating and deleting data easy.

The next stage is a data-processing operation (at this stage, data from a scoring card is analysed). Denormalization of data permits to intentionally bring the database structure to a state that does not meet the normalization criteria to speed up read operations from the database by adding redundant data. In turn, data denormalization sends information checks to the internal repository of data about borrowers. Thus, a system accomplishes of a data-processing operation of the borrower application with the main aim of approving or not approving the loan (Figure 01 ).

See Full Size >

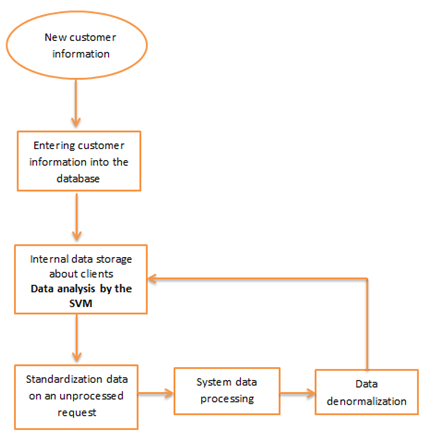
The SVM description: to implement the classification task, a function is used (function = fitcsvm), the algorithm is also implemented by the «Matlab» software, all data was provided by the bank's archive for 2018. The total number of applications for consumer loans from individuals received for processing was 100. All loan applications from borrowers were anonymous.

Function Description function=fitcsvm

fitcsvm trains or cross-checks the reference SVM model for one-class and two-class (binary) classification in a low or medium size predictor dataset. fitcsvm supports the display of predictor data using kernel functions and supports sequential minimum optimization (SMO), iterative single data algorithm (ISDA), or minimizing soft L1 fields using quadratic programming to minimize the objective function (Hu et al., 2012; Lugger, 2004).

To train the linear SVM model for binary classification on a multidimensional dataset, i.e. a dataset that includes many predictor variables, use fitclinear instead.

To train a multiclass with combined binary models SVM, we use error correction output codes (ECOC).

The division into test and random samples occurs randomly. The classification algorithm for the quality indicators of the decision gives the percentage of erroneous decisions. It is advisable to find the average value, coefficient of variation, standard deviation. The starting in the «Matlab» showed the following values (Figure 01 ):

See Full Size >

Next, we train the sample on one set and check on another test sample. We evaluate the work of starting this SVM algorithm. Based on the results of 50 starting, we obtain the following values (Table 01 ):

Findings

Learning by a neural network has an order of magnitude more complicated structure, because the program needs to select the appropriate number of neurons and hidden layers, so that the error is minimal. The neural network showed the result with 1 layer and 14 neurons, an error of 17.9%, despite the fact that 1 layer was taken and the launch took place 25 times. When using the SVM, a minimum error of 15.6% was obtained at the first start. SVM operates 2 times faster than a neural network; this is due to the nature of the support vector method. Therefore, the support vector method is the most suitable classification algorithm for the credit scoring procedure.

Conclusion

An analysis of past experiments showed that an artificial neural network processes the data on borrowers several times longer than the SVM. We assume that this method and the developed structural-functional model should be used in processing data on the issuance of consumer loans for small amounts. In general, a data processing mechanism has been proposed for the general automated bank system in the form of a structural-functional model based on the SVM, which shows the stage of processing data of the support vector machine.

Acknowledgments

We would like to thank the Department of System Analysis of the Institute of Informatics and Telecommunications of Reshetnev Siberian State University of Science and Technology for constructive comments on improvement this paper and the provision of specialized software.

References

• Baesens, B., Van Gestel, T., Viaene, S., Stepanova, M., Suykens, J., & Vanthienen, J. (2003). Benchmarking state-of-the-art classification algorithms for credit scoring. Journal of the operational research society, 54(6), 627-635.
• Durand, D. (1941). Risk Elements in Consumer Installment Financing. National Bureau of Economic Research Books.
• Free Credit Reports (2017). Consumer Information. https://advocacy.consumerreports.org/
• Hand, D. J., & Henley W. E. (1997). Statistical Classification Methods in Consumer Credit Scoring: A Review. Journal of the Royal Statistical Society: Series A (Statistics in Society), 160(3), 523-541.
• Hens, A. B., & Tiwari, M. K. (2012). Computational time reduction for credit scoring: An integrated approach based on support vector machine and stratified sampling method. Expert Systems with Applications, 39(8), 6774-6781.
• How Borrowers Can Use TransUnion (2015). CreditVision to Get Better Loan Rates GOBankingRates. GOBankingRates. https://www.gobankingrates.com/credit/credit-score/transunions-creditvision-better-lending-rates/
• Hsu, C. W., & Lin, C. J. (2002). A comparison of methods for multiclass support vector machines. IEEE transactions on Neural Networks, 13(2), 415-425.
• Hu, Q., Che, X., & Zhang, L. (2012). Rank Entropy-Based Decision Trees for Monotonic Classification. IEEE Transactions on Knowledge and Data Engineering, 24(11), 2052-2064.
• Korneev, V. V., Gareev, A. F., Vasyutin, S. V., & Reich, V. V. (2001). Database. Intelligent information processing. Publishing house Nolidzh.
• Khemais, Z., Nesrine, D., & Mohamed, M. (2016). Credit Scoring and Default Risk Prediction: A Comparative Study between Discriminant Analysis & Logistic Regression. International Journal of Economics and Finance, 8(4), 39-53.
• Louzada, F., Anacleto-Junior, O., Candolo, C., & Mazucheli, J. (2011). Poly-bagging Predictors for Classification Modelling for Credit Scoring. Expert Systems with Applications, 38(10), 12717–12720.
• Lugger, G. F. (2004). Artificial Intelligence: Strategies and Methods for Solving Complex Problems. Williams Publishing House.
• Skupchenko A. V., & Semeykin V. D. (2009). Modelling of artificial neural networks in Matlab Environment. Vestnik of the Astrakhan State Technical University. Series: management, computer engineering and computer science, 1, 159-164.
• Vapnik, V. N. (1999). An Overview of Statistical Learning Theory. IEEE transactions on neural networks, 10(5), 988–999.
• Volkova, E. S., Gisin, V. B., & Solov'ev, V. I. (2017a). Data Mining Techniques: Modern Approaches to Application in Credit Scoring. Finance and Credit, 23(34), 2044-2060.
• Volkova, E. S., Gisin, V. B., & Solov'ev, V. I. (2017b). Methods of Fuzzy Set Theory in Credit Scoring. Finance and Credit. 23. (35). 2088-2106.
• Weston, J., Mukherjee, S., Chapelle, O., Pontil, M., Poggio, T., & Vapnik, V. (2000). Feature selection for SVMs. Advances in Neural Information Processing Systems, 13, 668-674.
• Yap, B. W., Ong, S. H., & Husain, N. H. M. (2011). Using Data Mining to Improve Assessment of Credit Worthiness via Credit Scoring Models. Expert Systems with Applications, 38(10), 13274-13283.