Abstract
Inter-sectoral balance models in the economy are widely used. One of the main tasks solved using input – output analysis is the estimation of the gross output vector. This task refers to inverse problems. Inverse problems with a large number of variables are often ill conditioned. Solving ill conditioned problems leads to large errors in the solution, even with small errors in the source data. In this regard, the task of finding the gross output vector from inaccurate data is relevant. The paper considers the task of estimating the parameters of the gross output vector in the presence of errors in the direct cost matrix and the final consumption vector. The use of the total least squares (TLS) method is proposed. TLS estimation of the gross output vector is obtained using an augmented system of equations of inter-sectoral balance, which is equivalent to a normal biased system of linear equations. Numbers of condition for a normal biased system of equations of inter-sectoral balance and an equivalent augmented system of equations of inter-sectoral balance are given. Tests showed that the accuracy of the proposed estimate of the gross output vector is higher than that of the estimate obtained using the least squares (LS) method.
Keywords: Input–output analysisinter-sectoral balancetotal least squareerrors-in-variablesill conditioning
Introduction
Inter-sectoral balance models in the economy are widely used (Leontief, 1986; Miller & Blair, 2009). Input–output analysis is the name given to an analytical framework developed by Professor Wassily Leontief in the late 1930s, in recognition of which he received the Nobel Prize in Economic Science in 1973. Input – output analysis applications are discussed in (Alabi, Munday, Swales, & Turner, 2019; Cassar & Rapa, 2018; Wang, Jiang, & Li, 2018, Richter, Mendis, Nies, & Sutherland, 2019). One of the main tasks solved using input – output analysis is the estimation of the gross output vector. This task refers to inverse problems. Inverse problems with a large number of variables are often ill-conditioned. Solving ill conditioned problems leads to big errors in the solution, even with small errors in the source data. In this regard, the task of finding the gross output vector from inaccurate data is relevant.
Problem Statement
The system of equations of inter-sectoral balance can be written in matrix form:
(1)
где
is gross output vector;
is vector of the final product;
is direct cost matrix.
Equation (1) is called the linear inter-sectoral balance equation.
The main task of the inter-sectoral balance is to find such a vector of gross output , which, given the known matrix of direct costs , provides a given vector of the final product .
We transform the equation (1)
,(2)
where is unit matrix of dimension .
If the matrix is singular, equation (2) has a unique solution
(3)
When solving real economic applications, the direct cost matrix, as well as the vector of the final product are unknown, and only their estimates are known. In addition, estimates of these parameters obtained by different calculation methods may vary. To estimate the gross output vector, it is necessary to solve an overdetermined system of linear equations with errors in the right and left parts.
It is required to find an approximate solution to the system
(4)
где ,
from approximate values
Research Questions
The paper is devoted to the estimation of the gross output vector of the inter-sectoral balance of a macroeconomic system. The issue of estimating the parameters of the gross output vector in the presence of errors in the direct cost matrix and the final consumption vector is considered. An estimate of the gross output vector based on an augmented system of equations, which is equivalent to a normal biased system of equations, is proposed.
Purpose of the Study
The purpose of the paper is to develop a methodology for estimating the gross output vector in the presence of errors in variables. The condition numbers for a normal bias system of inter-industry balance equations and an equivalent augmented system of inter-industry balance equations are given. Tests have shown that the accuracy of the proposed estimate of the gross output vector is higher than that obtained using the least squares method
Research Methods
Solving the problem of the total least squares method on the basis of a normal biased system of equations
Problem (4) can be solved by the total least squares method. The problem is reduced to finding a vector
(5)
There are several approaches to minimizing (5). The first approach is based on the fact that the solution of problem (2) requires calculating the minimum singular number of the extended matrix and the corresponding right singular vector corresponding to this number.
The problem of finding a singular vector is a nonlinear vector problem. Its numerical solution is associated with significant difficulties associated with the stability of search algorithms, convergence issues, and high computational complexity.
The second approach is based on solving a biased normal system. In (Zhdanov, 1988) it is shown that if the condition
(6)
The solution to problem (4) can be obtained from a biased normal system of equations
(7)
When solving system (7), only the scalar problem of finding the minimum singular number remains nonlinear
This task is always well-conditioned. The vector problem is linear. The system of linear algebraic equations (7) is always well-conditioned than the usual normal system. The condition number of the normal biased matrix is determined from the following relation:
(8)
Solving the problem of the total least-squares method using an augmented system of equations with complex coefficients
In (Zhdanov & Shamarov, 2000) it is proposed to use an augmented system equivalent to a biased normal system.
(9)
or
(10)
wherе is arbitrary positive factor,
- is imaginary unit , .
The condition number of the matrix has the form
(11)
where are maximum and minimum eigenvalues of the matrix
The problem of finding the minimum value of the condition number can be considered as the problem of choosing the optimal factor :
(12)
Problem (12) has no analytical solution, but can be solved by numerical methods. In practice, as an estimate, you can use
(13)
Problem (11) can be solved, for example, using the LU decomposition.
Findings
The gross output vector was estimated using 4 implementations of the system of equations (1) using the least squares method and the total least squares method based on the augmented system (11).
The values of the direct cost matrix are shown in Table
Errors in the input and output data were modeled by the addition of independent Gaussian distributed random variables . 50 simulations were performed.
Test cases were compared by the normalized root mean square error (NRMSE) of parameter estimation, defined as
The simulation results in Matlab are presented in Figure
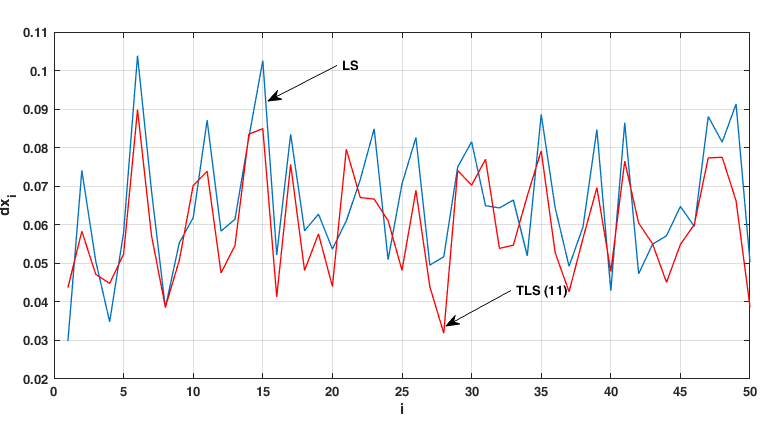
Source: authors.
Table
Condition numbers for a normal biased system (7) and for equivalent augmented system (11) are:
Conclusion
The paper proposes estimates the gross output vector based on the solution of the total least squares problem. The simulation results show that the augmented system has a lower number of conditionality than the bias normal system. The direction of further research will be a application of the results (Ivanov & Ivanov, 2017; Ivanov, Sandler & Kozlov, 2018) for estimation of the gross output vector of the Leontief dynamic model and the fractional order Leontief model.
Acknowledgments
The authors gratefully acknowledge the contributions of prof. O. A. Katsyuba in improving the paper.
References
- Alabi, O., Munday, M., Swales, K., & Turner, K. (2019). Physical water use and water sector activity in environmental input-output analysis. The Review of Regional Studies, 49(2), 268-291.
- Cassar, I. P., & Rapa, N. (2018). Estimates of input-output multipliers for the Maltese economy based on the symmetric input-output table for 2010. Xjenza, 6(2), 70-85. DOI: 10.7423/XJENZA.2018.2.01
- Ivanov, D. V., & Ivanov, A. V. (2017). Identification fractional linear dynamic systems with fractional errors-in-variables. Journal of Physics: Conference Series, 803(1), 012058. DOI: 10.1088/1742-6596/803/1/012058
- Ivanov, D. V., Sandler, I. L., & Kozlov, E. V. (2018). Identification of fractional linear dynamical systems with autocorrelated errors in variables by generalized instrumental variables. IFAC-PapersOnLine, 51(32), 580-584.
- Ke, W., Sha, J., Yan, J., Zhang, G., & Wu, R. (2016). A multi-objective input–output linear model for water supply, economic growth and environmental planning in resource-based cities. Sustainability, 8(2), 160. DOI: 10.3390/su8020160.
- Leontief, W. (1986). Input-output economics. New York: Oxford University Press.
- Miller, R. E., & Blair, P. D. (2009). Input-output analysis: Foundations and extensions. Cambridge: Cambridge University Press.
- Richter, J. S., Mendis, G. P., Nies, L., & Sutherland, J. W. (2019). A method for economic input-output social impact analysis with application to U.S. advanced manufacturing, Journal of Cleaner Production, 212, 302-312.
- Wang, O., Jiang, R., & Li, R. (2018). Decoupling analysis of economic growth from water use in city: A case study of Beijing, Shanghai, and Guangzhou of China. Sustainable Cities and Society, 41, 86-94.
- Zhdanov, A. I., & Shamarov, P. A. (2000). A direct projection method in the problem of complete least squares. Autom. Remote Control, 61(4), 610–620.
- Zhdanov, A. I. (1988). The solution of ill-posed stochastic linear algebraic equations by the maximum likelihood regularization method. USSR Computational Mathematics and Mathematical Physics, 28(5), 93-96.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
01 April 2020
Article Doi
eBook ISBN
978-1-80296-081-5
Publisher
European Publisher
Volume
82
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-1004
Subjects
Business, innovation, management, management techniques, development studies
Cite this article as:
Ivanov, D. V. (2020). Estimation Of The Gross Output Vector Of Inter-Sectoral Balance Of Macroeconomic System. In V. V. Mantulenko (Ed.), Problems of Enterprise Development: Theory and Practice, vol 82. European Proceedings of Social and Behavioural Sciences (pp. 672-678). European Publisher. https://doi.org/10.15405/epsbs.2020.04.85
