Comparison Of Stratified And Random Iterative Sampling In Evaluation Of Pls-Da Model

Loong Chuen Lee

Abstract

Model evaluation is used to derive model performance index that indicates practical values of prediction model. In practice, it occurs in the last step of the statistical modelling pipeline; and various types of model evaluation methods or strategies have been proposed in the literature. Iterative resampling strategy is believed to be more reliable than sampling approach like Kennard-stone algorithm because it produces more than one test set to ensure better representativeness. Most of the iterative resampling methods available in commercial statistical software implement random resampling by default. This would produce biased estimator if the studied dataset is imbalanced, i.e . unequal group sizes. As a result, stratified resampling has been proposed to ensure similar class proportions in both the test and training sets. This preliminary work aims to explore empirical differences between stratified and random iterative sampling strategies in assessing performances of partial least squares-discriminant analysis (PLS-DA) model using imbalanced attenuated total reflectance-Fourier transform infrared (ATR-FTIR) spectra of blue gel pen inks. The dataset consisted of 1361 spectra and 5401 variables; and can be classified into ten different pen brands ( i.e . groups). The findings demonstrate the merit and pitfalls of the two resampling strategies.

Keywords: ATR-FTIR spectrumpartial least squares-discriminant analysis (PLS-DA)model validationforensic science

Introduction

Model evaluation is an important aspect along the statistical modelling pipeline, especially in the context of chemometrics. This is because it enables researchers to gain more insight about the potential of the prediction model in real-world settings. In fact, a wealth of model evaluation methods have been described in the literature ( Colins et al., 2014). Each is characterized by unique merits and pitfalls. Internal validation methods including v -fold cross validation and auto-prediction are easy to be conducted and economic because require no new samples. However, both approaches are often claimed to be less objective than external validation, especially the latter tends to present over-optimistic estimates ( Refaeilzadeh, Tang, & Liu, 2009; Hawkins, 2004). On the other hand, external testing sample part of the dataset to be test samples which are not included in the model training. This ensure less risk of overfitting of the model ( Consonni, Ballabio, & Todeschini, 2010).

Recently, Lee, Liong, and Jemain ( 2018a) demonstrated the limitation of Kennard-stone sampling algorithm against the iterative random resampling approaches to derive model performance index via external testing method. On the other hand, Molinaro, Simon, and Pfeiffer ( 2005) reported comparative performances between different resampling methods, including v -fold cross validation, leave-one-out cross validation (LOOCV), Monte Carlo cross-validation (MCCV) and .632+Bootstrap methods. Both simulated and real microarray datasets with a range of sample sizes ( n = 40,80 a n d 120 ) were modelled using classification methods, i.e . linear discriminant analysis, Classification and Regression Trees and Neural Networks. Based on their findings, the resampling strategies show similar performances when the sample size is sufficiently big. In order to reduce bias caused by unequal group sizes, Molinaro et al. ( 2005) have used stratified resampling approaches in all the model validation methods.

Problem Statement

In practice, resampling strategies can be implemented randomly or systematically. The former allows the same sample to be resampled without restriction. It allows more possible number of combinations than the latter because systematic resampling ensures each sample only assigned as test set once. Random resampling is easy to run but could produce biased estimate if the dataset is imbalanced, i.e . varying group sizes. As a result, stratified resampling which samples test set by group was proposed. Stratified random resampling performs random resampling only on samples from the predefined group rather than on the whole samples. As such, stratified random resampling preserves similar class proportions in the training and corresponding test sets ( Molinaro et al., 2005). Kohavi ( 1995) has discussed the advantages of stratified resampling over random resampling in classification modelling by using cross-validation method.

Research Questions

This work aims to find answer for two different but related research questions:

What is the difference between stratified random iterative sampling (RIS) and stratified iterative sampling (SIS) in external testing method?

Does the relative difference between stratified and random resampling strategies affected by the number of iterations and PLS components?

Purpose of the Study

The purpose of this work is to examine merits and pitfalls of stratified (SIS) and random (RIS) resampling in external testing method. The PLS-DA technique and ATR-FTIR spectrum were used to construct the prediction models.

Research Methods

All statistical analysis was performed using the R environment for statistical computing and graphics, version 3.5.0 ( R Core Team 2018). PLS-DA was performed with ‘caret’ package ( Kuhn, 2019) and AsLS via ‘baseline’ package ( Liland & Mevik, 2015).

ATR-FTIR Spectral Dataset

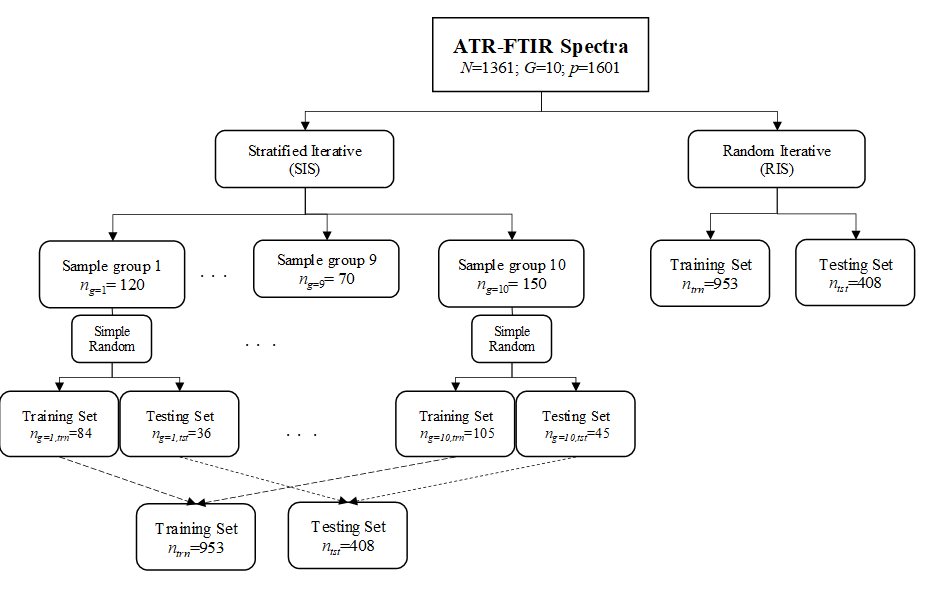
The primary spectral dataset consisting of 1361 samples and 5401 variables has been studied and reported elsewhere (Lee, Liong, & Jemain, 2018b, 2018c, 2019a, 2019b). The practical purpose of classification model is to predict brand of unknown pen inks using based on ATR-FTIR spectrum of the ink entry. Table 01 shows the number of spectrum according to ten different pen brands. More details about the spectra collection procedures can be referred to Lee, Liong, and Jemain ( 2018b). The dataset was first truncated and included only region between 2000-1600 cm -1; and then preprocessed using Asymmetric Least Squares (AsLS) algorithm ( Eilers & Boelens, 2005). The pretreatment procedures are in accordance with the previous works conducted using the same spectral dataset ( Lee, Liong, & Jemain, 2018c).

Table 1 -
See Full Size >

Partial Least Squares-Discriminant Analysis (PLS-DA) Method

The dataset was split into 7:3 training and test sets using stratified (SIS) and random (RIS) iterative sampling strategies. Both strategies were repeated for r = 1,2 , . . . , 1000 times to draw a total of 408 test samples from the primary spectral dataset. Figure 01 illustrates the technical differences between the two resampling strategies in sampling 408 spectra for external testing purpose. External prediction accuracy (Acc) was computed using the test sets as follows:

A c c = n t s t ' n t s t

where n t s t and n t s t ' respectively denote total number of test set and correctly predicted test samples, n t s t ' ≤ n t s t .

Model Validation

The dataset was split into 7:3 training and test sets using stratified (SIS) and random (RIS) iterative sampling strategies. Both strategies were repeated for r = 1,2 , . . . , 1000 times to draw a total of 408 test samples from the primary spectral dataset. Figure 01 illustrates the technical differences between the two resampling strategies in sampling 408 spectra for external testing purpose. External prediction accuracy (Acc) was computed using the test sets as follows:

A c c = n t s t ' n t s t

where n t s t and n t s t ' respectively denote total number of test set and correctly predicted test samples, n t s t ' ≤ n t s t .

Figure 1: General procedures used in simple random and stratified random sampling. The procedures are repeated for r times.
General procedures used in simple random and stratified random sampling. The procedures are repeated for r times.
See Full Size >

Comparison Analysis

The two resampling strategies were compared using descriptive and inferential statistics as well as exploratory tool, i.e. principal component analysis (PCA). The list of accuracy rates were used to compute mean ( x - ) , standard deviations (SD) and coefficient of variation (CV) as shown below:

x - = 1 n r ∑ i = 1 n r x i S D = ∑ i = 1 n r ( x i - x - ) 2 n r - 1 C V = S D x -

where x denotes accuracy rates and n r refers to the number of iterations. Two-tailed hypothesis tests, i.e. paired t -test and Wilcoxon signed rank test, were also employed to asses if the difference observed in terms of model accuracy is significant at 5% level of significance. Last but not least, PCA was conducted to illustrate spatial distribution of the two resampling strategies in different perspectives ( Bro & Smilde, 2014). Scores plot of the first two principal components shows the relative distances between RIR and SIR.

Findings

The performances of RIS and SIS were compared sequentially via descriptive and inferential statistics. In order to gain more comprehensive insights, the difference has been assessed by considering the impacts of number of PLS components and iterations. Table 02 shows the mean and CV values of RIS and SIS by number of PLS components and iterations. It clearly shows that RIS and SIS exhibit similar performances when involves more number of PLS components or number of iterations increases. Model series that constructed using the first 10 PLS components tend to present pessimistic accuracy rates with RIS approach. However, both RIS and SIS produced similar accuracy rates as the number of iterations increased or after includes more number of PLS components. This is supported by the p -values estimating via paired t -test or Wilcoxon rank-signed test as summarized in Table 02 .

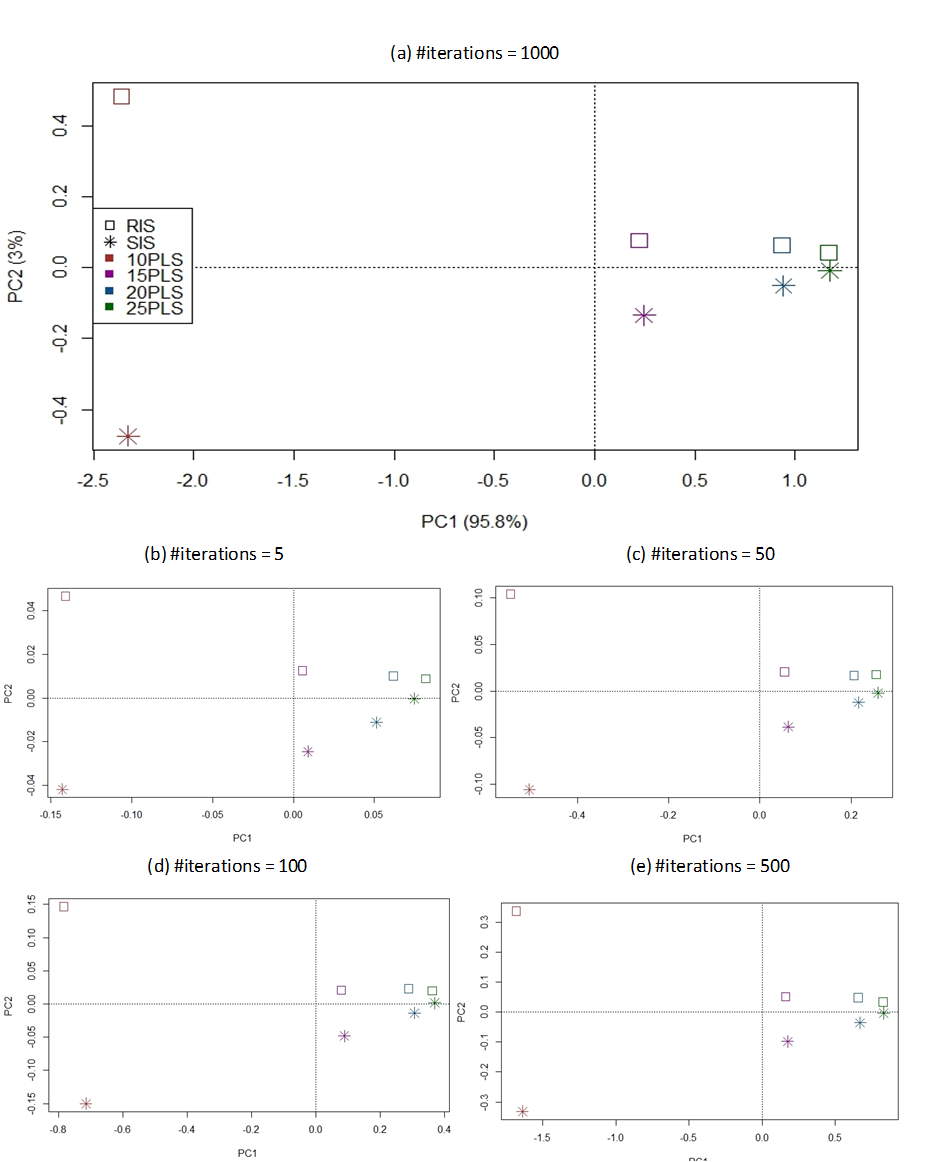
In addition, the respective CV values reduce as the model includes more number of PLS components. It can be clearly seen from Table 02 , degree of changes of CV values along different number of iterations highly depends on the number of PLS components. As more number of PLS components have been included in the model, number of iterations causes insignificant changes in the CV values. Contrarily, changes of CV values can be drastic in models including only the first 10 PLS components. Results deriving from the descriptive statistics are confirmed by the respective inferential statistics. This is because none of p -values presented in Table 03 is less than 0.05.

Figure 02 shows the relative distances between RIS and SIS using scores plot of PCA. It is clearly demonstrated that both RIS and SIS become similar to each other when more number of PLS components were included in the model. In addition, it is important to note that the trend of relationship between the two strategies is unlikely being affected by the number of iterations. The overall patterns projected by the two resampling strategies over the four different number of PLS components are preserved regardless of the number of iterations being considered.

In other words, this indicates both RIS and SIS are quite similar in performances. This provides evidence to state that stratification is not necessary in validating a colossal, multi-class and imbalanced spectral dataset. However, this is not in line with previous work stated stratified sampling shall be preferred in imbalanced dataset ( Kohavi, 1995). Such discrepancy can be partly explained by the fact that the studied dataset is of colossal size; and each group has been represented by rather large sample size. As a result, the relative class proportions show less deviations between the different drawn even simple random techniques has been adopted.

Table 2 -
See Full Size >
Table 3 -
See Full Size >
Figure 2: Scores plots show distribution among the two resampling strategies across different number of PLS components by considering different number of iterations
Scores plots show distribution among the two resampling strategies across different number of PLS components by considering different number of iterations
See Full Size >

Conclusion

This work has compared empirical performances between random (RIS) and stratified (SIS) iterative sampling methods in PLS-DA model. It is concluded that simple random resampling can be as reliable as stratified resampling in deriving model performance using imbalanced dataset if the dataset is of colossal size.

Acknowledgments

This work was supported by the CRIM, UKM (GUP-2017-043).

References

Copyright information

Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

About this article

Publication Date

30 March 2020

Article Doi

https://doi.org/10.15405/epsbs.2020.03.03.75

eBook ISBN

978-1-80296-080-8

Publisher

European Publisher

Volume

81

Print ISBN (optional)

-

Edition Number

1st Edition

Pages

1-839

Subjects

Business, innovation, sustainability, development studies

Cite this article as:

Lee, L. C. (2020). Comparison Of Stratified And Random Iterative Sampling In Evaluation Of Pls-Da Model. In N. Baba Rahim (Ed.), Multidisciplinary Research as Agent of Change for Industrial Revolution 4.0, vol 81. European Proceedings of Social and Behavioural Sciences (pp. 648-656). European Publisher. https://doi.org/10.15405/epsbs.2020.03.03.75

Copy citation text