Impact Of Learning Strategies Instruction On Students’ Mathematical Texts Comprehension Performance

Abstract

Negative attitudes towards mathematics appear early and correlate with difficulties to comprehend tasks. Can the learning strategies instruction help students to develop better skills for comprehending mathematical texts? The research question was to define the extent of the impact of the instruction of learning strategies on the performance of the third grade primary school students who were taught mathematical texts’ comprehension. The purpose of this article was to establish the influence of the instruction of learning strategies on mathematical texts’ comprehension of the third grade primary school students. The results whether two factors – students’ cognitive abilities and their socio-economic status affected the performance of the mathematical texts’ comprehension. An experimental project with pre-test and post-test measurements was created. The experimental group consisted of 46 girls and boys, and the control group consisted of 59 girls and boys (9–10 years). The data analysis methods were descriptive, probability and multidimensional statistics. Statistically significant differences were not found in the analysis of average mathematical texts comprehension performance in the experimental group in comparison to control group ( p  < 0,05). The results of study revealed that purposeful teaching of students to apply a learning strategy is a factor that has very small effect. The mathematical literacy previously acquired by the students, their learning achievements are much more influential factors for the students' further progress. Those with higher achievements continue to progress, those with lower achievements lag behind.

Keywords: Learning strategies’ instructionmathematical texts comprehension

Introduction

In elementary school, children are provided with basic knowledge, which is crucial for their further achievement. The development of mathematical literacy skills is one of the main educational objectives of the European Union. Education documents in the European Union emphasize the importance of developing mathematical literacy skills as a key factor in the success of school education and in people's lives. The results of the TIMSS study indicate that a relatively small proportion of Lithuanian fourth-graders reach the highest international level of mathematics achievement (TIMSS Report, 2015). According to the results of standardized tests of Lithuanian fourth-grade students, until 2017 relatively good progress has been made in this area, reading is still one of the most problematic areas of primary education in Lithuania (NEC, 2017).

Negative attitudes towards mathematics appear early and correlate with difficulties to comprehend tasks. Mathematical text comprehension is related with reading comprehension and mathematics word problems as well. Mathematics word problems (further MWP) require the transfer of knowledge to novel situations, and this form of transfer can be difficult to effect especially for primary-grade children (Fuchs et. al., 2008).

Reading comprehension is a multifaceted and complex ability where multiple reading subsets and cognitive processes work together, such as: visual attention, processing speed, verbal decoding, lexical search, syntactic and contextual integration (Meixner, Warner, Lensing, Schiefele, & Elsner, 2019). Interactions between these subgroups require higher-level cognitive abilities, such as focusing, targeting, and suppressing inappropriate information. Recent research in neuroscience contributes to knowing how a person reads, what processes occur in the brain during reading. The ability to understand informational text is thought to rely on processes that help the reader create a consistent and accurate representation of the text, and processing speed, vocabulary, fluency, and decoding skills (e.g. Cutting, Materek, Cole, Levine, & Mahone. 2009). For successful comprehension, readers have to meaningfully integrate information into sentences in order to achieve a generally recognized level of text comprehension. As readers engage with the text, learning occurs by drawing conclusions and modifying readers' existing knowledge by adapting new concepts introduced in the text (Hooper, Rose, & Sperling, 2018). Therefore, recent studies have highlighted the influence of brain executive functions on the development of reading comprehension, particularly in the context of preschool and elementary education (Meixner et al., 2019).

The influence of learning strategies on the achievement of students of all ages is increasingly attracting the attention of researchers. Oxford has been the most consistent researcher on learning strategies for several decades and has provided a classification and concept of learning strategies (Oxford, 2016). Learning strategies were explored through the analysis aspects of foreign language learning. Self-management and motivation (e.g. Gerami & Baighlou, 2011; Rose, Briggs, Boggs, Sergio, & Ivanova-Slavianskaia, 2018; Lin, Zhang, & Zheng, 2017), the ability of students in grades 5-7 to apply learning strategies in mathematics lessons (Pennequin, Sorel, Nanty, & Fontaine, 2010; Sičiūnienė, 2015). Recently researchers analysed the development of reading skills through reading strategies (Säälik, Nissinen, & Malin 2015; Toleikytė, 2014; Sičiūnienė & Toleikytė, 2017) and the application of meta-cognitive learning strategies (e.g. Veselinov & Nikolic, 2015). Baten, Praet and Desoete (2017) state that a meta-cognitive training model plays an important role to stimulate the development of reading skills in early childhood. Experiments have proven that reading strategies can improve the ability to understand the text being read (Toleikytė, 2014). Readers with good reading skills often find effective reading strategies themselves, can apply them consciously and unconsciously, but students with reading difficulties are unable to read strategically, and if they are not taught effective reading strategies in the teaching process, there is no way to bridge the gap between them and the strongest students (Faggella-Luby, Deshler, 2008; Li, Beecher, & Cho, 2018).

Teaching practices are the most significant factors in explaining students’ academic outcomes (Caro, Lenkeit, & Kyriakides, 2016; Egloff, Förster, & Souvignier, 2019). Fuchs et al. (2008) revealed that the tutored students who received validated classroom instruction achieved better than the tutored students who received conventional classroom instruction. Tutoring, not validated classroom instruction reduced the prevalence of math difficulty. According to Raižienė, Stumbrienė, Ringienė, Dukynaitė and Jakaitienė (2019), the adaption of instruction significantly contributes to students’ performance in all EU education systems. Students’ need for competence is satisfied when teachers are perceived as adapting their instructions to students’ diverse experience and cognitive preferences (Lau & Lam, 2017; Raižienė et al., 2019). The results of Raižienė et al. (2019) study reveal that students in all EU countries would benefit from adaptive instruction. The adaption of instruction is positively related and perceived feedback is negatively related to science performance. These patterns of associations are similar across all observed EU countries. Adaption of instruction refers to teachers’ flexibility in constructing the lessons (OECD, 2016). Caro et al. (2016) findings show, that association between students’ oriented learning strategies and mathematics performance are inconsistent across education systems according to 2012 year data from Programme for International Student Assessment .

Baten et al. (2017) propose to reinforce the meta-cognitive knowledge and skills of primary school students through modelling, pedagogical support, reflection, feedback, assessments, advice to the learner and observation. It is important to apply strategies that encompass a variety of thinking processes: cognitive, socio-emotional, and meta-cognitive (Toleikytė, 2014). Researchers stress that learning to read and learning other strategies should be systematic, coherent and challenging for students process, i.e. gradual transition from guided to autonomous learning, gradually increasing the degree of learning autonomy (Gibson, 2008, Tracy, Reid, & Graham, 2009; Toleikytė, 2014; Sičiūnienė & Toleikytė, 2017; De Smedt & Van Keer, 2018).

However, while research on the application of learning strategies is abundant and research has shown that learning strategies influence reading comprehension (Muijselaar et al., 2017), researchers note that their outcomes are not always transferable and adaptable to educational decisions (Chou, 2013). VanDerHeyden and Witt (2005) identified that nine practice sessions with feedback and reinforcement increase basic fact fluency. According to the other study, tutoring, not validated classroom instruction, and reduced the prevalence of math difficulty (Fuchs et al., 2008). The majority of teachers do not use a carefully planned training material in the classroom (Chou, 2013; Star, Rittle-Johnson, & Durkin, 2016; De Smedt & Van Keer, 2018). Thus, teachers need didactic recommendations which, how and when the recommended training tools to use, that the learning strategies would become an inseparable part of the lesson. Raižienė et al (2019) estimated the positive statistically significant links between teacher support and science performance in 8 countries (Finland, Estonia, Lithuania, Sweden, UK, Latvia, Denmark, and Hungary).

Learning strategies in this study are explored using a constructivist learning model (Hattie, Donoghue, 2016), which consists of the following components: three sets of learning outcomes and three kinds of achievements, i.e. students' understanding of the criteria for success in the task, three stages of the learning process (superficial, deep and transferable learning), where superficial and deep learning involve each stage of knowledge acquisition and consolidation and the connecting component is the learning environment. As the teacher plays an important role in teaching learning strategies, the work is based on the model of teaching learning strategies and (according to Gibson, 2008, Tracy et al., 2009, De Smedt & Van Keer, 2018) it is emphasized that teacher mastery determines the correct application of strategy.

Problem Statement

Negative attitudes towards mathematics appear early and correlate with difficulties to comprehend tasks. There is still a lack of research analysing the influence of learning strategies on the development of reading information texts in primary school. Analysing non-fiction text comprehension teaching in primary school and reader development strategies in Lithuanian textbooks (Salienė, 2010) it was found that not all Lithuanian textbooks have enough tasks related to reading a non-fiction text. There is a lack of research on how a teacher should teach learning strategies in lessons so that they can be effectively applied and students can discover them independently in the learning tools. Can the learning strategies instruction help students to develop better skills for comprehending mathematical texts?

Research Questions

There are the following research questions: 1. How does the instruction of learning strategies affect the performance of the primary school students’ mathematical texts comprehension? 2. To what extent are students’ cognitive skills developed applying learning strategies?

Purpose of the Study

The purpose of the present study, therefore, was to establish the efficiency of the instruction of learning strategies on mathematical texts’ comprehension of the third grade primary school students’ and to find out whether two factors – students’ cognitive abilities and their socio-economic status affect the performance of the mathematical texts’ comprehension.

Research Methods

Findings

The difference between the pre- and post-test averages for the entire study sample (n₁) when comparing the intervention section and the comparison section indicates greater progress in the intervention section. However, the calculated effect size using a psychometric calculator shows that purposeful teaching of students to apply a learning strategy had virtually no effect. Next, a group of students was identified for whom the instruction and work with the learning strategy action algorithm might have influenced their progress. First of all, students who received the maximum possible assessment in the pre-test were eliminated from the entire sample. Next, the results of the Lucid Recall , GB test were used to eliminate a portion of the sample that was significantly distant from the typical cognitive abilities estimation (i.e., students with individual educational needs) and to form a redesigned study group - n₂. In this precise group, the effect size is weak but can be interpreted. In this group, the difference between the pre- and post-measurement averages indicates greater student progress in the intervention section.

When it was found that the teaching of students to apply strategy in solving mathematics word problems had a weak effect, factors that are more powerful were searched. Multiple linear regression analysis and correlation were applied to determine which factors influenced the progress of student achievement (see Table 02 ).

The results of multiple linear regression analysis and correlation confirm that purposeful teaching of students to apply a learning strategy is a factor that has very little effect. The mathematical literacy already acquired by the students, their learning achievements and their compliance with the typical assessment of cognitive abilities are much more influential.

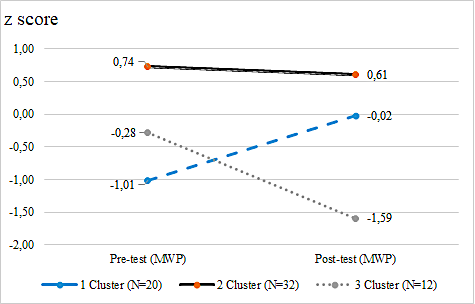
K-means cluster analysis conducted to identify groupings of sample based on their pre-test and post-test results. The division of the respondent into three clusters is the most informative according to the dynamics (see Figure 01 ). The differences among groups (clusters) are statistically significant (ANOVA test, p = 0,000). Every cluster represents a group of students with its particular and different learning experience and changes during the period of the experiment. The whole sample was divided into clusters not differentiating into control or experimental groups (N=90; 26 cases (30 percent) were not involved). The differences among the determined types of students are contrasting enough.

Cluster 1 (N = 20 (22%; N_I: 13%; N_C: 9%) includes students with the lowest pre-test scores in the sample, but post-test scores show progress. Cluster 2 (N = 32 (36%; N_I: 18%; N_C: 18%)) includes students with relatively high pre-test scores but 6 months later progress has not been demonstrated.

Cluster 3 (N = 12 (22%; N_I: 8%; N_C: 6%)) includes students with lower post-test scores than pre-test ones. The even distribution of students from the intervention (N_I) and control (N_C) groups into clusters indicates that the presence or absence of progress cannot be directly attributed to the teaching of learning strategies or to the preparation of students to apply a strategy in solving mathematics word problems. This correlates with the results of regression analysis, which also showed that the learner's numeracy and correspondence with a typical level of cognitive ability had a strong influence on further learning.

Pennequin et al. (2010), Cornoldi, Carretti, Drusi and Tencati (2015) indicate that teaching metacognitive strategies is particularly influential to less successful students. Weaker learners acquire more motivation to perceive the text better when a collaborative teaching and learning method is applied. Teaching reading strategies this way another important aspect of strategy teaching will be provided – a complex solution of the problems of reading motivation (Sičiūnienė & Toleikytė, 2017).

See Full Size >

Researchers of this study agree with other studies findings (i.e. Star et al., 2016; Durkin, Star, & Rittle-Johnson, 2017), that the fact that study did not show significant improvement in student achievement shows that teachers need more didactic guidance. It is useful teaching students to solve math word problems strategies to compare multidimensional strategies. Next decision for our research would be to include into educational intervention such steps:

(a) Regular and frequent comparisons of alternative strategies, in particular after some time when students succeeded in smoothly applying one initial strategy;

(b) Conscious choice of strategies and problems to compare;

(c) Carefully designed the visual presentation of multidimensional strategies;

(d) Using small group and whole class discussions to compare multiple strategies, focusing on approach similarities, differences, accessibility and limitations (Durkin et al, 2017, p. 594).

Baten et al. (2017) state that meta-cognitive training stimulates children's early mathematical abilities. It considerably depends on the presentation of strategies, practical training in their application and constant discussion. In addition, the meta-cognitive knowledge and skills of primary school students should be enhanced through modelling, pedagogical support, reflection, suitable for the student feedback, assessments, advice and observation. Learning should progressively shift from guided to independent reading, increasing the degree of learning autonomy (Fuchs, et al., 2008; Sičiūnienė & Toleikytė, 2017).

This work has several limitations that are important to consider when interpreting the results. The fact that a teacher in one experimental class was a beginner and had less experience than an experienced educator in another might have influenced the results of the experiment. Experienced teachers are different from beginners (Auerbach, Higgins, Brickman, & Andrews, 2018): experts are more likely to focus on student assessment and responsibility teaching, the students' difficulties with the subject matter, notice how students are asked to explain their understanding, how a teacher responds into students' reflections, on the scope for students to work independently and develop their own ideas.

Conclusion

The results of the study revealed that purposeful teaching of students to apply a learning strategy is a factor that has very small effect. From the current study, we conclude that the different learning experiences and achievements of the students strongly influence the students' further progress. Those with higher achievements continue to progress, those with lower achievements lag behind. The research findings highlighted a group of students who, having mastered a typical learning strategy for solving a particular learning problem and / or to do a learning activity continued to do so independently and made progress.

The results of the research revealed three meaningful sample groups (clusters), which connect students with different learning experiences, achievements and learning opportunities. Each of these groups requires different teacher support, attention, and effort. A group that outperforms the sample, masters learning strategies faster, and is very likely to learn the strategies independently. This group requires more complex tasks and fewer typical tasks. That group does not add value to typical solution instructions and iterations. A group has emerged that needs more teacher support in learning and developing independent learning skills. This is the group that is harder to generate the possible solution on its own, the group that needs the coaching phase, for which it is very important to show the sequence of the learning strategy and monitor it until the learning strategy becomes a routine. This group, once mastered in learning strategies, is expected to achieve better learning results. The group that joins the smallest cluster is the group that needs the most pedagogical mastery and differentiated access. This group needs to be given extra time and individualized tasks to 'lead' it out of the wrong learning set and to progress.

Acknowledgments

The study is part of the project partially funded by Lithuania Agency for Science, Innovation and Technology and Publishing House and Training Centre “Šviesa“, according to contract No. 01.2.1-MITA-K-824-01-0117.

References

1. Auerbach, A. J., Higgins, M., Brickman, P., & Andrews, T. C. (2018). Teacher Knowledge for Active-Learning Instruction: Expert-Novice Comparison Reveals Differences. CBE—Life Sciences Education, 17(1), ar12.
2. Baten, E., Praet, M., & Desoete, A. (2017). The Relevance and Efficacy of Metacognition for Instructional Design in the Domain of Mathematics. ZDM Mathematics Education, 49(4), 613–623.
3. Caro, D. H., Lenkeit, J., & Kyriakides, L. (2016). Teaching strategies and differential effectiveness across learning contexts: Evidence from PISA 2012. Studies in Educational Evaluation, 49, 30–41.
4. Chou, M. H. (2013). Strategy use for reading English for general and specific academic purposes in testing and nontesting contexts. Reading Research Quarterly, 48(2), 175–197.
5. Clair-Thompson, H. S. (2015). Lucid Recall Administrator's Manual.
6. Cornoldi, C., Carretti, B., Drusi, S., & Tencati, C. (2015). Improving problem solving in primary school students: The effect of a training programme focusing on metacognition and working memory. British Journal of Educational Psychology, 85(3), 424-439.
7. Cutting, L. E., Materek, A., Cole, C. A., Levine, T. M., & Mahone, E. M. (2009). Effects of fluency, oral language, and executive function on reading comprehension performance. Annals of dyslexia, 59(1), 34-54.
8. Dehaene, S., & Cohen, L. (1997). Cerebral Pathways for Calculation: Double Dissociation between Rote Verbal and Quantitative Knowledge of Arithmetic. Cortex, 33, 219–250.
9. Durkin, K., Star, J. R., & Rittle-Johnson, B. (2017). Using Comparison of Multiple Strategies in the Mathematics Classroom: Lessons Learned and Next Steps. ZDM: The International Journal on Mathematics Education, 49(4), 585–597.
10. Egloff, F., Förster, N., & Souvignier, E. (2019). Students' Reading Ability Moderates the Effects of Teachers' Beliefs on Students' Reading Progress. Frontline Learning Research, 7(1), 1–22.
11. Faggella‐Luby, M. N., & Deshler, D. D. (2008). Reading comprehension in adolescents with LD: What we know; what we need to learn. Learning Disabilities Research & Practice, 23(2), 70–78.
12. Fuchs, L. S., Fuchs, D., Craddock, C., Hollenbeck, K. N., Hamlett, C. L., & Schatschneider, C. (2008). Effects of small-group tutoring with and without validated classroom instruction on at-risk students' math problem solving: are two tiers of prevention better than one? Journal of Educational Psychology, 100(3), 491–509.
13. Gaižauskaitė, I., & Valavičienė, N. (2016). Socialinių tyrimų metodai: kokybinis interviu: vadovėlis [Social Research Methods: Qualitative Interview: Textbook]. Valstybes Įmonė Registrų centras.
14. Gerami, M. H., & Baighlou, S. M. G. (2011). Language learning strategies used by successful and unsuccessful Iranian EFL students. Procedia-Social and Behavioral Sciences, 29, 1567–1576.
15. Gibson, S. A. (2008). Guided Writing Lessons: Second-Grade Students’ Development of Strategic Behavior. Reading Horizons: A Journal of Literacy and Language Arts, 48(2), 111–132. Retrieved from https://scholarworks.wmich.edu/reading_horizons/vol48/iss2/5
16. Gintilienė, G., & Butkienė, D. (2005). Raveno spalvotų progresuojančių matricų standartizacija Lietuvoje. Psychology, 32, 22–34.
17. Graß, K. H., & Krammer, G. (2018). Direct and Indirect Influences of Spatial Abilities on Mental Arithmetic Performance at the End of Primary School. Journal fur Mathematik-Didaktik, 39(1), 43-67.
18. Hattie, J. A., & Donoghue, G. M. (2016). Learning Strategies: a Synthesis and Conceptual Model. npj Science of Learning, 1(16013), 1–13.
19. Hooper, S., Rose, S., & Sperling, R. (2018, March). Using data to support instructional decision making: Designing a progress monitoring system to use with students who are Deaf or Hard of Hearing. In Society for Information Technology & Teacher Education International Conference (pp. 1503–1510). Association for the Advancement of Computing in Education (AACE).
20. Kardelis, K. (2007). Mokslinių tyrimų metodai ir metodologija. Šiauliai: Liucilijus.
21. Lau, K. C., & Lam, T. Y. P. (2017). Instructional Practices and Science Performance of 10 Top-performing Regions in PISA 2015. International Journal of Science Education, 39(15), 2128–2149.
22. Li, D., Beecher, C., & Cho, B. Y. (2018). Examining the Reading of Informational Text in 4th Grade Class and Its Relation with Students' Reading Performance. Reading Psychology, 39(1), 1–28.
23. Lin, C.-H., Zhang, Y., & Zheng, B. (2017). The Roles of learning Strategies and Motivation in Online Language Learning: A Structural Equation Modelling Analysis. Computers & Education, 113, 75–85.
24. Meixner, J. M., Warner, G. J., Lensing, N., Schiefele, U., & Elsner, B. (2019). The Relation between Executive Functions and Reading Comprehension in Primary-School Students: A Cross-Lagged-Panel Analysis. Early Childhood Research Quarterly, 46, 62–74.
25. Muijselaar, M. M. L., Swart, N. M., Steenbeek-Planting, E. G., Droop, M., Verhoeven, L., & de Jong, P. F. (2017). Developmental Relations between Reading Comprehension and Reading Strategies. Scientific Studies of Reading, 21(3), 194–209.
26. OECD (2016). PISA 2015 results (volume II): Policies and Practices for Successful Schools, PISA. Paris: OECD Publishing.
27. Oxford, R. L. (2016). Teaching and Researching Language Learning Strategies: Self-regulation in Context. Routledge.
28. Pennequin, V., Sorel, O., Nanty, I., & Fontaine, R. (2010). Metacognition and low achievement in mathematics: the effect of training in the use of metacognitive skills. Thinking and Reasoning, 16, 198–220.
29. Raižienė, S., Stumbrienė, D., Ringienė, L., Dukynaitė, R., & Jakaitienė, A. (2019). Students’ Performance and Teaching Practices in Science Across EU Countries: Evidence From Pisa 2015. The European Proceedings of Social & Behavioural Sciences, 53, 241–254.
30. Rose, H., Briggs, J. G., Boggs, J. A., Sergio, L., & Ivanova-Slavianskaia, N. (2018). A Systematic Review of Language Learner Strategy Research in the Face of Self-Regulation. System, 72, 151–163.
31. Rupšienė, L., & Rutkienė, A. (2016). Edukacinis eksperimentas: vadovėlis [Educational Experiment: A Textbook.] Klaipėda: Klaipėdos universiteto leidykla.
32. Säälik, Ü., Nissinen, K., & Malin, A. (2015). Learning strategies explaining differences in reading proficiency. Findings of Nordic and Baltic countries in PISA 2009. Learning and Individual Differences, 42, 36–43.
33. Salienė, V. (2010). Teksto rašymo mokymas pagrindinėje mokykloje: teorinės prielaidos ir praktinės galimybės. Pedagogika, 99, 71–76.
34. Sičiūnienė, V. (2015). Didaktiniai matematinio teksto skaitymo aspektai [Didactic Aspects of Reading Mathematical Text. Lithuanian Mathematical Collection] Lietuvos matematikos rinkinys. Lietuvos matematikų draugijos darbai, 56, 90–94.
35. Sičiūnienė, V., & Toleikytė, N. (2017). Are Teachers Paying Enough Attention to Low-achieving Students while Teaching Reading Strategies? Pedagogika, 127(3), 37–53.
36. De Smedt, F., & Van Keer, H. (2018). Fostering writing in upper primary grades: a study into the distinct and combined impact of explicit instruction and peer assistance. Reading and Writing, 31(2), 325–354.
37. Star, J. R., Rittle-Johnson, B., & Durkin, K. (2016). Comparison and Explanation of Multiple Strategies: One Example of a Small Step Forward for Improving Mathematics Education. Policy Insights from the Behavioral and Brain Sciences, 3(2), 151–159.
38. St Clair-Thompson, H. S. (2015). Lucid Recall Administrator’s Manual. Lucid Research Ltd.
39. TIMSS Report 2015: Mathematics. Grade 4, 2016. Retrieved from http://timss2015.org/wp-content/uploads/filebase/full%20pdfs/T15-International-Results-in-Mathematics-Grade-4.pdf
40. Toleikytė, N. (2014). Skaitymo strategijų mokymas(is) [Teaching Reading Strategies]. Gimtasis žodis, 1, 13–24.
41. Tracy, B., Reid, R., & Graham, S. (2009). Teaching young students strategies for planning and drafting stories: The impact of self-regulated strategy development. The Journal of Educational Research, 102(5), 323–332.
42. VanDerHeyden, A. M., Witt, J. C., & Barnett, D. W. (2005). The emergence and possible futures of response to intervention. Journal of Psychoeducational Assessment, 23(4), 339–361.
43. Veselinov, D., & Nikolić, R. (2015). The possibilities of encouraging student's metacognitive strategies through heuristic-methodological instruction. Research in Pedagogy, 5(1), 67–83.