Selective Pressure Strategy in Multilevel Cooperative Coevolution for Solving LSGO Problems

Abstract

Continuous large-scale global optimization (LSGO) is a challenging task for a wide range of state-of-the art metaheuristic algorithms. This is due to the curse of dimensionality because the size of the search space grows exponentially with the increasing the number of variables. Thus, metaheuristics lose efficiency in solving LSGO problems. For increasing the performance of metaheuristic algorithms in solving LSGO problems, cooperative coevolution (CC) is used. CC-based metaheuristics have two main control parameters, which are the population size and the type of variable grouping. In this paper, a novel self-adaptive multilevel cooperative coevolution algorithm is proposed. The subcomponent optimizer of the proposed CC-based algorithm is SHADE. The proposed algorithm self-adapts the number of subcomponents and the population size during the optimization process. The complete title of the proposed algorithm is CC-SHADE-ML. We have evaluated the performance of the proposed algorithm on fifteen benchmark problems chosen from the LSGO CEC’2013 benchmark set. The performance of the CC-SHADE-ML algorithm has been evaluated using well-known mutation strategies and selection operators. We can conclude that mutation and selection operators make a significant impact in the performance of DE-based metaheuristics. All numerical experiments are proven statistically.

Keywords: Large-scale global optimization, multilevel cooperation coevolution, differential evolution

Introduction

Metaheuristics are successfully used in solving black-box optimization problems, see in Zhan et al. (2022). Potter and Jong (1994) have proposed cooperative coevolution (CC) framework, to increase the performance of the traditional genetic algorithm (GA) to solve continuous optimization problems. The core idea of CC is to divide an optimization problem into disjoint subcomponents and evolve them independently to each other. As authors noted, any optimizer (evolutionary algorithm) can be used to optimize subcomponents. This research work formed the basis for solving LSGO problems, see in Mahdavi et al. (2015). Later, it was found that CC is a good tool for solving large-scale global optimization (LSGO) problems.

In the last two decades, many CC-based approaches have been applied to increase the performance of metaheuristics for solving real-world LSGO problems (Dong et al., 2010; Maniadakis & Trahanias, 2005). There are three main CC branches depending on variable grouping type: static, random, and learning-based variable grouping.

Static grouping, this type of variable grouping was proposed in the paper of Potter and Jong (1994) for the first time. The main idea is to set the fixed number of subcomponents and to define variables in these subcomponents. It is a preferable grouping if a relationship between variables is known. However, many real-world LSGO problems are presented by a black-box model.

Random grouping, optimized variables can be placed in different subcomponents many times during the optimization process (Yang et al., 2008a). When a predefined number of fitness evaluation is reached or other termination conditions are fulfilled, an algorithm randomly mixes variables between subcomponents, also the number of subcomponents can be changed. The main idea of random grouping is to increase the probability that two or more non-separable variables will be in the same subcomponent.

Learning grouping, this grouping is based on finding the original interaction between variables using special experiments (Omidvar et al., 2014). Usually, learning-based grouping approaches increment each variable of fitness function and to track changes. Based on the changes, variables are grouped in subcomponents.

In practice, determining the true relationship between variables is a challenging task, because of unknown optimization problem properties. In static and random grouping, setting the arbitrary group size can lead to low performance of an algorithm. On the other hand, learning grouping needs quite a lot of function evaluations (FEs) to determine true connections between variables, and there is no guarantee that an EA will perform better using the discovered true connection between variables. Thereby, there is a need to develop a self-adaptive mechanism for the automatic selection of the number of subcomponents and the population size.

The rest of the paper is organized as follows: section 2 proposes CC-SHADE-ML, contains description of selection operators and mutation schemes, section 3 contains experimental setup and results of numerical experiments. Section 4 concludes the paper.

Problem Statement

An LSGO problem can be stated as a continuous optimization problem:

$f\left(\stackrel{-}{x}\right)\to \underset{\stackrel{-}{x}\in {D\subset R}^n}{\min },$ $f^{\mathrm{*}}=f\left(x^{\mathrm{*}}\right)\le f\left(\stackrel{-}{x}\right),\mathrm{}x\in D\subset R^n,$

where $f\left(\stackrel{-}{x}\right)$ is an fitness function to be minimized, $f:R^n\to R^1$, $\stackrel{-}{x}$ is an-dimensional vector of continuous variables, $D$ is the search space defined by box constrains $x_i^l\le x_i\le x_i^u,i=\stackrel{-}{1,n}$, $x_i^l$ and $x_i^u$ are the lower and upper borders of the-th variable, respectively, $x^{*}$ is a global optimum. It is assumed that the fitness function is continuous.

Research Questions

In course of the study the following questions were raised:

• What is the role of cooperative coevolution approach in solving LSGO problems?
• What is the role of selection operators in CC-based evolutionary algorithms in solving LSGO problems?
• What is the role of mutation schemes in CC-based evolutionary algorithms in solving LSGO problems?

Purpose of the Study

The answers to the issues raised above will help achieve the goal and contribute to the development of recommendations on parameters selection in CC-based evolutionary algorithms for solving LSGO problems.

Research Methods

Findings

In this section, experimental setup and results are presented. In the paper, the LSGO CEC’13 benchmark set, Li et al. (2013), has been used for evaluating the algorithm performance. Numerical experiments have been conducted according to the conditions of the LSGO CEC’2013 competition. This set consists of 15 continuous optimization problems. The number of variables of each problem is equal to 1000. The maximum number of fitness evaluations is 3.0E+06 in each independent run. The comparison of algorithms is based on the mean values, which are obtained in 25 independent runs. Numerical experiments have been performed on a computation cluster based on eight personal computers. The total number of computational threads is 128.

The performance of CC-SHADE-ML has been evaluated. All combinations of mutation schemes and selection operators have been compared between each other. The proposed CC-SHADE-ML algorithm has the following parameters. The set of subcomponents is equal to {5,10,20,50}. The set of the population size is equal to {25,50,100}. In SHADE, the size of the archive is 100. The number of cycles is set to 50. According to our numerical experiments, this value for the number of cycles performs better than other tested values. Thus, in each cycle, CC-SHADE-ML evaluates 6.0E+4 FEs.

Figure 1 presents how CC-SHADE-ML switches the number of subcomponents and the population size during the optimization process in one independent run on F₂ benchmark problem using current-to-pbest/1 mutation scheme and tournament selection. The x-axis shows FEs, the y-axis shows the levels of subcomponents and population size.

See Full Size >

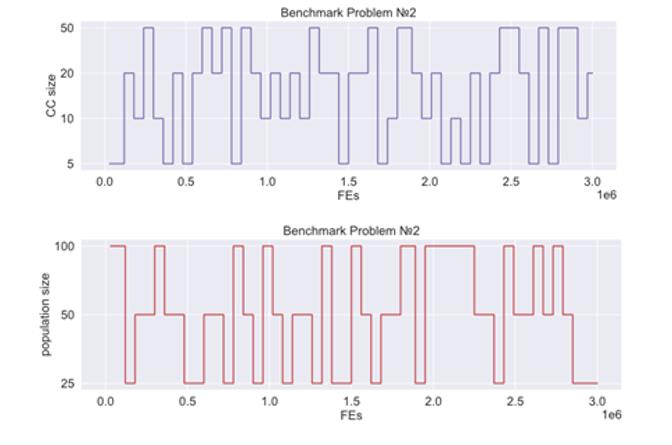
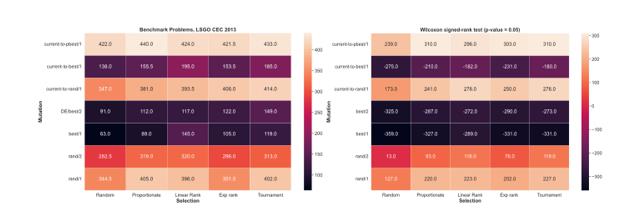
Figure 2 shows heat maps for each benchmark problem and each combination of mutation and selection. The x-axis denotes the selection type, the y-axis denotes the mutation scheme. The performance of each combination of mutation and selection is presented by rank. The biggest number corresponds to the best average fitness value obtained in 25 independent runs. Dark blue (dark) and white color (light) colors denote the best and worst combination, respectively. The rank distribution in heat maps depends on the optimization problem.

Figure 3 shows the rank sum for the algorithm’s parameters for all benchmark problems (left) and the sum of scores based on comparison using the Wilcoxon rank-sum test (left). The x-axis denotes the selection type, the y-axis denotes the mutation scheme. The highest sum is the best achieved result. The dark color denotes the worst on average combination of parameters. The results in the left picture are based on the results from Figure 2. The results in the right picture are based on pairwise comparison corresponding combinations with other combinations on all benchmark problems. If statistical significance is found between two combinations on a problem, then add one score to the best-performed combination and remove one score from the other.

See Full Size >

Conclusions

The paper proposes the CC-SHADE-ML algorithm for solving large-scale global optimization problems. CC-SHADE-ML changes the number of subcomponents and the number of individuals based on their performance. We have investigated the proposed metaheuristic using the LSGO CEC’13 benchmark set with fifteen benchmark problems. Numerical experiments show that the best-performed mutation scheme, on average, is the current-to-pbest/1, the best-performed selections are tournament and proportionate selection. All experiments are proven by the Wilcoxon test. CC-SHADE-ML has a high potential for enhancement. In our further works, we will improve the performance of the CC-SHADE-ML algorithm by modifying the optimizer and tuning the parameters of selections. Also, we will test the use of hybrid memetic metaheuristics for solving continuous large-scale global optimization problems.

See Full Size >

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.

References

• Dong, X., Yu, H., Ouyang, D., Cai, D., Ye, Y., & Zhang, Y. (2010). Cooperative coevolutionary genetic algorithms to find optimal elimination orderings for bayesian networks. In 2010 IEEE fifth international conference on bio-inspired computing: Theories and applications (BIC-TA) (pp. 1388-1394). IEEE. DOI:

  Google Scholar

  Crossref

• Li, X., Tang, K., Omidvar, M. N., Yang, Z., & Qin, K. (2013). Benchmark functions for the CEC’2013 special session and competition on large scale global optimization. Technical Report, 1-23.

• Mahdavi, S., Shiri, M. E., & Rahnamayan, S. (2015). Metaheuristics in large-scale global continues optimization: A survey. Information Sciences, 295, 407-428. DOI:

  Google Scholar

  Crossref

• Maniadakis, M., & Trahanias, P. (2005). A hierarchical coevolutionary method to support brain-lesion modelling. Proceedings. 2005 IEEE International Joint Conference on Neural Networks (pp. 434-439). DOI:

  Google Scholar

  Crossref

• Omidvar, M. N., Li, X., Mei, Y., & Yao, X. (2014). Cooperative Co-Evolution with Differential Grouping for Large Scale Optimization. IEEE Transactions on Evolutionary Computation, 18(3), 378-393. DOI:

  Google Scholar

  Crossref

• Potter, M. A., & Jong, K. A. (1994). A cooperative coevolutionary approach to function optimization. Parallel Problem Solving from Nature — PPSN III, 666, 249-257. DOI:

  Google Scholar

  Crossref

• Tanabe, R., & Fukunaga, A. (2013). Success-history based parameter adaptation for differential evolution. In 2013 IEEE congress on evolutionary computation (pp. 71-78). IEEE. DOI:

  Google Scholar

  Crossref

• Yang, Z., Tang, K., & Yao, X. (2007). Differential evolution for high-dimensional function optimization. In 2007 IEEE congress on evolutionary computation (pp. 3523-3530). IEEE. DOI:

  Google Scholar

  Crossref

• Yang, Z., Tang, K., & Yao, X. (2008a). Large scale evolutionary optimization using cooperative coevolution. Information Sciences, 178(15), 2985-2999. DOI:

  Google Scholar

  Crossref

• Yang, Z., Tang, K., & Yao, X. (2008b). Multilevel cooperative coevolution for large scale optimization. In 2008 IEEE congress on evolutionary computation (IEEE World Congress on Computational Intelligence) (pp. 1663-1670). IEEE. DOI:

  Google Scholar

  Crossref

• Zhan, Z.-H., Shi, L., Tan, K. C., & Zhang, J. (2022). A survey on evolutionary computation for complex continuous optimization. Artificial Intelligence Review, 55(1), 59-110. DOI:

  Google Scholar

  Crossref