Using Geogebra To Teach Parametric Problem Solving

Abstract

Today, digital tools are an integral part of learning. The past two years showed that the use of information technologies in professional activities is a vital skill for teachers at all levels and in all fields of education. At present, a software product can be chosen for every lesson on any subject to help students in mastering it and help a teacher explain the related material. Parameter problems are considered to be the most difficult type of mathematics at school. In particular, it is complicated to understand the nature of the problems, and methods of solution. This article describes one of the instructional techniques of using GeoGebra while studying the topic The circle equation to further teach students to solve parameterized equation systems on the circle combination. The author’s choice of GeoGebra is proved by its intuitive intelligibility and the Cyrillic interface, as well as by the fact that there is no need to install the program on a personal computer. The guidance software proposed in the article has been tested within the further curriculum for schoolchildren at MIP School: Mathematics, Informatics, and Physics set up at Sholom- Aleichem Priamursky State University.

Keywords: Circle equation, GeoGebra, graphic approach, [arametric problem

Introduction

Present-day education is impossible without digital tools for different purposes. A variety of learning software products has greatly expanded the range of instructional techniques. Nowadays, for every topic of any subject, a digital tool can be selected to help students in mastering it and, to explain the proper material for a teacher. (Aliyu et al., 2021; Daher, 2021; Kusumah et al., 2020; Larin & Mayer, 2018; Podaev et al., 2021; Semenikhina & Drushlyak, 2015).

One of the difficult methodological objectives of an educator is to teach students to solve parameter problems. The questions of how to guide students to understand the notion of ‘parameter’ better, how to teach to solve different types of parameter problems, how to explain the core of different methods of solving such problems are still very popular in the methodological and scientific literature (Dalinger, 2020; Ledovskikh et al., 2020; Matveeva et al., 2020; Sevryukov & Smolyakov, 2018; Shabashova, 2019). The introduction of available and user-friendly software packages that allow illustrating the dynamics of parameter value change in a problem graphically makes it possible to make a being of the parameter in the problem clear, as well as to explain solution methods related to the construction of geometric and iconic format of equations, inequations and their parameter systems. One such resource is the GeoGebra environment.

GeoGebra is an open-source software package combining algebra, geometry, graphics, spreadsheets, statistics and computation that allows one to explore algebraic and geometric entities in their progress at one time. The GeoGebra environment has an intuitive (user-friendly) interface, provides the opportunity of operating in Russian. It does not require installation on a personal computer and perform many powerful functions. These and other advantages make GeoGebra a convenient methodological aid for teaching Mathematics at different learning levels. The possibility of collaborative work in GeoGebra enables us to use it not only for full-time education but also for distance learning.

The popularity of the GeoGebra environment not only for teachers but also for methodologists is confirmed by a lot of current publications devoted to the emergence of its capabilities while studying various topics in elementary mathematics, for example, in the course of ‘Solving parameter problems’ (Kusumah et al., 2020; Kashitsyna, 2020; Kurilova & Stepanova, 2020; Troyakova et al., 2018). Among many works illustrating the possibilities of computer animation in GeoGebra when studying many sections of mathematics, we should mention the series of works written by Larin (2020). In particular, Larin (2020) gives the most complete description of the possibilities of GeoGebra dynamic tools in various sections of elementary and calculus.

Problem Statement

The study of parameter problems begins with an examination of the concept of a parameter. Here, the first challenge is for a teacher to explain and for a student to understand what the difference between a parameter and a variable is, that each parameter problem is not just one problem, but a whole class of problems. Using the simplest tools of the GeoGebra environment makes it easy to explain the function of the parameter in the problems, as well as let the students move smoothly to one of the geometric approaches to solving parameter equations and equation systems.

One more difficulty of parameter problems is related to the large variety of methods and special techniques for solving them. The same task can be solved in different ways, and the amount of time and effort spent on finding an answer depends considerably on the successful or unsuccessful choice of method. Methods involving the construction of graphical representations usually result in the most space-saving and rational decisions. The GeoGebra environment allows one to observe the dynamic change in the graphical illustration of equations, inequalities, and equation systems containing one or more parameters on the screen.

Research Questions

Taking into account the variety of types of parameter problems, we will focus only on the problems resulting in the study of the mutual arrangement of circles and arcs of circles within this research The main part of the paper describes a universal instructor’s manual that allows, after studying the topic ‘Circle equation’, to proceed to an explanation of the concept of ‘parameter’ and, then, to the solution of a parameter equation systems. The universal character of that a similar scheme can be introduced when studying other topics, for teaching the solution of parameter problems of other types.

It should be noted that before starting to explain the task described below, it is necessary to achieve students’ understanding of the functions of all components of the general circle equation, the skill of constructing a circle according to its equation in the Cartesian coordinate system in the plane. It is also supposed to introduce students to the GeoGebra formula combination language.

Purpose of the Studу

The purpose is to investigate the opportunities of the GeoGebra environment in teaching parametric problem solving using graphical and geometric techniques.

Research Methods

The research is based on the system-activity approach in education, focused, in particular, on the active learning and cognitive activity of students. The first stage of the study involved the review of scientific publications and pilot-testing for hypothesis verification.

Findings

The first proposed task is divided into three stages. The preparatory stage is presents updating the knowledge of the circle equation, a formula composition in GeoGebra. The advancement stage introduces parameters to the circle equation. The simultaneous study of an algebraic formula and its geometric image on the screen allows one to make the function of the parameter in the equation clear. The main task is designed to develop a comprehension of the fact that the same parameter, can be presented in different formulas and have a different effect on the type of the geometric image and the mutual arrangement of the circles relative to each other. As shown in Table 1.

See Full Size >

See Full Size >

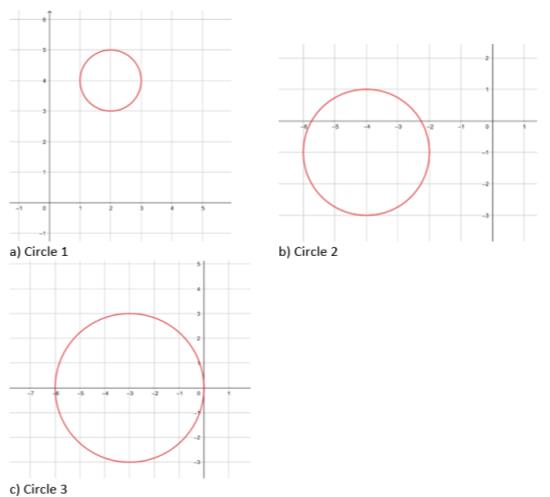
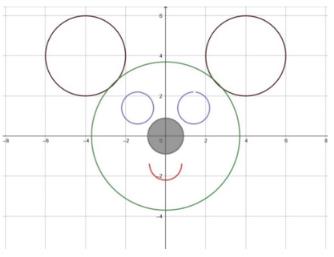
You may use the following system of assignments to examine the parameter equation systems on the mutual arrangement of circles.

Problem 1. How should the values of parameters a and b be correlated to make the ears go down the head only?

Problem 2. How should the values of parameters c and d be correlated so that the two eyes are in contact with each other?

Problem 3. For what values of the parameter a does the system $\left\{\begin{array}{c}{\left(x-\mathrm{3}\right)}^{\mathrm{2}}+{\left(y+\mathrm{1}\right)}^{\mathrm{2}}=\mathrm{1}\\ x^{\mathrm{2}}+y^{\mathrm{2}}=a^{\mathrm{2}}\end{array}\right.$ have only one solution?

Before solving the third task, it is useful to

• Draw circles in GeoGebra and use the slider to consider all possible variations of mutual arrangement of circles (Fig. 3);
• discuss two possible variations of tangent circles (Fig. 3);
• find approximate parameter values for the tangent variations;
• use the Intersection tool to display the intersection points of the circles, and try to find more accurate parameter values for the tangent variations (see Figure 3).

See Full Size >

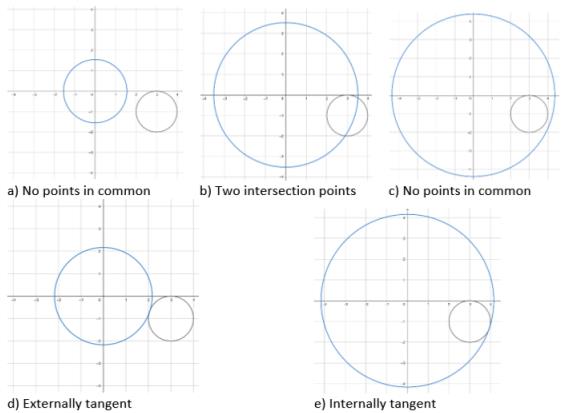
At the end of this assignment, one should use calculations to find the exact solution to the problem.

Since parameter a is squared in the second equation, consider non-negative values of the parameter in the solution, then a can be geometrically interpreted as a circle radius. Denote the radii of fixed and sliding circles by $R_{\mathrm{1}}$and $R_{\mathrm{2}}$ respectively:

$R_{\mathrm{1}}=\mathrm{1},\mathrm{}{R}_{\mathrm{2}}=a.$

The distance between the circle centers is:

$d=\sqrt{\mathrm{9}+\mathrm{1}}=\sqrt{\mathrm{10}}.$

The required values of the parameter:

• for externally tangent R1+R2=d,soa=±10-1;
• for internally tangent R2=R1+d,soa=±10+1.

After a complete examination of the given system of equations, a combined answer might be given to the number of the system solutions for all possible values of the parameter:

• at a=10-1, a=10+1 the system has a unique solution;
• at 10-1<a<10+1 the system has two solutions;
• at a<10-1,a>10+1 the system has no solution.

The use of GeoGebra tools does not replace the need to understand mathematical terms. It is only a way of visualization, a means for explaining the material. In this case, the ultimate goal is to teach students to solve parameter problems independently, i. e. without using additional digital tools. In the system observed, the answer involves irrational numbers, so it is not possible to solve it exactly with GeoGebra.

Task 4. Examine the number of solutions of the system $\left\{\begin{array}{c}{\left(x-a\right)}^{\mathrm{2}}+{\left(y+\mathrm{1}\right)}^{\mathrm{2}}=\mathrm{1}\\ {\left(x+\mathrm{1}\right)}^{\mathrm{2}}+y^{\mathrm{2}}=a^{\mathrm{2}}\end{array}\right.$ depending on the parameter $a$.

In this problem, the same parameter is present in both equations but performs different functions. In the first case, it is responsible for the location of the centre of the circle, while in the second, for the radius of the circle. Having drawn both circles, when increasing a modulo parameter a, there is an illusion of tangency between two circles: it looks like an internal tangency for negative values, whereas it looks like an external tangency for positive values. It happens because of the natural desire to zoom to follow the behaviour of both circles. If we zoom in close enough to the apparent tangency, one can see that for arbitrarily large modulo values of a the circles intersect at two points (for negative a) or have no points (for positive a) https://www.geogebra.org/m/pbtdm26w. If there are or there are no intersection points of the circles available- that can be observed when the corresponding Intersection tool is applied.

Now it is not difficult to find when there is a transition from no common points to an intersection, i.e. when two circles are tangent by changing the parameter value with the slider. In this case, the corresponding value of the parameter is exactly a=-0.25. Nevertheless, it is necessary to verify analytically that there are no other changes to the mutual arrangement of the circles.

Denote the radii of the first and second circles by $R_{\mathrm{1}}$ and $R_{\mathrm{2}}$ respectively:

$R_{\mathrm{1}}=\mathrm{1},\mathrm{}{R}_{\mathrm{2}}=\left|a\right|.$

The distance between the centres of the circles $O_{\mathrm{1}}\left(a,\mathrm{}-\mathrm{1}\right){\mathrm{и}\mathrm{}O}_{\mathrm{2}}\left(-\mathrm{1},\mathrm{}\mathrm{0}\right)$:

$d=\sqrt{{\left(a+\mathrm{1}\right)}^{\mathrm{2}}+\mathrm{1}}.$

In case of the external tangency $R_{\mathrm{1}}{+R}_{\mathrm{2}}=d$:

$\mathrm{1}+\left|a\right|=\sqrt{{\left(a+\mathrm{1}\right)}^{\mathrm{2}}+\mathrm{1}}.$

The resulting equation has no solutions for positive values of a, for a<0 we obtain the equation after exposing the modulus:

$\mathrm{1}-a=\sqrt{{\left(a+\mathrm{1}\right)}^{\mathrm{2}}+\mathrm{1}},$

$a=-\mathrm{0,25}.$

In case of the internal tangency, theoretically, two variations are possible:

Answer: a<-0.25, the system has two solutions,

a=-0.25, the system has only one solution,

a>-0.25, the system has no solutions.

Task 5. Find all the values of the parameter a when the system $\left\{\begin{array}{c}{x}^{\mathrm{2}}+y^{\mathrm{2}}-\mathrm{4}x-\mathrm{4}=\mathrm{8}\left|x+y-\mathrm{2}\right|\\ {\left(x-\mathrm{2}\right)}^{\mathrm{2}}+y^{\mathrm{2}}=a^{\mathrm{2}}\end{array}\right.$ has more than two solutions.

The previous definitions were quite simple options of the parameter assignments on combinations of circles. The equations of circles in the systems are not often given in the canonical form. In other words, they must first be transformed in such a way that they are first written as easy as to interpret geometrically. Moreover, a second-degree equation may assign combinations of arcs of circles and/or straight lines (rays) from x and y variables. Whereas the previous assignments contained only individual circles and semicircles, the fifth assignment contains a composition of arcs of circles and it requires the skills of modulo revealing, understanding that semicircles define linear inequalities from the variables x and y in the coordinate plane for solving.

The first equation of the system $x^{\mathrm{2}}+y^{\mathrm{2}}-\mathrm{4}x-\mathrm{4}=\mathrm{8}\left|x+y-\mathrm{2}\right|$ after developing a modulus, results in two arcs of circles, which are connected at coordinates $\left(\mathrm{0},\mathrm{}\mathrm{2}\right)$ and $\left(\mathrm{4},\mathrm{}-\mathrm{2}\right)$ thus generating a weeble wobble (Fig. 4): $y<\mathrm{2}-x$ $y>\mathrm{2}-x$

Of course, the study of the first equation requires rigorous research, but within this article, the author focuses more on the application of the GeoGebra environment.

The second equation defines a family of concentric circles centred at the point $O\left(\mathrm{2},\mathrm{}\mathrm{0}\right)$ of radius $\left|a\right|$ (at $a=\mathrm{0}$ the circle becomes a point) (Figure 4).

See Full Size >

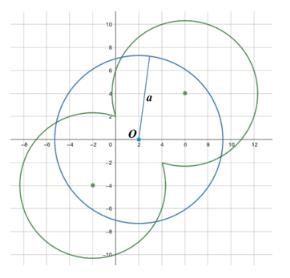
By changing the value of the parameter, a, we obtain three possible variations of mutual arrangement of the weeble wobble and the circle:

• no points in common;
• two common points;
• four common points.

Let us find the values of the parameter a that correspond to two common points (Figure 5).

See Full Size >

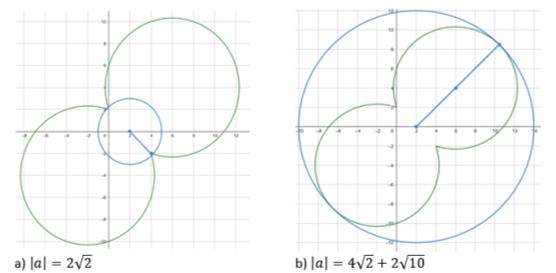
The final answer is the following: at $\mathrm{2}\sqrt{\mathrm{2}}<\left|a\right|<4\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{10}}$ the system has more than two solutions.

Conclusion

The teaching aid proposed in the article has been tested while actualizing the extended curriculum for schoolchildren School MIP: Mathematics, Informatics, Physics started as part of Sholom-Aleichem Priamursky State University. As this experience proves, students begin to be good at other definitions of the parameter problems on the mutual arrangement of circles quite quickly, and it is easier for them to come down from algebraic to geometrical definitions of problems.

References

• Aliyu, J., Osman, S., Daud, M. F., & Kumar, J. A. (2021). Mathematics teachers' pedagogy through technology: a systematic literature review. International Journal of Learning, Teaching and Educational Research, 20(1), 323-341.

• Daher, W. (2021). Middle school students’ motivation in solving modelling activities with technology. Eurasia Journal of Mathematics, Science and Technology Education, 17(9), 1-13.

• Dalinger, V. A. (2020) Matematika: zadachi s parametrami [Mathematics: parameter problems]. Yurayt.

• Kashitsyna, Y. N. (2020). Metodika obucheniya resheniyu zadach s parametrami s ispol'zovaniyem programmy «Geogebra [Methodology of teaching parameter problem solving using ‘Geogebra’ software]. World of Science, Culture, Education, 1, 249-255.

• Kurilova, O. L., & Stepanova, E. A. (2020). Primeneniye sredy Geogebra pri reshenii zadach s parametrami (disk-prilozheniye k zhurnalu) [Application of the Geogebra environment in solving parameter problems (journal disc supplement)]. Mathematics at school, 4, 44.

• Kusumah, Y. S., Herman, T., & Kustiawati, D. (2020) The effect of GeoGebra in three-dimensional geometry learning on students' mathematical communication ability. International Journal of Instruction, 13(2), 895-908.

• Larin, S. V. (2020). Metodika obucheniya matematike: komp'yuternaya animatsiya v srede Geogebra [Methods of teaching mathematics: computer animation in Geogebra environment]. Moscow: Yurait.

• Larin, S., & Mayer, V. (2018). The role of computer animation in mathematics teaching. Mathematics and Informatics, 61(6), 542-552.

• Ledovskikh, I. A., Gorbaneva, L. V., & Zhudilova, Y. V. (2020). Zadachi s parametrami: s chego nachat' [Parameter Problems: where to start]. International research journal, 11(3), 107-111.

• Matveeva, T. A., Svetlichnaya, V. B., Mustafina, D. A., Rebro, I. V., & Rakhmankulova, G. A. (2020). Osobennosti metodov resheniya nestandartnykh zadach po matematike s parametrami [Peculiarities of methods for solving non-standard parameter problems in mathematics]. Modern Issues of Science and Learning, 2, 39.

• Podaev, M. V., Podaeva, N. G., & Agafonov, P. A. (2021). Development of the activity of gifted schoolchildren in mastering geometric concepts in figurative structures. Propositos y representaciones, 9(S3), e1126.

• Semenikhina, E.V., & Drushlyak, M.G. (2015). Programmy dinamicheskoy matematiki: kolichestvennyy analiz v kontekste podgotovki uchitelya matematiki [Dynamic mathematics programs: quantitative analysis in the context of mathematics teacher training]. Information technologies and teaching tools, 48(4), 35-46.

• Sevryukov, P. F., & Smolyakov, A. N. (2018). Shkola resheniya zadach s parametrami [School of parameter problem solving]. Ileksa, Stavropol: Service School.

• Shabashova, O. V. (2019). Sistema zadaniy kak sredstvo formirovaniya umeniy primenyat' funktsional'no-graficheskiy metod dlya resheniya zadach s parametrami [The system of tasks as a means of developing skills to apply the functional-graphic method for solving parameter problems]. Mathematics at School, 5, 43-59.

• Troyakova, G. A., Mongush, A. S., & Tanzy, M. V. (2018). Metodika podgotovki uchashchikhsya k resheniyu zadach s parametrami s ispol'zovaniyem sredy Geogebra [Methodology of training students to solve parameter problems using Geogebra environment]. The world of Science, Culture, Education, 5, 27-35.