Abstract
The article examines the business success of the organization. The indicators that manifest it have values with fuzzy set characteristics. They are subject to the rules of fuzzy sets, which are discussed in this article. We believe that business success is a measurable concept since it can be decomposed into components and draw a path between them if we take the elements of business success and their display as these components. The article shows that the proposed definition of business success is correct. It can be used for detailed analysis and decomposition of an organization into subelements (subsets) that play an essential role. This author's approach will significantly complement the existing methods of assessing business success, since it mathematically connects business success with the choice of an organization at a time, which has not been previously used by any of the Russian and foreign authors. It should be noted that Russian and foreign authors characterize the concept of business success and methods of its assessment in different ways, on the basis of which we have adopted an attempt to develop a completely new approach to this issue. The paper provides examples showing a parallel between our theoretical assumptions based on mathematical methods and existing facts, highlighting the advantages of the author's approach. The article was prepared in connection with the weak study of this issue by researchers from mathematical methods and existing theories of other sciences.
Keywords:
Introduction
Business success is a fairly broad category that includes various quantitative and qualitative parameters. Predicting the level of business success is complicated by considering the qualitative components of an organization's business success (for example, the quality of management). Qualitative parameters can be described using cognitive modeling. However, there is no common understanding of what the business's business success is related to and its structure, which is a significant problem in the study of organizations and economic entities. The question of interpretation of the concept and factors influencing business success has been studied by many Russian and foreign authors (Aaker, 2014; Ćurčić & Miletić, 2020; Diah & Safrida, 2018; Matuzenko et al., 2016; Ponomarenko, 2019; Pletnev & Barkhatov, 2019; Pletnev & Nikolaeva, 2018; Pletnev & Nikolaeva, 2020; Strelchenko, 2019 and others). However, to date, there is no consensus regarding business success, which makes the issue of solving this problem even more necessary and relevant.
Problem Statement
Note that the existing approaches to the study of business success do not provide an objective solution for its measurement due to the wide variety of approaches. Drucker in 1954 proposed the methodology of "management by goals", considering that this is a factor in the organization (Drucker, 2003). Knyazhev in the work on the coordination of interests of owners and managers sees the problem of development in non-legalized relations between the parties. The moral and ethical climate as a factor of business success in the team is also important for the success of the organization, according to Knyazhev (2011). Many authors have suggested developing a comprehensive method that includes both a functional method that involves the study of external relations, and a situational method that involves studying dynamics within an organization. In General, we note that none of the above authors in their works showed sufficient certainty of the question – what is the difference between successful organizations and less successful ones. Most authors' research is quite spontaneous, has no structure, and is not considered from different sides and horizons of the existing economy. There is no complete concept or scientific methods for understanding the success of an organization. The works considered by us are characterized by a lack of quantitative indicators, and most importantly, theoretical and practical evidence of the methods used by them.
Research Questions
The authors set a goal: to study business success from the point of view of similarity with sets, as well as to apply to business success the theorems that are used in the study of sets, thereby mathematically, more objectively clarify the definition of business success.
Purpose of the Study
Focusing in detail on the set counting theorem, we have found practical evidence that the more elements that make up business success are taken into consideration, the more achievable the organization's successful activity;
Research Methods
The method is based on a comparison of economic and mathematical methods in Economics, as well as Cantor's theorem on the power of sets (Pryakhin et al., 2019a). The main difficulty was in choosing sources and methods of work that would ensure the reliability of the data obtained and contribute to obtaining reliable conclusions. We have researched scientific literature terms about sets and their relationships, as well as scientific publications about the evaluation of organizations and approaches to the study of business success;
Findings
Consider the activities of the most successful large firms. If, for example, we take the dynamics of the value of Apple shares over the past 30 years, we will see an increase and decrease in this value over time. Undoubtedly, this cost is influenced by various factors, both external and internal. These factors may include new products or technologies from competitors, legal issues related to the organization's foreign economic activity, quarterly or annual reporting indicators, interviews with members of the Board of Directors, etc. It can be seen that there are certain factors that have both a positive and negative impact. Note that the external factor exists and has a significant impact. So in the presence of driving factors, the stock price goes up, as well as with restraining factors, it slows down or turns in the opposite direction.
Take, for example, the growth of smartphone sales in the world over the past fifteen years, we see that the driving force also influences this growth. In this case, it is the increasing convenience of such devices in everyday life.
Thus, if an element exists, it is a set, i.e. a set United by a certain rule, a set, collection, or collection of some object with characteristic properties.
A set can enter into various relationships with its elements. This can be seen from the author's figure
From figure
We assume that the existence of business success implies the existence of a set of business success. Sets have some properties that also occur as elements of an organization.
“x” is included in “A”, since each part of “x” belongs to “A”. The " x” element here is Finance. This belongs to business success in General.
2. "x" includes "A" because "A" is included in "x". The financial side includes business success since business success is also the financial side that determines economic financial coefficients and stability in General.
3. "x” is equal to “A", since “A” and “x” are included in each other. Business success affects finances completely, just as business success itself depends on them.
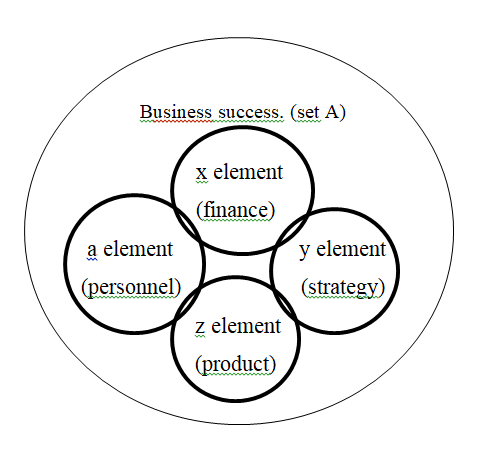
4. " x” is strictly included in “A”, since “x” is included in “A”, and they are not equal to each other (from set theory). It is obvious that business success is included in all areas of the organization, while business success – increasing the volume of business, efforts, creating new business areas, etc.
5. “x” strictly includes “A”, since “A” is strictly included in “x”.
6. " A” and “x” intersect because they have common elements. For example, strategy is a common element for Finance and business success.
7. “A” and “x” are in a General position, since “y” belongs exclusively to “A“, belongs exclusively to” x", and belongs exclusively to both sets. Business success, respectively, belongs to both elements.
The revealed similarity of soft factors with sets allows us to state, based on set theory, that no more than a countable Union of no more than countable sets is no more than a countable one.
We have a business success of the organization, which, presumably, is no more than countable, that is, it has the form N – natural number 0, 1, 2, 3, ... n-1 (Ilyin et al., 2006).
Business success is definitely influenced by various factors – revenue, profit, amount of borrowed funds, etc. (let's call it A1, A2, A3, AP). It is also influenced by other factors – market conditions, global trends, culture, geopolitics, etc. (let's call this AP+1, provided that it can be +1 – favorable and -1-not favorable, that is, counting), which is also a subset of the set of business success.
It follows from the set theorem that if the set of business success is countable, then all subsets are also countable. When proving the theorem, the elements must not be an empty set, i.e. 0, otherwise it is obvious that there are no financial indicators and there is no business success. Therefore, if there are financial indicators, especially natural numbers, then there is something in the Union as well.
In the field of business success, as we said above, that, something is also there, means a mathematical mapping in A, or
h:N A.
The set of values of a mapping that has the set A, that is:
h (N) An, that is, the values of business success are displayed in its elements. This is a record of the theorem that business success sets are no more than countable.
Also, the set of values of An elements have their own mappings, that is, for each N there are mappings f (N) from the set of natural numbers An for An> 0, which means that the set of values of An is natural numbers (Figure
The function writes the dependence of business success on elements:
F0 (0) F0 (1) F0 (2) F0 (3) ...
F1 (0) F1 (1) F1 (2) F1 (3) ...
F2 (0) F2 (1) F2 (2) F2 (3) …
…
Where F 0,1,2...n – any Association (in our case – business success)
Fn (1), Fn (2), Fn (3) the members of the Association (in our case – frames, strategy, product, etc.)
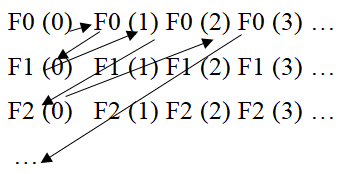
This is a graph of the set of natural numbers, composed by sequential traversal of elements. For each element of the table, you can understand at what step this or that element will meet, that is, how long the path will be, and at this position this element will meet.
Thus, we can present this image to our Association – business success.
We assume that the larger the size of the Association, the more sustainable the organization is. However, note that from the same set theorem, only elements without intersections must be selected. If elements overlap, these elements must be removed from the Union.
In practice, this can be described as follows. For example, Well Fargo experienced serious difficulties in 2008-2009. In the late 1980s, before the company's meteoric rise, Well Fargo began hiring top executives, sometimes without even knowing what position to fill. This process was later called the “injection of managerial talent". Reichard Karl, who headed this company, later established more associations with highly qualified specialists, thereby expanding his success.
In the late 90's, ABB, which was engaged in various types of production, including trains and trams, began to move to financial services. People believed in the company, which was one of the biggest companies in the US, by investing in its shares. This means that in the late 90's, the company began to move away from its core activities, while still showing good performance in terms of share price, despite the fact that revenue dynamics began to decline.
We assume that the organization has established too many overlapping links, and therefore elements have started to be removed, reducing the counting parameter of successful activity.
If we consider the share price of Toyota Motor again, we will see that since the beginning of the 80-ies, the company began to enter the world automobile markets, taking advantage of the oil crisis, as it produced fuel-efficient cars. With the highest corporate culture, lean production system, product quality, and reasonable price, Toyota shares show stable and high growth.
Back to Well Fargo. In addition to it, other organizations also hire top managers. However, Well Fargo hired them more correctly.
For every family X of non-empty sets, there is a function f that graph one of this set elements to each set of the Family (Baghani et al., 2016).
Suppose, F0 (3) is a top management selection model (Figure
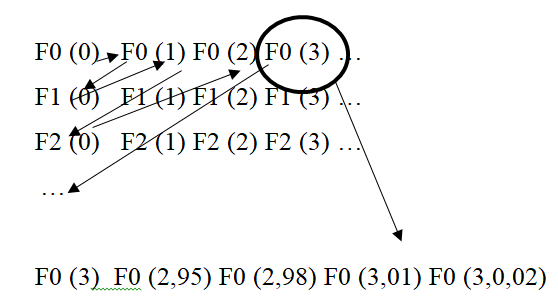
Referring to Cantor's theorem, which States that any set A is less powerful than the set of all its subsets A^2, shows that the Union of detail F0 (3) is more powerful than F0 (3). In other words, many funds are part such as accounting, cash flows, Bank rate, etc., and their Union is more powerful than Finance, they are a part. I.e. in any situation there are subsets that are, as parts of a situation, not hers, and therefore, do not exist for the situation (Bottazzi et al., 2019). A regime is needed to prevent the formation of such Hausa zones. This mode is the opinion of various authors about the representation and measurement of business success.
In this article, we assume the existence of business success as a counting object, although without a specific description of it. However, we believe that if we cannot use complete ordering, then our choice is not quite explicit (Da Silva, 2019). If an organization can't order unions, it makes an implicit choice with a margin of error up to the axiom of choice.
Thus, business success cannot include all the elements defined only in terms of business success and other elements that imply business success in their definition.
So, the authors propose a new approach to the consideration of business success, namely, business success implies the existence of a set of business success. This business success set has some properties, such as the inclusion of one element of business success in another, the intersection of elements. The revealed similarity of soft factors with sets allows us to state, based on set theory, that no more than a countable Union of no more than countable sets is no more than a countable one. In other words, business success is a counting parameter. Based on this, we assumed that the larger the size of the Association, the more sustainable the organization is. The second element of novelty is that when we break down an element of business success into its parts, we consider combining its components with being more assertive. Cantor), which suggests the need to study the components of the elements of business success. We also note that the paradox of Cantor's theorem has the consequence that there is only one choice for a given moment (one component of the element of business success), while other components do not exist (Mycielski & Tomkowicz, 2018). We believe that this paradox is regulated by a specific regime, which is the authors' opinions about business success and its methods.
Conclusion
We have proposed a new approach to the definition of business success, using the similarity of business success with the mathematical category of sets. In practice, we have found confirmation of our theory that the more elements an organization understands, the more accurate its actions lead the organization to business success. So, Well Fargo hired top managers. More precisely, we solve the problem of human resources. On the contrary, ABB greatly diversified its activities, thereby creating too many chaotic relationships. It led to the matrix increase (3), from which all the repeating elements were removed, but the lost time was not returned. These examples demonstrate our approach's viability, which is based on a mathematical approach to the study of business success.
This work will complement existing methods to determine and investigate business success with mathematical categories such as sets, Cantor's theorem, and properties inherent in sets and business success. We believe this approach is particularly relevant in the run-up to the fourth industrial revolution, the increasingly complex market environment, and globalization.
References
- Aaker, D. (2014). Aaker on Branding: 20 Principles that Drive Success. New York, NY: Morgan James Publishing.
- Baghani, H., Gordji, M. E., & Ramezani, M. (2016). Orthogonal sets: The axiom of choice and proof of a fixed point theorem. Journal of Fixed Point Theory and Applications, 18(3), 465-477.
- Bottazzi, E., Kanovei, V., Katz, M., Mormann, T., & Sherry, D. (2019). On mathematical realism and applicability of hyperreals. Matematychni Studii, 51(2), 200-224. https://doi.org/10.15330/ms.51.2
- Ćurčić, N., & Miletić, V. (2020). Factors important for achieving the competitiveness of industrial and agroindustrial products. Ekonomika poljoprivrede, 67(3), 831-847.
- Diah, M., & Safrida, F. (2018). Analysis of factors affecting business success of micro and small enterprises: a study of food and beverage enterprises in banda aceh. RJOAS, 12(84), 113-117. https://doi.org/10.18551/rjoas. -12.15
- Da Silva, S. G. (2019). On uniformly continuous functions between pseudometric spaces and the Axiom of Countable Choice. Archive for Mathematical Logic, 58, 353–358.
- Drucker, P. F. (2003). Management practice. Moscow: ID “Williams".
- Ilyin, V. A., Sadovnichy, B. L., & Sendov, Kh. (2006). Veshchestvennyye chisla. Matematicheskiy analiz [Real number. Mathematical analysis]. Moscow: Prospect.
- Knyazhev, O. V. (2011). Interesy sobstvennikov i upravlyayushchikh: kak izbezhat' konfliktov? [Interests of owners and managers: how to avoid conflicts?]. Russian entrepreneurship, 12(8), 76-80.
- Matuzenko, E. V., Shilenko, S. I., & Fedorova, Ya. O. (2016). Delovyye kommunikatsii kak faktor povysheniya rezul'tativnosti biznesa [Business communication as a factor of increasing the effectiveness of business]. Fundamental research, 9-3, 622-627.
- Mycielski, J., & Tomkowicz, G. (2018). Shadows of the axiom of choice in the universe. Archive for Mathematical Logic, 57, 607–616,
- Pletnev, D., & Nikolaeva, E. (2018). Successful Practices of Russian Medium – Size Enterprises. Eurasian business perspective. Eurasian studies in business and Economics, 8/1, 131-140.
- Pletnev, D., & Nikolaeva, E. (2020). Integral Evaluation of Business Success: Methodology and Case of Russian SME. VIII International Scientific Siberian Transport Forum, 643-656.
- Pletnev, D., & Barkhatov, V. (2019). Ups and Downs of High-Growth Firms in Russia. International Symposium in Management (SIM2019), 127-136.
- Ponomarenko, E. (2019). Research methodology for the assessment of the influence of organizational culture aspects on project success. Perm University Herald, 14(3), 495-512.
- Pryakhin, G. N., Trukhanov, D. A., & Maltsev, Yu. G. (2019a). Delovoy uspekh v prostranstvenno - vremennykh koordinatakh [Business success in space - time coordinates]. Azimuth of scientific research: Economics and management, 8(3(28)), 243-245.
- Pryakhin, G. N., Trukhanov, D. A., & Maltsev, Yu. G. (2019b). Matematicheskaya model' delovogo uspekha organizatsii [Mathematical model of business success of an organization]. Mathematical and instrumental methods of Economics, 6(124), 15.
- Shamray, A. A. (2010). Zhiznennyy tsikl malogo predpriyatiya [Life cycle of a small enterprise]. Moscow: Liberal mission Foundation
- Strelchenko, E. (2019). High jewelry brand graff: key features of business strategy. Economic problems, 4, 143-146. https://doi.org/10.22394/2079-1690-2019-1-4-143-146
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
16 April 2021
Article Doi
eBook ISBN
978-1-80296-104-1
Publisher
European Publisher
Volume
105
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-1250
Subjects
Sustainable Development, Socio-Economic Systems, Competitiveness, Economy of Region, Human Development
Cite this article as:
Trukhanov, D., & Pryakhin, G. (2021). The Mathematical Structure Of Business Success. In E. Popov, V. Barkhatov, V. D. Pham, & D. Pletnev (Eds.), Competitiveness and the Development of Socio-Economic Systems, vol 105. European Proceedings of Social and Behavioural Sciences (pp. 331-338). European Publisher. https://doi.org/10.15405/epsbs.2021.04.36

