Figurative Thinking In Studyng And Teaching Fundamental Mathematical Concepts At School

Abstract

The article reveals the problem of applying figurative thinking in the process of studying the fundamental concepts of mathematical analysis. The fundamental concepts of mathematical analysis include: real number, function, limit of a function at a point, continuity of a function. The article reflects the content of student’s ideas about fundamental mathematical concepts of mathematical analysis, the possibility of actualization of student’s pre-scientific ideas. The regularities of development of pupil’s visual images of mathematical notions are specified. The findings are based on studies of students' ideas about mathematical concepts. The types of images of mathematical concepts are disclosed: geometric, symbolic, artistic. The essence of stages of formation of fundamental mathematical concepts is characterized: the stage of "worldly" representations, the stage of monomodal mathematical representations, the stage of complex representations, the conceptual stage, the conceptual stage. The possibilities of using various forms of mathematical notions' representation are specified. The schemes demonstrating the interrelation of mathematical concepts and ideas in a school mathematics course are given. At presentation of a theoretical material the picked up examples which illustrate use of figurative thinking of pupils at studying of fundamental concepts of the mathematical analysis in a course of mathematics are applied expediently.

Keywords: Fundamental mathematical conceptsmath educationquality math instructionunderstanding in teaching mathematics

Introduction

In didactics and psychology the theory of step-by-step formation of mental actions, which implements an operational approach to the formation of concepts, is developed. According to this theory, the learning of mathematical concepts takes place in the process of learning activities: summarizing under the concept; deducing the consequences; comparison; classification. The action is not assimilated if it is not carried out. Performing actions with features of concepts and serve as a tool for building a concept, its creation.

In addition to the operating room, there is an updated approach to the formation of concepts associated with the construction of an image that develops from the reflection of students' experienced ideas to higher degrees of abstraction. With this approach, the main attention is paid to the formation of associations of worldly ideas and previously acquired knowledge with new, subject to training.

Problem Statement

The formation of the concept of continuity of a function can be implemented through the construction of an association of geometric representations of this concept with an intuitive idea of the continuity of a curve — a line that can be moved with a free movement of the hand without taking the pencil from the paper. Among other mathematical facts, the images of which can be associated associatively in the students' minds, we give the following: the limit of the function in accuracy and the value of the function at the point, the argument of the function and the value of the function, the discontinuity of the function at the point and the continuity of the function at the point. These examples, firstly, do not exhaust all possible associations in the study of the fundamental concepts of mathematical analysis. Secondly, they illustrate only those associations that can be deliberately built in the learning process, and not at the first stage of cognition, but in the future. If these associations do not correspond to the mathematical meaning of the concept, then in the future this can lead to erroneous conclusions and incorrect generalizations. This will be manifested in errors in solving problems, difficulties in using this concept for the further construction of the theory.

In a stating experiment, high school students were offered the task of identifying associations with terms: aspiration, correspondence, change, dependence, movement (which mathematical concepts arise in association with these terms). If “correspondence” was associated with the concept of function by about 90% of people, then with the term “dependence” only 40% of students associate this concept. 60% found it difficult to answer. This example shows that the idea of dependence does not work, despite the fact that the term “dependence” is used in the definition of a function that is given in a school course.

Research Questions

The same conclusion is drawn by the fact that many schoolchildren have difficulty assigning tasks to construct functions that model some relationship between the quantities (physical, geometric, etc.) available in existing textbooks. The consequences of this are difficulties in solving the problems of using the derivative, to which the program in mathematics pays special attention.

The process of conscious study of fundamental mathematical concepts can be ensured based on the figurative component of thinking, which makes it possible to involve various forms of representing ideas in the formation of concepts. The role of imagery in the development of human intelligence is noted in philosophical, psychological and pedagogical scientific literature. An image is a subjective picture of the world or its fragments, including the subject himself, the spatial environment, the temporal sequence of events (Ganzen, 1974).

In training, images perform important functions that are reflected in the scientific and psychological literature (Correa & Guzmán-Franco, 2001; de Boer et al., 2018):

• acquisition, storage and reproduction of information;

• creating a proactive behavior program;

• reference function;

• regulation of actions.

Figurative thinking is an activity that provides the creation of images, operating them, transcoding them in a given or arbitrary order, using different reference systems to build images, highlighting various signs and significant properties in the image.

In the process of teaching fundamental mathematical concepts, figurative thinking is formed under the influence of two factors. Firstly, the content of concepts, conditions and forms of presentation of the facts to be studied. Secondly, the subjective selectivity of students, their propensity to work with the image, emotional attitude to knowable facts.

For a successful study of the beginnings of mathematical analysis, it is necessary for students to have a stock of initial, simplest images (specific functions: linear, quadratic, inverse proportionality; their graphs and properties) that carry information in various forms.

Visual images are divided into three types:

• geometric (graphic);

• sign-symbolic;

• art.

Purpose of the Study

Geometric images capture the properties of abstract objects, reflecting such as shape, size, spatial distribution. In mathematical analysis, such objects are a function, a sequence, a function limit, for which the geometric representation is most adequate. The ability to operate with graphic images is inherent in almost all students. This is confirmed by one of our ascertaining experiments, when even before a detailed study of the properties of functions, the concepts of limit and continuity, students were offered a task in which three function graphs were grouped. The functions given in each of the groups possessed one common property. Students were required to supplement each of these groups with a fourth function from a separate set. Most students (87%) completed the task correctly.

Sign-symbolic images reflect the common properties, operations and relationships inherent in ideal objects. The latter are characterized by a specific set of elements (numbers, letters, symbols, etc.), a designation of the relationship between them, their spatial distribution and mutual affiliation. This type of image plays an important role in the formation of the semiotic function of children (Snakov, 2005). The study of the fundamental concepts of mathematical analysis is associated with the formation of sign-symbolic images of analytical functions, function limits, etc. This type of images provides the ability to solve equations, inequalities, perform expression transformations, which is important in the study of mathematical analysis.

Artistic images are characterized by the ability to most fully reproduce the objectivity of the object, the whole variety of its features. The significance of the perceived object for the student’s personality when creating an artistic image is most important. When they study the fundamental concepts of mathematical analysis, this type of image contributes to the emotional and aesthetic perception of facts, which occurs due to the connection with any life situations, the involvement of historical material of interest to the student.

Research Methods

The study was carried out on the basis of a set of theoretical approaches and empirical methods, which made it possible to identify various approaches to the formation of mathematical concepts. Teaching methods were used: analysis of scientific literature on the problem of the formation of mathematical concepts, studying the experience of teaching mathematical analysis at school, organizing and conducting a stating experiment, and qualitatively processing its results.

Findings

It is possible to begin training in the fundamental concepts of mathematical analysis with the disclosure of the underlying concepts. Since it is difficult to achieve this by means of only analytical thinking, it is important that the image of the students be formed. At the first stage - a visual image, which subsequently develops to a conceptual one. At the same time, in order to understand each of the concepts, it is necessary for students to go through a series of stages that can be represented in the form of a diagram (Figure 1 ).

See Full Size >

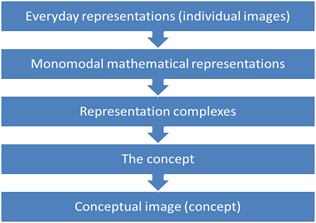
Let us characterize the essence of each of the stages in the formation of a fundamental mathematical concept.

• (A) Stage of everyday representations

Without attention to personally significant psychic formations - spontaneously formed pre-scientific “worldly” ideas, the possibility of organizing meaningful assimilation of concepts is unlikely, due to the lack of guarantees that the facts presented to the student’s attention will be accepted irrespective of their knowledge. In this regard, “everyday” ideas related to the terms of concepts are analyzed in order to determine their adequacy to the scientific meaning of concepts.

• (B) Stage of monomodal mathematical representations

At this stage, based on “everyday” ideas, the student is represented in the most adequate form by objects representing the scope of the concept. The choice of one form or another for the presentation of mathematical material at school is due to the compliance with two basic requirements. First, the presentation of the content should in the most vivid form reflect the essence of the concept being studied, that is, adequacy from a mathematical point of view is necessary. Secondly, this form should contribute to the development of the image of the concept, becoming the first step in understanding (Bahmutskij, 2012).

• (C) Integrated presentation phase

Images in which objects are reflected in the totality of their properties and relationships are called complex representations. In the framework of such representations, the student can move from the analysis of some properties of the object to the analysis of its other properties, showing flexibility in thinking.

• (D) Stage of monomodal mathematical representations

Based on the complexes of representations that reflect the properties of mathematical objects in various forms, the essential properties are distinguished. At this stage, definitions of concepts are given at the level of rigor that meets the learning objectives. Formal procedures for handling the concept are being worked out (Kuleshova & Brejtigam, 2019).

• (E) Conceptual phase

At this stage, a holistic content of the concept is formed, containing logical and intuitive components. The concept is not reduced to individual elements of representations, but is characterized by an awareness of meaning. This ensures that the concept is used to build another theory, to solve non-standard problems that require students to independently choose an adequate form of presentation of the concept, the optimal transfer of content from one form of presentation to another (Imai et al., 2016).

The implementation of the operational approach (Bloom, 1956) gives good results in the study of such concepts that:

• do not contradict the everyday ideas of students;

• have a first level of abstraction;

• are implemented within the same discipline;

• have an image expressed in one form.

The operational approach can be used, for example, in the study of the concepts of Euclidean geometry (Schrijvers et al., 2019). In the process of studying the fundamental concepts of mathematical analysis, the operational approach is applicable to the formation of concepts that play an auxiliary role. For example, interval, function argument, function increment at a point, etc.

When studying the fundamental concepts of mathematical analysis, such an approach (Kisel'nikov, 2010) is less suitable for obtaining the desired results. The reasons are as follows.

1. The knowledge of the concepts of number, function, limit and continuity of function is not limited to the framework of one school discipline. They are in the nature of meta-subjective concepts. Meta-subjective concepts are key fundamental objects that have their manifestation and problems in various academic disciplines (physics, chemistry, economics, history, and others, both natural and human sciences). Primary meaning is a key concept, category, phenomenon or other object that concentrates a fairly wide area of knowledge and goes beyond the scope of one discipline. Other examples of primary thinking are the categories of space, time, motion; concepts of letters, notes; elements of the world - fire, water, air, earth. We will also include the ideas of measurement, infinity, proximity, symmetry, change, aspiration, and dependence as primary ideas. These ideas are closely related to concepts (Figure 2 ).

See Full Size >

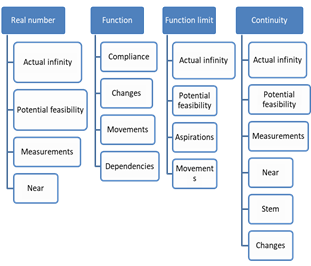
The process of learning the fundamental concepts of mathematical analysis can be constructed in such a way that it gives life to the ideas that underpin it. This will make it possible: to establish links between the concepts, ideas and concepts under study; to bring theory closer to the practice of its application. The possibility to involve worldly ideas in the learning of mathematical analysis, to build associations between these ideas and mathematical ideas in the operational approach is not considered. According to it, the concept can be considered assimilated by a student if he possesses essential properties and is able to use them in the process of operation. As a result of learning, the pupil should develop a knowledge system - a set of both basic and derived features of subjects we know of in the concept, as well as knowledge of what specific forms the elements contained in its volume exist. However, this does not exhaust the knowledge about the concept. Even when dealing with purely abstract objects, a person strives to introduce into his or her reasoning the elements of visibility, constructing for this purpose some notions - visual models of objects. These visual models allow making visible the ideas underlying the notion.

2. At studying of fundamental concepts of the mathematical analysis it is necessary to consider rich expressive possibilities which are available for their representation. Various forms can be used: verbal, sign-symbolic, graphic. No other section of mathematics studied at school has such a wide range of possibilities of representation. In order to illustrate the advantages of mathematical analysis in its fundamental part, it can be compared with the algebraic material studied at school (Figure 3 ).

See Full Size >

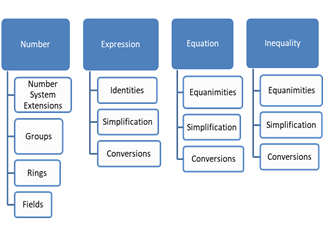
Firstly, most algebraic concepts and ideas do not have the nature of first thoughts. Secondly, the ideas accompanying algebraic concepts and facts are expressed mainly in sign-symbolic language. The difficulty in mastering this language, the impossibility of reinforcing it with a more accessible geometric pattern for students leads to the fact that the possibility of understanding the meaning of these ideas becomes real closer to the end of the study of the concepts of the course. Conditionally symbolic images of algebraic ideas are formed only on the basis of multiple transformations, operations. This is associated with the cost of training time. We have a fundamentally different picture when studying the fundamental concepts of mathematical analysis. The richness of expressive means for presenting his ideas, the lack of the need for preliminary assimilation of the operational side makes it possible to study them earlier - before acquaintance with the concept, at the very first stage. Moreover, the development of ideas comes earlier than the development of the full content of the concept. This creates the basis for understanding. it is precisely the ideas that are clearly presented that act as such a means for the student.

3. The everyday representations of students associated with the terms addiction, conformity, aspiration, limit, continuity, etc., formed at the time of studying the beginnings of mathematical analysis for the most part spontaneously, are characterized by blurry, fuzzy, incomplete on the one hand and individuality, personal significance - with another. the transition from everyday perceptions through the definition to the concept cannot be carried out according to the operating scheme, since the actions taken cannot be directly correlated with individual images. It is necessary to carry out preliminary work on bringing individual images to such a level when they will be characterized by clarity. Ignoring individual images, an early transition to abstractions leads to the formation of inadequate ideas in students, although the student demonstrates formal knowledge. For example, when solving inequality by the interval method, technical errors are made, the cause of which is the habit of determining the sign of a function at various intervals by direct substitution, while the method of analyzing sign changes is more reliable.

Students' representations perform an important function not only at the first stage of studying concepts, but also at the final stage: for application to solving applied problems, for use in non-standard situations (Podhodova, 2015). In the search for solutions to problems, when reasoning is conducted blindly, by touch, it is not known which of them will be needed to solve, success provides possession of representations of content in various forms. The flexibility of thinking is ensured by the complexes of representations containing information about the concept in verbal, graphic, sign-symbolic forms, which allow translating content from one form to another (Mullis & Martin, 2017; Weinberg, 2017).

Conclusion

The study of the use of imaginative thinking in the study of the fundamental concepts of mathematical analysis in the school course of mathematics allows us to draw the following conclusions.

• A. Concepts are formed in stages

The formation of fundamental concepts of mathematical analysis can be carried out on the basis of updating intuitive representations, and later on, gradually improving the images of these concepts (from reflection in representations of mathematical content expressed in one form to a complex representation in various forms, and from it to a holistic conceptual representation). In the learning process, the student must go through a series of stages from worldly representations to conceptual understanding.

• B. In the process of forming concepts, content is translated into various languages of representation

The need for students to develop flexible thinking, which is based on complexes of representations of the content of the fundamental concepts of mathematical analysis, is the reason for special consideration of the translation of mathematical content into various presentation languages.

• C. For the formation of concepts using special methodological tools

An analysis of the scientific psychological and pedagogical literature concerning the problem of the formation of mathematical concepts leads to the realization of the need to choose methodological tools for the formation of integral images of the fundamental concepts of mathematical analysis. Such a tool can be special tasks, tasks and exercises.

• D. The formation of fundamental mathematical concepts is based on the imaginative thinking of students

It is possible to attract means of imaginative thinking to the formation of the fundamental concepts of mathematical analysis. The following is fixed in the images: the ideological meaning, due to which the concept is operated consciously, applied to solve non-standard problems, and subjectively processed experience. It is impossible to create and hold an image, let alone operate in an image to the content of which the subject is indifferent.

References

1. Bahmutskij, A. E. (2012). The content of the results of general education and the activities of teachers. Izvestiya RSPU im. A.I. Herzen, 148.
2. Bloom, B. A. (1956). Taxonomy of Educational Objectives, Handboor 1: Cognitive Domain. David Mc Kay.
3. Correa, R. I., & Guzmán-Franco, M. (2001). Maestros: de la tiza al bit. Comunicar, 16, 181-187. https://doi.org/10.3916/C16-2001-25.
4. de Boer, H., Donker, A. S., Kostons, D. D. N. M., & van der Werf, G. P. C. (2018). Long-term effects of metacognitive strategy instruction on student academic performance: A meta-analysis. Educational Research Review, 24.
5. Ganzen, V. A. (1974) Perception of Holistic Objects. Leningrad.
6. Imai, M., Kanero, J., & Masuda, T. (2016). The relation between language, culture, and thought. Current Opinion in Psychology, 8, 70–77. https://doi.org/10.1016/j.copsyc.2015.10.011
7. Kisel'nikov, I. V. (2010). The process approach to ensuring the quality of teaching mathematics in a comprehensive school. The World of Science, Culture, Education: A Scientific Journal, 1.
8. Kuleshova, I. G., & Brejtigam, E. K. (2019). The contents of the phases of understanding of the educational material. Scene for Education Todai, 5.
9. Mullis, I. V. S., & Martin, M. O. (Eds.) (2017). TIMSS 2019 Assessment Frameworks. Boston College, TIMSS & PIRLS International Study Center website. http://timssandpirls.bc.edu/timss2019/frameworks/
10. Podhodova, N. S. (2015). Understanding in Teaching in Mathematics: Necessary Conditions for Achieving “68 Herzen Readings”: on the 95th Anniversary of the Department of Teaching Methods in Mathematics and Computer Science. Russian State Pedagogical University named after A.I. Herzen.
11. Schrijvers, М., Janssen, Т., Fialho, О., & Rijlaarsdam, G. (2019). Gaining insight into human nature: a review of literature classroom intervention studies. Review of Educational Research, 89, 1. https://doi.org/10.3102%2F0034654318812914
12. Snakov, V. V. (2005). The Psychology of Understanding: Problems of Perspective. Publishing House "Institute of Psychology RAS".
13. Weinberg, P. J. (2017). Supporting Mechanistic Reasoning in Domain-Specific Contexts. Journal of Pre-College Engineering Education Research (J-PEER), 7(2), 3. https://doi.org/10.7771/2157-9288.1127