The Influence Of The Population Distribution System On Regional Development

Review of previous studies

Zipf proposed a formalized theory using the ratio “rank-size”, which shows the optimal distribution of the population by settlements (Zipf, 1949). His formula found application in the analysis of population distribution systems at the global, national, regional and even intracity levels (Friesen, Taubenböck, Wurm, & Pelz, 2018). Using Zipf’s law, an analysis was made of the population distribution system of many states, for example, Russia (Rusanovskiy, Markov, & Brovkova, 2018), Poland (Cieslik & Teresiński, 2017), USA (Devadoss, & Luckstead, 2016), Brazil (Chauvin, Glaeser, Ma, & Tobio, 2017), Mexico (Pérez-Campuzano, Guzmán-Vargas, & Angulo-Brown, 2015), China (Farrell & Nijkamp, 2019), India (Luckstead & Devadoss, 2014), Pakistan (Arshad, Hu, & Ashraf, 2019) and others.

In some works, it was found that Zipf's law works best when studying objects distinguished not by administrative, but by functional boundaries (Veneri, 2016). The “rank-size” pattern is used when analyzing the distribution of not only the population, but also other indicators, for example, employment (Tsekeris, 2019), firms (Bee, Riccaboni, & Schiavo, 2017), etc.

Alternative approaches to assessing the degree of balance of the population distribution system

As an approach to revealing the spatial balance of the population distribution system, not only Zipf's law can be applied, but also the Lorentz curve, Gini coefficient (Farrell & Nijkamp, 2019), the Herfindahl-Hirschman index, the calculations of Christaller, Losch, etc. Zipf's law can be used in combination with other spatial patterns, for example, the distance between cities (González-Val, 2019).

Research hypothesis

The hypothesis of the study is the connection between the pace of development of the region and the balance of the population distribution system. The annual growth rate of GRP (Gross Regional Product) per capita at the prices of the previous year is used as an indicator characterizing the economy of the region. The Zipf's coefficient is used to characterize the degree of balance of the population distribution system.

The concentration of the population can have both positive and negative effects. For example, with concentration, an agglomeration effect occurs, which accelerates development compared to a uniform distribution of the population. However, excessive concentration can lead to the emergence of a agglomeration diseconomies, which is the opposite of the agglomeration effect, which will ultimately undermine the competitive advantages over the even distribution of the population. Of course, the balance of the population distribution system does not determine the development of the region by 100%, because there are many other factors. In addition, the degree of influence of the population distribution system is due to the geographical and economic connectivity of the settlements within this system.

Study Assumptions

The following assumptions were made as part of the study:

• Cities or another settlements are usually accepted as elements of a population distribution system. In this study, instead of settlements, local administrative unit (which called municipalities) of the first level (they are not included in other municipalities) were investigated: urban districts and municipal areas. Within municipal areas there are several lower-level municipalities (e.g. urban settlements, rural settlements). In this study, such a high level of detail of the population distribution system was not carried out, confining itself to first-level municipalities.

• Municipalities were considered within their administrative boundaries. However, in reality, some administrative units form a single socio-economic system, their built-up territories are combined, as a result of which an agglomeration is formed. Therefore, it would be more logical to consider some integrated municipalities as a single municipality (as an agglomeration). However, in Russia there are no statistics on agglomerations.

• As an indicator characterizing the development of the region, the annual growth rate of GRP per capita at the prices of the previous year was taken. An alternative indicator could be labor productivity, average monthly wages, etc.

Zipf’s law, other methods and data sources

Zipf's law is described by the formula (1):

$P_n=\frac{P_1}{n}$ (1)

where P_n– optimal population of a city with a rank “n”; P₁ – population of the largest city of this population distribution system.

Note that there are more complex interpretations of Zipf's law, for example, in the form of constructing a linear regression dependence between the decimal logarithm of the actual population and the logarithm of rank (Zipf, 1949; Andreev, Lukiyanova, & Kadyshev, 2018):

$lgN=A+a*lgR$ (2)

where N – population of a city with a rank “R”; R – rank; a – Zipf's coefficient; A – constant.

If $\left|a\right|>1$, then there is a concentration of the population in large cities. If $\left|a\right|<1$, then there is a concentration of the population in medium and small cities. The constant “A” shows the target population of the largest city to approximate the distribution according to Zipf's law (when “a” equals “-1”).

The study uses regression, correlation and comparative analyzes. The source of statistical information was the website of the Federal State Statistic Service of Russia (Federal State Statistic Servi…, 2018).

Object of study

In Russia, it is possible to distinguish the following population distribution systems: at the local level, subregional (part of the region), regional, at the level of the federal district (several regions), at the state. However, within the state and the federal district, the institutional conditions are uneven: regional policy, the volume of transfers from the federal center, and so on are different. Therefore, it would be logical to conduct an assessment at the regional level. The object of research is the Samara region. The analyzed period: 2010-2018.

It is important to answer the question about the sample of settlements within the region. In paragraph 2.2. it has already been said that first level municipalities were taken. When applying the Zipf's law, there are different approaches to sampling:

• A mixed sample of first-level municipalities (urban districts) and second-level municipalities (urban settlements). Those. those municipalities that are conditionally referred to as “cities” are selected. Sometimes a selection is added according to the criterion “population” (for example, cities with 100 thousand people are selected);

• A mixed sample of first-level municipalities (urban districts) and second-level municipalities (urban settlements, rural settlements);

• In this study, an alternative approach is used: only the municipalities of the first level (urban districts and municipal areas) are analyzed. Such a sample will cover 100% of the region’s population, and it is not necessary to collect statistics on small rural settlements in municipal areas.

In the Samara's region there are 37 first-level municipalities (which are not included in any other municipalities): 10 urban districts, one of which is an urban district with intracity division, 27 municipal districts. Samara as an urban district with intracity division includes 9 intracity districts (municipalities of the second level). Within 27 municipal districts there are 296 municipalities of the second level: 12 urban settlements and 284 rural settlements. I.e. total 305 municipalities of the second level (Government of the Samara's region, 2018).

Description of the research object

The population of the Samara's region at the beginning of 2018 is 3193514 people who are accomodate in 37 first-level municipalities (Table 01 ).

Perfect share according to Zipf's law, actual share of municipalities in the region’s population

It is necessary to compare the actual distribution with the perfect. The perfect share was found as follows (Table 02 & Table 03 ):

• It is suggested that a city with a rank “1” already has a perfect population (in step 5, this assumption is reviewed);

• Perfect population can be found for all other municipalities: the rank is known for all municipalities, so formula (1) can be used;

• The total perfect population of all municipalities is found (through summation);

• The perfect share of each municipality from the total perfect population is found;

• Based on the actual total population of all municipalities and the known perfect share of each municipality, we can find the perfect population of each municipality (taking into account of the actual total population).

All 37 municipalities of the Samara's region are divided into 3 approximately equal groups (12, 12, 13 municipalities). Each group can be conditionally classified taking into account the population as relatively large, relatively medium, relatively small. For a real example of the Samara's region, the perfect shares are shown in Table 03 (Table 03 ). These values, when they are rounded to the nearest hundredth, are relevant for each year from the period 2010-2018.

Table 04 shows the actual shares of each group (Table 04 ).

Thus, the actual share of large municipalities in 2018 is 83.26% (Table 04 ), which is almost 10% higher than the perfect share of 73.86%. Based on the fact that, according to Zipf’s law, the perfect shares of each municipality are known, it is possible to construct a graph showing the actual and perfect distribution of the population (Figure 01 ).

See Full Size >

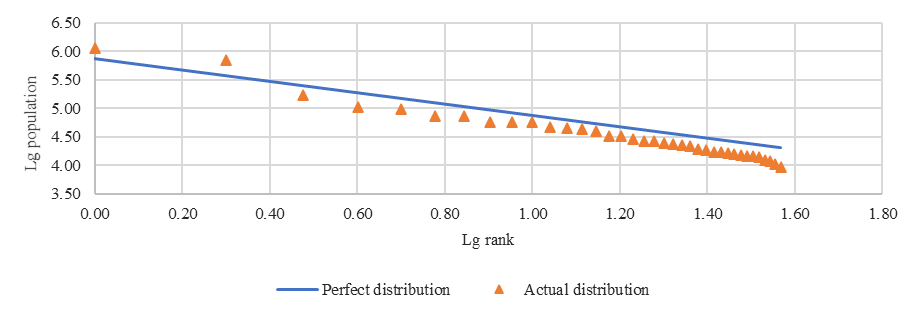
From Figure 01 it can be seen that only two municipalities in the Samara Region have a population higher than the recommended one; all other municipalities have a shortage of population, which makes the system unbalanced.

Figure 02 shows a graph of the actual and perfect distribution of the population for 2010 (Figure 02 ).

See Full Size >

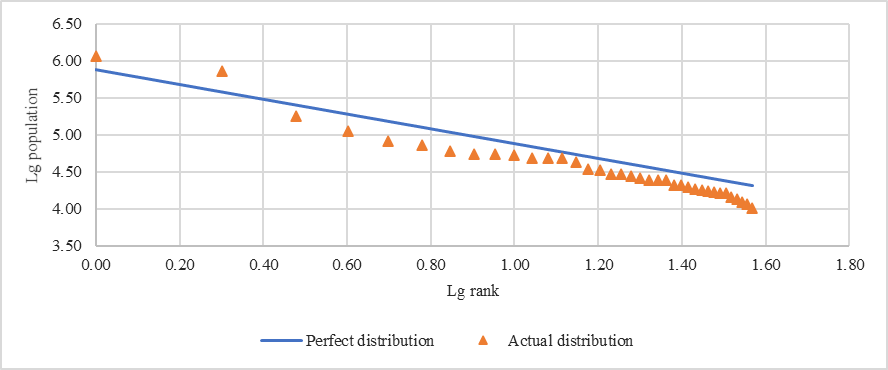
We apply formula (2) to find the parameters of the regression equation that reflects the population distribution according to Zipf's law for the Samara region (Table 05 ). A regression equation is constructed in which “x” are the logarithms of the ranks, “y” are the logarithms of the population.

The regression equation is obtained according to the Zipf’s law for 2018 (3):

$lgN=\mathrm{5,94}-\mathrm{1,203}*lgR$ (3)

The dynamics of the Zipf's coefficient “a” for the period 2010-2018 years shows its growth, which suggests that relatively large municipalities have increased their share in the population. This is consistent with the data in Table 04 (population growth in the group of the first 12 municipalities). The population distribution system of the Samara's region is becoming increasingly unbalanced with a shift to the dominance of large municipalities.

The visual analysis of Figures 01 and 02 gives the impression that the actual distribution of the population in 2018 compared to 2010 has approached the perfect level. However, calculations show that in 2018, compared with 2010, the deviation of the actual share in the population from the perfect increased in 30 of the 37 municipalities of the Samara's region. So the population distribution system as a whole has become truly less balanced.

The impact of the population distribution system balance on the pace of development of the region

It is necessary to find out whether there is a functional relationship between the balance of the population distribution system and the annual growth rate of GRP per capita in the prices of the previous year. The Zipf coefficient “a” acts as a factor variable, and the rate of change in GRP as the resulting variable (Table 06 ).

The obtained linear regression equation is shown in formula (4):

$\left(AnnualgrowthrateofGRPpercapita\right)=\mathrm{4,49}+\mathrm{2,93}*а$ (4)

The p-value criterion shows that the equation is significant with a probability of more than 99%. The determination coefficient R² is 0.81; 81% of the variation in the rate of development depends on the variation of the population distribution system.

There is a negative functional relationship: the greater the imbalance in the population distribution system according to Zipf's law, the lower the growth rate of GRP per capita per year.

Evaluation of the statistical relationship gives similar results: the correlation coefficient “r” is 0.90; the statistical relationship is strong (in the range of 0.7-0.9); with (8-2) = 6 degrees of freedom, the actual value of the correlation exceeds the critical value of 0.834 with a significance level of 99%. The connection is negative: the stronger the unbalanced system, the lower the pace of development of the region.