Abstract
Practice demands, on the one hand, and new opportunities offered by development of digital economy, on the other hand, raise the issue of requirement for increasingly more efficient methods of managing complex manufacturing systems. One of characteristic features of the latter is the versatility and variability of goals and criteria due to continuously changing external and internal environment. The multicriteriality problem has many aspects. The paper is dedicated to one of them, namely: development of the methodology for building and using dynamically changing multi-level vector criteria for optimization of engineering and manufacturing complexes. The approach applied most frequently involves vector to scalar conversion of the optimization criterion. When multi-level criteria are used we have to deal with a system of embedded convolutions forming a hierarchical system of vectors. The current principles of making convolutions for such systems can be implemented in different ways depending on peculiarities of the controlled object and management goals. This study discusses building of hierarchical criteria in mathematical setting up of engineering and manufacturing complex optimization problems. A method of forming and scalarization of a hierarchical vector criterion following a recurrent procedure based on an invariant representing a linear combination of Holder norms of partial criteria is suggested.
Keywords: Management of engineering and manufacturing complexesdynamically changing prioritiesgoal programmingvector optimizationhierarchical criteriaconvolutions of vector hierarchical criteria
Introduction
Management of engineering and manufacturing complexes is associated with the vector optimization problem. The orthodox approach according to which the management goal is characterized by one index and conditions – by multiple rigid restrictions prohibiting any violations falls short in real life today (Caballero, Romero, & Ruiz, 2016). Improvement of the economic status and the level of innovative development of enterprises might be implemented only based on application of a multi-criterial vector optimization and building a systemic-hierarchical model comprising about ten integral groups of indices (Yashin & Soldatova, 2013).
Most available methods, especially when we are talking about optimization, involve vector criterion scalarization. At first, all input partial criteria are reduced to a comparable dimensionless form, normalized relative to some reference or plan values. Then, the normalized values, taking into account weight coefficients showing their importance, are convoluted according to some formula and the result obtained is regarded as a generalized criterion of optimization. In practice, the goal programming method is the most common. It consists in usage of convolution that is some measure of a distance from the vector estimate under analysis to some target value.
In forming and scalarization of multi- level criteria, hierarchical decomposition (MCHP) is used, which should be considered the basic methodology (Corrente, Doumpos, Greco, Słowiński, & Zopounidis, 2017; Colapinto, Jayaraman, & Marsiglio, 2017).
There are two aspects of the scalarization problem. The first aspect consists in evaluation of priorities. The most constructive approach is to form intuitive peer estimates and their processing with the help of fuzzy interval mathematics (Akram & Shahzadi, 2018; Corrente, Greco, & Slowinski, 2017). The second aspect is caused by the necessity of performing a sequence of procedures to calculate intermediate convolutions. Generation of solution variants and their evaluation based on the vector criterion convolution are separated. Therefore, various randomized heuristics have to be applied to solve multi-criterial optimization problems (Shvarc, 2013; Tomashevsky, 2017). These are most often genetic and evolution algorithms (Ke, Deb, Zhang, & Kwong, 2015; Kalyanmoy & Himanshu, 2014).
Adaptive systems of dynamic management of complex objects (Lopez & Lewis, 2018) have been intensively developed recently, as well as systems centered on the concept of combining intellectual capabilities of a human being and computer faculties in an optimal way. Wesner (2017) described a system of multi-goal optimization wherein interactive methods of Pareto region visualization are utilized. The task of a computer is to present information so that it would be convenient for a decision-maker to make a choice based on his experience and intuition. The heuristic solving algorithm is included in the system only as an additional option.
Problem Statement
Optimization of an engineering and manufacturing complex is a large, in terms of the number of dimensions, intricate problem. It is impossible to solve it with the help of some algorithm where the procedure of forming a solution variant and the procedure of its evaluation are separated. In this instance, calculation of multi-level criterion convolution by performing a sequence of intermediate convolutions is not appropriate. The task of this study is to present the hierarchical criterion in a form allowing its integration into a mathematical programming problem.
Research Questions
Within the MCHP methodology, Voronin (2007, 2017) has suggested a method of criterion synthesis by forming embedded convolutions making up a hierarchical system of vectors:
(1)
where is the vector of criteria of the -the level engaged in formation of estimates at the -the level; is the number of levels; is the number of estimated attributes of the -the level.
In the estimation of -the attribute of the -the level, each component of the -the level criterion is assigned some index of significance (importance) that is characterized by a respective priority coefficient. The set of such coefficients makes up a system of priority vectors:
(2)
The criterion is formed so that vector criteria of a higher level are formed from convolutions of components of lower level criteria. Thus, one gets that the generalized criterion is nothing but a scalar convolution obtained for the higher level.
The generalized criterion is built through some recurrent procedure that represents a sequence of operations of convolution of vector criteria of each level starting from the lowest, taking into account the priority vectors:
(3)
The methodology allows many implementations. The main question in solving the postulated problem is instantiation of the operator (3).
Purpose of the Study
The purpose of this study is to develop a methodology for forming and using hierarchical vector criteria to optimize engineering and manufacturing complexes, including 1) building a hierarchical vector criterion, 2) forming its convolution, 3) integrating into a linear optimization problem.
Research Methods
The task of multi-criteria optimization of some manufacturing and economic system will be thought of as
(4)
where is the vector of controlling variables; is the vector of target indices; is the matrix of linear conversion of the vector of variables into the vector of indices; is the matrix of engineering and manufacturing parameters; is the vector of engineering and manufacturing constraints; is the vector of weighted relative deviations of the calculated values of indices from prescribed values; is the diagonal matrix, the elements of which are priorities of indices; is a unity matrix; is some convolution.
In this instance, the hierarchical criterion is formed when target indices included in the problem are grouped and subgrouped at several levels. The result is a treegraph with number of levels. Its leaves are components of vector . Intermediate nodes of the graph are criteria corresponding to groups and subgroups.
Investigations undertaken by the author have shown that convolutions are formed best of all with the help of a recurrent formula representing a convex linear combination of Holder norms of the first and infinite orders:
, (5)
where is the -th criterion of the -th level; is the set of criteria of the -the level involved in formation of the -the criterion of the -the level; is the priority of the -th criterion of the -the level; is the tunable parameter of convolution; .
Criteria ranking can be done in one of the two ways. The first one is assigning priorities directly; the second is ranking based on their paired comparison. In the second case, priorities are then determined as eigenvalues of the matrix of paired comparisons.
In every compartment of every level, priorities, regardless of the way they have been obtained, are normalized so that their sum would be equal to unity, which is essential in the formation of a multi-level criterion. In each compartment of each level, priorities of making them up criteria are determined only relative to each other. The priority of the compartment itself is formed in the group of criteria of the next level.
As the objective function of the problem, the convolution corresponding to the root node of the graph - - is used. In this case, to get the root convolution there is no need to perform the sequence of operations (5) for all levels starting from the lowest. The final and intermediate convolutions are determined through the system of additional equations and inequations that are input into the matrix of initial problem conditions:
(6)
where is the set of criteria of the -the level; .
The criteria formation invariance is reflected on the structure of the block of additional constraints. Criterion is determined through underlying criteria by adding the next block of conditions.
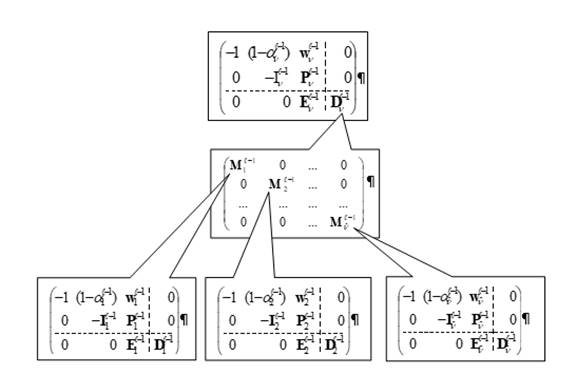
, (7)
where is the vector of weight coefficients; is the column of unities; is the diagonal matrix, the elements of which are priorities ; is the vector of criteria from which convolution is formed; are components of convolutions involved in forming vector ; and are block-diagonal matrices.
Diagonal blocks of matrix are columns . This matrix links the current matrix with daughter matrices that are input to form criteria of the underlying level and are diagonal blocks of matrix . Let us denote elements of set by sequence numbers , where ; we can write
, (8)
. (9)
As we see, the structure of daughter matrices fully matches the structure of the parent matrix. Matrices
are a structural matrix invariant and a kind of building blocks. The hierarchy of these blocks repeats the hierarchy of the criterion (Figure
Findings
1. An approach is presented that allows reducing formation of the vector criterion convolution and tuning of regulated parameters to a unified procedure. Tuning of parameters in each compartment of each level is determined separately, independently on others, allowing usage of different methods to estimate and rank input and intermediate criteria.
2. Determination of the root convolution of hierarchical criterion does not require to perform the sequence of calculations of intermediate convolutions from lower levels to the highest level. The root convolution is determined with the help of a system of linear relations input directly into the matrix of optimization problem conditions.
3. The hierarchical vector criterion is integrated into the matrix of conditions as a system of embedded into each other structurally similar matrices – matrix invariants.
Conclusion
A methodology of synthesis of hierarchical vector criteria in the problems of optimization of engineering and manufacturing complexes has been suggested. A recurrent procedure of hierarchical vector criterion scalarization and a method of its integration into the matrix of linear optimization problem conditions have been developed. The methodology has been used in the development of domain-specific software for systemic multi-criteria optimization of oil refinery (Livshits & Sizikov, 2016).
References
- Akram, M., & Shahzadi, S. (2018). Novel intuitionistic fuzzy soft multiple-attribute decision-making methods. Neural Computing and Applications, 29(7), 435-447. https://doi.org/10.1007/s00521-016-2543-x
- Caballero, R., Romero, C., & Ruiz, F. (2016). Multiple criteria decision making and economics: An introduction. Annals of Operations Research, 245(1-2), 1-5. https://doi.org/ 10.1007/s10479-016-2287-0
- Colapinto, C., Jayaraman, R., & Marsiglio, S. (2017). Multi-criteria decision analysis with goal programming in engineering, management and social sciences: A state-of-the art review. Annals of Operations Research, 251(1-2), 7-40. https://doi.org/10.1007/s10479-015-1829-1
- Corrente, S., Doumpos, M., Greco, S., Słowiński, R., & Zopounidis, C. (2017). Multiple criteria hierarchy process for sorting problems based on ordinal regression with additive value functions. Annals of Operations Research, 251(1-2), 117-139. https://doi.org/10.1007/s10479-015-1898-1
- Corrente, S., Greco, S., & Slowinski, R. (2017). Handling imprecise evaluations in multiple criteria decision aiding and robust ordinal regression by n-point intervals. Fuzzy Optimization and Decision Making, 16(2), 127-157. https://doi.org/10.1007/s10700-016-9244-x
- Kalyanmoy, D., & Himanshu, J. (2014). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 18(4), 577-601. https://doi.org/10.1109/TEVC.2013.2281535
- Ke, L., Deb, K., Zhang, Q., & Kwong, S. (2015). An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Transactions on Evolutionary Computation, 19(5), 694-716. https://doi.org/ 10.1109/TEVC.2014.2373386
- Livshits, M. Yu., & Sizikov, A. P. (2016). Multi-criteria optimization of refinery. In G.V. Kuznetsov, P.A. Strizhak, A.O. Zhdanova & E.E. Bulba (Eds.), Thermophysical Basis of Energy Technologies 2015 EPJ Web of Conferences, 110, (01035). Les Ulis Cedex: EDP Sciences. https://doi.org/ 10.1051/ epjconf / 201611001035
- Lopez, V. G., & Lewis, F. L. (2018). Dynamic multiobjective control for continuous-time systems using reinforcement klearning. IEEE Transactions on Automatic Control, 64(7), 2869-2874. https://doi.org/10.1109/TAC.2018.2869462
- Shvarc, D. T. (2013). Interactive methods for solving multi-objective optimization problem. Review. Science and Education, 4, 245-264 [in Rus.]. https://doi.org/10.7463/0413.0547747
- Tomashevsky, I. L. (2017). Multi-criteria optimization with logic interaction of criteria and alternatives. Economics and Mathematical Methods, 53(4), 105-113. [in Rus.].
- Voronin, A. N. (2007). A method of multicriteria evaluation and optimization of hierarchical systems. Cybernetics and Systems Analysis, 43(3), 384-390. https://doi.org/10.1007/s10559-007-0060-8
- Voronin, A. N. (2017). Multi-criteria decision making for the management of complex systems. Pennsylvania, USA: IGI Global. https://doi.org/10.4018/978-1-5225-2509-7.ch003
- Wesner, N. (2017). Multiobjective optimization via visualization. Economics Bulletin, 37(2), 1226-1233.
- Yashin, S. N., & Soldatova, Yu. S. (2013). Assessment of the economic status and the level of innovative development of enterprises based on the method of multi-criteria vector optimization. Finance and Credit, 19 (4(532)), 29-36. [in Rus.].
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
09 March 2020
Article Doi
eBook ISBN
978-1-80296-078-5
Publisher
European Publisher
Volume
79
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-1576
Subjects
Business, business ethics, social responsibility, innovation, ethical issues, scientific developments, technological developments
Cite this article as:
Sizikov*, A. P. (2020). Management Of Industrial Complexes Based On Dynamically Changing Multi-Level Criteria. In S. I. Ashmarina, & V. V. Mantulenko (Eds.), Global Challenges and Prospects of the Modern Economic Development, vol 79. European Proceedings of Social and Behavioural Sciences (pp. 578-584). European Publisher. https://doi.org/10.15405/epsbs.2020.03.83
