Mathematical Modeling Of Information Security Risks Inherent In Using Blockchain Technology

Abstract

A primary technology underpinning the creation and operation of the digital economy is blockchain or, more precisely, distributed ledger technology (DLT). The main reason for implementing blockchain in businesses is streamlining business processes by restructuring them to enhance their efficiency. Today the leaders in implementing DLT are the finance, energy, retail, and public sectors. These sectors all face the important problem of making the interaction between business processes transparent. Although it is being actively implemented and used in various industries, the technology has its shortcomings – information security risks involved in its use: the low performance of block network nodes; complicated network scalability; lack of legal regulation creates a threat to the blockchain environment; large amount of data stored on the network and problems relating to block network manageability and data confidentiality. The main cause of these shortcomings is that blockchain is decentralized. Thus, the main advantage of the technology also gives rise to a whole array of information security risks that need to be addressed. To form theoretical foundations for identifying information security risks, it is necessary to formulate basic approaches to creating fuzzy measuring scales and determine fuzzy operations on object sets, a list of membership functions, operations on linguistic values, and fuzzification and defuzzification functions.

Keywords: Digital economyblockchaininformation risksfuzzy measuring scalesmembership functions

Introduction

When identifying information security risks, one should use the fuzzy-inference mechanism. This mechanism combines the basic concepts of fuzzy-set theory: membership functions, fuzzy operations, fuzzy implication and composition, and linguistic variables. Thus, the use of this mechanism is a comprehensive approach to identifying information security risks, since it allows one to factor in the degree of the quality of assessing how effective the security of information resources is (using the associated fuzzy scale); the required level of protection; and the logical-inference rules that determine the level of information security risk.

Problem Statement

First of all, forming the model requires determining a fuzzy set of objects and assigning associated membership functions for each variable x ∈ X from that set. The form of a specific membership function μ ( x ) depends on the application environment in which the model under study operates ( Luo & Hu, 2016). Also influencing the type of function are various additional assumptions about its properties such as monotonicity, symmetry, and continuity of the first derivative ( Masneva & Petrushova, 2016). Here, the requirement that membership functions be continuous must be taken into account. When solving practical problems for forming an object model, one can know the values taken on by the membership function on the set x ∈ X . Endpoint data make it possible to represent the membership function as an approximating function.

Constructing the membership function involves using restrictions based on information about the functioning of the model. Most practical tasks are characterized by many criteria that can impose restrictions on the membership function, and this dictates the use of generalized indicators ( Korablev, 2016). We will form a set of eight fuzzy measuring scales to assess the components of the model: confidentiality, integrity, availability, value, impact, vulnerability of external borders, risk, and loss. For each scale, we need to provide a specific description and calculate the membership functions for fuzzy values.

When constructing the membership functions, we used carriers consistent with Harrington’s desirability function. The intersection of the carriers is determined by a value of 0.08 or ± 0.04 from the center of the common part. We limit the measuring scales to the segment [0,1], where 0 is the minimal level and 1 is the maximal level for the scale ( Geras’kin & Chkhartishvili, 2017).

The required level of information security risk depends on the type of membership function. The trapezoidal and triangular functions meet the most stringent requirements. The confidentiality scale of information blocks, S c o n f , is a fuzzy measuring scale that indicates the levels of confidentiality. The scale can be used to characterize the confidentiality property for model components.

Values for membership functions:

S c o n f 1 = 0 ; 0,24 , μ 1 x = μ s c o n f 0 ; 0,24 ; 0 ; 0,2 ;

S c o n f 2 = 0,16 ; 0,41 , μ 2 x = μ s c o n f 0,16 ; 0,41 ; 0,2 ; 0,37

S c o n f 3 = 0,33 ; 0,67 , μ 3 x = μ s c o n f 0,33 ; 0,67 ; 0,37 ; 0,63

S c o n f 4 = 0,59 ; 0,84 , μ 4 x = μ s c o n f 0,59 ; 0,84 ; 0,63 ; 0,8

S c o n f 5 = 0,76 ; 1 , μ 5 x = μ s c o n f 0,76 ; 1 ; 0,8 ; 1

The integrity level of information blocks, S c o n t , is a fuzzy measuring scale that indicates the levels of data integrity. The scale can be used to characterize the integrity property for model components. The scale of availability of information blocks, S i m p l e m e n t , is a fuzzy measuring scale that indicates the levels of availability of an information resource. The scale can be used to characterize the availability property for model components.

The value scale of information blocks, S v a l u e , is a fuzzy measuring scale that indicates criticality levels, making it possible to correlate protected information with the qualitative category characterizing it. The magnitude of potential loss depends on how valuable protected information is: the higher the value of the information, the greater the loss.

The scale of external influence on information blocks, S e f f e c t , which is a fuzzy measuring scale that indicates the levels of effects that model components have on one another, characterizes a fuzzy dependence on the occurrence of the threat ( Korablev, Petrushova, Pogorelova, & Abrosimov, 2019).

The vulnerability assessment scale for the outer boundaries of the DLT register, S v u l n e r , is a fuzzy measuring scale that indicates vulnerability occurrence levels. This scale is used because of the nuances of the application environment under study – the features of the distributed register. Using the developed scale and collected data, we need to assess the boundaries of the network nodes in relation to external threats. The loss scale of information blocks, S l o s s , is a fuzzy measuring scale that indicates loss levels. The scale is designed to assess the magnitude of loss and characterizes the fuzzy relation of model components to one another. The resulting fuzzy value needs to be defuzzified on the scale S l o s s = [0,1]. This set of scales should be considered a minimum for the investigated model of using blockchain technology.

Research Questions

The efficiency of information protection is related to the level of probability of an information threat occurring, which depends on the potential of the source of the security threat for the related vulnerability.

Presented in the form of inference rules below are the data showing the relationship between the potential of the source of the security threat and the related vulnerability:

(1) I F A i j < B i j T O P i j = 0

(2) I F A i j = B i j T O P i j = 0,5

(3) I F A i j > B i j T O P i j = A i j - B i j

where A i j is the threat level of protected information for the related j th vulnerability coming from the i th source; B i j is the value of the effectiveness of protecting information from the i th source exploiting the j th vulnerability; P i j is the probability of the occurrence of the threat coming from the i th source, which exploits the j th vulnerability.

Rule ( 1 ) is that the probability of a remote attack occurring will be negligible if the potential of the threat source is less than the level of protection effectiveness.

Rule ( 2 ) establishes equal probabilities of a remote attack occurring and of protection against it if there is equality between the potential of the threat source and the level of protection effectiveness.

The logic of rule ( 3 ) is that if the potential of the threat source is greater than the level of protection effectiveness, then the probability of a remote attack occurring will depend on how much the potential of the threat source exceeds the level of protection effectiveness.

According to the calculated probability of the threat occurring, it is necessary to determine the degree of the negative impact for the protected information ( Geras’kin, 2018). The degree of impact is the result, in the form of loss value, of the threat to protected information occurring in relation to the associated vulnerability of the information system. Input data for impact analysis are the value of protected information and its criticality.

We define the criticality property as the degree of importance of information about the tools and methods for providing information security that protect the company’s principal (critical) business processes. If it occurs, a threat that exploits the vulnerability in question leads to the loss of confidentiality, availability, and integrity of protected information resources ( De Gusmão, Silva, Silva, Poleto, & Costa, 2016).

Loss caused by information security risks can be quantified, for example, by the amount of lost profits or the costs of restoring lost data. There is also an approach to qualitatively assessing loss based on the use of an impact scale. Let us look at the advantages and disadvantages of the approaches to assessing information impacts ( Groumpos, 2016). The uncertainty inherent in the approaches requires analyzing additional information. That information may include the frequency of and costs resulting from the vulnerability as well as weight factors. The cost of vulnerability and the frequency of its occurrence under the influence of a specific threat to protected information are determined for a specific period. Information security risks are assessable with a method consisting in the pairwise multiplying of probabilities of the threat to protected information occurring by the magnitude of the loss caused by the threat ( Galbusera & Giannopoulos, 2018). The products then need to be ranked. This technique is recommended in National Institute of Standards and Technology Special Publication 800-39 NIST SP 800-39 and British Standards Institute Code of Practice for Information Security Management BS 7799 (ISO 17799) (2019), the only difference being that the dimension of the matrix of probability and loss is 3×3 for NIST and 5×5 for BS 7799.

Product ranking involves the use of conventional risk values. The level of the related risk reflects the probability of the threat to protected information occurring under the influence of the corresponding vulnerability ( Alfonso, Roldán López de Hierro, & Roldán, 2017).

When using fuzzy-logic tools in the form of an inference mechanism, one can express the presented method for estimating information security risks as the following inference rules.

Input variables:

P i j is the probability of the occurrence of the threat coming from the i th source, which exploits the j th vulnerability;

L O S S i j is the magnitude of loss caused by the occurrence of the threat coming from the i th source, which exploits the j th vulnerability.

Output variable: I N F _ R I S K i j is the magnitude of the information security risk involved in implementing blockchain technology, with that risk coming from the i th source exploiting j th vulnerability.

Logical-inference rules:

(4) I F P i j × L O S S i j ≤ 3 T O I N F _ R I S K i j = l o w

(5) I F 3 < P i j × L O S S i j ≤ 6 T O I N F _ R I S K i j = m i d

(6) I F 8 < P i j × L O S S i j ≤ 12 T O I N F _ R I S K i j = h i g h

(7) I F 15 < P i j × L O S S i j ≤ 20 T O I N F _ R I S K i j = c r i t i c a l

(8) I F P i j × L O S S i j = 25 T O I N F _ R I S K i j = v e r y h i g h

In the inference rules, one can supplement the output conditions or change the number of input variables. Once elaborated, the rules will significantly improve the accuracy of assessing information security risks and the applicability of this method in practice. The final stage of assessing information security risks is making the final report. The management needs that report to make efficient and timely decisions on strategic development, personnel policy, attracting investments, reengineering business processes, and optimizing all types of costs involved in managing corporate resources.

The report must contain accurate and easy-to-understand recommendations for reducing potential loss resulting from the occurrence of all possible information threats that exploit the related vulnerabilities. In essence, the fuzzy-inference mechanism consists in converting input variables to output ones, or a quantification of risk.

At the initial stage, it is necessary to determine input variables for the model. Data for the input variables were obtained with the Delphi method. This called for identifying relationships between the estimated parameters with the logical rule I F … T H E N . The term for each input variable was calculated, and then the value of the membership function for the term was determined. This stage ends once the membership functions for each of the formulated logical rules of fuzzy inference are determined. At the aggregation stage, the logical rules of the fuzzy inference mechanism are formulated for the associated truth degree of the conditions. For that purpose, fuzzy-logic transformations are performed consistent with the logical operations OR, AND, NOT-AND, NOT-OR used to link the conditions in the fuzzy-inference rules at the fuzzification stage. In identifying the results of fuzzy logic, the operations of conjunction (algebraic product) and disjunction (algebraic sum) are used. The aggregation stage is considered completed when the values of truth functions are determined for each of the logical rules. When the model is activated, the truth values for each of the conclusions for the logical rules of fuzzy inference are determined. To complete this stage, it is necessary to establish the weight factors for each logical rule and calculate their algebraic product. The activation stage is considered completed when the associated membership functions are determined for linguistic variables of the logical rules of fuzzy inference.

Purpose of the Study

The principal step in using the premises and mathematical tools of fuzzy-set theory to describe and formulate a model for information security risks is to identify additional object sets – measuring scales and assessment functions. A set of objects that represent measuring scales can be fuzzy, discrete, or continuous. Existing functions for fuzzy assessment of information security risks can be used as a set of assessment functions.

Research Methods

We propose using a generalized formal fuzzy-estimation algorithm to solve the problem of mathematically modeling potential information security risks that come with blockchain technology. The proposed method is based on the mathematical tools of fuzzy-set theory. This made it possible to determine the form of presenting the model for the information security risks of blockchain and formulate an algorithm for assessing information security risks. In essence the method complies with the recommendations of the international standard NIST SP 800-39 for managing information security risks.

Findings

The use of the fuzzy-inference mechanism is based on the use or development of an input-data-processing algorithm. The resulting algorithm must correspond to the study area in that it reflects the relationship between input and output variables or in that it yields various representations for the input data. Given the nuances of providing information security to evaluate information security risks, the Mamdani and Sugeno algorithms can be used. The problem at hand consists in assessing information security risks with fuzzy-logic rules and five-level scales for input variables ( Korablev & Petrushova, 2019).

The surface view of the fuzzy inference in figure 01 shows the dependence of the output variable on several input variables.

See Full Size >

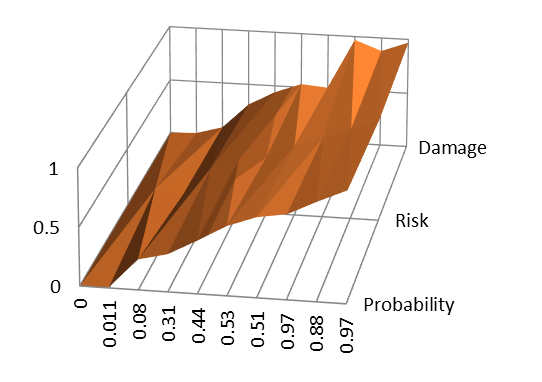
In the figure 01we can see a fairly smooth surface of the plot, which determines the correctness of the inference rules. Fuzzy-inference surfaces can be used to monitor the quality of the fuzzy-inference mechanism. A visual analysis of plots revealed a borderline value of the information risk indicator (0.48), which depends on the potential of the intruder with respect to certain threats.

Conclusion

The fuzzy-inference mechanism is a comprehensive approach to fuzzy modeling since it allows one to factor in the degree of the quality of assessing how effective the security of information resources is (using the associated fuzzy scale); the required level of protection; and the logical-inference rules that determine the variable of the information security risk. Practice shows that the use of toolkits for implementing the fuzzy-inference mechanism makes it possible to simplify information risk management through the use of graphic components. This makes it possible to involve ordinary employees in assessing risks.

References

• Alfonso, G., Roldán López de Hierro, A. F., & Roldán, C. (2017). A fuzzy regression model based on finite fuzzy numbers and its application to real-world financial data. Journal of Computational and Applied Mathematics, 318, 47-58. https://doi.org/10.1016/j.cam.2016.12.001
• British Standards Institute Code of Practice for Information Security Management (BS 7799/ISO 17799) (2019). Retrieved from: http://www.all.net/books/audit/bs7799.html Accessed: 10.07.2019.
• De Gusmão, A. P. H., Silva, L. C., Silva, M. M., Poleto, T., & Costa, A. P. C. S. (2016). Information security risk analysis model using fuzzy decision theory. International Journal of Information Management, 36(1), 25-34. https://doi.org/10.1016/j.ijinfomgt.2015.09.003
• Galbusera, L., & Giannopoulos, G. (2018). On input-output economic models in disaster impact assessment. International Journal of Disaster Risk Reduction, 30, 186-198. https://doi.org/10.1016/j.ijdrr.2018.04.030
• Geras’kin, M. (2018). Modeling reflexion in the non-linear model of the stakelberg three-agent oligopoly for the Russian telecommunication market. Automation and Remote Control, 79(5), 841-859. https://doi.org/10.1134/S0005117918050065 [in Rus.].
• Geras’kin, M., & Chkhartishvili, A. G. (2017). Structural modeling of oligopoly market under the nonlinear functions of demand and agents’ costs. Automation and Remote Control, 78(2), 332-348. https://doi.org/10.1134/S0005117917020114 [in Rus.].
• Groumpos, P. P. (2016). Modelling business and management systems using fuzzy cognitive maps: A critical overview. International Journal of Business and Technology, 4(2), 2. https://doi.org/10.33107/ijbte.2016.4.2.02
• Korablev, A. V., & Petrushova, M. V. (2019). A fuzzy mathematical model for managing the digital transformation of business processes based on cloud services, Espacios, 40(18), 16.
• Korablev, A. V. (2016). The use of cloud technologies in banking. Journal of Economy and Entrepreneurship, 8(73), 463-468. [in Rus.].
• Korablev, A. V., Petrushova, M. V., Pogorelova, E. V., & Abrosimov, A. G. (2019). Mathematical model of economical assessment of investments in information provision for the management system of a modern company. In V. Mantulenko (Ed.), Proceedings of the 17th International Scientific Conference “Problems of Enterprise Development: Theory and Practice” 2018. SHS Web of Conferences, 62 (11002). Les Ulis: EDP Science. https://doi.org//10.1051/shsconf/20196211002
• Luo, J. -L., & Hu, Z. -H. (2016). Risk paradigm and risk evaluation of farmers cooperatives' technology innovation. Economic Modelling, 44, 80-85. https://doi.org/10.1016/j.econmod.2014.10.024
• Masneva, M. F., & Petrushova, M. V. (2016). Internet portals of public services in electronic form. Journal of Economy and Entrepreneurship, 2-1(67), 130-133. [in Rus.].
• National Institute of Standards and Technology Special Publication 800-39 (NIST SP 800-39). Retrieved from: https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-39.pdf Accessed: 13.07.2019.