Complex Evaluation Of Economic Projects Based On Input-Output Tables

Abstract

The article provides an overview of various methods for assessing the effectiveness of investments, provides the concept of a multiplier effect, and also provides an example of the assessment of large economic projects based on the use of intersectoral balance. The question of the criterion of investment efficiency and various approaches to the definition of these criteria are discussed. For private investors, the criterion is maximizing the return on investment for a shorter period of time received directly from the project, and for the state, it can be longer-term goals, such as improving the welfare of the people, etc. Two sample projects have been analyzed in terms of the effectiveness of investments using classical project evaluation methods such as net present value and their comparison with the method of multi-criteria evaluation of projects presented in this paper within the framework of the interindustry balance taking into account interindustry multiplier effects. It is shown that a project that is more effective in terms of direct indicators of return on investment may be less effective from the point of view of the state in comparison with another project that gives less direct return on investment, but has a greater effect on the entire economy, thanks to deeper ties with related industries and manifested multiplicative effects.

Keywords: Evaluation of economic projectsmultiplier effectinter-industry balancepublic investment

Introduction

If we proceed from the fact that the essence of economic science is to search for such solutions and options for the distribution of available resources with which you can get the best economic result, then the study of methods for evaluating economic projects can be considered one of the most practical areas of research.

When evaluating investment projects, as a rule, financial indicators of return on investment are evaluated. The most popular of them are: net present value (NPV), profit investment ratio (PIR), pay-off period (POP), internal rate of return (IRR) ( Schurov & Gotin, 2006; Astarkina, 2012; Denisova, 2014; Blatt, 2019). In domestic and foreign literature, integrated indicators for evaluating the effectiveness of investment projects are often considered ( Koncheva, 2015; Gretchenko, Gorokhova, Demenko, & Gretchenko, 2018; Nadiri, Nandi, & Akoz, 2018; Yermack, 2017; Sychev, Sycheva, & Salnikova, 2018). The integrated indicator is composed of the previously mentioned financial indicators, as a rule, with the addition of weights for each indicator, established by experts.

Such an analysis is useful in evaluating individual economic projects in terms of financial benefits for private investors. When it comes to assessing large economic projects at the federal or regional level, this kind of analysis of financial indicators alone may not be sufficient, especially with the participation of the state as an investor. The decision-making criteria of the state are more blurred. It has many options for investing and a lot of restrictions affecting the choice of areas of economic policy. The ranking of goals is always a problem, since the conflict between short-term and long-term development priorities exists constantly ( Shirov & Yantovsky, 2011).

The interests of private investors are quite obvious - getting as much profit as possible in the shortest possible time and at minimal cost. When an investment project is so large that there are not enough funds from private investors, the state can act as an investor. It, in turn, deciding to invest in any major economic project, calculates how this will affect many factors, ranging from environmental to the preservation of the sovereignty of the country. For example, it can be assumed that in the public sector, the goal is to maximize social welfare. However, this concept is too vague to be used as a working criterion, and therefore it is necessary to use the closest, but specific criteria, such as an increase in national income or a change in the distribution of income as a result of the project.

An additional difficulty in evaluating large investment projects involving the state is the analysis of the complex structure of the relationships in the economy of a country or region, reflected in the multiplier effects of investments in various sectors of the economy. This requires the use of deeper methods to analyze the impact of projects on the entire economy.

Problem Statement

Public state investments have an important criterion for evaluating the effectiveness of the investment, which is the calculation of the multiplier effects. The essence of the multiplier effect is that with an increase in any of the components of autonomous expenses, it leads to an increase in the national income of the country, and by an amount greater than the initial costs.

This term was first introduced by Keynes ( 1936). It was demonstrated that government spending on organizing public works not only leads to job creation, but also stimulates an increase in consumer demand, thereby contributing to the growth of production and employment in the economy as a whole. Later, in addition to the employment multiplier, income and investment multipliers were allocated.

The tasks of assessing the impact of gross output and capital investment within one industry on the entire national economy as a whole arise quite often, especially when choosing priority areas for state support of large investment projects ( Clopper, 2018). The method of calculating the multiplier that is most often found in the literature is based on a comparison of statistical data on how much the value of the economic indicator under study varies depending on the dynamics of another economic indicator ( Cooper, Owen, Cooper, & Serrenho, 2015).

However, sectors of the economy have different weights in total gross output (i.e., economic structures are included with varying degrees of depth) ( Akhmadeev & Moiseev, 2017), thus, at constant rates of change in production dynamics, nominal output increases in various forms activities will vary significantly. This means that an activity having a high multiplier coefficient, but at the same time having a relatively lower weight in the economy, should have a less multiplier effect compared to a more significant industry.

Research Questions

We distinguish two different types of multiplicative effect: the first - due to own multiplicative effects of production, the second - due to multiplicative effects from interindustry interactions. For example, the automotive industry has a significant number of intersectoral relations with other sectors of the economy: metal mining, petrochemicals, instrumentation, etc., as well as the production of which involves a large number of qualified specialists, thus the multiplier of employment through other involved industries is manifested.

In the domestic scientific literature there is a considerable number of examples of the study of interbranch multiplicative effects through the study of interbranch balance ( Shirov & Yantovsky, 2011; Tatarkin, Sidorova, & Trynov, 2015). In the above articles, as a rule, the effect of multipliers on gross output when changing production volumes of an individual industry is studied. However, the authors of this article are interested in evaluating two or more potential projects for implementation, moreover, when the investor is the state.

Purpose of the Study

As the purpose of this research we consider the application of intersectoral balance to the assessment of large-scale economic projects, initiated by the government. As the result we want to show, that traditional methods of project evaluation do not incorporate the multiplicative effects, arising from interconnections with other industries, and thus cannot comprise the overall economic effect of such project. Proposed method can be successfully adopted for comparing economic effect of a set of alternative projects, given arbitrary target criterion.

Research Methods

As you know, the gross output of industries and the vector of final consumption are related by the dependence of the form:

$$\begin{array}{}\text{(1)}& X_{\mathrm{0}}={\left(I-A_{\mathrm{0}}\right)}^{-\mathrm{1}}Y\end{array}$$ ,

where I is the identity matrix, and $A_{\mathrm{0}}$ is the production matrix.

Suppose that there are two alternative projects, of which only one can be accepted due to budgetary constraints. Then, the gross output vector when adopting the first draft will be expressed as follows:

$$\begin{array}{}\text{(2)}& X_{\mathrm{1}}={\left(I-A_{\mathrm{1}}\right)}^{-\mathrm{1}}{Y}_{\mathrm{1}}\end{array}$$ ,

and when accepting the second draft, this is expressed as:

$$\begin{array}{}\text{(3)}& X_{\mathrm{2}}={\left(I-A_{\mathrm{2}}\right)}^{-\mathrm{1}}{Y}_{\mathrm{2}}\end{array}$$ ,

where $A_{\mathrm{1}}$ is the production matrix with the implementation of the 1st project, and $A_{\mathrm{2}}$ is the 2nd project. In this article we will use an unchanged vector of final consumption: Y = $Y_{\mathrm{1}}$ = $Y_{\mathrm{2}}$

Denote the share of value added by products of each industry as w_i∈ [0,1]. Then the following equality holds:

$$\begin{array}{}\text{(4)}& x_i=w_i\times x_i+(\mathrm{1}-w_i)\times x_i\end{array}$$ ,

where $x_i$ is the gross output of the i-th industry.

Further, suppose that the added value of the products of each industry is divided in a certain proportion between profit and taxes. Then tax revenues from the i-th industry can be written as follows:

$$\begin{array}{}\text{(5)}& t_i=z_i\times w_i\times x_i\end{array}$$ ,

Where $z_i$∈ [0,1] is the share of tax revenues of the i-industry.

The total tax revenue from the functioning of all sectors can be presented in matrix form, as shown below:

$$\begin{array}{}\text{(6)}& \underset{i=\mathrm{1}}{\overset{N}{\sum }}{t}_i={\left(Z°W\right)}^T\times X\end{array}$$

Thus, the indicator of financial return from the implementation of each of the projects without taking into account initial investments (they are assumed to be equal in this work) can be presented in the following form, respectively, for the first ( 6 ) and second project ( 7 ):

$$\begin{array}{}\text{(7)}& P{V}_{\mathrm{1}}={\left(Z_{\mathrm{1}}°W_{\mathrm{1}}\right)}^T\times X_{\mathrm{1}}+(\mathrm{1}-z_{new\mathrm{1}}){\times w}_{new\mathrm{1}}\times x_{new\mathrm{1}}\end{array}$$

$$\begin{array}{}\text{(8)}& P{V}_{\mathrm{2}}={\left(Z_{\mathrm{2}}°W_{\mathrm{2}}\right)}^T\times X_{\mathrm{2}}+(\mathrm{1}-z_{new\mathrm{2}})\times w_{new\mathrm{2}}\times x_{new\mathrm{2}}\end{array}$$

where the first term is responsible for the multiplier effect from the implementation of the corresponding project, and the second for profit, directly from the project (here it is assumed that the state in this case is the sole shareholder).

It should be noted that according to the classical system for evaluating the effectiveness of a project, the indicator of financial return from the implementation of projects is written in the following form, respectively, for the first ( 8 ) and second project ( 9 ):

$$\begin{array}{}\text{(9)}& \widehat{P{V}_{\mathrm{1}}}=w_{new\mathrm{1}}\times x_{new\mathrm{1}}\end{array}$$

$$\begin{array}{}\text{(10)}& \widehat{P{V}_{\mathrm{2}}}=w_{new\mathrm{2}}\times x_{new\mathrm{2}}\end{array}$$

Given the assumed equality of investment costs, the project is adopted whose financial return is higher.

$$\begin{array}{}\text{(11)}& \widehat{P{V}_{\mathrm{1}}}>\widehat{P{V}_{\mathrm{2}}}\end{array}$$

Findings

The statistical base for the implementation of numerical experiments on real data was the basic table of input-output by the Russian Federal State Statistics Service. This database consists of 3 quadrants (sections), where the first quadrant is the symmetric square matrix for 126 industries, where the output is expressed in rows, and the costs of each of the industries are displayed in columns, the second quadrant is the final output of the industries, distributed for home production farms, export, stockpiling, etc. The third quadrant shows the volume and distribution of gross value added by industries for labor remuneration, tax deductions, industry profits, etc.

In our experiment, we consider two alternative projects that produce products only for final consumption, which replaces industry products No. 1. First, suppose that the first and second projects are completely identical and have the same cost structure. After that, we will gradually redistribute the costs for the second project in the first scenario from 4 industries to 6 and in the second - from 4 industries to 5. In fact, it turns out that from the point of view of the classical approach to assessing project effectiveness, the two considered are equivalent, since the total costs do not change, but only their structure changes. Nevertheless, from the point of view of an integrated approach to assessing the aggregate effect of introducing a new project, the aggregate effect of tax revenues can be estimated according to the above formulas. Figure 01 shows the dynamics of changes in the cumulative effect of the adoption of the second project instead of the first, with a gradual redistribution of funds from one industry to another.

See Full Size >

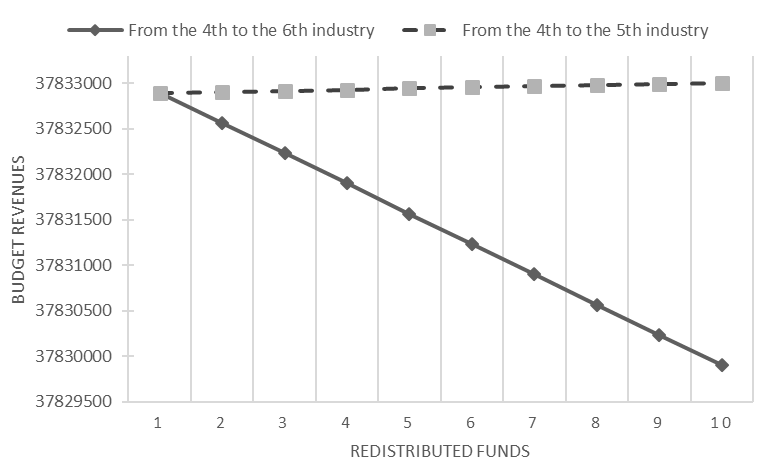
Conclusion

We can conclude that as a result of the implementation of the classical approach to assessing the effectiveness of state projects, the cumulative economic effect of their introduction is not taken into account, which may lead to the choice of a less efficient project. The article proposes a method that reflects the cumulative economic effect of the introduction of a project, since it takes into account its interaction with other sectors of the economy, which allows a more reasonable and reliable assessment of its effectiveness.

References

• Akhmadeev, B. A., & Moiseev, N. A. (2017). The method of calculation of the coefficient of influence of the industry on the economy. Audit and financial analysis, 1, 69-73. [in Rus.].
• Astarkina, N. R. (2012). An integrated methodology for evaluating the effectiveness and choice of an investment project in small businesses. Economic sciences, (7)92,131-134. [in Rus.].
• Blatt, J. M. (2019). Dynamic economic systems: A post Keynesian approach. New York, NY: Routledge.
• Clopper, A. (2018). Why are input-output tables important? Studies on Russian Economic Development, 29(6), 584-587. https://doi.org/10.1134/S1075700718060060
• Cooper, S., Owen, A., Cooper, S., & Serrenho, C. (2015). Disaggregated monetary input-output tables as an alternative to physical input-output tables. In Max Lu G.Q. (Ed.), Proceedings of ISIE Conference 2015 - Taking Stock of Industrial Ecology, 7. New Haven, Connecticut, USA: International Society for Industrial Ecology.
• Denisova, T. V. (2014). Method of the reliability analysis of investment projects optimization variants. Izvestia of Samara Scientific Center of the Russian Academy of Sciences, 16(6(2)), 430-433. [in Rus.].
• Gretchenko, A. I., Gorokhova, I. V., Demenko, O. G., & Gretchenko, A. A. (2018). Digital Economy: Challenges and Threats for Modern Russia. Journal of Advanced Research in Law and Economics, 9(4), 1243-1248. https://doi.org/10.14505//jarle.v9.4(34).09
• Keynes, J. M. (1936). The general theory of employment, interest and money. London: Macmillan.
• Koncheva, E. O. (2015). Assessment of Transportation Projects Impact on Regional Development: Applicability of International Experience in Russian Federation. Public Administration. Electronic Bulletin, 52, 163-176. [in Rus.].
• Nadiri, M. I., Nandi, B., & Akoz, K. K. (2018). Impact of modern communication infrastructure on productivity, production structure and factor demands of US industries: Impact revisited. Telecommunications Policy, 42(6), 433-451. https://doi.org/10.1016/j.telpol.2018.03.008
• Schurov, B. V., & Gotin, A. E. (2006). Analysis of the method of selection of investment projects based on the methods of multipurpose optimization. Economic Analysis: Theory and Practice, 8(65), 2-7. [in Rus.].
• Shirov, A. A., & Yantovsky, A. A. (2011). Evaluation of the multiplier effects in the economy: opportunities and limitations. ECO, 2(440), 40-58. [in Rus.].
• Sychev, V., Sycheva, G. A., & Salnikova, Y. (2018). The value analysis in the investment evaluation of innovative productions. In J. Kantola, T. Barath, & S. Nazir (Eds.), Proceedings of the AHFE 2017 International Conferences on Human Factors in Management and Leadership, and Business Management and Society. Advances in Human Factors. Business Management and Leadership, 594 (pp. 20-27). Cham: Springer. https://doi.org/10.1007/978-3-319-60372-8_3
• Tatarkin, D. A., Sidorova, E. N., & Trynov, A. V. (2015). Methodical bases of estimation multiplicative effect of the realization of socially significant investment projects. Bulletin of Ural Federal University. Series Economics and Management, 14(4), 574-587. https://doi.org/10.15826/vestnik.2015.14.4.033
• Yermack, D. (2017). Corporate governance and Blockchains. Review of Finance, 21(1), 7-31. https://doi.org/10.1093/rof/rfw074