Queueing System In The Optimization Of The Labor Process Of Pharmaceutical Employees

Abstract

Implementation of the queueing system for solving the tasks of management of pharmaceutical goods flow was investigated on the example of the pharmacy of the multipurpose medical organization. Optimization of the labor process of pharmaceutical employees in the pharmacy is an urgent scientific problem of the pharmaceutical activity sphere aimed at improving the quality of drug provision for patients. In the course of the research the methods of documentary observation and stopwatch measurement of standard operating procedures of processing the requisition notes for medicinal products and medical items by pharmaceutical workers with the help of personal computers and special software were used. The pharmacy, which is a structural unit of the multipurpose clinical medical organization with a bed capacity of 620 beds was chosen as the experimental base. The studied queueing system is represented by n - queueing channels and the unlimited queue. The main criterion for optimizing the work of the pharmacy is the requisition note processing time spent by the structural unit of the medical organization on keeping the application in the queue. Variable indicators are the average number of requisition notes per month, the number of items of pharmaceutical goods in one requisition note and the number of simultaneously occupied channels of their processing. The average time of requisition note processing in the system is 17 minutes. It is established that pharmaceutical employees spend up to 80% of their time on operational work, which meets the requirements of labor legislation and allows them to maintain stable performance.

Keywords: Pharmaceutical employeesqueueing system

Introduction

Queuing System (QS) is one of the sections of probability theory that is currently widely used for optimization of labor processes (Boyarinova, Ismailov, & Potapova, 2015; Lakhmi & Sivakumar, 2013; Bissell, Traulsen, & Haugbølle, 2002). It is especially important to properly organize the labor process of pharmaceutical employees in the pharmacy of the multipurpose medical organization (MO) that performs production, supply, information and other functions.

Problem Statement

The study was carried out in order to solve the scientific problem of optimizing the labor process of pharmaceutical employees of the pharmacy of the multipurpose MO.

Research Questions

The results were aimed at solving an important practical issue, namely the analysis of the efficiency of working time usage by the pharmacy staff of the multipurpose MO (Bader, McGrath, Rouse, & Anderson, 2017).

Purpose of the Study

Scientific substantiation of the mathematical model of the QS for the timely processing of the requisition notes (applications) for dispensation of medicinal products (MP) and medical items (MI) from the pharmacy to the medical units of the multipurpose MO.

Research Methods

In the course of the research the methods of documentary observation and stopwatch measurement of standard operating procedures of processing the requisition notes for MP and MI by pharmaceutical workers with the help of personal computers and special software were used.

Findings

The study was carried out on the basis of the pharmacy, which is a structural unit of the multipurpose clinical medical organization with a bed capacity of 620 beds. It is established that up to 15 thousand patients are treated in the MO annually. Normal bed capacity is distributed as follows: surgical beds – 49.9%; therapeutic – 41.8%; infectious – 8.3%. The MO has 36 departments, a blood transfusion station, an experimental laboratory, a Pathology Department and other units at its disposal. The MO has licenses for pharmaceutical activities with the right to manufacture MP according to individual prescriptions and requirements of the MO units, as well as for activities related to the circulation of narcotics and psychotropic substances.

The pharmacy of the MO is located in a separate building and is connected to the main and other medical buildings by underground passages, which allows to carry out transport logistics of pharmaceutical products in the MO units regardless of weather and climatic conditions. The total area of functional premises of the pharmacy is 812 m2. The premises of the pharmacy are fitted with all necessary equipment.

The pharmacy's staff includes 22 employees. At the time of the research staffing was 100%. Analysis of the pharmacy personnel of the MO (Figure 01 ) showed that the share of administrative and managerial staff accounts for 18.2%, production personnel – 59.1%. The pharmacy employs 9 senior pharmacists (40.90%) and 8 pharmacists (36.36%), the share of pharmacy technicians (packers – 3 people and nurse's aides – 2 people) accounts for 22.72%. It should be noted that the majority of specialists have higher and secondary professional (pharmaceutical) education and more than 10 years of experience. Among the staff of the pharmacy, 66.7% of senior pharmacists and 87.5% of pharmacists have the highest qualification categories.

See Full Size >

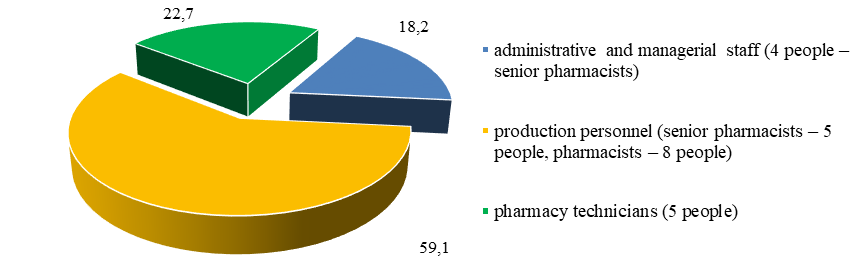
Employment position instructions are compiled for each worker of the pharmacy of the MO, providing for the rights, duties, interchangeability by position in the current daily work and in conditions of additional workload (Kabakova, Davidov, & Goryachev, 2011). Training seminars are regularly held to improve and deepen the knowledge of pharmaceutical employees in the field of drug provision for the population.

During the working shift, senior pharmacists perform their labor functions, working on personal computers, so it was regarded as appropriate to further consider the work of the pharmacy organization as a mathematical model of the QS with multiple channels and the unlimited queue.

Despite the fact that the pharmacy is a structural unit of the MO, the processing of requisition notes for MP and MI can be considered as a closed system, since they arrive at the pharmacy from the medical departments at the end of each working day (Kirpichnikov, 2011). During the research, we took into account the fact that the number of requisition notes for MP and MI on a certain day depends not only on the number of patients being currently treated at the in-patient department of the hospital, but also on the structure and severity of their diseases.

Most QS consider various parameters, among which the number of channels, the length of the queue and the waiting time are the most important. Moreover, the queueing system with multiple channels, the presence of the queue with limited waiting time is the most common one (Shapochnikov, Berezhnoj, Lyagin, & Pletuhina, 2017; Shemahin, 2015; Sahu, A., Sahu, N., Sahu, B., & Sahu, A., 2013).

Analysis of standard operating procedures performed by pharmaceutical workers showed that a significant part of them is done on personal computers, and the request for service is made in the form of a requisition note of a particular medical department of the MO. For the sake of objectivity, it was assumed that the flow of requisition notes for MP and MI is random, and can be regarded in terms of the Poisson distribution (Nickman, Guerrero, & Bair, 1990; Gregório, Russo, & Lapão, 2016).

To determine the input parameters of the model the necessary statistical observations were made during the first half of the year 2018. The number of requisition notes (applications) received daily at the pharmacy ranged from 90 to 124, so the frequency of incoming requisition notes is an important factor for determining the workload of the employees. Summarizing the statistical observations, we built a histogram of the relative frequencies of the average number of requisition notes received by the pharmacy per month (Figure 02 ).

See Full Size >

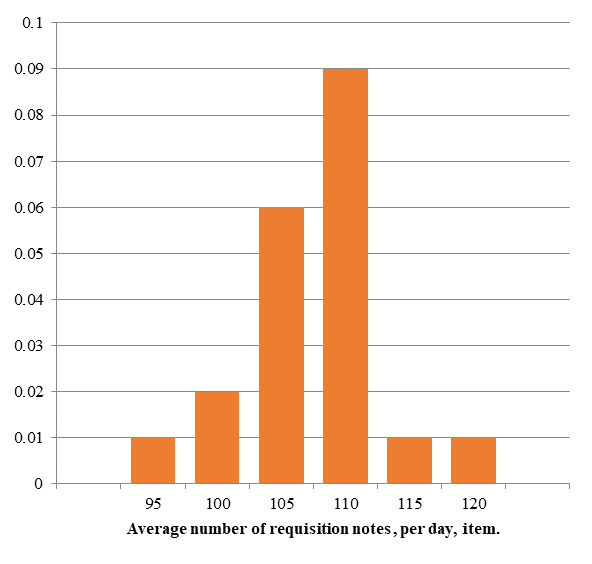
It is revealed that the number of names of MP and MI in each requisition note (application) is a random value, which varied from 1 item to 30. Thus, by direct observation and stopwatch measurement, it is established that requisition note processing time varied from 4 to 40 minutes. Statistical data of observations are presented on the histogram of relative frequencies of the average time of one requisition note (application) to be processed (Figure 03 ).

See Full Size >

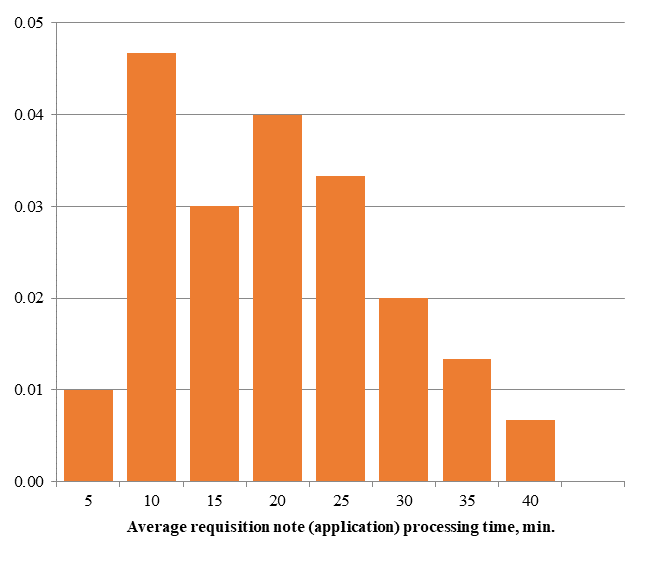
Since the processing of requisition notes for MP and MI is carried out using a personal computer, the established average rate of processing time of one item per name of MP in the requisition note with several names was 1-2 minutes.

It should be noted that the queueing system has multiple channels. All queueing channels offer the same services, that is, there is a parallel service with simultaneous processing of requisition notes received from several medical departments. The mathematical model of the Queuing System with n-channels and an unlimited queue is presented as a graph (Figure 04 ), where: – the flow intensity of requisition notes, – the flow intensity of processing, n – the number of queueing channels.

See Full Size >

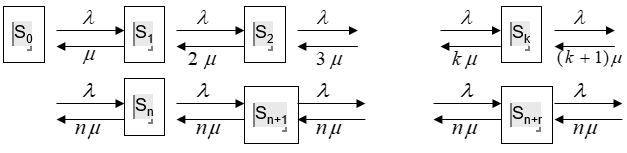
In the proposed mathematical graph, it is implied that: S0 – all channels are free; Sn – all channels are occupied, the queue is empty; Sn+r – all channels are occupied, r requisition notes are in the queue.

Further, the designation of the flow intensity of requisition notes was introduced. $\rho =\frac{\lambda }{\mu }$ . It should be noted that at $\frac{\rho }{n}<\mathrm{1}$ the limiting probability exists, but at $\frac{\rho }{n}\ge \mathrm{1}$ the length of the queue grows to infinity.

The limiting probabilities of a system in the “steady state” are as follows:

$p_{\mathrm{0}}={\left(\mathrm{1}+\frac{\rho }{\mathrm{1}!}+\frac{{\rho }^{\mathrm{2}}}{\mathrm{2}!}+\dots +\frac{{\rho }^n}{n!}+\frac{{\rho }^{n+\mathrm{1}}}{n!(n-\rho )}\right)}^{-\mathrm{1}}$,

$p_{\mathrm{1}}=\rho p_{\mathrm{0}};p_{\mathrm{2}}=\frac{{\rho }^{\mathrm{2}}}{\mathrm{2}!}{p}_{\mathrm{0}};p_k=\frac{{\rho }^k}{k!}{p}_{\mathrm{0}},\dots ,p_{n+r}=\frac{{\rho }^{n+r}}{n^r\cdot n!}{p}_{\mathrm{0}}$ The probability that the requisition note (application) will be in the queue: $P_{o\mathrm{4}}=\frac{{\rho }^{n+\mathrm{1}}}{n!(n-\rho )}\times p_{\mathrm{0}}$. The average number of channels occupied with processing (The average number of occupied channels): $\stackrel{-}{k}=\frac{\lambda }{\mathrm{\mu }}=\rho$.

The average number of requisition notes (applications) in the queue: $L_{ou}=\frac{{\rho }^{n+\mathrm{1}}}{n\cdot n!{\left(n-\frac{\rho }{n}\right)}^{\mathrm{2}}}\times p_{\mathrm{0}}$ .

The average number of requisition notes (applications) in the system: Lсист = Lоч + ρ.

The average time spent in the system: $T_{cucm}=\frac{\mathrm{1}}{\lambda }{L}_{cucm}$ .

The average time spent in the queue: $T_{o\mathrm{4}}=\frac{\mathrm{1}}{\lambda }{L}_{ou}$ .

At $\frac{\rho }{n}<\mathrm{1}$ for QS with an unlimited queue, any requisition note (application) will be processed, that is, the probability of failure Pотк = 0, relative flow capacity Q = 1, absolute flow capacity A = .

Thus, there are 5 channels with the unlimited queue and flow intensity of 108 requisition notes (applications) per day (eight-hour working day) in the pharmacy of the multipurpose MO. The average requisition notes processing time in the system tср = 17 minutes.

Later on, the performance indicators of the system were detected. The processing intensity $\mu =\frac{\mathrm{60}}{\mathrm{17}}\approx \mathrm{3.529}$ of requisition notes (applications) per hour, reduced processing flow intensity $\rho =\frac{\lambda }{\mu }=\frac{\mathrm{14}}{\mathrm{3.529}}\approx \mathrm{3.967}$. As $\frac{\rho }{n}=\frac{\mathrm{3.967}}{\mathrm{5}}<\mathrm{1}$ , the length of the queue will not grow indefinitely.

Probability that the channel is free (share of idle time of channels): p0 = 0.0137. So, 1.37% of time during one hour the channel will not be occupied, that is the idle time is tпр = 0.8 minutes.

Probability that the processing is performed by: 1 channel p1 = 0.054; 2 channels: p2 = 0.108; 3 channels: p3 = 0.142; 4 channels: p = 0.141; 5 channels: p5 = 0.112.

Probability that the requisition note (application) will be in the queue: Роч = 0.429.

The average number of requisition notes (applications) in the queue, item.: Lоч = 2,078.

The average number of requisition notes (applications) in the system, item: Lсист = 6.045.

The average time spent in the system, hour: Тсист = 0.432.

The average time spent in the queue, hour: Точ = 0.14.

The average number of channels occupied with processing (The average number of occupied channels), item: $\stackrel{-}{k}$ = 3.967.

The average number of idle channels: 1

It should be emphasized that the necessary condition of the QS operability is observed in the studied pharmacy of the MO (Svetlov, 2007):

$\stackrel{-}{k}$ < n,

where: $\stackrel{-}{k}$ – the average number of occupied channels; n – the number of channels.

Channel occupancy rate is equal to $K_{\mathrm{3}}=\frac{\stackrel{-}{k}}{n}=\mathrm{0.8}$ , consequently, the system is 80% busy with processing. This indicator also shows that pharmaceutical employees spend 80% of their working time on processing requisition notes (applications) using personal computers, which is an appropriate indicator for the organization of the labor process allowing their sustainable performance to be maintained.

Conclusion

The parameters of requisition notes (applications) processing by the pharmacy aimed at providing MP and MI for the medical units of the MO, investigated using a mathematical model of the QS, show that pharmaceutical employees fully realize their work potential, make an efficient use of their working time. The pharmacy of the MO successfully performs logistics procedures and gets a useful effect of the rational use of working time.

References

1. Bader, L. R., McGrath, S., Rouse, M. J., & Anderson, C. (2017). A conceptual framework toward identifying and analyzing challenges to the advancement of pharmacy. Research in Social and Administrative Pharmacy, 13(2), 321-331.
2. Bissell, P., Traulsen, J. M., & Haugbølle, L. S. (2002). Sociological Theory and Pharmacy Practice Research: The contribution of interactionist sociology to understanding the experience of health and illness. International Journal of Pharmacy Practice, 10(3), 213-224.
3. Boyarinova, I. N., Ismailov, T. R., Potapova, I. A. (2015). Modelirovanie i optimizaciya raboty sistemy massovogo obsluzhivaniya [Simulation and optimization of the queuing system]. Fundamental'nye issledovaniya [Fundamental Research], 9, 9–13. [in Russ.].
4. Gregório, J., Russo, G., & Lapão, L. V. (2016). Pharmaceutical services cost analysis using time-driven activity-based costing: A contribution to improve community pharmacies’ management. Research in Social and Administrative Pharmacy, 12(3), 475–485.
5. Kabakova, T. I., Davidov, S. B., & Goryachev, A. B. (2011). Farmacevticheskaya pomoshch' postradavshim v chrezvychajnyh situaciyah, na primere krupnogo mnogoprofil'nogo lechebnogo uchrezhdeniya [Pharmaceutical assistance to victims in emergency situations, on the example of a large multipurpose medical institution]. Sostoyanie i perspektivy razvitiya sluzhby mediciny katastrof. [“State and Development Prospects of Emergency Medicine”], All-Army Scientific and Practical Conference, pp. 104–105. Moscow. [in Russ.].
6. Kirpichnikov, A. P. (2011). Methods of applied queuing theory. Kazan': Kazanskij Gosudarstvennyj universitet. [in Russ.].
7. Lakhmi, C., & Sivakumar, A. I. (2013). Application of queuing theory in health care: A literature review. Operations Research for Health Care, (1–2), 25-39.
8. Nickman, N. A., Guerrero R. M., & Bair, J. N. (1990). Self-reported work-sampling methods for evaluating pharmaceutical services. American Journal of Hospital Pharmacy, 47(7), 1611–1617.
9. Sahu, A. K., Sahu, N. K., Sahu, B., & Sahu, A. K. (2013). Determining Flow of Arrivals in Decision Making by the Application of Queuing Theory. International Journal of Science and Research, 6(14), 306-309. Retrieved from https://www.ijsr.net/conf/NCKITE2015/136.pdf
10. Shapochnikov, A. V., Berezhnoj, V. V., Lyagin, A. M., & Pletuhina, A. A. (2017). Queuing System Theory. Stavropol', Russion Federation: “SKFU”. [in Russ.].
11. Shemahin, E. Yu. (2015). Simulation of an open type queuing system. European Research, 2(3), 5-9. [in Russ.].
12. Svetlov, N. M. (2007). Queuing systems. Retrieved from https://studylib.ru/doc/4881219/sistemy-massovogo-obsluzhivaniya. [in Russ.].