Abstract
This paper deals with some issues related to the training of students of junior courses (approximately 14–19 years). At least two objectives are set. Firstly, we focus on potential participants of the programming Olympiads: according to our calculations, at least one third of the tasks of high-level competitions can be called exhaustive- searched. Secondly (which, apparently, is more important), mastering the proposed approach to the implementation of hard exhaustive-searched problems can (and should) serve as an “advanced” student as a first step into the “big science”: the tasks themselves, and the approach we propose to implement them, are closely connected with the set of directions of modern artificial intelligence, the analysis of large data, and similar subject areas. Several of the problems we are considering are related to different subjects. Among these problems (subjects areas) are, first, the tasks previously given at different levels of the ACM Olympiads, including at the final stage of this competition. The solutions we offer for these tasks are no more complicated than the original ones, and considering that they can be quickly implemented using the approach we proposed (described in this article), we can say that they are much easier to learn by the trainees. In the paper, we describe some classes implemented in C++, intended for the quick generation of programs for solving a variety of enumeration problems. We give also some specific programming techniques for such problems.
Keywords: Complex enumeration problemsan approach to the implementationоlympiads problemsthe first step in the science
Introduction
This paper deals with some issues related to the training of students of junior courses (approximately 14–19 years). These questions are related to the approach to the implementation of programming algorithms for solving brute-force problems. In the opinion of the authors of the paper, the proposed approach can even be considered as a possible standard designed to develop and design algorithms for solving exhaustive problems. To note that, of course, the paper deals with the generalization of “advanced” high school students and junior students. At the same time, the following objectives are set.
Problem Statement
Firstly, we focus on potential participants of the programming Olympiads. We present an easily realizable method for solving an entire class of enumeration problems. It can be called an approach to the implementation of a set of algorithms based on the method of branches and bounds, which includes many additional similar heuristics; this uniformity lies in the fact that the heuristics themselves do not practically change when passing from one task to another.
Therefore, according to (Cormen, Leiserson, Rivest, & Stein, 2009; Lipski, 2004) etc., we called this method a multi-heuristic approach. The complexity of the tasks we solve using this approach is very different: from “student Olympiad” problems to large software projects, often representing a complex of heuristic algorithms for the practical solution of some NP-difficult problem. It should be noted that despite this, the setting and implementation of our proposed tasks is available to a 16–17 year old “advanced” student.
In our previous publications, almost nothing was said on the implementation of algorithms; and in this paper, we try to eliminate this defect. According to the authors, in many scientific publications devoted to the descriptions of algorithms, as well as in various textbooks, the actual implementation of programs is often “overlapping taboo”. Moreover, there is often a much worse situation, the next one. The very texts of the programs, given in very good books (like (Java Platform, 29 May 2018; The 2007 ACM Programming Contest World Finals, 29 May 2018)), seem somewhat “unfinished”, simply because the authors practically do not pay attention to “purely programming” questions. Among these issues, we first of all note the allocation and release of dynamic memory, etc., but not only them. And for the implementation of the programs described by us, it seems that quite enough knowledge of a small subset of C++; it should be a small one, but a “good” subset, a self-succient one.
Secondly (which, apparently, is more important), mastering the proposed approach to the implementation of hard exhaustive-searched problems can (and should) serve as an “advanced” student as a first step into the “big science”: the tasks themselves, and the approach we propose to implement them, are closely connected with the set of directions of modern artificial intelligence, the analysis of large data, and similar subject areas.
Several of the problems we are considering are related to different subjects. Among these problems (subjects areas) are, first, the mentioned before tasks previously given at different levels of the ACM Olympiads, including at its final stage. The solutions we offer for these tasks are no more complicated than the original ones, and considering that they can be quickly implemented using the approach we proposed (described in this article), we can say that they are much easier to learn by the trainees. The second class of subject areas is various classical hard-to-solve brute-force problems, usually NP-difficult; as examples, we assume to result in the continuation article a very similar program applied to much more complex problems: the traveling salesman problem in the classical formulation, the problems of computing certain invariants of a graph, and the problem of state minimization for nondeterministic finite automata. We shall set one more goal to consider a concrete example of one of such problems. This analysis will include the basics of the necessary mathematical theory. In the current paper, we describe some classes implemented in C++, intended for the quick generation of programs for solving a variety of enumeration tasks. Examples of programs that are accessible for understanding by an “advanced” junior student of 14–15 years who owns the very basics of object-oriented programming are given. The following different things should be noted (sometimes once again):
perhaps in our case, the implementation does not provide the fastest solution, but it provides a method for solving several Olympiad problems of different levels;
some programming subtleties are explained in the comments to the programs; this is why we present the texts of the programs in more or less detail;
our approach to such implementation constitutes an essential part of the subject of this paper; greatly simplifying the situation, it is the first step on the way to science;
the MFC class library used by us (and perhaps a little “outdated”) has exact analogues for a “much more modern” API interface library (its description is given, e.g., in (Russel & Norvig, 2010).
Research Questions
Let us start with one of the problems of the 2007 ACM finals, namely, from task F (Luger, 2008) etc. This is the problem of the finals of the most prestigious international student’s world championship (even one of the simplest tasks offered there), but its level is approximately such that when solving “off-line”, its complexity is quite accessible to the “advanced” high school student. As already noted above, when we consider it, we actually get a method for solving similar search problems.
So, we give the condition of the problem and we will note in advance that we have slightly simplified the formulation of the condition when deciding. For example, we will consider only the case N = 4. Besides, we did not replace the word “blue” in the wording: even in the case of a black-and-white picture, the meaning is obvious.
Purpose of the Study
The end of the game is when each ball falls into the hole with the corresponding number (Figure
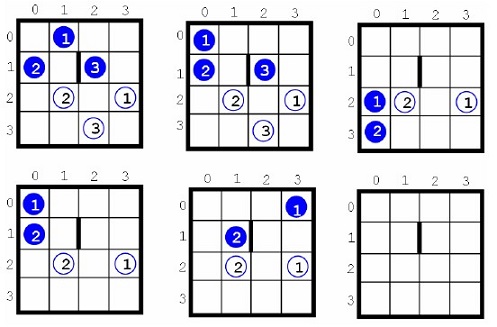
Figure
Before discussing the solution, it should be noted that instead of the term “game” it is more accurate to use the word “puzzle”, which is more in line with the terminology used in the literature on artificial intelligence (Hromkoviˇc, 2011; Melnikov & Pivneva, 2016). However, when considering the condition of the problem, we left the terminology of the original. And since this is a puzzle, then we can apply the usual method of solving them, i.e. a complete search in the state space. But, as it was mentioned in the introduction, our approach to solving similar problems, to organizing the search in them (more precisely, the search with returns, backtracking) can be applied to other, much more complex problems. In Figure
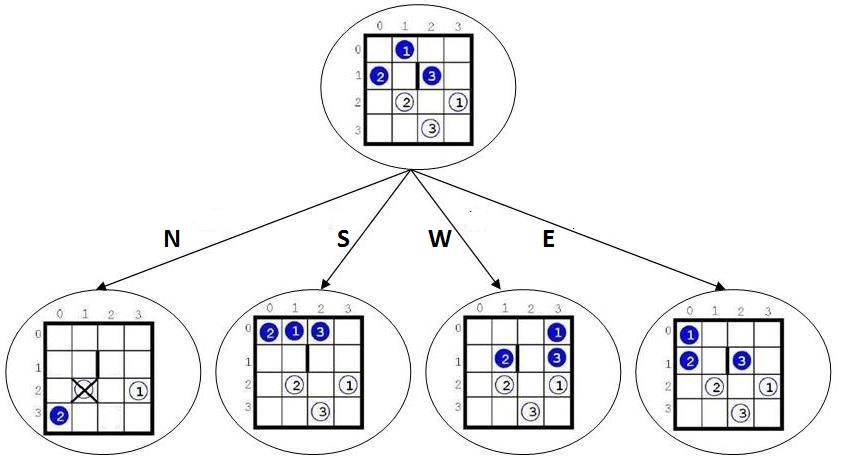
So, the full search (the brute force method) is considered. At the same time, we must:
firstly, prevent possible loops (in the search tree, i.e. in this case, in the tree of positions);
secondly, find the optimal solution (minimum in the number of moves);
and thirdly, be able to find situations in which there is no solution.
All this leads to the idea of using a search in breadth – which we will do.
We will not save the entire search tree. Here – and more importantly, that everywhere in such situations – it is enough (and desirable!) to store only the leaves of this tree; and since we decided to organize a search in width, then it is desirable to store the leaves in the form of a queue, see (Melnikov, 2017; Melnikov, 2018) etc. (And in the case of searching the most convenient version of the data in depth, it appears that the stack is also conveniently organized on the basis of an array or list.) We implement the queue using the simplest array (pointers to the vertices-positions). In the next program, each such vertex will be of type MyBoard. And we will be the easiest way to prevent possible looping: we will remember all the positions that we met.1 So, in our program there will be even 2 arrays: in one we will store the positions not yet considered, and in the other is already considered. At the beginning of the work, the first one (the main one) consists of a single element (corresponding to the starting position), the second one is generally empty. Next, we sequentially delete the first element of the main array, the current position (adding it simultaneously to the second array), and write instead three positions to it, at the end of the main array (the main queue!), each of which can be obtained from the current one in 1 move.2 The values of the main array (list) after the first and second iterations are shown in Figures
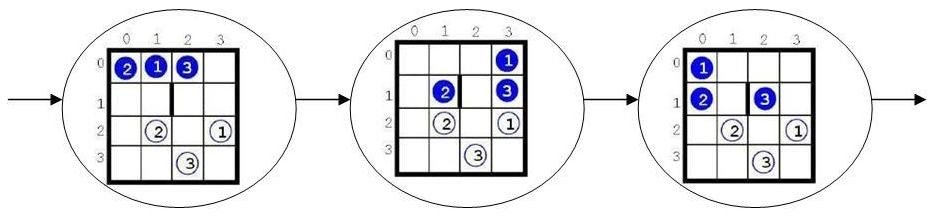
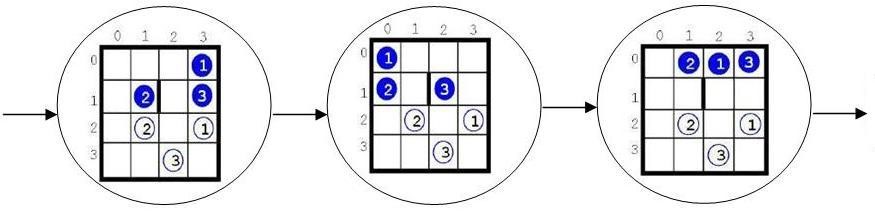
Research Methods
Let us turn to the description of the software implementation. We use objectoriented programming and the simplest classes of library MFC (Pivneva, Melnikov, & Kuptsov, 2016; Melnikov, 2018). It is important to note that it is this implementation that constitutes an essential part of the subject of this article. Also, let us note once again, that the MFC class library used by us (and perhaps a little “outdated”) has exact analogues for a “much more modern” API interface library.
So, the following description of the class-position (MyBoard) is possible:
class MyBoard {
private:
int nDim; // dimension
int Board [4][4];
bool WallRight [4][3]; // the wall is to the right of this cell
bool WallDown [3][4]; // the wall is from below of this cell
int nDeep;
// level, depth of search (the number of moves already made)
int nLast;
// the last made move:
// 0 - we do not know; 1 - nord; etc.
public:
MyBoard ();
MyBoard (MyBoard& copy); // copy constructor
int GetDim () { return nDim; }
int Get (int i, int j) { return Board[i][j]; }
int GetDeep () { return nDeep; }
int GetLast () { return nLast; }
friend istream& operator>> (istream& is, MyBoard& board);
friend ostream& operator<< (ostream& os, MyBoard& board);
bool Empty ();
// is everything already good? is the board already empty?
bool North ();
// to raise the board from the north;
// returns true if none of the balls hit the other’s hole;
// else returns false
bool South (); // to raise the board from the south
bool West (); // to raise the board from the west
bool East (); // to raise the board from the east
};
bool operator== (MyBoard& board1, MyBoard& board2);
// compares only the arrays of the Board
// of the objects under consideration
}
Some comments have already been given in the class description itself. Implementation of the methods, apparently, is unlikely to cause interest; here, it is purely technical work.
To store arrays of positions (more precisely, pointers to positions), it is convenient to use a specially written successor of the class CPtrArray; it is important to note that this approach is desirable very often, when considering an array (or list) of pointers to a variety of data structures. So, the following description of the derived class CPtrArray is possible:
class MyArray : public CPtrArray { // of MyBoard*
public:
bool Exists (MyBoard* pBoard);
void MyAdd (MyBoard* pBoard);
};
Unlike the previously discussed MyBoard class, we shall introduce here the implementation of these methods.
bool MyArray::Exists (MyBoard* pBoard) {
for (int i=0; i<GetSize(); i++) {
MyBoard* pN = (MyBoard*)GetAt(i);
if (*pN==*pBoard) return true;
}
return false;
}
void MyArray::MyAdd (MyBoard* pBoard) {
if (Exists(pBoard)) delete pBoard;
else Add(pBoard);
}
Here, the Exists() method, by the simplest linear search, gives an answer to the question of the presence in the array of some element-position (for the possibility of such a search, we have previously reloaded the comparison operator of the MyBoard class) and the MyAdd() method adds a new position to the end of the array. If the position in question is already present in the array, then we do not add it; moreover, we call the destructor for it. Note that this approach requires accuracy (since the establishment of the object occurs at one level of the program, and its removal occurs at the other one), but it is possible.
Findings
Now consider the most important class MyTask defining our main construction, i.e. the whole task. It is very important to note that it is desirable to use almost the same class in a lot of more complicated discrete optimization problems.
class MyTask {
private:
MyArray Current; // positions not yet considered
MyArray Old; // positions already considered
public:
MyTask (MyBoard& board);
friend ostream& operator<< (ostream& os, MyTask& task);
int Step ();
// returned value:
// -1 the array of subtasks is empty;
// 0 this situation requires the continuation of the work;
// >0 the answer
int Run ();
// returned value:
// -1 there is no answer;
// >=0 the answer
};
The Run() method is of no interest: it consists of sequential calls to the Step() method; the implementation of the last one is given below.
int MyTask::Step () {
if (this->Current.GetSize()<=0) return -1;
MyBoard* pOld = (MyBoard*)Current.GetAt(0);
if (pOld->Empty()) return pOld->GetDeep();
// the "reinsurance"
this->Current.RemoveAt(0);
int nLast = pOld->GetLast();
if (nLast!=1) { // we can lift the board from the north side
MyBoard* pN = new MyBoard(*pOld);
if (!pN->North()) delete pN;
else if (pN->Empty()) {
int n = pN->GetDeep();
delete pN;
return n;
}
else if (Old.Exists(pN)) delete pN;
else this->Current.MyAdd(pN);
}
// ...
// similar challenges of lifting the board from 3 other sides;
// the texts of such calls are omitted
// ...
Old.Add(pOld); return 0;
}
Let us note, that it is possible to simplify the full search (that is, to reduce the number of positions considered) in different ways; we mean not only not reviewing the same move twice consecutively (i.e., using the nLast field). However, we will not discuss this point in more detail, we hope to return to it in the paper-continuation.
Conclusion
In the next publication, we are going to consider the continuation of this material, and to complicate it both from the point of view of the problems under consideration and from the point of view of algorithms.
As problems of discrete optimization solved by the same approach, we propose to consider the traveling salesman problem in its classical formulation (Pola´k, 2005), etc., and also the problem of minimization of nondeterministic finite automata (Melnikov, 2018), etc. Among our publications, devoted to this topic, we note once again Melnikov & Melnikova (2017), Melnikov & Pivneva (2016) and also Melnikov & Melnikova (2018) and Pivneva, Melnikov, & Kuptsov (2016). These problems (of the article-continuation) should be available to the “advanced” student.
And as the algorithms that develop this topic, we propose to consider the following. First, we note that in the above problem, we can actually not separate the matrix and the subtask that includes it; however, in more complex cases this cannot normally be done. The discussion of such an implementation (let us repeat, also available to the “advanced” young student) is assumed in the collapsing publication.
One of the auxiliary algorithms necessary for this is the division of the task into two subtasks; this division is one of the most important parts of the branch and boundary method (Melnikov & Melnikova, 2017; Melnikov & Pivneva, 2016; Melnikov & Melnikova, 2018). We carry out this division as a method of the subtask class (in our notation, MySubTask): this method changes the owner (the object of the class MySubTask), making from it the so-called “right subtask” (Cormen, Leiserson, Rivest, & Stein, 2009). As an output, it gives a pointer to the created “left” subtask, to which the constructor was previously applied.
References
- Analytical statement. (2007). The 2007 ACM Programming Contest World Finals, Retrieved from URL: https://icpc.baylor.edu/ regionals/finder/world-finals-2007. Accessed 29.09.18.
- Cormen, T., Leiserson, Ch., Rivest, R., & Stein, C. (2009). Introduction to Algorithms. Boston, US: MIT Press.
- Hromkoviˇc, J. (2011). Theoretische Informatik: Formale Sprachen, Berechenbarkeit, Komplexittstheorie, Algorithmik, Kommunikation und Kryptographie. Berlin, German: Springer Verlag.
- Lipski, W., (2004). Kombinatoryka dla programisto´w. Warszawa, Polish: Wydawnictwa Naukowo-Techniczne.
- Luger, G. (2008). Artificial Intelligence: Structures and Strategies for Complex Problem Solving. Boston, US: Addison Wesley.
- Melnikov, B. (2017). The complete finite automaton: International Journal of Open Information Technologies, 5(10), 9-17.
- Melnikov, B. (2018). The star-height of a finite automaton and some related questions: International Journal of Open Information Technologies, 6(7), 1-5.
- Melnikov, B., & Melnikova, A. (2018). Pseudo-automata for generalized regular expressions: International Journal of Open Information Technologies, 6(1), 1-8.
- Melnikov, B., & Melnikova, E. (2017). Waterloo-like finite automata and algorithms for their automatic construction: International Journal of Open Information Technologies, 5(12), 8-15.
- Melnikov, B., & Pivneva, S. (2016). On the multiple-aspect approach to the possible technique for determination of the authors literary style. The 11th International Scientific-Practical Conference Modern Information Technologies and IT-Education: CEUR Workshop Proceedings. Selected Papers SITITO 2016 (pp. 311-315). Moscow, Russia: Creative Commons CC0
- Pivneva, S., Melnikov, B., & Kuptsov, N. (2016). Infinitely complex sum of classification of non-commuting matrix S-sets. In The 1st International Scientific Conference Convergent Cognitive Information Technologies: CEUR Workshop Proceedings. 1. Сер. "Selected Papers of, Convergent 2016" (pp. 56-63). Moscow, Russia: Creative Commons CC0
- Pola´k, L. (2005). Minimizations of NFA using the universal automaton: International Journal of Foundations of Computer Science, 16(5), 999–1010.
- Russel, S., & Norvig, P. (2010). Artificial Intelligence: A Modern Approach. NJ: Prentice Hall.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
20 March 2019
Article Doi
eBook ISBN
978-1-80296-056-3
Publisher
Future Academy
Volume
57
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-1887
Subjects
Business, business ethics, social responsibility, innovation, ethical issues, scientific developments, technological developments
Cite this article as:
Melnikov, B., Melnikova, E., Pivneva, S., Soldatov, A., & Denisova, D. (2019). Computational Problems For “Advanced” Younger Students. In V. Mantulenko (Ed.), Global Challenges and Prospects of the Modern Economic Development, vol 57. European Proceedings of Social and Behavioural Sciences (pp. 1316-1325). Future Academy. https://doi.org/10.15405/epsbs.2019.03.133

