Computer Games As A Tool For The Development Of Algorithmic Thinking

Abstract

The purpose of the study is to identify whether a playing computer games that have their own rules and winning strategy develop algorithmic thinking of players. Several questions pertaining to whether a computer game user can express game rules as an algorithm, whether playing didactic computer games can develop the algorithmic thinking of a player, or whether computer games and their playing is motivational enough for students to learn programming so they could create their own computer games were considered for investigation. There was also interest in whether students can use their knowledge from playing computer games to creating their own. This included the concern about their implementation of increasing difficulty, evaluating player’s performance or archiving results. Another point of interest was how students dealt with possibility to pause the game, resuming its state and continuing playing the game, option to change the number of players or whether the application contains playing or even winning strategy etc. An experiment was carried out among students of selected teacher training faculties in Slovakia to examine whether students solved game situations using algorithms to developing a winning strategy. Based on results of the study project-based and problem-based education were implemented into programming classes for future teachers of computer science with goal set to gamification of education, so teaching programming would be fun and learning could become a game.

Keywords: Computer gamesalgorithmical thinkingteacher training

Introduction

Use of computers and digital devices is a daily necessity in the lives of pupils and students. They use mobile devices not only for communication, acquiring information, learning, using different services, but also for relaxation and playing. Studies has shown that children, youngsters and students spend a significant amount of time playing computer games while working with a computer. Computer games aren’t despised even by adults and seniors, where in case of their favorite relaxation activities like desk games: checkers, chess, mill etc., card games: patience, solitare and other games that are implemented on a computer an opponent, partner or a companion is played by a computer (Chráska, 2016; Chráska & Basler, 2016). A computerised version of a game usually contains not only monitoring whether game is played by the rules but also certain player’s strategy which can lead to winning or a good performance of a computer in a role of an opponent. That is why didactic computer games were implemented in programming classes where logical and programming thinking is essential. This implementation of chosen didactic games (Stoffová, 2016a; Dostál, 2009) can be considered a good topic to check whether a student has mastered basics of algorithmizing and programming and whether he is able to create software individually or in a team (Kožlej, 2018; Végh, 2017)

Every informatics (computer science) teacher educational program contains several classes oriented on algorithms and programming. Absolvent profile shows that every teacher of informatics should master all informatics subjects which are being taught in elementary schools and high schools. He has to constantly update content of these subjects, innovate them and use adequate modern and effective methods and technologies in teaching. He/she should therefore be not only a good specialist, but also a good teacher who motivates, encourages, makes students more active, knows how to raise interest in the subject he teaches but also knows how to maintain and increase curiosity and interest in acquiring knowledge and skills needed in a given subject. Programming dominates among fundamental informatics subjects.

Computer Games in Algorithms Creation and Programming

Students wishing to become informatics teachers will encounter first algorithm in the first semester of Algorithms and programming class. It’s a type of algorithm that isn’t based on mathematical methods of solving a problem. Algorithms besides making sure that rules are being followed also contains a winning strategy. It should serve as a motivation mainly for students of informatics teaching program, who don’t study mathematics as their secondary approbation subject (Basler & Dostál, 2016). Algorithms are not only used as a process of solving mathematical, technical or economic problems, but also to show how to solve game situations, language problems and even problems from various parts of everyday life (Basler, 2016; Chráska, 2016ab). Even those who do not like mathematics can became good programmers, creators of effective software applications and also good teachers of informatics. The most simplified version of a game (named NIM) is as follows. Two players are playing the game (one of them is a computer). At the beginning they have a pile of matches available with quantity of N. Players take turns to remove the matches in quantity of <1-M>. The player who takes the last match, loses. Players decide who will start the game. It’s not a problem to construct an algorithm that manages the game which monitors following of the rules and realizes its own turn. The computer therefore realizes its own turn by generating a random number from the <1-M> interval. After that a player’s turn follows and computer checks whether player doesn’t want to take more matches than M, or more than there are matches on the pile in a given moment. After every correct turn the computer checks whether remaining matches doesn’t equal one, or whether the player, whose turn it is, didn’t take all the matches on the pile. At that moment it ends the game and declares who has won and who has lost. What is interesting is whether a winning strategy exists and whether a player (computer) controlled by a program can actually win. A closer analysis of the game and its rules will reveal that the game has 3 parameters (input data), that serve for defining starting state and defining the game state. They are: N, M, and who starts the game. If computer has only one parameter (input value for a program) for itself, then it is possible to build a winning strategy into the program. For example, if the player sets 2 parameters: M and who starts, then a computer can calculate N (starting quantity of matches), so it can defeat the player. In a situation when the M and who starts (in case when the play start the player) is set, N = (M+1)*RN + 1 (RN is a random number that indicates the number of turns, one turn is player’s and computer’s one step combined). Then it’s enough for a computer to always draw (M-NP), where NP is number of matches that were drawn by the player. In a case where M is given and a computer starts the game N = (M+1)*RN + 1 + NC (NC is a random number from the <1-M> interval, which is number of matches that is removed at the beginning, namely in the first turn). The detailed description of this algorithm can be found in the textbook (Stoffová & Czakó & Végh, 2015).

A simple computer game for creating sorting algorithms, winning strategy and development of algorithmic thinking can be used. In this game, the player’s task is to sort boxes. The game has 3 levels of difficulty depending on number of boxes that need to be sorted. The player has a double weight scales available for sorting boxes from the lightest to the heaviest. The task for the player is to put the boxes on hooks. The player has to be careful, so he/she does not put heavier box that it can bear on any hook. It is necessary for a player to use the scale as seldom as possible to get better results. Weights of boxes in the first level are 1, 2 and 3 kg. In the second level the number of boxes is five. Finally, in the third level of the game the player’s task is to sort seven boxes. Using simple “linear” sorting algorithms and their combination it is not possible to get better results than algorithms with complexity of O (n²). Gradually improving the process of solving the task, the player will get to work his way to algorithms with complexity of O (n*logn) e.g. to Quicksort. This game is also a good example of didactic computer game which is the topic of semester thesis of students at the end of second semester.

The website http://ani.ide.sk/ can be referred to, to understand how different sorting algorithms work where there is whole set of visualized algorithms, from simple to complex one, presented. Whole group of animation-simulation models of sorting different objects (cards, bars, etc.) demonstrates (very often in playful funny way) how sorting algorithms work. Many of the simulation models are just visualization of the sorting processes, while others allow certain interaction from the user (Pšenáková, 2016). It’s a suitable didactic application for demonstrating how sorting algorithms work implemented in programming language Delphi (Figure 01 ).

See Full Size >

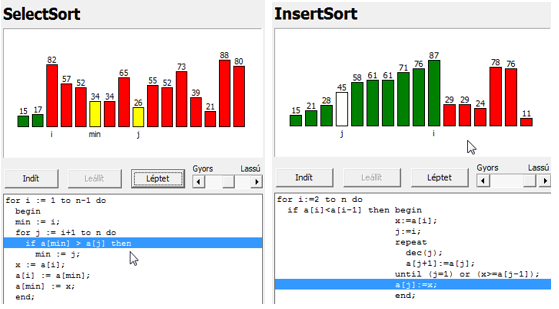
For deeper analysis of sorting algorithms and discovering of their properties this application was specifically used. Besides visualized graphic model it also contains written algorithmic code. Line cursor shows which part of an algorithm is being currently executed in the source code. It allows a learner to analyse 5 basic sorting algorithms: Simple Sort, Select Sort, Bubble Sort, Insert Sort and Quick Sort. The user can study the source code, compare algorithms between each other, search for differences among them and discover their properties which he can then use for writing his own program codes (Végh, 2017; Végh & Stoffová, 2016, 2017). The student’s task was to at first understand how individual sorting algorithms work, comment source (pseudo)code and verbally describe and express in writing every algorithm based on visualized simulation experiments with a model. His task was also to explicitly express sorting state in defined moment when the sorting animation stopped (so express it in certain values of control variable cycles). Students were also given task to discover informational meaning of sorted object’s colour. Objects of sorting were columns of various (random) height. Columns weren’t sorted at the beginning.

Problem Statement

Didactic computer games are a powerful motivational tool; it develops not only algorithmic, logical and programming thinking of students, but also creates basis for application of playful way of teaching in their future educational practice. However, despite its many educational benefits, this particular branch of education is not well explored. This study attempts to uncover information that will help to extend this field of educational knowledge.

Research Questions

This research that has been conducted since 2010 at teacher training faculties of Slovak universities, has been oriented on the influence of gaming and creating didactic computer games and playful illustrative form of teaching for development of algorithmic thinking of students. The study intends to answer the following questions: Can a computer game user (and creator) express game rules as an algorithm? Can playing didactic computer games develop the algorithmic thinking of a player? To find answers, open and also closed questions and tasks were used.

Purpose of the Study

The purpose of the study is identify whether a playing computer games that have their own rules, develop algorithmic thinking of players. An experiment was carried out among students of teacher training faculties in Slovakia where students were investigated as they participated in solving game situations using algorithms to developing a winning strategy. Another purpose of the study was to find out how the use of visualized animation simulation models in education to increase students' knowledge in algorithms and programming. Based on the analysis of solved tasks expressed in text form and the determination of their degree of accuracy, students were divided into several groups. The solution of the tasks expressed in text form helped us to assemble a knowledge test with closed questions, which could be easily evaluated.

Research Methods

To obtain the answers to the research questions listed in section 3 various questionnaires and knowledge tests with open and also closed questions and tasks were used. Tasks with the open solution required students to express an algorithm – process of solving the gaming task. In a case of a computer game based on sorting boxes with the lowest number of comparisons, the task was to verbally describe the process of solving the problem. Players had to repeat the game until he solved the problem without any unnecessary repeating the measurements. (See figure 02 ). The player had the opportunity to repeat the game in a case he didn’t remember the process. During the game he figured out that he is following a certain algorithm and that he is using a certain game strategy.

See Full Size >

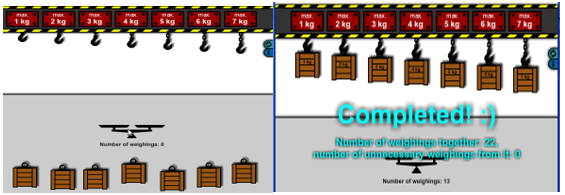
Unrestricted verbal description of the process of solving the problem was usually correct, but it was not always complete and precise. While identifying and analyzing the process of solving the problem we have found out that the students at first used simple linear sorting algorithms with quadratic difficulty (O (n²) and then gradually started using algorithms with difficulty of O (n*logn), or that they have used their combination respectively. Students had problems with expressing the solving process by using the source code and they were only seldom able to debug their program.

In the next phase of teaching, visualized simulation models were used, most of which can be found on the website ide.sk and also other own educational software supported the gamification of learning. These were considered useful: in which source code was shown together with the sorting animation, as pointed out in section 3 of this paper.

Using the questionnaire method, it was discovered whether students understood how individual algorithms work, what are differences between them, which of those can be used for optimization of the program. Respondents were informed that the data from filled out questionnaire will be used for improving the learning and increasing its quality. That’s why they were asked to answer honestly “from the heart” as research ethics were strictly observed and data would only serve as a criteria for evaluating and comparing the results from the questionnaire. They wrote their answers directly into the electronic questionnaire. Range, depth and length of the answers wasn’t limited in any way and the respondent could use as many lines as he/she needed to express his/her opinion on a given question.

Besides a few personal data, the questionnaire contained group of questions oriented on evaluating the didactic application and determining its value for teaching and learning process. Respondents have rated the quality of the application. They answered questions like whether the teaching aid is a suitable didactic tool, whether the application has helped them to understand individual algorithms, whether it is interactive enough, whether the controls are intuitive enough, whether the illustrative rate of the application was sufficient and whether they would recommend such teaching tools in the education process. They wrote their answers into the 6-point scale.

The general task was: Characterize, describe (based on your observations) how the individual algorithms work and what are their properties. It’s up to you how detailed it will be – you have enough time and space.

The application presented following algorithms: Simple sort, Select sort, Bubble Sort, Insert sort and Quick sort. Considering that in the pre-research the description of algorithms was open and not very complex, it was difficult to evaluate complexity of the solution, so we have guided the respondents to everything a task solution should contain. We asked them explicitly to solve these tasks for given algorithms:

• Briefly describe the working principle of the algorithm as you have observed and understood it based on the animations during the simulation experiments.

Briefly describe (in your own words) the algorithm’s properties as you have discovered them during animations. (Comment on the length of the sorted/unsorted part in individual phases of the sorting process, how cycles were controlled, how many times they were repeated, if statement on when the cycle should stop, algorithm difficulty, etc.).

• Estimate the time (in minutes) that you have devoted to understanding the algorithm.

If there was unlimited amount of time for filling out the questionnaire, when students answered the questions during their preparation for an exam for example, the answers were current and detailed enough.

Results from evaluation of time required for students to understand the algorithm were interesting.

For linear sorting algorithms like Simple sort, Select sort, Bubble Sort and Insert sort respondents have stated values from the interval of (2 - 30) minutes. In a case of Quick sort sorting algorithm, it was an interval of (5 - 45) minutes.

Solutions expressed in the verbal form (in written form) of the expressed algorithm was difficult to evaluate. Using the analysis of content of 94 filled-out questionnaires by the students of informatics teaching program from the last 4 years, the answers were categorized according to the tasks from the questionnaire into 5 groups; answers that were: 1^st complete and correct, 2^nd correct and incomplete, 3^rd partly correct and incomplete, 4^th mostly incorrect and 5^th incorrect algorithms. We can state that no answer was sorted into 4^th and 5^th groups. Only 8 (8.5%) answers fell in the 1^st group, the 2^nd group was the largest with 64 (68.1%) and 22 (23.4%) answers fell in the 3^rd group.

Knowledge tests for verification of the effectiveness of didactic computer games and interactive visualized animation-simulation models were constructed. The knowledge of the students from the area of sorting algorithms before and after using these didactic software tools were evaluated. The knowledge test contained the following 7 statements.

• The algorithm always compares two neighbouring elements in the array.

• The algorithm compares every element with all elements located behind it.

• First, the algorithm chooses one element from the unsorted part; next, the algorithm exchanges the selected element with the first or last element of the unsorted part.

• In the unsorted part of the array, the smallest element is always moved to the beginning (the sorted sequence is starting to form in the beginning of the array).

• In the unsorted part of the array, the largest element is always moved to the end of the sorted sequence is starting to form in the end of the array).

• Elements in the sorted part of the array (in the beginning or the end of the array) are not modified (not moved) during the sorting.

• Elements in the sorted part of the array (in the beginning or at the end of the array) can be modified (moved) during the sorting.

The student should indicate whether the statement is true for sorting algorithms: Simple sort, Select sort1 (MinSort), Select sort2 (MaxSort), and Bubble Sort.

Findings

Students had different knowledge about the sorting algorithms; therefore they were asked to fill out a pre-test before the experiment. Students had to decide which statement-algorithm combinations are true. Because there were students with no previous knowledge about the sorting algorithms, they were asked to mark only those answers in both tests they knew, thus, diminishing the number of students’ guesses. Next, students had time to experiment with the game-based animations and fill out a post-test. The results are shown in the figure 03 .

The first part of figure 03 shows accrual of correct answers/correct assertions and the second part of figure 03 shows decrease of incorrect answers/assertions which concerned individual sorting algorithms based on their basic functioning principles.

To determine, if these changes are significant, several paired sign tests were constructed; specifically chosen sign tests instead of paired-samples tests because the assumptions of the latter tests were violated – the data were not normally nor symmetrically distributed.

First, the increase in the correctly marked true algorithm-statement combinations was measured. Of the 92 participants involved in the experiment, 81 students marked more true algorithm-statement combinations, 5 students marked less true algorithm-statement combinations, and 6 students marked the same number of algorithm-statement combinations in the post-test compared to the pre-test. Overall, participants marked more true algorithm-statement combinations in the post-test (median: 11 marks) than in the pre-test (median: 7 marks), the statistically significant increase in the median of the differences is 4 marks, z = 8.087, p < 0.0005.

See Full Size >

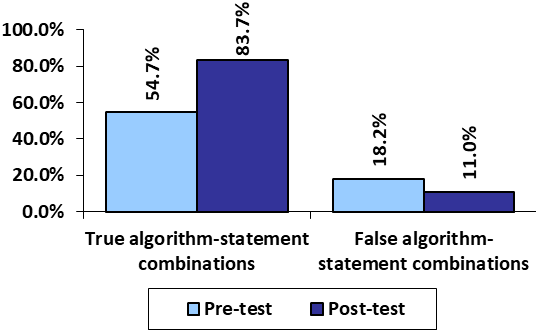
The decrease in the incorrectly marked false algorithm-statement combinations was also measured. Of the 92 participants involved in the experiment, 61 students marked less false algorithm-statement combinations, 23 students marked more algorithm-statement combinations, and 8 students marked the same number of algorithm-statement combinations in the post-test compared to the pre-test. Overall, participants marked less false algorithm-statement combinations in the post-test (median: 2 marks) than in the pre-test (median: 4 marks), the statistically significant decrease in the median of the differences is 1 marks, z = 4.037, p < 0.0005.

After these positive results, the students’ answers were examined more deeply separately for every sorting algorithm in the pre-test and post-test.

In the post-test, the number of signed correct statements for each listed sorting algorithm was higher than in the pretest, and the number of signed misstatements decreased.

Conclusion

The researcher’s experiences and results of the research show that playing suitable didactic games can be a source of spontaneous acquisition of new knowledge. Selected didactic games were tested to determine whether playing them contributes to the development of the algorithmic and strategic thinking of the player. It may be assumes that each player develops their own winning strategy while solving their game situations, which they will gradually improve and optimize until they reach the optimal solution.

Based on the analysis of selected didactic game, its rules can be defined as the didactic value of the game. Based on optimal solutions of gaming tasks advice to teachers can be formulated in the way that playing has a didactic benefit for achieving the educational objectives.

Didactic computer games are a powerful motivational tool, they excite the attention of pupils and students and they keep it for a longer time than the teacher would be able to keep it in a common didactic situation (Stoffová, 2018). Students’ knowledge is deeper and more permanent when they acquire it through their own experience while employing the principles of a constructivist theory of learning. Students and pupils are playing computer games voluntarily and they do not realize that they are learning.

Creating of computer games is a good topic for problem-based and project-based teaching of algorithmizing and programming at every degree of education system. It is extremely useful for students of informatics teaching program. It develops not only algorithmic, logical and programming thinking of students, but also creates basis for application of playful way of teaching in their future educational practice

Acknowledgments

The paper was supported by project Palacký University Olomouc IGA_PdF_2018_030 “An analysis of the use of educational computer games and online educational courses in secondary schools in relation to potential addictive behaviour in students in relation to gaming”.

References

1. Basler, J. (2016). Počítačové hry a způsob jejich využívání u žáků základních škol. Trendy ve vzdělávání, 9(1), 10-19.
2. Basler, J., & Dostál J. (2016.) Analysis of studies focused on research of computer games’ influence with an accent on education and people’s psychics. In: ICERI2016 Proceedings. Seville, SPAIN: 9th International Conference of Education, Research and Innovation, s. 33-40.
3. Chráska, M. (2016a). Computer Games – Preferred Way of Using ICT by Grammar School Students. The European Proceedings of Social & Behavioural Sciences, 606–616. https://doi.org/10.15405/epsbs.2016.11.63
4. Chráska, M. (2016b). Grammar School Students and Their Typology According to Dependence on Computer Games. In SGEM 2016 Conference Proceedings. Sofia: STEF92 Technology Ltd., pp. 795–802. https://doi.org/10.5593/SGEMSOCIAL2016/B11/S03.101
5. Chráska, M. (2016c). Žáci gymnázia a míra jejich závislosti na počítačových hrách. Trendy ve vzdělávání, 9(1), 110-114.
6. Chráska, M., & Basler J. (2016). Research of Computer game addiction among the 18-year- old students of general upper secondary schools in the Czech Republic. In: ICERI2016 Proceedings. Seville, SPAIN: 9th International Conference of Education, Research and Innovation, s. 69-78.
7. Czakóová, K. (2016). Creation small educational software in the micro-world of small languages. In: Teaching Mathematics and Computer Science. 14(1), 2016/1, 117. Debrecen : University of Debrecen.
8. Czakóová, K. (2016). Tvorba vlastných aplikácií v Imagine. In: Úvod do programovania v prostredí mikrosvetov : vysokoškolská učebnica. Komárno : Univerzita J. Selyeho, 2016. 34-55.
9. Dostál, J. (2009). Výukový software a didaktické počítačové hry - nástroje moderního vzdělávání. Journal of Technology and Information Education, 1(1), 24-28.
10. Horváth, R., & Stoffová, V. (2016) The Graphical support for the didactic games creation. In: XXIXth DIDMATTECH 2016: New methods and technologies in education and practice :2nd Part. Ed. V. Stoffová, L. Zsakó, 1. vyd. Budapest: Eötvös Loránd University in Budapest: Faculty of Informatics, 2016, s. 67-82.
11. Koreňová, L. I., & Veress-Bágyi, I. (2017). A kiterjesztett valóság alkalmazása az általános iskolai matematika tanulásban (Inquiry-Based Mathematics Learning by Applying Augmented Reality in the Primary School). In: XXXth DidMatTech 2017: New Methods and Technologies in Education and Practice: 2nd part. Ed. V. Stoffová a R. Horváth. 1. vyd. Trnava: Trnava University in Trnava, Faculty of Education, 75 – 86.
12. Kožlej, J. (2018). Didaktické počítačové hry v projektovom a problémovom vyučovaní programovania. [Bakalárska práca]. – Trnavská Univerzita v Trnave. Pedagogická fakulta; Katedra matematiky a informatiky. - Vedúci: Prof. Ing. Veronika Stoffová, CSc., 2018. 58 s.
13. Lapšanská, Š. (2018). Animačno-simulačné modely na podporu vyučovania základov algoritmizácie a programovania, Diplomová práca, Trnavská univerzita v Trnave, Pedagogická fakulta, Katedra informatiky. Vedúci diplomovej práce: prof. Ing. Veronika Stoffová, CSc. Trnava: Pedagogická fakulta TU, 2018, 72 s.
14. Pšenáková, I. (2016). Interactive applications in the work of teacher. In XXIXth DidMatTech 2016. Budapest: Eötvös Loránd University in Budapest, Faculty of Informatics, pp. 92–100. Retrieved from https://www.mii.lt/informatics_in_education/htm/infedu.2017.07.htm.
15. Stoffa, V., Czakó, K., & Végh, L. (2015). Programozás a gyakorlatban: Algoritmizació és progrsamozás II. (Programovanie v praxi) Komárom: Selye János Egyetem Gazdaságtudományi Kar, 2015. 1. vyd. 124 s.
16. Stoffová, V. (2016a). Počítačové hry a ich klasifikácia. Trendy ve vzdělávání, 9(1), 243-252.
17. Stoffová, V. (2016b). The Importance of Didactic Computer Games in the Acquisition of New Knowledge. European Proceedings of Social and Behavioural Sciences,16, 676-688.
18. Stoffová, V. (2018). Didactic computer games – a playful form of teaching and learning. In: Education & Educational Research (in press)
19. Végh, L. (2016). Javascript library for developing interactive micro-level animations for teaching and learning algorithms on one-dimensional arrays. Acta Didactica Napocensia, 9(2), 23–32.
20. Végh, L. (2017). A programozás tanulásának és tanításának támogatása elektronikus tananyagba beépíthető interaktív animációs modellekkel. (PhD theses). Eötvös Loránd Tudományegyetem Informatika Kar, 2017
21. Végh, L., & Stoffová, V. (2016). An interactive animation for learning sorting algorithms: How students reduced the number of comparisons in a sorting algorithm by playing a didactic game. In: Teaching Mathematics and Computer Science, 14(1), 45–62. Institute of Mathematics – University of Debrecen.
22. Végh, L., & Stoffová, V. (2017). Algorithm Animations for Teaching and Learning the Main Ideas of Basic Sortings. In: Informatics in Education, 16(1), 121-140. https://doi.org/10.15388/infedu.2017.07