Abstract
A problem in Strategic Human Resource Management about evaluation of the impact of a training programme on performance has been faced in the case of areal spatially referred data. Generalized log-linear Poisson models with and without spatial component (with Besag specification) have been considered and compared. A Bayesian modelling approach has been adopted in the statistical data analysis. In order to avoid computational slowness of Markov Chain Monte Carlo simulations, the Integrated Nested Laplace Approximation method has been used in model fitting. It has been shown that the spatial structure, when considered, may improve the identification of the real drivers of performance. It follows that investigating hidden spatial structure in the data set should be a good practice when using data analytic tools in Strategic Human Resource problem solving. The interactions and interplay between areas and customers who live and act in geographically adjacent districts should be always considered in model fitting;
Keywords: Human resourcetraining programmespatial structurebayesian statisticINLA
Introduction
Companies cannot be competitive without good and trained people, and people are the very asset of companies. The return of well oriented investments on people may manifest itself in a very advantageous way (Sesil, 2013).
One of the key tasks of Strategic Human Resource Management could be an intervention aimed to impact some aspect of employee behaviour. It may happens that the intervention consists in the introduction of new sales tecniques and of a related training programme, and its goals is the improvement of the employee performance, measured in some way. Since any training activity may involve a considerable financial investment, any HR function should evaluate its potential return. In order to gain the increase in competitiveness that the training programme may offer, first the outcomes as part of a business case should be presented for approval. The evaluation process of the efficacy of a training programme aimed at improving employee performance should consider that several aspect and variables may impact the latter (Fitz-enz & Mattox II; 2014). If the goal of the training programme is an improvement of performance, it is important to quantify in the right way the amount of the eventual gain that can be attributed to each measurable variable and in particular the part due to the programmed intervention.
It is a diffuse and well known practise to evaluate the dependency of a measurable outcome of interest on some measurable variables, and to identify which variables really drive the output, by a regression model. When the response of interest is a counting variable, a Poisson regression model may be a preferable choice. It is one of the so called Generalized Linear Models (GLMs) originally formulated by McCullagh and Nelder (1989). A GLM is a generalization of the Normal linear model of classical regression allowing for response variable with a distribution other than Normal and link function other than identity. It may also happens that the outcome of interest is geographically referenced, that is each of its values is related to a known part of a spatial region, identified by its location. These kind of data, in the statistical literature, are called
The aim of this study is to show that to be unaware of the spatial structure underlying the data can lead to wrong results and wrong identification of the relevant drivers of performance. The data considered concern the number of sold units, thought as a measure of performance, for each year (from 2008 to 2015) and for each of 32 London boroughs. Each boroughs is assigned to a sales manager. In the summer 2011 a voluntary training programme was proposed to sales managers aimed to improve performance by new customers’ approach and sale techniques.
A Bayesian modelling approach has been adopted in the statistical data analysis. Bayesian models assume that model parameters are randomly distributed. From the computational point of view, Bayesian modelling is usually much more difficult than Frequentist modelling. To compute the parameters’ probability distributions, some variation of the Markov Chain Monte Carlo (MCMC) method of simulation is usually adopted. MCMC calculations are relatively slow as a computational method. Even for simple models, the ability to quickly fitting models to data is crucial in explorative data analysis as well as in statistical modelling in general. A new method for fitting Bayesian models has been used here: the Integrated Nested Laplace Approximation (INLA). As an approximation method INLA is more than adequate with results usually practically identical to MCMC, but obtained in a very faster way.
All the statistical analysis and graphs in this paper have been carried out with the statistical software R (R core team, 2017) and some of its packages. We have taken advantage of the use of the
Literature Review and Theoretical Framework
In recent years, when managers interrogate and analyse data before making strategic decisions, HR analytics represents a growing trend and expanding research area. Several books have recently been published in the field of HR analytics. Fitz-enz and Mattox (2014) is a how-to guide to predictive analytics for Human Resources, filled with practical and targeted advice. It starts with the basic idea of engaging in predictive analytics and walks through case simulations showing statistical examples.
Sesil (2013) shows how to apply advanced analytics to bring objectivity to decision making, and improve employee selections, performance management, strategy alignment and more. Edwards and Edwards (2016) may help inquisitive HR professionals and students to understand, acquire and develop the main competencies needed in the emerging field of HR analytics. Among other things, Marr (2018) shows how data can contribute to organizational success also driving performance. He covers all key elements of data-driven HR, including performance management.
Bayesian methods are increasingly used in theoretical and applied statistics. A comprehensive book on the subject, between other, is Gelman et al., (2013). Lee, Rushworth, & Napier, (2018) present the first dedicated software package for Bayesian spatio-temporal areal unit modelling with conditional autoregressive priors, based on Markov Chain Monte Carlo (MCMC) simulations.
Integrated Nested Laplace Approximation (INLA) is a very recent approach to Bayesian modeling based on advanced tools from the theory of stochastic processes. It is particularly advantageous from a computational point of view, with respect to traditional MCMC simulations (Rue, Martino, & Chopin, 2009; Rue et al., 2017). INLA has a computationally efficient implementation in the R-package R-INLA and has been widely used in practice. A clear and accessible reference for application of R-INLA method to spatial and spatio-temporal Bayesian model is Blangiardo and Camelletti (2015). A very recent review paper on spatial Bayesian modelling with INLA and the R-software is Bakka et al., (2018). In this paper we have benefited from the use of the methods introduced in (Wang, Yue, & Faraway, 2018).
Research Method
In this section we present the data set and the statistical models considered.
The Data
The time period under study comprises 8 years from 2008 to 2015. In the summer of 2011, a company’s HR management has introduced a special training programme (with voluntary participation) to improve sales skills and ability to approach potential customers of sales managers. The study area consists of 32 London boroughs, each assigned to a sales manager. For each manager, the following key variables have been measured:
The Statistical Model
The observed output
where the mean is defined in terms of the rate and the expected number for each specific areal unit. plays the role of an offset in the model and is a known quantity for each areal unity that should not be estimated. For more information about ways for computing the interested reader are referred to Congdon (2017), Elliott et al., (2000), and Lesaffre and Lawson (2012).
In the first considered model, from now on called
The log link is the natural choice for the Poisson model. The
’s are the regression coefficients of the linear effect and
is the unknown function of the nonlinear effect in
To take into account the spatial piece of information, in a second considered model,
where
is a vector identifying each of the 32 London boroughs. We take a
The two considered models,
A third model,
where the mean is defined in terms of the rate and the expected total number for each specific areal unit for the four considered years after training. A log link with additive structure is specified:
where the log rate is a linear function of , (Mean Proportional Sales before training) and their interaction. An unknown function of the spatial effect with Besag spatial structure has been also added to the model.
The Besag Spatial Model
Our data set presents an
A Gaussian increment is defined between neighbouring regions (regions that share a common border)
where and are the centroids of the regions and are the positive and symmetric weights.
Assuming the increments are independent, it can be shown that the full conditional distribution of is normal:
.
This prior is called
More specific or complex spatial structures can be adopted, such as the
The DIC and WAIC
Model comparison have been based on DIC and WAIC. DIC stands for Deviance Information Criteria (Spiegelhalter, Best, Carlin, & Van der Linde, 2002). It is a score assigned to a model that take into account how good is the model fit and the effective number of parameters, that is the complexity of the model. The less the DIC the best the model. WAIC stand for Watanabe-Akaike Information Criteria (or Widely Applicable Information Criteria) and it has been introduced in Watanabe (2010). In some sense, WAIC is an improvement of DIC (Gelman et al., 2013), but for simple models they give very similar scores.
Findings
In this section the results of the statistical analysis are presented and interpreted.
Results of preliminary Explorative Data Analysis.
In the preliminary Explorative Data Analysis no outlier where found in the data set. From the comparative violin plot in Figure
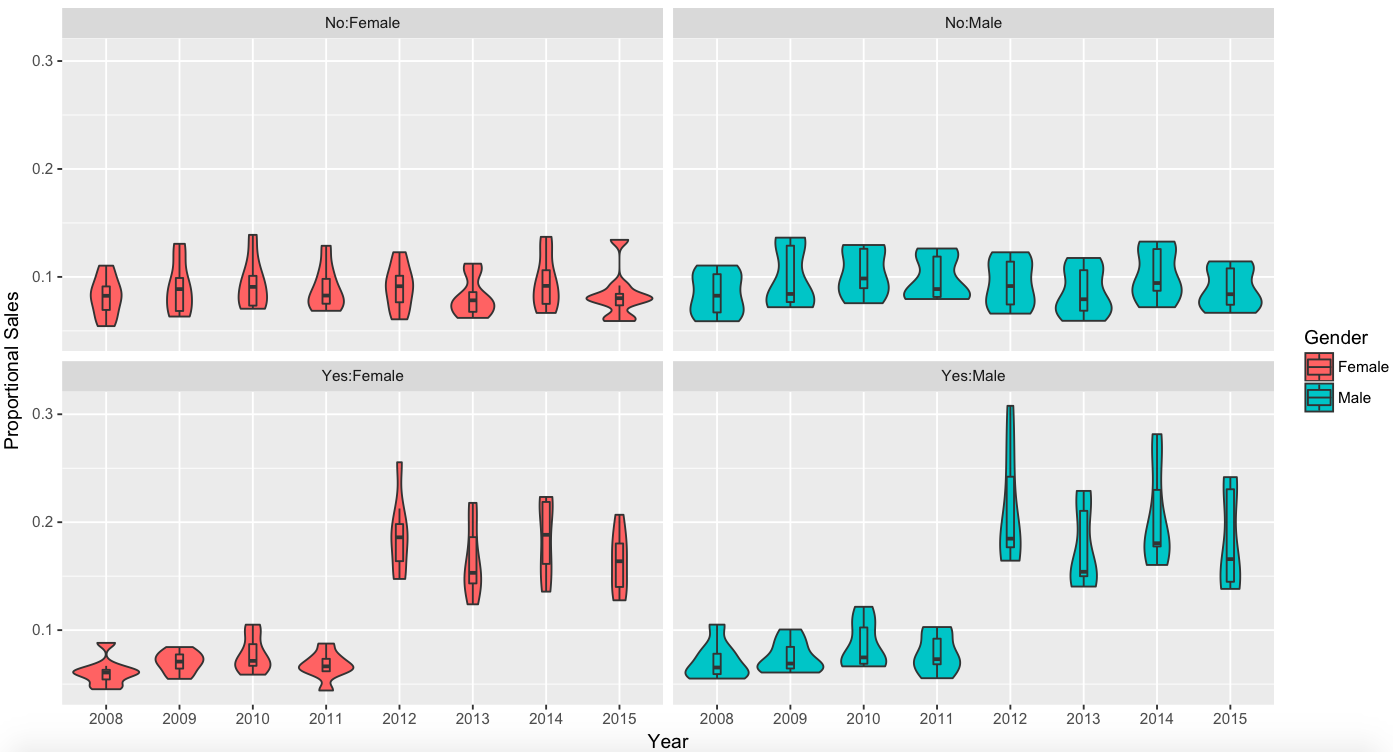
Results of the Bayesian Statistical data analysis.
Instead of MCMC simulations, the INLA approach used in this study provides approximations to the posterior marginal distributions of the parameters. Summaries of these posterior distributions include posterior means and 95% Credible Intervals (CI), which play in Bayesian statistics the same role of the maximum likelihood estimates and 95% Confidence Intervals in classical Frequentist statistics.
The estimated distribution of the parameters of
From the results of
In model comparison, (DIC=4619.337, WAIC=5038.290) appears to be better than (DIC=6468.970, WAIC=6673.552).
Maps may be a very useful tools for representing areal data. In Figure
The estimated distribution of the parameters of
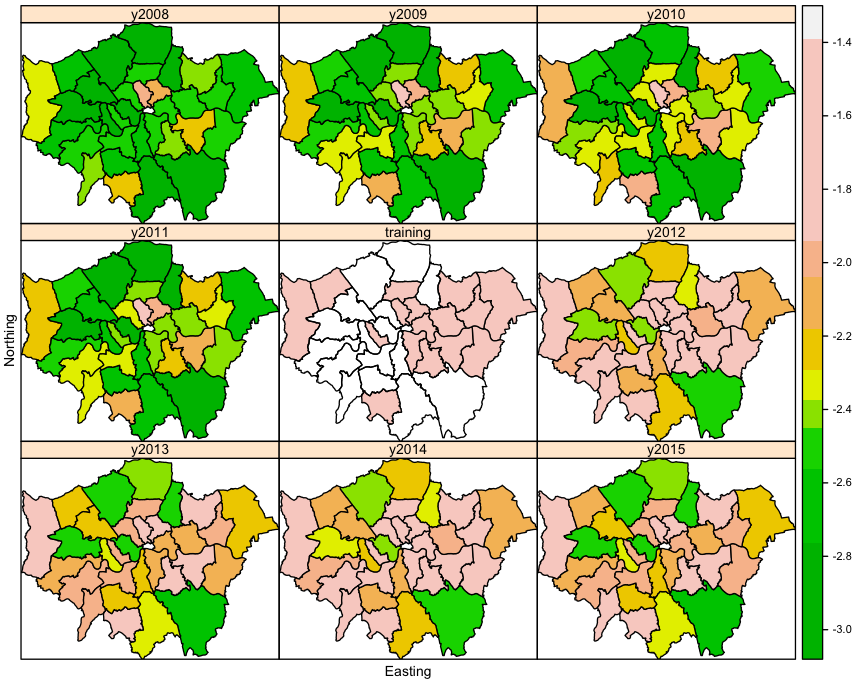
Conclusion and Discussions
In field such as econometrics and social science, as well as in epidemiology, it is very common to deal with data set whose observations are referred to contiguous non-overlapping areal units. In this case we talk of areal unit data, a special type of spatial data. A large suite of modelling tools has been developed for analysing this kind of data structure with a Bayesian approach. The aim of this study was to show that in a typical investigation in Strategic Human Resource Management it might be very important to take into account the spatial structure of data. A problem of evaluation of the impact of a training programme on the sales managers’ performance has been faced. The analysed data set is composed of areal unit observations referred to 32 London boroughs. It has been shown that if the spatial structure is not taken into account in the model fitting, results can be misleading and some irrelevant covariate may be wrongly considered a relevant driver of the outcome of interest.
We have first considered a model without considering the spatial component. In this model covariates like Age and Gender appeared to be relevant as drivers of the performance outcome. However when considering the spatial nature of our data it appeared clear that the only relevant covariate was Training, that is the training programme appeared to be the only real driver of the performance gain.
It should be a good practice, when applying data analytics in Strategic Human Resource Management, to pay attention to a possible spatial structure hidden among the data to be modelled. If the goal of a training programme is an improvement of performance, considering the spatial structure may help in quantifying the right amount of performance gain due to the programmed intervention. Ignoring the real data structure may lead to misleading conclusions.
References
- Arcaya, M., Brewster, M., Zigler, C. & Subramanian, S.V. (2012). Area variation in health: A spatial multilevel modeling approach. Health and Place, 18, 24-31.
- Bakka, H., Rue, H., Fuglstad, G.A., Riebler, A., Bolin, D., Illian, J., … Lindgren, F. (2018). Spatial Modelling with R-INLA: a Review. WIREs Computational Statistics, 10, 1-24. https://dx.doi.org/10.1002/wics.1443.
- Besag, J., York, J. & Mollie, A. (1991). Bayesian image restoration, with two applications in spatial statistics. Annals of the Institute of Statistical Mathematics, 43, 1-59.
- Besag, J. & Kooperg, C. (1995). On conditional and intrinsic autoregression. Biometrika, 82, 733-746.
- Bivand, R.S., Pebesma E. & Gomez-Rubio, V. (2013). Applied Spatial Data Analysis with R. (2nd ed.). New York, NY: Springer.
- Blangiardo, M. & Cameletti, M. (2015). Spatial and Spatio-temporal Bayesian Models with R-INLA. Chichester, UK: John Wiley & Sons.
- Congdon, P. (2017). Quantile Regression for Area Disease Counts: Bayesian Estimation using Generalized Poisson Regression. International Journal of Statistics in Medical Research, 6, 92-103.
- Cressie, N. (1993). Statistics for Spatial Data. New York, NY: Wiley.
- Dong., G., Ma, J., Harris, R. & Pryce, G. (2016). Spatial Random Slope Multilevel Modeling Using Multivariate Conditional Autoregressive Models: A Case Study of Subjective Travel Satisfaction in Beijing. Annals of the American Association of Geographers, 106(1), 19-35.
- Edwards, M.R. and Edwards, K. (2016). Predictive HR Analytics: Mastering the HR Metric. London, UK: Kogan Page.
- Elliott, P., Wakefield, J., Best, N. & Briggs, D., (Eds.). (2000). Spatial Epidemiology: Methods and Applications. Oxford University Press.
- Fitz-enz, J., & Mattox II, J.R. (2014). Predictive Analytics for Human Resources. New York, NY: Wiley.
- Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A. & Rubin, D.B. (2013). Bayesian Data Analysis (3rd ed.). Boca Raton, FL: Chapman & Hall/CRC.
- Lee, D., Rushworth, A. & Napier, G. (2018). Spatio-Temporal Areal Unit Modeling in R with Conditional Autoregressive Priors Using the CARBayesST Package. Journal of Statistical Software, 84(9), 1-39.
- Lesaffre, E. & Lawson, A. (2012). Bayesian Biostatistics. Chichester, UK: John Wiley & Sons.
- Marr, B. (2018). Data-driven HR. New York, NY: Kogan Page.
- McCullagh, P. & Nelder, J. (1989). Generalized Linear Models (2nd ed). London: Chapman & Hall.
- R Core Team. (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/.
- Rue, H., Martino, S. & Chopin, N. (2009). Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations. Journal of the Royal Statistical Society: Series B, 71(2), 319-392.
- Rue, H., Riebler, A., Sørbye, S.H., Illian, J.B., Simpson, D.P. & Lindgren, F. (2017). Bayesian computing with INLA: a review. Annual Review of Statistics and Its Application, 4, 395-421.
- Sesil, J.C., (2013). Applying Advanced Analytics to HR Management Decision: Methods for selection, developing incentives and improving collaboration. Upper Saddle River, NJ: Pearson.
- Spiegelhalter, D.J., Best, N.G., Carlin, B.P. & Van der Linde, A. (2002). Bayesian measures of model complexity and fit (with discussion). Journal of the Royal Statistical Society, Series B, 64, 583-639.
- Wang, X., Yue, Y.R. & Faraway, J.J. (2018). Bayesian Regression Modeling with INLA. Boca Raton, FL: Chapman & Hall/CRC.
- Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of machine Learning Research. 11, 3571-3594.
- Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. (2nd ed). New York, NY: Springer.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
28 January 2019
Article Doi
eBook ISBN
978-1-80296-053-2
Publisher
Future Academy
Volume
54
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-884
Subjects
Business, Innovation, Strategic management, Leadership, Technology, Sustainability
Cite this article as:
Giosa, M. D. (2019). Evaluating A Program On Hr With Spatially Structured Performance Data. In M. Özşahin, & T. Hıdırlar (Eds.), New Challenges in Leadership and Technology Management, vol 54. European Proceedings of Social and Behavioural Sciences (pp. 719-726). Future Academy. https://doi.org/10.15405/epsbs.2019.01.02.61

