Learning Proportions: How And When?

Abstract

Sound proportional reasoning is considered vital for both: Mathematics and Natural Sciences ( Lamon, 2007 ). Nevertheless it is a pain in the neck for most students from middle school and up. Our major goal is to teach ratios to students of primary school so, that they don’t have difficulties with them in Math and Sciences as well as in everyday life. As we implement the Cultural-Historical Theory ( Vygotsky, 1962 ) and Activity Approach ( Leontiev, 1981 ) to the practice of school education, we pay special attention to the early stages of concept formation. Our previous studies on learning ratios and proportions with middle school students ( Vysotskaya, 2014 ) brought promising results. However, we assume that moving ratio-learning to primary education is feasible and would save students a lot of trouble in middle school. We have devised a local instruction theory (within educational design research framework) for the 4th graders to test our ideas about 1) students’ actions that scaffold concept formation (we have suggested joint “co-measuring”) and 2) the context, that allows to make this type of activity meaningful for students (paint-mixing). The model of compound measure was introduced to coordinate students’ actions as they learn to control a particular ratio (shades of paint). The results of the experiment group (56 students) were significantly better, compared to the control group, regarding understanding of concentration as a ratio-based concept and dealing with it. We conclude that the actions, model and context we suggested made learning ratio in the 4th grade feasible, interesting and rewarding.

Keywords: Activity ApproachRatio-conceptPrimary School Education

Introduction

Ratio-based concepts are at the core of learning Mathematics and Science (Lamon, 2007). Density, buoyancy, concentration, velocity, pressure and other ratio-concepts are hard for students of middle and high school – as well as fractions, proportions and ratios are in Math (Hilton et al., 2013). Students, that experienced difficulties with fractions and proportions in Math, also fail when operating ratio-based concepts in Physics and Chemistry. And even those, who were good in Math, often demonstrate lack of comprehension: they use formulas, but don’t know their meaning, make mistakes, when world problems have phrasing they are not used to (Mahajan, 2005). Misconceptions and mistakes students make in ratio-related topics has been studied by different researchers (Hecht et al., 2007; Kloosterman, 2010; Siegler and Chen, 2008). Mistakes in solving “the missing-value” problem are often made, when children use additive thinking instead of multiplicative (Cramer, Post & Currier, 1993). Siegler and Chen (2008) on the other hand, suggested that mistakes with ratio values graduate from a weak understanding of separate values. As students got more experience working with different attributes, they also performed better with solving problems.

We assume that the main obstacle here is a significant deficiency of students’ number concept in its earliest form: whole numbers are not considered as ratios in elementary school. When children come to learning fractions and ratios they are focusing on the whole numbers and not on their ratio (Braithwaite & Siegler, 2018). However, it is crucial for further progress to understand a whole number as a ratio (Dole, Clark, Wright, Hilton, 2012), and in order to do it, every student has to rebuild completely his or her concept of the whole number assimilated in early grades.

Thus, our general question was whether it is possible to teach students in primary school in a way that will not lead to mistakes and misconceptions? We have devised a curriculum: a module “Inks” with a special learning materials and problem situations – and we tested it with our experimental classes (10-11 year-olds).

Problem Statement

Psychologists and curricula designers have always strived for an effective instruction that would help students to assimilate ratio-concepts. Many researches focus on the organization of the learning process and advise: guided-inquiry based teaching (Almuntasheri et al., 2016; Moli et al., 2017); authentic investigative activities (Ben-Chaim, Keret & Ilany, 2012); development of students’ argumentation (Chen et al., 2014). The aspects, which have been studied regarding the problem of teaching ratio vary greatly: strategies and rules that children use (Siegler & Chen, 2008), type of feedback they get, possibility to perform some experiments, etc. (Jansen & van der Maas, 2002; Nunes et al., 2003); opportunities to use computer simulations (e.g. Çepni & Şahin, 2012, Stott & Hattingh, 2015).

As we implement the Cultural-Historical Theory (Vygotsky, 1962) and Activity Approach (Leontiev, 1981) to the practice of school education, we pay special attention to the early stages of concept formation. That is why we aimed to devise a special introductory module to ratio-concepts, rather than to modify parts of regular Math or Science curricula dealing with ratios through formulas and explanatory texts in textbooks. Sometimes introductory curricula are designed as a compilation of fragments of high school courses, which also lacks effectiveness (Smith & Thompson, 2007).

Following the principles of Developmental Instruction (Davydov, 2008), we were to construct ratio-concepts with children rather than deliver it ready-made. At the same time we could not leave students to “reinvent the wheel”. Students were to extract ratio-concept from their own meaningful activity and our task was to organize their activity thus, it would be guided by the ratio-concept, though students don’t have it yet. It is a tricky question, which was answered by Davydov: students’ actions had to reconstruct the concept origin as it was in the history of human culture. Thus, we have devised several educational modules: each is based on a ratio-concept, and each of them is reconstructing some meaningful human activity. This article will focus on the concept of concentration embedded in the technology of paint mixing.

Research Questions

There were two questions we strived to answer.

The first was about students’ actions: What exactly are students to do – so that their operations and material they are working with will provide them with the desired concepts? We imply, that students should be able to use acquired concepts adequately and effectively in a range of tasks and real-life problems.

The second was about learning environment: How it should be organised – so it would scaffold students’ work? What contexts are appropriate? What contexts allow the problem to develop naturally and pose new restrictions and challenges on the students?

A special tool was suggested to mediate students’ actions: the compound measure. It consists of two measures – each for its own independent parameter. Students say, that the compound measure “goes along two lines”. They mean, that on the diagram, which we use to model values, the compound measure links two lines – each line for a parameter (like Multiple-batches Perspective in Ölmez, 2016). Thus the compound measure allows sharing the task between two students: each is responsible for his parameter. Their joint action we call “co-measuring”, meaning – coordinated measuring together with a compound measure.

The problem, that students solve, aim to involve them in some meaningful work. We suggest, that in the history of human technologies ratio-concepts appeared to take control over phenomena, that were dependent on two parameters (such as buoyancy, concentration, velocity…). The task that we present to our students is either to maintain the needed relative value, when the parameters are changing (for example, the same shade of paint, when some water is added), or to change it in a desired way, operating two values jointly. We suggested, that to “master” ratios means, that the child is able to mentally coordinate operations over two different parameters, that form a ratio. This way, the learning environment is to scaffold students’ work – the work, which deals with measuring parameters and coordinating operations in pairs.

It is a challenge to find contexts that would provide both: 1) working in pairs with separate parameters (that can be changed independently) and 2) making ratio visible, so that the relation between two parameters was represented by the third parameter, that can be observed, analysed and changed on purpose.

Several contexts were tested for the last decade (Vysotskaya et al., 2014):

• “Inks”: co-measuring ink and water to get the needed shade of blue.

• “Make it float!” (Vysotskaya et al., 2016): co-measuring “floating” and “sinking” materials to balance a vessel in water.

• “Bargaining”: co-measuring different currencies to find the most profitable.

• “Reflections”: co-measuring triangles to hit the target by a laser (reflected with a mirror), or measuring objects’ height by their shadows.

We have chosen “Inks” for 4th-graders in the current study.

Purpose of the Study

Our long-term goal is to study activities that provide students with comprehension of the concept of ratio in the teaching-learning process. We implement the Activity Approach to the practice of school education, in particular the Developmental Instruction Theory (Davydov) (e.g. Dougherty & Slovin, 2004; Giest & Lompscher, 2003; Moxhay, 2008; Zuckerman, 2003). This approach implies reconstruction of the origin of a concept in material actions of students (Davydov, 2008). This is what we strived to do designing the module on paint-making, called “Inks”. We are working within the Educational Design Framework (Van den Akker, 2006) and will focus on the local instruction theory we have devised..

Research Methods

Within the educational design research framework we have formulated our instruction theory. Our module is called “Inks”: it was held 1 lesson a week during one year - 30 hours in total. 56 students (4th grade, 10-11 years old) have undergone our course during two years (one class a year). During these two years classroom discussions were video-taped and students were interviewed to see, what exactly they are relying on when solving a problem and what argumentation do they use. To assess how the students have assimilated the concept of concentration a special test was devised. The results were compared to that of the control group (124 students who had same Math lessons as the experimental group – 5 classes).

“Inks” module

“Inks” module was designed to allow students take control over some actual changes corresponding a ratio. Our course was about making different shades of paint. Students were working in pairs – each in charge of his own parameter – either water, or ink. Inks were measured with “drops” and water – with millilitres. Each paint-receipt was prepared and then tested on a paper blank to see, if it fits the task. Their tasks varied: making the same paint as given, making the given paint lighter or darker in shade. Problem setting evolved: first students had to mix pure ingredients: ink and water, further on they had to deal with a ready-made mixture and ink or water, in the end they even had to mix ready paints only.

See Full Size >

The development of learning situation was meant to scaffold the development of students’ actions from the moment they appear as joint co-measuring of two students till they become one’s mental actions. The “steps” of the “Ink” module are as follows:

• Recipes. Students learn to write down recipes and prepare paints by a recipe. A recipe served as a model – first to bring down “nice” paints, then – to plan paint-mixing beforehand. At this step students also learned the effects of water and ink on the shifts of colour (Fig.02).

See Full Size >

• Further on recipes became an instrument, a model that mediated working over a new problem: how do we keep or change shades of paint? Subsequently there was a wide range of tasks: to prepare more paint of the desired shade (or vice versa – a small portion), to make the given paint darker or lighter. The compound measure – the smallest portion of water and ink – is to be constructed for each paint given. It allows to prepare any amount of paint of the desired shade.

• At this step students operated mixtures rather than separate ingredients: splitting or mixing paints of different or common shade - so that the students would have to study and master compound measures as their own mean to solve problems.

The restrictions that this context poses are as valuable as the opportunities it provides. On the one hand, the context allows to work with parameters separately and to observe the resulting changes of the third parameter. On the other hand, some operations cannot be done (i.e. taking inks or water from paint), and these restrictions are a great source of interesting tasks for students. The context is non-artificial –perhaps, that is why it is easily understood and accepted by the students. In addition, the context does not demand introducing new phenomena (for example density concept first requires to introduce the idea, that vessels can be balanced in water). Students in primary school are familiar with paint-mixing and the task “to make the same shade of blue” is clear enough to start working over the problem.

Findings

Our results show significant differences between the experimental and control group in tasks №1-6, but the tasks № 7, 8 and 9 were done equally good by both groups (see Figure 03 and Table 01 ).

See Full Size >

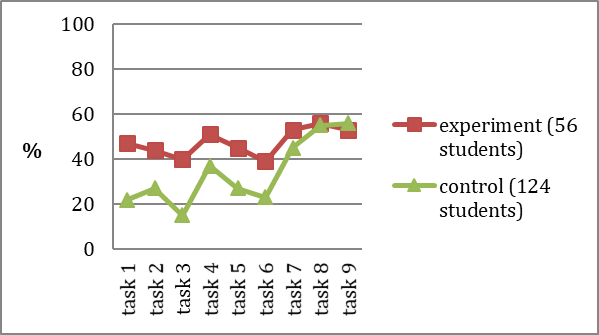
To begin with, the performance of both groups is poor: with a maximum level of about 55 percent of students, who have solved word problems № 8 and 9. That means, that our experiment group, though significantly better, than other children, still experienced difficulties with ratio-problems. 30 hours may seem a significant amount of time, but (1) it was scattered during the whole school year and (2) the module was optional. Unfortunately, students did not take it seriously (which affected attendance rates and home assignments, which they preferred not to do). In the future we hope to integrate the module in the basic Math curriculum – so students will take the assignments seriously.

Now we will discuss the results of different groups of tasks.

The tasks that required constructing one parameter, using the given “recipe” and the value of related parameter (№ 2, 4, 5, 8, 9), ranged in difficulty. The ratio between the values could be simple (1:3 in task № 8) or easy to grasp (task № 9). Task № 9 prompted students to do division as it contained 49 and 28 – and most students remember well, that 49=7*7 (thus they successfully solve the task: 28:4=7, 49:7=7). Both tasks (№ 8 and 9) were done equally good by experiment and control group.

Other tasks (№ 1, 3, 6, 7) required comparing something, made by different “recipes” – in terms of Arithmetic students compared fractions with different numerator and/or denominator. Most often students of the control group used subtraction to solve the problem. This is how they ponder over the third problem (see 5.2): “They both performed equally good. Ira hadn’t solved 5 tasks and Jura also hadn’t solved 5. He simply had more tasks to do. 15 – 10 = 5 and 20 – 15 = 5”. It is interesting though, that if the task is changed, so that the difference in effectiveness becomes more obvious, students do not appeal to subtraction:

Teacher: What if Ira solved 1 task out of 6, and Jura – 5 out of 10…

Student: Then, Jura, of course.

T.: But the difference is also 5 tasks. They both have not solved 5 tasks.

S.: But it is an absolutely different problem!

Most students of the control group were applying the same strategy (using differences instead of ratio) to the problem with making salty water for a fishbowl (task № 6). Perhaps, high performance in the 7^th task is due to the difference: 24 months is equal 16 and a half (8 months) and 18 models is 12 models + 6 (half of 12). Thus students grasp ratio, analyzing differences, and solve the problem correctly. Nevertheless, if the ratio in the task is less obvious, the difference between the experiment and control group becomes significant. These results correlate with findings in the study of Cramer, Post and Currier (1993).

The phrasing of the word problem is also essential. Task № 1 goes:

Kids decided to paint school stadium green, but they had only yellow (y) and blue (b) dyes. Each of them took some jars and mixed them in his own bucket as follows:

Kolya: y y y y b b b b b b

Tolya: y y y b b b b b b

Misha: y b b

Olya: y y b b b

Grisha: y y y b b b b b

Ira: y y y y b b b b b

Jura: y y b b b b

Jura started painting, but his dye was not enough. Does someone else have the same shade of green to continue painting? What is the recipe for Jura’s paint?

Control group was not used to this sort of tasks: the task does not have any numbers, the information is presented as “notches” – each letter stands for one jar of dye. Most students in both groups found only 1 answer, though there are two paints similar to Jura’s recipe.

See Full Size >

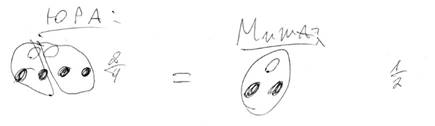
Task № 1 interested us most. This task meant to test, what percent of the students in the control group had accomplished the module successfully. As we have mentioned above, the module was optional and many students did not take it seriously. Indeed, only half of the students have solved the one problem that obviously dealt with course materials. And that means, that only about half of our experiment group had learnt well, what they were taught. Indeed, in other tasks students do not pass the border of 56 % percent, but they also do not go lower, than 39 %.

Thus, we can suggest, that there are two subgroups in both experimental and control classes. There are students in both group, who could not accomplish tasks №7, 8, 9 – those, that were done equally good in both groups, because the ratio there was easy to grasp. Why did the experiment group did not perform better? We suggest that those, who did not study hard or did not take the test seriously, performed the same in both groups. The second subgroup consists of those students, who were successful in the last three tasks. We can suppose that these students are “diligent” ones – and they are present in both groups. But “diligent” students of the control group could not manage other tasks, whereas “diligent” students of the experiment group were relatively efficient. We assume, that it is our instruction that provided them with the concepts (read “mental instruments”) needed to solve the tasks.

Speaking of the subgroup that was not efficient, we would like to say, that in our module they are not merely “left behind”. They have a special role from the beginning: they “play” opponents in class discussions, as they solve some problems according to “common sense” and some solutions they suggest are based on additive thinking. It is vital for all students to experience this collision between “what it seems true” and “what it really is”, between proportional contexts (that need multiplicative thinking) and contexts, where it would be inadequate. We do not hand out ready algorithms and all students can lure to “common sense” or make mistakes throughout the course. It is their work to check others’ solutions, discuss different results, argue, refer to models, coordinate work between pairs and in the end – build their own ways of thinking mediated by the ratio-concept. And even those, who were unsuccessful according to the final test, still differ from those, who failed in the control group. They have the potential to get the ratio-concept, but their future learning, as well as a more profound analysis of our main matter of interest – when and how to learn proportions – will be the subjects of our next researches.

Conclusion

Our results have convinced us, that the instructional strategy we devised managed to provide students with a working ratio-concept.

Some aspects of the module “Inks” are the most essential:

• control over a ratio-parameter

• “compound” measure

• joint actions – “co-measuring”

• internalisation to mental acts.

The central idea of our module was to deliver students the sense of what they do. As they could observe the shades of paint and compare them with the result needed, the control over the whole process was in their hands. The teacher was no longer the only one who knows, whether they were right or wrong. Thus, she could step aside and provide students with tasks and materials only, but refrain from making conclusions, suggesting solutions (to prompt students she suggested wrong solutions though) and handing out marks. Indeed, students’ actions regained some purpose and meaning as compared to that of their peers. Usually it is the material itself that stimulates students’ actions: the texts urge students to wright down some formulas, formulas induce solutions, an answer is written while a student scarcely can explain, why and how it was done. As they aimed to achieve some perceptible result (the exact shade of colour), they had to revise constantly their solutions. Their discussions, their resistance to teacher’s traps showed, that they are aware of what and why they are doing.

Students assimilated the instrument that we have constructed to mediate students’ work – the compound measure – and they actually relied on it while solving problems. They transferred this mean to other ratio-based contexts. “Hey, it’s like paints!” – they said, when dealing with trade-context.

Co-measuring with a compound measure indeed scaffolds ratio-concept formation. The discussions and working with materials that take place during problem-solving collapse after some time, but unfold whenever the problem situation evolves.

Moreover, joint co-measuring was rewarding in terms of communication skills – students learned to work in pairs. As the assignment could not be done individually, it was natural for both students in pair to work and discuss the matter. The teacher didn’t have to stimulate this process artificially.

Thus, we conclude, that teaching ratios in primary school (4th grade) is feasible. The context we use provides meaningfulness, and the compound measure is a powerful instrument that mediates students’ activity – from joint co-measuring to an individual mental act.

References

1. Almuntasheri, S., Gillies, R. M., & Wright, T. (2016). The Effectiveness of a Guided Inquiry-Based, Teachers' Professional Development Programme on Saudi Students' Understanding of Density. Science Education International, 27(1), 16-39.
2. Ben-Chaim, D., Keret, Y., & Ilany, B. S. (2012). Ratio and proportion. Springer Science & Business Media.
3. Braithwaite, D. W., & Siegler, R. S. (2018). Developmental changes in the whole number bias. Developmental science, 21(2), e12541.
4. Chen, Y. C., Lin, J. L., & Chen, Y. T. (2014). Teaching scientific core ideas through immersing students in argument: using density as an example. Science Activities: Classroom Projects and Curriculum Ideas, 51(3), 78-88.
5. Cramer, K., Post, T., & Currier, S. (1993). Learning and Teaching Ratio and Proportion: Research Implications. In D. Owens (Ed.), Research Ideas For the Classroom (pp. 159-178). NY: Macmillan Publishing Company.
6. Çepni, S., & Şahin, Ç. (2012). Effect of different teaching methods and techniques embedded in the 5E instructional model on students' learning about buoyancy force. Eurasian Journal of Physics and Chemistry Education, 4(2).
7. Davydov, V.V. (2008/1986). Problems of developmental instruction: a theoretical and experimental psychological study. Nova Science Publishers (Original published in Russian in 1986)
8. Dole, S., Clarke, D., Wright, T., & Hilton, G. (2012, July). Students’ proportional reasoning in mathematics and science. In Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 195-202). National Taiwan Normal University.
9. Dougherty, B., Slovin, H. (2004). Generalized diagrams as a tool for young children's problem solving. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 2004, Vol. 2, pp.295-302. PME: Capetown, South Africa.
10. Giest, H., Lompscher, J. (2003). Formation of learning activity and theoretical thinking in science teaching. Vygotsky's educational theory in cultural context. Ed. by A. Kozulin et al. Cambridge University Press., p.267-288
11. Hecht, S.A., Vagi, K.J., & Torgesen, J.K. (2007). Fraction skills and proportional reasoning. Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. By D.B. Berch, & M.M.M. Mazzocco (Eds.). Baltimore, MD: Paul H. Brookes Publishing Co. pp. 121-132.
12. Hilton, A., Hilton, G., Dole, S., & Goos, M. (2013). Development and application of a two-tier diagnostic instrument to assess middle-years students’ proportional reasoning. Mathematics Education Research Journal, 25(4), 523-545.
13. Jansen, B. R., & van der Maas, H. L. (2002). The development of children's rule use on the balance scale task. Journal of Experimental Child Psychology, 81(4), 383-416.
14. Kloosterman, P. (2010) Mathematics Skills of 17-Year-Olds in the United States: 1978 to 2004. Journal for Research in Mathematics Education, 41, 20-51.
15. Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. Second handbook of research on mathematics teaching and learning, 1, 629-667.
16. Leontiev, A.N. (1981). The problem of activity in psychology. In J.V. Wertsch (Ed.), The concept of activity in Soviet psychology (pp.37-71). Armonk, NY: Sharpe. (Original published in Russian in 1972).
17. Mahajan, S. (2005). Observations on teaching first-year physics. arXiv preprint physics/0512158.
18. Moli, L., Delserieys, A. P., Impedovo, M. A., & Castera, J. (2017). Learning density in Vanuatu high school with computer simulation: Influence of different levels of guidance. Education and Information Technologies, 22(4), 1947-1964.
19. Moxhay, P. (2008). Assessing the scientific concept number in primary school children. Paper presented at ISCAR 2008, San Diego, USA, September 8-13, 2008.
20. Nunes, T., Desli, D., & Bell, D. (2003). The development of children's understanding of intensive quantities. International Journal of Educational Research, 39(7), 651-675.
21. Ölmez, İ. B. (2016). Two Distinct Perspectives on Ratios: Additive and Multiplicative Relationships between Quantities. İlköğretim Online, 15(1).
22. Siegler, R.S., Chen, Z. (2008). Differentiation and integration: Guiding principles for analyzing cognitive change. Developmental Science, 11, 433-448.
23. Smith, J., & Thompson, P. W. (2007). Quantitative reasoning and the development of algebraic reasoning. In J. J. Kaput, D. W. Carraher & M. L. Blanton (Eds.), Algebra in the early grades (pp. 95-132). New York: Erlbaum
24. Stott, A., & Hattingh, A. (2015). Conceptual tutoring software for promoting deep learning: A case study. Journal of Educational Technology & Society, 18(2), 179.
25. Van den Akker, J., Gravemeijer, K., et al. (Eds.). (2006). Educational design research. Routledge.
26. Vygotsky, L. S. (1962). Thought and language (1934). Trans. Eugenia Hanfmann and Gertrude Vakar. Cambridge, MA: MIT P.
27. Vysotskaya, E., Rekhtman, I., Lobanova, A., & Yanishevskaya, M. (2014). From proportions to fractions. In EAPRIL Conference Proceedings 2014, 42-53.
28. Vysotskaya, E., Lobanova, A., Rekhtman, I., & Yanishevskaya, M. (2016). Make it float! Teaching the concept of ratio through computer simulation. EAPRIL 2016, 297.
29. Zuckerman, G.A. (2003). The learning activity in the first years of schooling: the developmental path towards reflection. Vygotsky's Educational Theory in Cultural Context. Ed. by A. Kozulin et al. Cambridge University Press., p. 177-199.