Interlingua-Based Numeral Translation In Web-Application With Knowledge-Testing

Interlingua-based translation

The Interlingua is an intermediate representation of translating text (Dorr, Hovy & Levin, 2004; Lampert, 2004; Lee & Seneff, 2005). There are two steps in the Interlingua-based translation: 1) converting the source language text into the Interlingua; 2) converting the Interlingua into the target language text. The translation is easy-extending. To add new language in multi-lingual translating system you need to develop the language-Interlingua converting algorithms.

We use such Interlingua-based translation to process numerals in the text. We describe the Interlingua representation with the formal grammar.

G. Hardegree grammars

Gary Hardegree proposed grammars (Hardegree, 1999) for representation of the numeral structure and number transformation into English numerals. The grammars can be intended only for numeral building and used only in English. The grammars also describe the rules of building only for integer parts of numerals, but don’t consider numeral case inflection as there is no case grammatical category in English.

Three-level generalized numeral model

To describe a generalized numeral structure for the Interlingua representation by the formal grammar, we use the following terms.

Number terms are:

The numeral terms are:

Example 1. In this terms, the number

1 000 400 973 = Z ₁ Z ₀ Z ₀ Z ₀ Z ₄ Z ₀ Z ₀ Z₉ Z ₇ Z ₃

presents as:

P ₊ C ₁ M ₃ C ₄ D ₂ M ₁ C ₉ D ₂ C ₇ D ₁ C ₃ M ₀ EB . □

The terms are necessary for model generalization and language independence.

We analyze the natural languages numeral building rules and develop a three-level generalized numeral model (or model ) as the Interlingua. It consists of the following levels.

Level 1 renders numeral sign and integer and fractional parts. Part delimiters are patch words « comma », « point ».

Level 2 renders three-digit ingredients (triads). Each part is divided into three-digit ingredients beginning with integer and fractional parts separating char. Three-digit ingredients part delimiters are patch words « thousand », « million », etc.

Level 3 renders three-digit ingredients items. Part delimiters are patch words « tens », « hundreds ».

Example 2. Figure 01 illustrates the three-level generalized numeral model structure by the example of number 34 567.89. □

See Full Size >

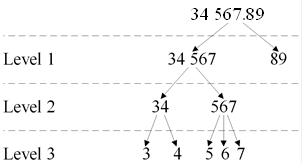
The model grammar rules are shown below.

Level 1:

K = P + N ₁ + E + {| N ₂} + B

P = P _-| P ₊| P ₀

Level 2:

N ₁ = С ₀| N ₁₀| N ₁₁| N ₁₂|...| N _{1 i} |...

N ₂ = ({ T ₁| C ₀} + N ₂)| T ₁| C ₀

N ₁₀ = T + M ₀

N ₁₁ = T + M ₁ + {| N ₁₀}

N ₁₂ = T + M ₂ + {| N ₁₀| N ₁₁}

...

N _{1 i} = T + M _i + {| N ₁₁| N ₁₂|...| N _{1( i –1)}}

...

Level 3:

T = T ₁| T ₂| T ₃

T ₁ = C ₁| C ₂| C ₃| C ₄| C ₅| C ₆| C ₇| C ₈| C ₉

T ₂ = T ₁ + D ₁+ {| T ₁}

T ₃ = T ₁ + D ₂ + {| T ₁| T ₂}

The model is a generalized numeral structure using in programming of number-into-numeral, numeral-into-number, and translating algorithms.

Converting algorithms

We use Markov normal algorithms (Markov, 1954) to implement converting algorithms.

We add new operations and symbols to simplify the algorithm normal scheme:

→ + $$ – to add symbol $$ at the end of the word;

→ $$+ – to add symbol $$ at the beginning of the word;

[ Z ₀] _k – k zeros sequence;

_ (underlining) – space symbol.

In this section we present some basic converting algorithms.

Number-into-model integer part converting algorithm replaces digits by numeral terms.

1) Z _k ${\gamma }_1^j$ → ${\gamma }_2^j$ C _k M _j ; j = 0, 1, 2, …; k = 1, 2, …, 9

2) Z _k ${\gamma }_2^j$ → ${\gamma }_3^j$ C _k D ₁; j = 0, 1, 2, …; k = 1, 2, …, 9

3) Z _k ${\gamma }_3^j$ → ${\gamma }_1^{j+1}$ C _k D ₂ ; j = 0, 1, 2, …; k = 1, 2, …, 9

4) Z ₀ Z ₀ Z ₀ ${\gamma }_1^j$ → ${\gamma }_1^{j+1}$; j = 0, 1, 2, …

5) Z ₀ ${\gamma }_1^j$ → ${\gamma }_2^j$ M _j ; j = 0, 1, 2, …

6) Z ₀ ${\gamma }_2^j$ → ${\gamma }_3^j$; j = 0, 1, 2, …

7) Z ₀ ${\gamma }_3^j$ → ${\gamma }_3^j$; j = 0, 1, 2, …

8) ${\gamma }_2^0$ M ₀ E → P ₀ C ₀ EB •

9) S _- ${\gamma }_i^j$ C _k → P _- C _k •; i = 1, 2, 3; j = 0, 1, 2, …; k = 0, 2, …, 9

10) ${\gamma }_i^j$ C _k → P ₊ C _k •; i = 1, 2, 3; j = 0, 1, 2, …; k = 0, 2, …, 9

11) J → ${\gamma }_1^0$ E

12)→ + ${\gamma }_1^0$ EB

An index symbol marks processed symbol in the number.

Model-into-number integer part converting algorithm transforms a numeral integer part into a number integer part.

1) M _j ${\gamma }_i^L$→ ${\gamma }_i^j$ ${\left[Z0\right]}_{\mathrm{4}–i+\mathrm{3}\left(j–L–\mathrm{1}\right)}$; i = 1, 2, 3;

L = 0, 1, 2, …; j = L +1, L +2, …

2) M _j ${\gamma }_i^j$ → ${\gamma }_i^j$; j = 0, 1, 2, …

3) C _k ${\gamma }_1^j$→ ${\gamma }_2^j$ Z _k ; j = 0, 1, 2, …; k = 1, 2, …, 9

4) C _k D ₁ ${\gamma }_i^j$ → ${\gamma }_3^j$ Z _k [ Z ₀]_{2– i} ; i = 1, 2; j = 0, 1, 2, …; k = 1, 2, …, 9

5) C _k D ₂ ${\gamma }_i^j$ → ${\gamma }_1^{j+1}$ Z _k [ Z ₀]_{3– i} ; i = 1, 2, 3; j = 0, 1, 2, …; k = 1, 2, …, 9

6) P ₊ ${\gamma }_i^j$ Z _k → Z _k •; i = 1, 2, 3; j = 0, 1, 2, …; k = 1, 2, …, 9

7) P _- ${\gamma }_i^j$ Z _k → S _- Z _k •; i = 1, 2, 3; j = 0, 1, 2, …; k = 1, 2, …, 9

8) P ₊ ${\gamma }_i^j$ Z ₀ → Z ₁ Z ₀ •; i = 2, 3; j = 0, 1, 2, …

9) P _- ${\gamma }_i^j$ Z ₀ → S _- Z ₁ Z ₀ •; i = 2, 3; j = 0, 1, 2, …

10) P ₀ C ₀ EB → Z ₀ •

11) EB → ${\gamma }_1^0$

12) E → ${\gamma }_1^0$ J

The algorithm also use the index symbol .

The algorithm using the model checks numeral for errors as well. 6-9 replacements execution is a correct algorithm ending. None of the replacements execution means that a numeral contains an error.

Number-into-model fractional part converting algorithm is shown below.

1) Z _k → C _k ; k = 0, 1, …, 9

2) → B •

3) E → E

In this algorithm the index symbol is a Greek alphabet letter.

Model-into-number fractional part converting algorithm replaces numeral terms while all terms will processed.

1) C _k → Z _k ; k = 0, 1, …, 9

2) C _k B → Z _k •; k = 0, 1, …, 9

3) EB → EB •

4) E → E

Numeral translation order

The model terms have general nature. In each language, they have unique types. For example, in the Russian language C ₀ = « ноль », C ₁ = « один », etc.

In some languages, numerals are formed by the rules that are different from the model rules. In this case, numeral is converted by algorithms. Two algorithms are necessary:

1) numeral-into-model converting algorithm transforming a numeral in the model representation into a numeral of the target language;

2) model-into-numeral converting algorithm transforming a numeral of the source language into a model numeral.

These algorithms carry out the opposite actions.

Number-into-numeral converting includes four steps:

1) to execute the number-into-model integer part converting algorithm;

2) to execute the number-into-model fractional part converting algorithm;

3) to execute the model-into-numeral converting algorithm if it exists;

4) to replace model terms by language symbols in required case.

Numeral-into-number converting consists of the following steps:

1) to replace language symbols by model terms;

2) to execute the numeral-into-model converting algorithm if it exists;

3) to execute the model-into-number fractional part converting algorithm;

4) to execute the model-into-number integer part converting algorithm.

Using the model, we can translate numerals. Translation of a numeral from the L1-language into the L2-language includes four steps:

1) to replace the L1-language symbols by the model terms;

2) to execute numeral-into-model converting algorithm if it exists for the L1-language;

3) to execute model-into-numeral converting algorithm if it exists for the L2-language;

4) to replace the model terms by the L2-language symbols in required case.

All algorithms in this paper are implemented in web-application.

Web-application with knowledge-testing function

In 2012 we have developed (with Dmitriy Tsybulko) a web-application for processing of the natural language cardinal numerals. The web-application is available to users of the Internet at http://prutzkow.com/en-us/numbers/ (the English-language version) or http://prutzkow.com/ru-ru/numbers/ (the Russian-language version).

The web-application has the following functions:

1) translation of numerals of Russian, English, German, Spanish and Finnish languages in any direction (because of the Interlingua-based technique);

2) number-into-numeral and numeral-into-number converting;

3) declination of numerals of the Russian language;

4) numerals converting and translating knowledge testing.

The web-application was integrated in the toolkit of the My-Polyglot.com expert network for translators.

User request statistics

Each request to the web-application is recorded in the log. The log uses for web-application debugging and analyzing of request statistics. A record of the log includes the following request data:

There are more than 200,000 records in the log in this moment.

We analyzed the log and present numeral translating direction statistics in Table 01 .

In Table 01 , each cell contains three values. The upper value corresponds to 2014, the middle value corresponds to 2015, and the lower value corresponds to 2016.

The most of users of the web-application reside in the US and Russia (Table 02 ). The trend has not changed for the last three years. Users of the web-application live in more than 100 countries on all permanently inhabited continents. The data for Table 02 includes all requests, even erroneous.