Abstract
In figure skating, the athletes reach remarkable performances at younger ages than in the last twenty years, when senior’s skaters were the only ones who managed to do triple rotation jumps. In the present, rotation jumps are being learned starting from 12 or 13 years old. By increasing efficiency of the learning process it shorten significantly the length of time in which the athletes passes the threshold from one at two, three or four rotations, performance that requires both, special motoric abilities and a careful guidance from the coach. The initial premise from which our study started was the importance of height jumping that is considered being essential in carrying out thedifficulty technical elements in figure skating. The purpose of our study is to highlight the differences between parameters at simple vertical jumps and those with one or two rotation at figure skating. For this study we used the OptoJump device, we have identified and measured the jumping determinant parameters in skating, namely: jumping heights, the power generated at the jumping point, the time spent in air and the time spent on the ground, to a lot of 7 junior figure skaters. Doing the statistical analysis of these items, we showed the importance of the jumping height in the preparation of the figure skaters performance, the differences between simple vertical jumps and those with one or two rotation, and we compared these results with the notes obtained by sportsmen at the contests throughout competitive season.
Keywords: Detentfigure skatingvertical jumpsdeterminant parameters
Introduction
Jumps are a set of codified gestures whose aim is to traverse a certain distance, using the longest
or highest trajectory (King, 2004a). They can also represent athletic events of a highly spectacular degree,
which overtime have known several changes in regards to the technique or the procedure used to achieve
performance. In athletics, jumps represent an auto projection of the body in space, in one or several
jumps. In essence, the aim is having the longest horizontal trajectory in the air for a length jump, and
vertically for a height jump. To achieve this all internal and external forces that engage need to correlate.
(Polensky, Kaufman, Calahan, Aleshinsky, Chao, 1990). The specificity of jumps involved in figure
skating is the aspect of the trajectory and the rotation or rotations occurring in the air, around own axis.
(King, 2000). The more rotations are carried out in the air during jumps, the more spectacular and
valuable they are in terms of Code of Points. This involves the skater’s detachment in the air and him
executing fast rotations, the jumps being finalized in landing. (King, 2000).
Theoretical Framework
There are certain limitative factors that converge to successfully finalising a jump with several
rotations in the air (Aleshinsky, Smith, Jansen, and Ramirez, 1988). The main motoric actions involved in
figure skating jumps are:
•Auto propelling in space – creating oriented actions on ice, in order to realise technical actions
specific to each task. (King, Smith, Casey, 2002).
•Using the reaction of the surface of the ice to the own action of the skate’s blade, transferring
them with minimal loss, the importance of aligning the segments when beating and taking off, as well as the one of the segmentary fixation (King, Arnold, and Smith, 1994).
Ensuring the balance of the body on the flight trajectory (King, 2005).
Rationally using the real rotations during flight and due to the force and direction of detachment.
The compensation or accentuation of these sorts of rotations in order to keep the balance on
trajectory, which is achieved using segmentary compensatory rotations, done by upper and lower
limbs (King, Smith Higginson, Muncasy, Scheirman, 2004b).
•Achieving a segmentary controlled displacement in the flight phase, consistent with the
mechanical characteristics of the trajectory of flight. (Aleshinsky, 1986).
•Optimising and securing the landing according to the statutory requirements of the jump. (Albert,
and Miller, 1996).
Research Design
The Study Objectives
The main objective of our study was to identify the determining parameters of rotational jumps in figure skating done on land. The secondary objectives were:
Measuring the determining parameters of rotational figure skating jumps.
Conducting the comparative/descriptive statistical analysis
Highlighting the conditions of carrying out of the rotational jumps.
The Research Data
Our study has been carried out during the competition season Oct 2015 – May 2016. Measuring
the determinant parameters of rotational jumps has been performed at the end of the season, on Oct 24th
2016, outside the skating rink, with 7 ice skaters that took part in national and international competitions
for beginners. This age category represents a turning point in an ice skater’s career and links the
competitions for children and the ones for juniors. Subjects were aged 10-13, their height was 136-156
cm, their weight average was 35,3±6 Kg, and their shoe size was 35,14±2 cm.
The Research Methodology
Testing has been performed with Opto Jump (fig.1), a device used to measure and evaluate some
parameters of the detent, like: explosively, elasticity, reaction time, time spent by the sportsman in the air
and on the soil.

In our research we used
seconds, as many consecutive straight vertical jumps, jumps involving one or more rotations. All
sportsmen have visualized, on the device’s display, their results in real time, and also heard the coach’s
indications, which corroborated with the image given by the device. The software of this device has
delivered data concerning the time spent on the soil, TS, time spent in the air during jump, TA, the height
of the jump, HJ, and the total jump power, JP, during vertical straight jumps, S1, jumps with one rotation
(360°), S2, and two rotations in the air (720°), S3. During the competition season sportsmen have each
had observation charts based on the results of arbitration charts from the contest, and the final test has
been carried out during a training outside the rink to highlight differences between straight vertical jumps
with one and two rotations.
Results. Analysis and Interpretation
Final results for time on the soil
one rotation (
We have
(360°), and
the straight vertical jump,
spent in the air for the two-rotation jump (720°).
Results regarding contact time on soil
In regards to the time spent on soil, Opto-jump has highlighted the amount of time the sportsman spent
on the ground between landing and detachment to perform the next jump, as seen in table no. 1 and graph
in fig. no. 2.
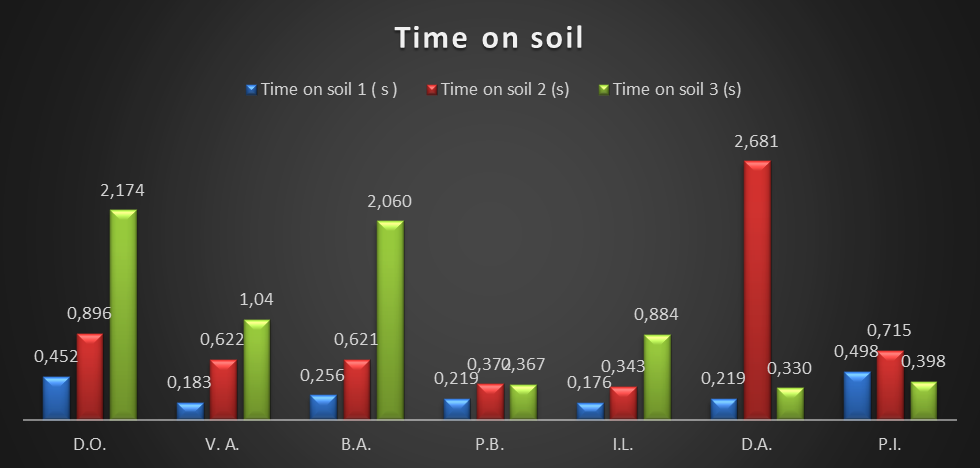
Time on soil is different depending on the difficulty of the jump that the sportsman has to perform
and the executant’s level of training. We can see from the previous graph that the sportsman needs more
preparation time for harder jumps (in our case one-rotation and two-rotation jumps) and their frequency
within 15 seconds decreases from 15-20 simple jumps, to 2-4 two-rotation jumps. The average time spent
on soil for first jump, TS1, was 0,286 seconds, second, TS2, was 0,893 seconds, and for the third jump,
TS3, was 1,036 seconds. The difference between the contact time on soil for the straight vertical jump
and the one-rotation jump was 0,607 seconds, and this significant difference is due to the 6th contestant,
who needed a preparation time of over 2 seconds for the one-rotation jump following the straight vertical
jump. The difference between the average of the first jump, TS1 and the third, TS3 is 0,75 seconds, and
between the second, TS2 and the third, TS3 is 0,143 seconds. Therefore, the contact time on soil, the
preparation time for the jump, considerably increases when the rotation is present, and there is no
significant difference between the preparation time for the two-rotation jump compared to the one for the
one-rotation jump. Different results only occured for the first sportsman, for whom TS3 was three times
TS1, sportsman no. 3 with TS3 almost 10 times TS1, and sportsmen no. 6 and 7 with TS3 less than TS1.
Results regarding time spent in the air
In the following graph we compared times spent in the air for each jump the sportsmen have performed:
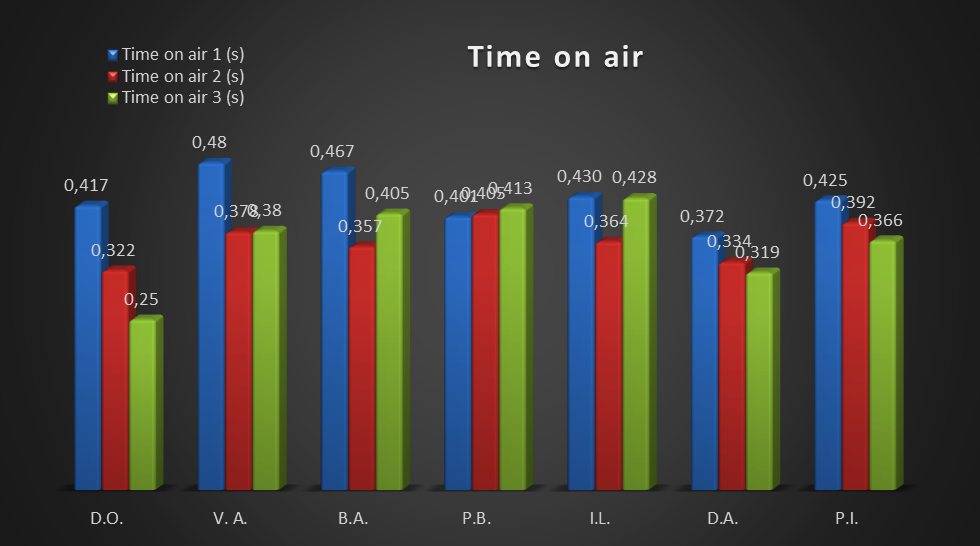
As it can be seen the time spent in the air for the vertical jump TA1, (in blue) is on average 0,063
sec longer than for one-rotation jumps, TA2, (in red). The difference between the amount of time spent in
the air during straight vertical jumps, TA1 and the two-rotation jumps, TA3 is 0,061 sec. The difference
between the amount of time spent in the air during the one-rotation jumps, TA2, and two-rotation jumps,
TA3, (in green) is just 0,001 sec. According to these results, the time spent in the air for a two-rotation
jump is approximately equal to the time for a one-rotation jump and less than for the straight vertical
jump, with one exception when time on air 1 is less than time on air 2 and 3. The time average for the first
jump is 0,427 seconds, and for the one- and two-rotation jumps times are approximately equal, 0,365 and
0,366 seconds.
Results regarding the height of the jump
The straight vertical jumps have been analysed acording to their validity, as in invalid jumps were
the ones when the sportsman has gone over the surface of the sensors and they were eliminated. The
results recorded for jump height are represented in table no.2 and graph in fig.
jump height,
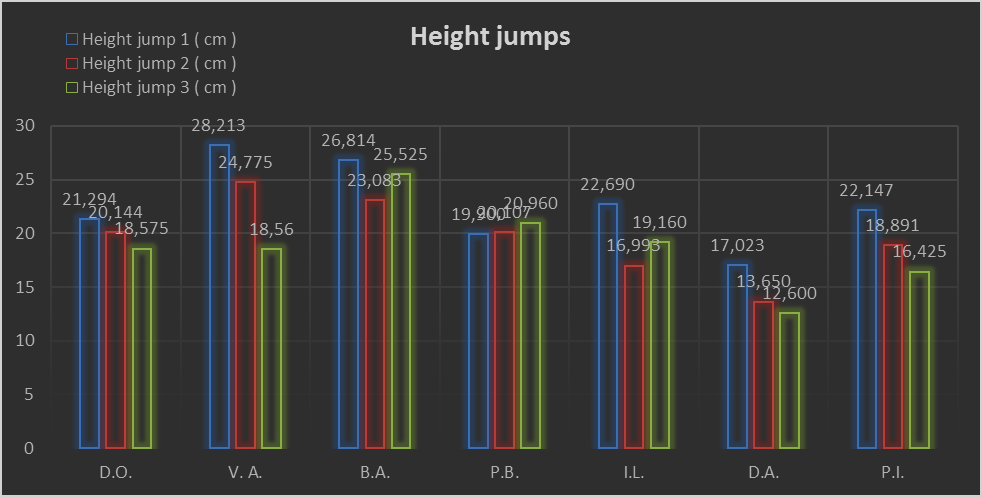
In our research we measured the height of jumps in cm, we calculated and used the average of
statistical data. From table
jumps, HJ1 is 2,92 cm greater than the average height of one-rotation jumps, HJ2, and 3,754 cm greater
than the average of jumps 3, HJ3. The aveerage of one-rotation jumps, HJ2 is 0,834 cm greater than the
average height of two-rotation jumps, HJ3, so a minimal difference. Just sportsman 4, P.B., had the height
of the second and third jump 0,207cm, and 1,06 cm higher than the first jump.
Results regarding the power of jump
In the present research power is represented by the force with which the sportsman pushes the
ground in orider to propel himself in the air. As for the time spent in the air, power is strongly correlated
with the height of the jump, therefore the results are similar to the ones regarding the height of the jump
and the ones regarding time spent in the air. We have
one-rotation jump (360°), and
and graph in fig. no.5.
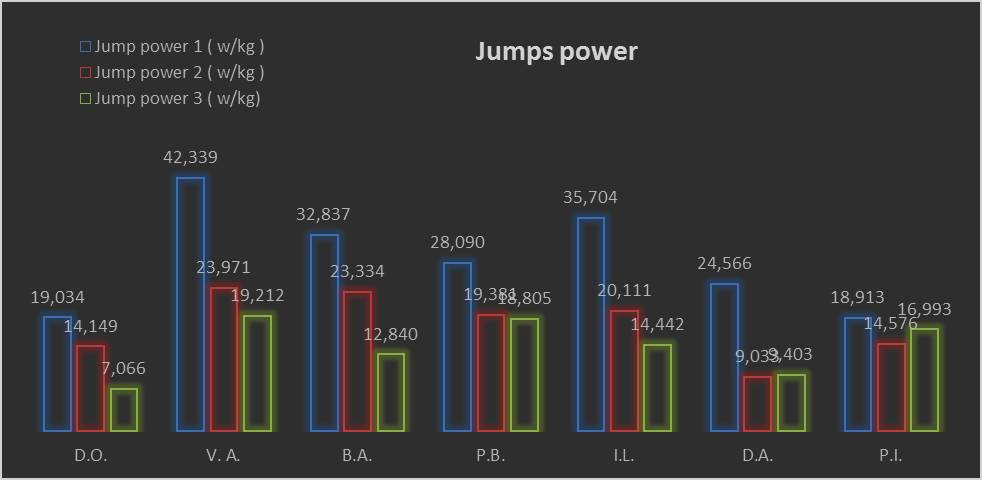
In regards to the power of jumps performed, for all sportsmen involved in the measurements, the
power of the first jump, the straight vertical one, JP1, is greater than the power of the second jump, JP2,
and the third, JP3. Only one sportsman has developed greater power for the second jump, JP2, omparing
to the third, JP3, by 2,417 w/kg. The average power for straight vertical jumps, JP1, is 10,989 w/kg
greater than the one for one-rotation jumps, JP2, and 14,674 w/kg greater than the average power for two-rotation jumps, JP3. The average power of one-rotation jumps, JP2, is 3,685 greater than the average for
two-rotation jumps JP3.
Conclusion
By identifying the determinant parameters of the rotational jumps involved in figure skating, the
main objective of our study has been achieved. In our view these are: the time spent on the ground,
meaning the preparation time (TS), the time spent in the air (TA), the height of the jumps (HJ), and the
power of the jumps (JP).
Through measuring these parameters and the statistical analysis performed, we also achieved two
of our secondary objectives of our study. Hence, through the graphical analysis we reached the
conclusions that the time spent in the air (TA), the height (HJ) and power (JP), the statistical data for the
one- and two-rotation jumps is less than the statistical data for the straight vertical jumps.
As for the time spent on soil, with one exception, sportsmen spent a greater amount of time on the
ground for the third jump, TS3, than for the second TS2, - by 0,143 seconds, - and 0,75 seconds less than
for the first jump, TS1. So it takes a greater amount of preparation time on the ground for the one-rotation
jump, and for the two-rotation jump.
As for the time spent in the air, we expected that to be a greater amount of time in which regards
the one- and two-rotation jump. Our research proved that the greatest time is required for the straight
vertical jump, TA1, which is 0,062 seconds greater than the one for the one-rotation jump, TA2, and
0,061 seconds greater than the time spent in the air for the two-rotation jump, TA3.
Statistical data for the height of the jump show that the first jump, HJ1, with no rotations, is the
highest jump, 2,920 cm higher than the one-rotation HJ2, and 3,754 cm higher than the two-rotation
jump, HJ3. The one-rotation jump HJ2 is 0,834 higher than the two-rotation jump HJ3.
Also, the statistical data for the power of the jump show that the power of the first jump, JP1, is
10,990 w/kg greater than the power of the one-rotation jump, JP2, and 14,675 w/kg greater than the two-
rotation jump, JP3. The power of the one-rotation jump, JP2, is 3,685 w/kg greater than the two-rotation
jump, JP3.
As far as the determinant parameters of the jumps involved in figure skating (outside the ice rink)
are concerned, as measured with Opto-jump, analysing the results has shown that the factors considered
to be limitative traditionally speaking were not to be applied for 6 out of 7 sportsmen. The height of a
jump is not limitative criteria for performing multiple-rotation jumps, that being equal or grater for the
straight vertical jump, which is considered a low-difficulty jump, compared to the jumps involving
rotations in the air which are specific to ice skating.
After centralising the data from arbitration charts from the „Santa Claus Cup” contest in Budapest
and comparing that to the indicators for height and power of jumps measured during our research, we
reached the conclusion there is no direct link between the score in the contest and the height or power of the jumps.
Acknowledgements
The professional Opto Jump device, was acquired through the structural funds project: „RTD Institute: High-tech Products for Sustainable Development” (ID123, SMIS 2637, ctr. No. 11/2009).
References
- Albert, W.J., and Miller, D.I. (1996). Take-off characteristics of single and double axel figure skating jumps. Journal Appl. Biomech. 12: 72-87.
- Aleshinsky, S.Y. (1986). What biomechanics can do for figure skating: Part II. Skating 63(10): 11-15
- Aleshinsky, S.Y., Smith, S.L., Jansen, L.B., and Ramirez, F. (1988). Comparison of biomechanical parameters demonstrated by Brian Boitono in the triple and double axel jumps. In: Proceedings of the 12th Annual Meeting of the American Society of Biomechanics (p. 201). Urbana, IL: University of Illinois.
- King, D.L., Arnold, A.S., and Smith, S.L. (1994). A kinematic comparison of single, double, and triple axels. J. Appl. Biomech. 10: 51-60.
- King, D.L. (2000) Jumping in Figure Skating, in Biomechanics in Sport: Performance Enhancement and Injury Prevention (ed V. M. Zatsiorsky), Blackwell Science Ltd, Oxford, UK.
- King, D.L., Smith, S., and Casey, K. (2002). How’d they do that toe-loop? Part I. Skating 79(3): 62-63, 76.
- King, D.L. (2004a). Biomechanics. In: M.A. Bradley and D. Miller (Eds.), Coach’s Guide to Figure Skating Sports Sciences and Medicine (2nd ed.). Rochester, MN: Professional Skaters Association.
- King, D.L., Smith S.L., Higginson, B.K., Muncasy, B., and Scheirman, G.L. (2004b). Characteristics of triple and quadruple figure skating jumps performed during the Salt Lake City 2002 Winter Olympics. Sport Biomechanics. 3: 109-123.
- King, D.L. "Performing Triple and Quadruple Figure Skating Jumps, (2005). Implications for Training" Can. J. Appl. Physiol. 30(6): 743-753. Canadian Society for Exercise Physiology.
- Podolsky, A., Kaufman, K.R., Calahan, T.D., Aleshinsky, S.Y., and Chao, E.Y.S. (1990). The relationship of strength and jump height in figure skaters. Am. J. Sports. Med. 18: 400-405.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
25 May 2017
Article Doi
eBook ISBN
978-1-80296-022-8
Publisher
Future Academy
Volume
23
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-2032
Subjects
Educational strategies, educational policy, organization of education, management of education, teacher, teacher training
Cite this article as:
Gugu-Gramnatopol, C., Ionescu, A., Ochiotan, Ș., & Dăncescu, D. (2017). Determinants Parameters Of Figure Skating Jump. In E. Soare, & C. Langa (Eds.), Education Facing Contemporary World Issues, vol 23. European Proceedings of Social and Behavioural Sciences (pp. 1748-1755). Future Academy. https://doi.org/10.15405/epsbs.2017.05.02.214

