Multidimensional Statistical Analysis of Life Satisfaction of Older People

Abstract

The paper is devoted to a study of dependences between the life satisfaction and the social conditions of older people presented in their main scopes of life. The life satisfaction is one of the components of subjective welfare that in value judgment is interpreted as a thought-and-sense character. The life satisfaction allows estimating the influence of different life scopes of older people and outlining the priority routes of continuous welfare. It is shown that the life satisfaction of older people is ascertained using the specific questionnaire developed for the sociological inquiry. To make older people prosperous it should be known what factors promote well-being and how to provide these factors. Monitoring performs the function of collecting data about a state of the object being evaluated for further analysis. Estimation of own older person’s life in its various forms, expresses significant levels of subjective well-being, revealing the superordinate connection through the content of emotional and evaluative bases, giving multidirectional nature of the subject’s activity, which may be taken into account only at opinion poll.The paper presents the design of the three-factor space model of the nine parameters for the life satisfaction based on the methods of mathematical statistics. Within this three-factor space model, the qualitative differentiation of older people of the Tomsk region was carried out using the seven-cluster model of 400 respondents.

Keywords: Older peoplelife satisfactionwelfaremultidimensional statistical analysis (factorclusterANOVA)

Introduction

Welfare is reflected in the subjective assessment of the life satisfaction. This assessment is the integrated assessment of the available life conditions, welfare including wages, employment, material wealth, living facilities, the quality of interpersonal dealings, participation in social activity, etc. The assessment of the subjective welfare comprises the human involvement into the certain life spheres, the degree of satisfaction of what he/she has and his/her attitude to it. Being the integral parameter, the life satisfaction reflects the assessment of the external life scope. Therefore, the life satisfaction means the subjective assessment of the quality of one or another object, life conditions and activity, life as a whole, relationships between people, and people themselves including satisfaction of themselves.

This concept of the life satisfaction is widely used but is indefinite. So, in order to identify the degree of satisfaction, it is necessary to specify a sense context to the object to be assessed in which the degree of satisfaction will be measured relative to the objects to be assessed. This assessment depends on what is assessed and taken into account by the respondent. It is also necessary to account for the interaction between the welfare components.

The investigation of the satisfaction aspects implies the development of the assessing methodology allowing to obtain the imagination of the certain structural components and factors that influence the degree of satisfaction. The parameters that record the life satisfaction of older people is identified by the optimality of the living space organization that allows people to be healthy, active, capable of coping the difficulties and achieving their goals, and have a support from other people.

The problem of measuring satisfaction factors and welfare is one of the main parameter in the system of assessing the continuous welfare of older people (Ivankina et al., 2015).

A combination of statistical data and the analysis of life satisfaction that can be used to process measuring data are identified by the type of measuring scale. A sociological inquiry provides three types of measuring scales, namely: nominal (sex, residence); ordinal (estimation of satisfaction); interval (age, income). The problem of sociological measurements is the use of the quantitative interval scale along with the qualitative (nominal and ordinal) so as to solve the majority of problems of empirical sociology. This is because this scale that is used to measure such important characteristics as age, wages, etc. However, in sociological problems, the interpretation of results of the variational series is often more adequate and leads to the approximation of the interval scale of respondent’s characteristics to the ordinal or even nominal scales. Thus, the processing sociological data can be carried out using such methods of mathematical statistics as correlation, factor, dispersion, and cluster analyses.

Problem statement and research methodology

Statistical data are obtained from the sociological inquiry on concerning the problem of welfare of older people of the Tomsk region. These data are presented in Table 1 .

General distribution of respondents on life satisfaction is shown in Table 2 .

Presented in the Table 2 data allow to identify differences numerically, for example, for 5 levels of 9 life satisfaction kinds depending on other indications, but don’t allow to assess the statistical significance of differences. To solve this problem, this research applied the methods of mathematical statistics: correlation, factor, analysis of variance (ANOVA) and cluster analysis (Soshnikova et al., 1999; Dubrov et al., 1998; Ayvazyan, & Mkhitaryan, 2001). Statistical analysis was performed in STATISTICA 6 system (Borovikov, 2003; Khalafyan, 2008; Hill, & Lewicki, 2007; StatSoft, 2013).

Results of the research

3.1. Factor Analysis of life satisfaction indicators

In the first place, consider the basic hypothesis of correlation life satisfaction indicators. Correlation analysis of these indicators revealed significant at different levels (Table 3 ) correlation for different indicators pairs (correlation coefficient r ≥ 0.10 – critical for a group of 400 respondents at a significance level of p = 0.05).

Significant paired correlation coefficients Spearman rank R confirm compliance parametric paired correlation coefficients Pearson r . Typically, R > r , but the differences between them are insignificant. For example, for a pair of 65_8 and 65_9 difference between r = 0.43 and R = 0.52 maximized and p-value insignificant p = 0.1013 (for a group of 400 respondents). This fact allows us to apply parametric cluster analysis of life satisfaction indicators based on the correlation linkage distance (1- r Pearson) as a distance measure for indicators. At the same time as the amalgamation rule used Ward's method. Graphical results clustering life satisfaction indicators are shown in the tree diagram (Fig. 1).

See Full Size >

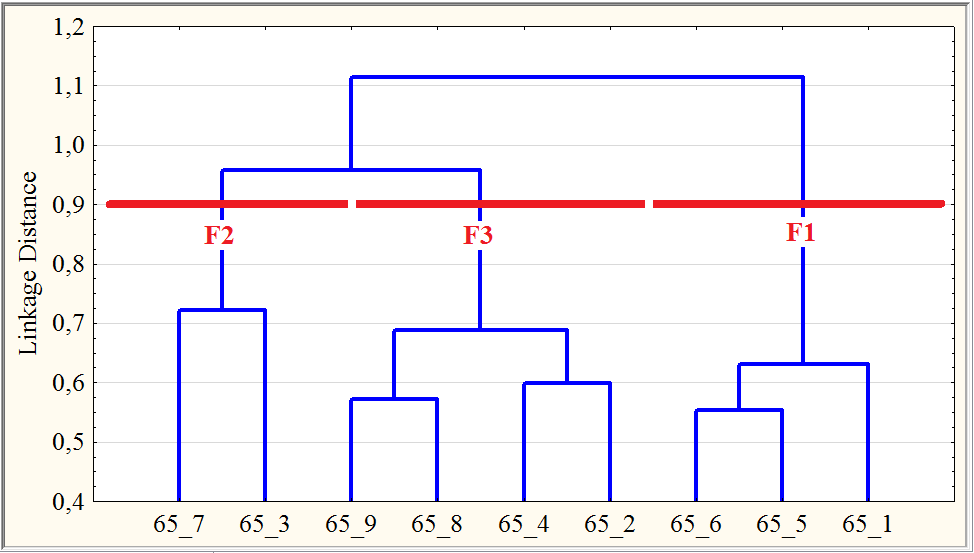
Stable with respect the amalgamation rule (methods Ward, Complete linkage) can be considered the formation of 3-correlation related indicators groups: F1 {1 + 5 + 6}, F2 {3 + 7}, F3 {2 + 4 + 8 + 9}.

Cluster analysis allows to reveal significant (1 – r ≤ 1 – 0,1 = 0.9 – critical for a group of 400 respondents at a significance level p =0.05 allocated in Fig. 1 horizontal dashed line) clusters of life satisfaction indicators, in factors to build a basis of indicators life satisfaction. Using factor analysis by principal components constructed 3-factor model life satisfaction indicators (Table 4 ). Table 4 in bold most significant (basic) factor loadings indicators on the factors that makes it possible to aggregate these indicators to interpret relevant factors. The lower line shows the explained dispersion proportion of this factor (or weighting factors).

Factor of life satisfaction indicators interpret Table 5 .

As a result of factor analysis of 9 initial indicators formed 3 significant factor. On the basis of factorial indicators values further research can be carried out.

3.2. Cluster analysis of the respondents

Consider the following basic hypothesis of the in homogeneities the sample of respondents collectively 3 factorial indicators, in the clustering of all respondents in the constructed factorial space {F1, F2, F3}. During the cluster analysis of the respondents were used Ward's method as a amalgamation rule and Euclidean distance as a linkage distance of the respondents.

Along with tree clustering method was applied the method of K-means conducting the classification of respondents for a given number of groups and for assessing its quality within the ANOVA. In this case, the parametric F-test shows that the difference between the 7 group means highly significant (at p <0.0005) for all factors. Nonparametric Kruskal-Wallis test fully confirms these estimates. Thus, constructed the highly significant according to ANOVA 7-cluster model of the respondents for each factor.

In the framework of ANOVA (by multiple comparisons) can be identified for each factor homogeneous (differing insignificant at the level of significance p > 0.05) cluster group, arranged in descending order of average cluster (Fig. 2).

See Full Size >

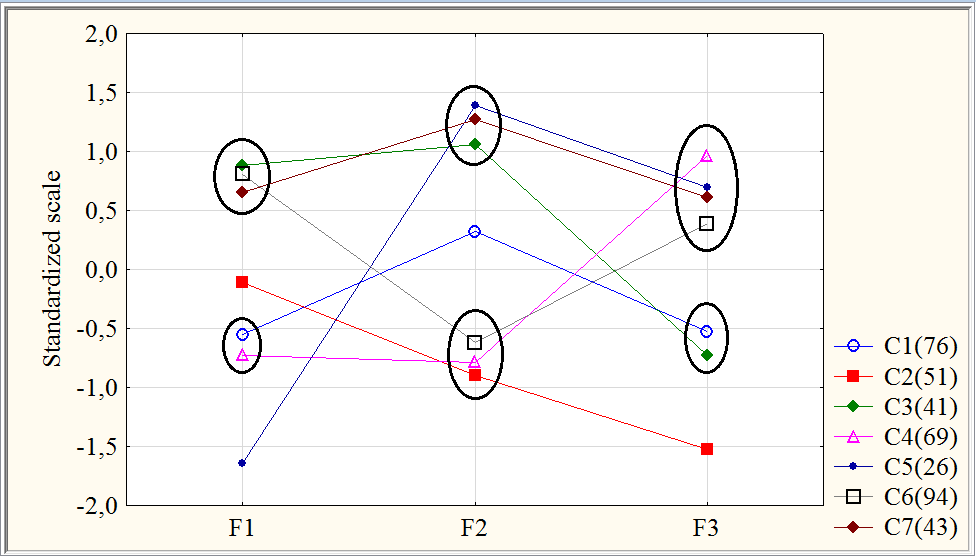
F1: {C3, C6, C7}, {C2}, {C1, C4}, {C5}. In this case C2 differs from C1 statistically significant (0.005 <p <0.050) according to parametric Tukey T-test ( p _T ≈ 0.007), and by rank Kruskal–Wallis test ( p _K-W ≈ 0.012); C2 differs from C7 also statistically significant Kruskal–Wallis test ( p _K-W ≈ 0.006);

F2: {C5, C7, C3}, {C1}, {C6, C4, C2}. In this case C1 differs from C3 and C6 highly significant ( p < 0.0005) according to parametric Tukey T-test, but according to rank Kruskal – Wallis test difference between C1 and C3 is statistically significant (0.005 < p ≈ 0.014 < 0.050);

F3: {C2, C1, C3}, {C5, C4}. In this case C1 differs from C2 and C6 highly significant ( p < 0.0005) according to parametric Tukey T-test, but according to rank Kruskal – Wallis test difference between C1 and C2 is strongly significant (0.0005 < p ≈ 0.044 < 0.0050).

Conducted clustering model allowed a qualitative differentiation of the elderly population of the Tomsk region at factor life satisfaction indicators. According to Figure 2 clusters C5, C7 and C4 (110 respondents) have high indicators of the F2 factor (job satisfaction), but only C7 (43 respondents) high indicators by factor F1 (satisfaction of material wealth and housing) and by a factor F3 (satisfying relationships with family and leisure), while at the C5 (26 respondents) – lower by a factor F1 (dissatisfaction with material wealth and housing), and at C3 (41 respondents) – lower by a factor F3 (dissatisfaction with relationships with family and leisure). Clusters can be further characterize the nominal features of gender, and location. For example, the most highly satisfied all the factorial indicators cluster C7 homogeneous by gender (21 – man and 22 – woman) and less uniform in their place of residence (25 – the city and 18 – village).

Conclusion

A multivariate statistical analysis of the life satisfaction was carried out for older people of the Tomsk region. Was constructed 3-factor model for the life satisfaction indicators based on the correlation and factor analyses of the nine initial indicators. Based on the 3-factor parameters, 400 respondents were compared, and statistically significant differences were determined for all factor parameters. Within the 3-factor space of the life satisfaction, K-means clustering and tree-clustering of 400 respondents was carried out, and the 7-cluster model was constructed for 400 respondents. The high quality of the constructed model was supported by the criteria of the ANOVA (parametricF-test and rank Kruskal–Wallis test). The statistical analysis allowed analyzing a number of hypotheses (about the correlation of parameters and inhomogeneity of respondents) and carrying out the qualitative differentiation of older people of the Tomsk region using the factor parameters of the life satisfaction.

Acknowledgements

This work was performed by the authors in collaboration with Tomsk Polytechnic University within the project in Evaluation and enhancement of social, economic and emotional wellbeing of older adults under the Agreement No.14.Z50.31.0029.

References

1. Ayvazyan, S.A. & Mkhitaryan, V.S. (2001). Probability theory and applied statistics. Moscow: UNITY-DANA, 1. (in Russian)
2. Borovikov, V.P. (2003). Statistica. Art on a computer analysis of the data. St.-Petersburg: Peter. (in Russian)
3. Dubrov, A.M., Mkhitaryan, V.S. & Troshin, L.I. (1998). Multivariate statistical methods. Moscow: Finance and Statistics. (in Russian)
4. Hill, T. & Lewicki, P. (2007). Statistics: Methods and Applications. Tulsa, OK: StatSoft.
5. Ivankina, L.I. & Berestneva, O.G. (2015). Social welfare model. Modern Problems of Science and Education, 1. Retrieved from http://www.science-education.ru/121-r17571. (in Russian)
6. Khalafyan, A.A. (2008). Statistica 6. Statistical analysis of the data. Moscow: Bean-Press. (in Russian)
7. Monastyrny, E.A. et al. (2015). Holistic modeling of complex socio-economic and psycho-physiological effects on the example of the study of well-being of older people. Transfer of technologies – new dimension. Proc. 9th Int. Forum ‘From Science to Business’,. (in Russian)
8. Soshnikova, L.A., Tamashevich, V.N., Uebe, G. & Schaefer, M. (1999). Multivariate statistical analysis in economics. Moscow: UNITY-DANA. (in Russian)
9. StatSoft, Inc. (2013). Electronic Statistics Textbook. Tulsa, OK: StatSoft. Retrieved from http://www.statsoft.com/textbook.