Development and Implementation of a Multi-level System of Training Teachers of Mathematics-computer Science Based on Mathematical and Didactic Modeling Methods, as Well as Interdisciplinary Relations

Abstract

This article deals with the model of mathematics and computer science teachers' training based on the use of mathematical and didactic modeling methods of teaching. As a result of this, prospective teachers should show competence in interdisciplinary studies. This methodology is a special case of the concept of "problem-based learning" (PBL) in mathematics and computer science studies, as well as disciplines where mathematics is applied. The result of the study is that the implementation of interdisciplinary links creates a mental setting which is an effective tool for the development of informative interest of students in the learning process. This setting is based on the problems associated with activities in developing the model. The process of thinking is continuously accompanied by subjective emotions. Imposition of various "sensual" can lead to a change in the MS as a whole and give a boost (inspiration) to mental activity. In the study of educational process by means of MDM, we are required to consider the student and the teacher as constituent parts of the generated model.

Keywords: Physics and mathematics education, methods, teacher training, didactic, simulation, modeling

Mathematics and computer science teachers' training model

1.1.Relevance

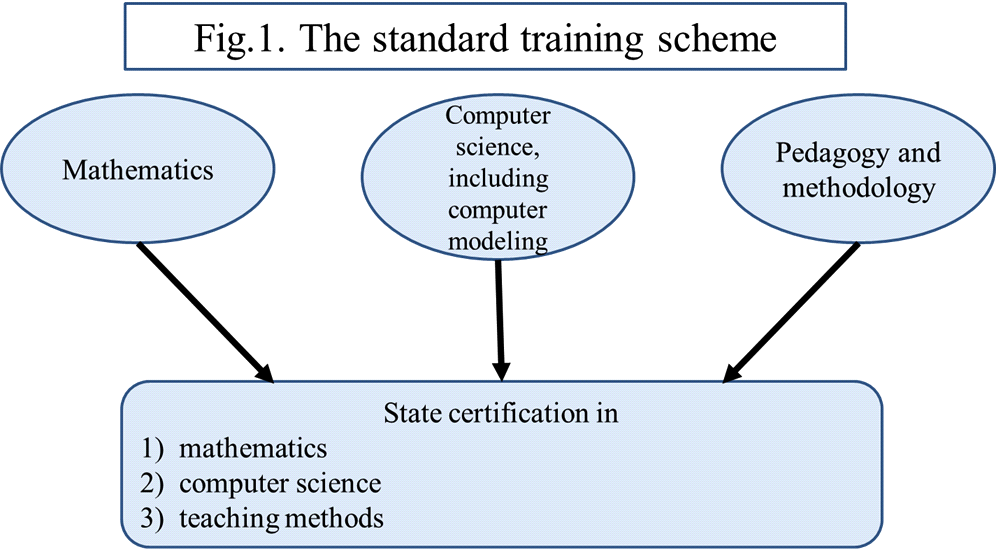
In teaching mathematics, there is an integration problem of fundamental mathematics teaching

methodologies, and the influence of modern information technology. For example, the traditional

teachers training program at the university offers four types of courses, namely:

•Exceptional mathematics (algebra, theory of numbers, mathematical analysis, geometry, etc.);

• Courses related to computer science and computer technology (programming, information technology, etc.);•Courses on methods of teaching mathematics;•Pedagogical and psychological course.

Experience shows that there are insufficient bonds between them. Teachers from different

departments give lectures only on their subjects, and little attention is paid to the establishment of

interdisciplinary relations. As a result, students are not motivated on a deep psychological level to study

mathematics, do not develop skills to work independently, and cannot use the acquired knowledge to

solve specific problems (Fig.1).

See Full Size >

1.2The method of mathematical and didactic modeling

Since 2012 we have commenced the implementation of innovative teachers training methodology in

the departments of mathematics and computer science teachers training in Kazan Federal University.

We named this methodology “mathematical and didactic modeling” (MDM) (Zaripov, & Salekhova,

2012). This name comes from "mathematical - computer modeling" and "didactic engineering"

(Tchoshanov, 2011; Ruthven, 2002). This methodology is the special case of the concept of "problem-

based learning" (PBL) (Graaff, & Kolmos, 2003) in mathematics and computer science studies, as well

as disciplines where mathematics has its own field of application. Mathematical model presented in the

form of computer program represents the end product (goal or result). Thus, the aim of creating

"mathematical model" is the solution of a given problem or task (from various fields of science and

technologies), which originally was reformulated in the language of mathematics. While implementing

MDM the part associated with the "didactic modeling" represents a set of disciplines, and educational

technologies - activities aimed to develop mathematical and computer models by students. It is

important that MDM represents the complete interrelated educational technology, which takes into

account interdisciplinary relations, alongside psychological and motivational factors. Prospective

teachers will use this experience to teach students at schools; this is the main goal of the MDM.

The concept of PBL approach in the application to mathematical education means bringing the

fundamental mathematical knowledge and research to specific mathematical models presented in the

form of computer models and programs that can be used further in various fields of science, technology

and in the daily lives of people. With such approach to "Mathematical Education" it becomes very

important to train mathematics and computer science teachers in acquiring mathematical and computer

skills, as well as the knowledge of mathematics related fields where the use of mathematical apparatus

is dictated by modern scientific trends. First of all, these are the fields as physics, biology, chemistry,

robotics and etc. While training teachers on the interdisciplinary basis, the main focus is solving

problems aimed at building mathematical and computer models. This was the main motivation for this

study. Not just the object of modeling being stimulated, but mathematics and computer science as well,

which act as tools of the cognitive process (Fig.2).

See Full Size >

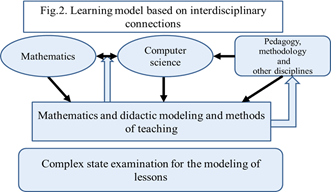
In our baccalaureate program, the «development of interdisciplinary relation on the MDM based

module structure contains three interacting blocks of disciplines:

•The study of objects modeling; in this block, the students' attention is focused on scientific

problems in the disciplines such as, Astronomy, Physics, Biology, Economics, and teaching

methodology.

•The study of mathematical computer programs; in this block of disciplines, the students

nurture skills of working with computers and mathematical software packages.

•The study of mathematical and didactic modeling; in this block of disciplines, the students

nurture skills of using the MDM.

In this paper we consider the experience of using the MDM method in KFU, using the examples of

constructing models from the interdisciplinary fields Astronomy-Physics-Mathematics-Computer

technology. Here we use software «GeoGebra» and «Maple». The strategic objective of

implementation of the designed model is the formation of interdisciplinary mathematics-computer

science competence of prospective teachers. As shown, our experience in this method of training, based

on usage of the MDM is able to create an additional stimulus for independent research activities, and

improve psychological independence of students. Thus develops motivation for a fundamental

mathematical education in general.

Interdisciplinary examples of MDM: Astronomy - Physics - Mathematics - Computer Science

First note that the Baccalaureate program includes courses that can be divided into the following

blocks.

1. The block of mathematical courses is associated with traditional mathematics, such as, analytical

geometry, sections of algebra, mathematical analysis, theory of differential equations, and others.

2. The block of computer science - modern methods of mathematical processing of information,

modern programming languages and computer technologies, computer-mathematics systems in

training, and information technologies in professional work. Students form skills to work with

computers and mathematical software packages.

3. The block of disciplines related to the study of modeling objects. These are naturalistic picture of

the world, introduction to astronomy, mathematical foundations of physics, methodology of teaching

mathematics and computer science. Hence it follows that students have a general idea of the force of

gravity, astronomical objects. Students focus on the scientific issues from the fields of astronomy,

physics, biology, teaching methodology. In this context, "teaching methods" serves as an object of

didactic modeling.

4. The block of mathematical and didactic modeling is based on the disciplines like, Introduction to

mathematical modeling, Mathematical modeling in physics, and Use of mathematical modeling in the

elementary and higher mathematics. Students form skills of mathematical and didactic modeling of the

objects of study, these skills include methods of teaching mathematics and computer science as an

object of modeling.

2.1. Task Definition.

A topic for qualification work was given to an undergraduate to create a mathematical - computer

model of the motion of Halley's comet in two versions. In the first case, he should pose himself as a

scientific leader of high school students. Therefore, it should be based on the available knowledge of

the discipline, and the usage of a simple math program «GeoGebra». In the second case, he can use all

his knowledge of higher mathematics and the mathematical software «Maple». The following values

for complicated option were given: position and velocity vector of the observational data comet

recorded in 1986, at the time of the passage of Halley's comet near Earth. Note that the period of the

motion of Halley's comet is about 80 - 89 years. More accurate determination of its trajectory is a

scientific problem which is not completely solved.

The goal of this research is to implement interdisciplinary links by means of development of

cognitive interest for astronomy, physics and mathematics. The object of research, on the one hand, is

to obtain celestial mechanics equations and mathematical modeling, and on the other hand, to develop

teaching methods based on MDM. The hypothesis of the study is that the implementation of

interdisciplinary links is an effective tool for the development of cognitive interest of students in the

learning process.

Let`s discuss briefly the main components of constructing a model in our thesis.

2.2. A model with physical and mathematical point of view.

A model with physical and mathematical point of view includes the repetition of Newton's law of

universal gravitation.

The motion of two bodies takes place under the action of two forces, $\mathrm{}\stackrel{1}{F_{12}}$ and $\mathrm{}\stackrel{1}{F_{12}}$equal in

magnitude but oppositely directed. The magnitude of these forces is determined by the masses 1and

2, vector length $\stackrel{1}{r}=\frac{1}{r_2}-\frac{1}{r_1}$ connecting points of centers of gravity: $\mathrm{}\left|\frac{r}{F_{12}}\right|=\left|\frac{r}{F_{21}}\right|=\frac{G{m}_1{m}_2}{r^2}$ where- gravitational constant. Taking into account Newton's second

law, proceeding to a coordinate system, the origin of which coincides with the center of mass, we

obtain the second order differential equation:

$\frac{d^2\frac{r}{r}}{d{t}^2}=-\frac{GM}{r^3}{r}^{\mathrm{r}},\text{where}M=m_1+m_2,t$ - time parameter. (1)

After obtaining the equation (1) there are remain purely mathematical calculations to solve this

equation. First, we should prove that the motion described by equation (1) is flat. Then we proceed to

the polar coordinate system {,ϕ}, equations once integrated and reduced to the form:

$r\left(f\right)=\frac{p}{1+e\mathrm{c}\mathrm{o}\mathrm{s}?(f-a)}$ )

$\frac{df}{dt}=\frac{h}{\left(r\right(f){)}^2};p=\frac{h^2}{GM},\text{where}\mathrm{h},e,a\text{-integration constant.}$

To find the relation $\phi =\phi \left(t\right)$, the remaining differential equation can be integrated numerically.

Our undergraduate remembers that the first of the equations (2) is the second-order curve

equation,

Proceeding to the Cartesian coordinate system we get

$\left\{\begin{array}{l}{x}^{\mathrm{\text{'}}}\left(\phi \right)=r\left(\phi \right)\mathrm{c}\mathrm{o}\mathrm{s}\phi -x_{\mathrm{0}}\\ y^{\mathrm{\text{'}}}\left(\phi \right)=r\left(\phi \right)\mathrm{s}\mathrm{i}\mathrm{n}\phi \end{array}\right.$

The equation of the trajectory can be written in explicit form. We prove, for the case (e ≤1), if

instead of parameters p, e enter new parameters a and b

$p=\frac{b^{\mathrm{2}}}{a},e=\pm \sqrt{\mathrm{1}-k_e^{\mathrm{2}}},\text{where}{k}_e=\frac{b}{a}=\mathrm{1}$ then the following equation holds

$\frac{x^{\mathrm{\text{'}}\mathrm{2}}}{a^{\mathrm{2}}}+\frac{y^{\mathrm{\text{'}}\mathrm{2}}}{b^{\mathrm{2}}}=\mathrm{1},\text{if}{x}_{\mathrm{0}}=-ae.$ Here, the constant e

- is the eccentricity of ellipse. Thus canonical

equation of the ellipse is obtained.

The purpose of physical and mathematical components of the thesis is to link the higher

mathematics with math that can be easily understood by high school student. For example, the study of

the equation of the ellipse is quite acceptable for high school students. On the other hand, the

undergraduate (prospective teacher) has inner confidence in a wider sense of the problem, that he must

set it out to a schoolboy in a simplified form. Because he has done all the math problems on his own.

Using these formulas has proved Kepler's three laws.

of the model is the most complex.

Although students learn computer software system while studying at baccalaureate, to solve this

problem, repetition and selection of particular subprograms and commands associated with the

numerical solution of differential equations and construction of graphics and animation is required.

«Maple» and «GeoGebra» mathematical programs were selected (for the model being created by a

school boy).

See Full Size >

During the development of computer program an undergraduate went through the following work

stages.

Developing a program to demonstrate the motion of the planets of the solar system, taking into

account the real physical parameters of the planets (speed, eccentricity, aphelion distance, and other

parameters). Development of a software module Eps: = (a, e, G_M, theta_0, t_0, col_orb, c_pl,

r_pl_20, r_sol, c_sol). It is necessary to enter parameters of celestial bodies: a - aphelion distance, e -

eccentricity, G_M - parameter of gravitational mass of the sun, {theta_0, t_0} - initial conditions, the

colour images of the planet's orbit, and others. This module with high accuracy displays motion

animation of predetermined celestial object around the central body (the Sun).

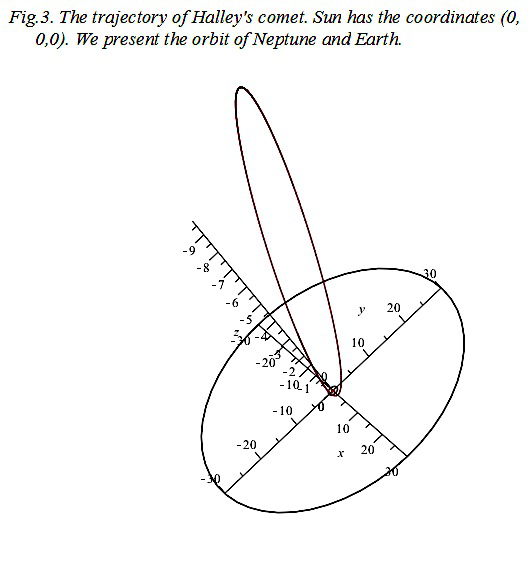
Developing a program for modeling the motion of Halley's comet, with respect to the solar

system. The task was complicated by the fact that this movement is not in the plane of the ecliptic (the

plane of the major planets in the solar system), and is inclined to the plane at an angle (Fig.3.).

Therefore, the problem had to be solved numerically.

See Full Size >

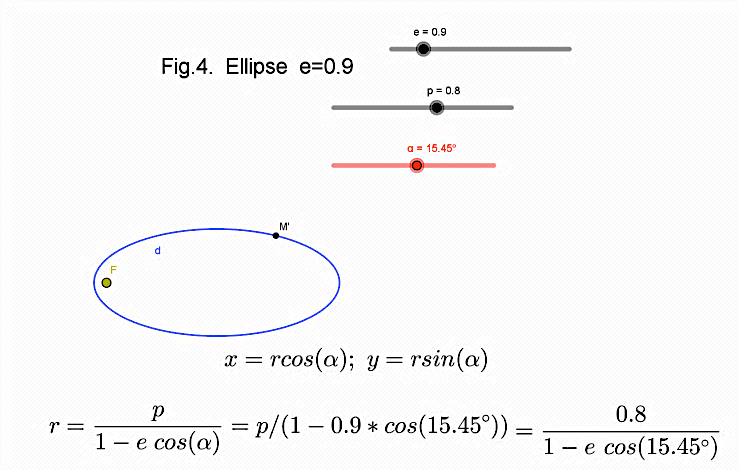
In order to prepare materials for school children on modeling in astronomy, models of the motion

of celestial bodies around the central body using «GeoGebra» software were developed (fig.4.).

Animation occurs due to change of the third slider. It is important to note this about eccentricity

changes, when e = 1 - the trajectory changes into parabolic orbit, and changes into hyperbolic orbit,

when e> 1. In addition, the undergraduate has prepared material on mathematics and astronomy, which

are available for high school students. The attempt to teach a student to build the model using the

«GeoGebra» software was successful.

Thus, our experience proves that the MDM approach is a working tool that improves the quality of

students learning.

Analysis of the study results

First of all, the results of the above mentioned methodological experience and observation are the

increase of knowledge and skills (as a branch of science related to the MDM method and the model

itself) for all project participants. This is what we wanted. We would like to emphasize the importance

of a comprehensive review of MDM method and simulation didactic part. The didactic side is much

deeper and covers the psychological aspects of the process. The result of the study is that the

implementation of interdisciplinary links creates a mental setting (MS) which is an effective tool for the

development of informative interest of students in the learning process. This setting is based on the

problems associated with activities in developing the model. However, this is only the beginning. As

soon as he begins to study the problem, he encounters the history of the discovery of Halley's comet

and subsequent observations of the celestial body, as well as the history of the individual German

mathematician and astronomer, discoverer of the laws of the solar system Johannes Kepler. The

historical theme in the thesis does not affect the outcome directly. At the same time historical topics

affect the content and the structure of the MS, adding a sensual component, which through the work of

the thought process adds new colours and expands the subjective awareness. Different layers of

perception associated with the process of working to develop a specific model superimpose on personal

feelings. Besides historical themes of perception, which is a subsidiary, we were able to distinguish the

logical (mathematical), physical or astronomical (ideas about the laws of motion of celestial bodies)

components of MS. The process of thinking is continuously accompanied by subjective emotions.

Imposition of various "sensual" can lead to a change in the MS as a whole and give a boost (inspiration)

to mental activity. In the study of educational process by means of MDM, we are required to consider

the student and the teacher as constituent parts of the generated model.

References

• Graaff, E. &, Kolmos, A. (2003). Characteristics of Problem-Based Learning. J. Engng Ed. - Vol.

• 19(5), 657–662.

• Zaripov, F. & Salekhova, L. (2012). Mathematical modeling and teaching as the basis for the training of teachers’ double profile (mathematics and computer science). KFU. 47. The electronic version: http: //libweb.ksu.ru/ebooks/publicat/05_A5m-000001.pdf.

• Ruthven, K. (2002). Linking researching with teaching: Towards synergy of scholarly and craft knowledge. Handbook of international research in mathematics education/ Editor Lyn D. English. London: LEA, 581-598.

• Tchoshanov, M. (2011.) Didactics and Engineering, M.: Bean. Knowledge Laboratory. 248.