A Novel Binary DE Based on the Binary Search Space Topology

Abstract

Differential evolution is known as a simple and well-argued evolutionary algorithm that demonstrates the high performance in many hard black-box optimization problems with continuous variables. The main feature of differential evolution is the difference-based mutation. The mutation explores the search space using the distribution of points in the population and usually can well adapt to the objective function landscape. There exist some modifications of differential evolution for the binary search space. The proposed approach involves the understanding of the binary space topology for developing a better analogue of the difference-based mutation. We have compared the proposed binary differential evolution algorithm with the standard binary genetic algorithm using a set of binary test problems, including hard deceptive problems. The preliminary experimental results shows that new binary differential evolution is a competitive search algorithm and outperforms the binary genetic algorithm in reliability for some problems but yields it in the required number of function evaluations. The proposed approach for developing mutation in DE can be expanded to all other mutation schemes for increasing the performance.

Keywords: Binary differential evolution, genetic algorithm, black-box optimization

Introduction

Differential evolution (DE) is known as a simple and well-argued evolutionary algorithm (EA) that demonstrates the high performance in many hard black-box optimization problems with continuous variables (Storn & Price, 1997). DE demonstrates the high performance even in its originally proposed form. Nevertheless, many modifications for different classes of optimization problems have been proposed. Many of DE-based approaches have become competition winners and are state-of-the-art (Molina et al., 2018, Stanovov et al., 2021). Unlike many EAs, DE uses another evolutionary cycle. In the general EA cycle, selection is used for defining the fittest individuals for mating. Then crossover produces an offspring that contains a recombination of parents’ genes. Mutation is used as an additional operator for preventing the premature convergence and makes random and usually weak changes in genes of the offspring. The main feature of DE is the difference-based mutation. The operator plays the most important role in the search process and is applied before crossover and selection for generating a new random solution based on the distribution of the population in the search space. Such mutation usually can well adapt to the landscape of the objective function, identifies regularities and separable components, can walk along ravines. The benefits make DE attractive to work with other search spaces, and especially with the binary space.

There exist some modifications of differential evolution for the binary search space. The standard approach uses DE with continuous variable in $[0,1]$, which are rounded to $0$ or $1$. The simple rounding can be substituted by the algorithm from the binary PSO, which defines 0 or 1 by evaluating the sigmoid function from the velocity of changes in genes (Pampara et al., 2006). The angle modulated DE (AMDE) makes use of angle modulation, a technique derived from the telecommunications industry, to implement a mapping between binary and continuous spaces (Engelbrecht & Pampara, 2007). Many approaches operate the binary space directly and design new mutation schemes for the representation (Chen et al., 2015; Deng et al., 2011; Peng et al., 2016). Some alternative approaches don’t design analogs of operators in continuous DE, but develop new operators while maintaining the general DE’s scheme (Banitalebi et al., 2016; Wang et al., 2012).

In this study, we propose a new approach that involves the understanding of the binary space topology for developing a better analogue of the continuous difference-based mutation. The proposed binary difference-based mutation involves such elements of the binary space as the Boolean hypercube, the neighbourhood of a binary vector, and the shortest path. The proposed binary differential evolution algorithm has been compared with the standard binary genetic algorithm using a set of binary test problems, including hard deceptive problems. The experimental results shows that new binary differential evolution is a competitive search algorithm and outperforms the binary genetic algorithm in reliability for some problems but yields it in the required number of function evaluations. At the same time, the results are preliminary, because the proposed approach for developing mutation in DE can be expanded to all other mutation schemes and state-of-the-art self-adaptive approaches for increasing the performance.

The rest of the paper is organized as follows. Section 2 describes the problem statement and the proposed approach. Sections 3 presents experimental setups and the experimental results. In conclusion, the proposed methods and the obtained results are summarized, and some further research is suggested.

Problem Statement

The standard DE algorithm solves the continuous global optimization problem (1), where the objective function is assumed to be a black-box model:

$f\left(\mathit{x}\right)\to \underset{\mathit{x}\in {\mathbb{R}}^n}{\mathrm{m}\mathrm{i}\mathrm{n}},\mathrm{}f:\mathit{x}\to \mathbb{R}$,(1)

here $\mathit{x}=(x_{\mathrm{1}},\dots ,x_n)$ and $\forall i:x_i\in S\subseteq {\mathbb{R}}^n$, usually ${lb}_i\le x_i\le r{b}_i$ with left ( $lb$) and right ( $rb$) bounds.

Many real-world optimization problems use binary decision variables, but the quality of a solution is still estimated using a real value. Binary variables can be also the result of encoding of mixed-type variables or the result of the discretization of continuous variables. In this case, we deal with pseudo-Boolean optimization that uses the following formal problem statement is (2):

$f\left(\mathit{x}\right)\to \underset{\mathit{x}\in {\left\{\mathrm{0,1}\right\}}^n}{\mathrm{m}\mathrm{i}\mathrm{n}},\mathrm{}f:\mathit{x}\to \mathbb{R}$,(2)

here $\mathit{x}=(x_1,x_2,\dots ,x_n)$ is a Boolean vector of $n$ coordinates, $n\in {\mathbb{N}}^{+}$, $f$ is an objective function. There are no assumptions on the type and properties of the objective function, thus it is considered as a black-box model.

Research Questions

One of approaches for understanding and analysing the topology of the binary search space is the representation using an $n$-dimensional Boolean hypercube (Björklund et al., 2004; Boros & Hammer, 2002). Let’s make some important definitions.

Let $d_H\left({\mathit{x}}_i,{\mathit{x}}_j\right)=\underset{k=1}{\overset{n}{\sum }}\left|x_{ik}-x_{jk}\right|$ is the Hamming distance between two binary vectors ${\mathit{x}}_i$ and ${\mathit{x}}_j$.

Let $N_1\left({\mathit{x}}_i\right)=\left\{\mathit{x}:d_H\left(\mathit{x},{\mathit{x}}_i\right)=1\right\}$ is a set of 1-neighbour vectors. A set of k-neighbour vectors can be defined at the same manner: $N_k\left({\mathit{x}}_i\right)=\left\{\mathit{x}:d_H\left(\mathit{x},{\mathit{x}}_i\right)=k\right\}$.

All binary vectors are vertices of the Boolean hypercube. Each pair of 1-neighbour vectors defines an edge of the hypercube.

Let a set $path\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right)=\{{\mathit{x}}_{\mathrm{0}},{\mathit{x}}_{\mathrm{1}},\dots ,{\mathit{x}}_{m-\mathrm{1}},\mathrm{}{\mathit{x}}_m\}$ is a path from a vertex ${\mathit{x}}_{\mathrm{0}}$ to a vertex ${\mathit{x}}_m$, then $\forall {\mathit{x}}_i,{\mathit{x}}_{i+\mathrm{1}}\in path\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right):{\mathit{x}}_{i+\mathrm{1}}\in N_{\mathrm{1}}\left({\mathit{x}}_i\right)$. The length of the path is equal to $\left|path\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right)\right|=m$.

If $d_H\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right)=k$ and $\left|path\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right)\right|=k$, when $pat{h}_s\left({\mathit{x}}_{\mathrm{0}},{\mathit{x}}_m\right)$ is the shorted path $.$

If $d_H\left({\mathit{x}}_0,{\mathit{x}}_m\right)>1$, there are multiple shortest paths from ${\mathit{x}}_0$ to ${\mathit{x}}_m$.

Now let’s consider the general scheme of a DE algorithm (see Algorithm 1). It contains three main steps, namely the difference-based mutation, crossover, and selection.

Algorithm 1. DE

1Set the population size N, the scaling factor F, and the crossover probability CR.

2Initialize population of random solutions {x_1,x_2,…,x_N } and evaluate their fitness values.

3while the termination criteria are not met do

4for i=1,…,N do

5Generate a mutant vector v_i using one of mutation schemes.

6Perform crossover of x_i and v_i and get a trial vector u_i.

7Perform selection. If the trial vector u_i is better than x_i, save u_i in the population.

8for end

9while end

The following notation for choosing specific DE’s operator is used: $DE/M/D/C$, where $M$ is a mutation strategy, $D$ is the number of difference vectors in the mutation scheme, $C$ is a type of crossover. Let’s discuss the most popular and simple DE: $DE/rand/1/bin$, which uses mutation with random vectors, only one difference vector, and the binominal crossover operator. The DE algorithm was proposed for continuous optimization problems and the mutation scheme for $rand/1$ is defined as (3):

${\mathit{v}}_{\mathit{i}}={\mathit{x}}_{r\mathrm{1}}+F\cdot ({\mathit{x}}_{r\mathrm{2}}-{\mathit{x}}_{r\mathrm{3}})$,(3)

here $r1$, $r2$, and $r3$ are indexes of different random vectors from the population, i.e. $r1\ne r2\ne r3\ne i$, and $F$ is the scale factor. The difference-based mutation produces a new point ${\mathit{v}}_{\mathit{i}}$ in the search space by moving from ${\mathit{x}}_{r1}$ in the direction from ${\mathit{x}}_{r3}$ to ${\mathit{x}}_{r2}$ at the distance defined by $F$ (if $F=1$, the distance is equal to the length of $({\mathit{x}}_{r2}-{\mathit{x}}_{r3})$). Figure 1 demonstrates an example of such mutation.

See Full Size >

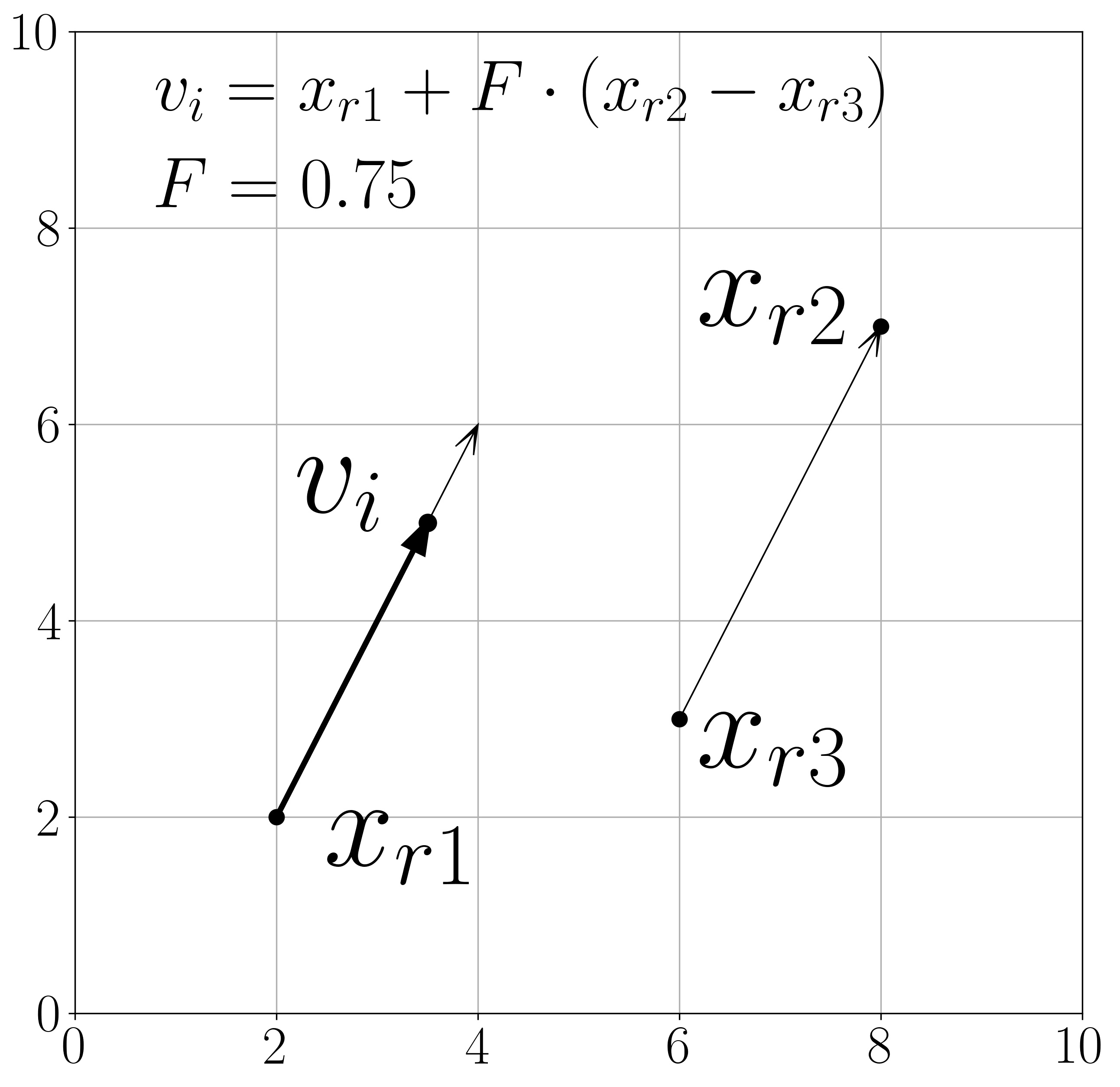
Purpose of the Study

The purpose of the study is the development of a way for building a mutant vector in the binary search space that uses the conception similar to mutation in the continuous search space.

First, we will define the direction from ${\mathit{x}}_{r3}$ to ${\mathit{x}}_{r2}$ in the binary space. By analogy with the continuous search space, we must define the shortest path from ${\mathit{x}}_{r3}$ to ${\mathit{x}}_{r2}$. This can be done using definition 4. Because of several shortest paths in the binary space, we must choose one of them. We can do it at random because of the mutation conception. Second, we must evaluate a point along the chosen direction at the distance defined by the scaling factor $F$. Because of the discrete search space, the point on the path can be defined as a point that belongs to the neighbourhood $N_l\left({\mathit{x}}_{r3}\right)$ (definition 2), where $l\in \{\mathrm{0,1},\dots ,d_H\left({\mathit{x}}_{r2},{\mathit{x}}_{r3}\right)\}$ is defined using $F$. It is obvious that $N_0\left({\mathit{x}}_{r3}\right)=\left\{{\mathit{x}}_{r3}\right\}$ and $N_{d_H\left({\mathit{x}}_{r2},{\mathit{x}}_{r3}\right)}\left({\mathit{x}}_{r3}\right)=\left\{{\mathit{x}}_{r2}\right\}$. We can define $l$ by rounding up the result of the following product (4):

$l=⌈F\cdot d_H\left({\mathit{x}}_{r\mathrm{2}},{\mathit{x}}_{r\mathrm{3}}\right)⌉,\mathrm{}F\in \left(\mathrm{0,1}\right]$.(4)

Thereby, the $\left(F\cdot ({\mathit{x}}_{r2}-{\mathit{x}}_{r3})\right)$ component of the difference-based mutation can be defined as a random vector that belongs to the shortest path from ${\mathit{x}}_{r3}$ to ${\mathit{x}}_{r2}$ and is located on the distance $l$ from ${\mathit{x}}_{r3}$ (5):

${\mathit{x}}_d\in N_l\left({\mathit{x}}_{r\mathrm{3}}\right)\cap pat{h}_S({\mathit{x}}_{r\mathrm{2}},\mathrm{}{\mathit{x}}_{r\mathrm{3}})$.(5)

Finally, we need to make the movement from ${\mathit{x}}_{r1}$ in the direction defined by ${\mathit{x}}_d$. For the binary space the movement means that a mutant vector ${\mathit{v}}_{\mathit{i}}$ will be in $N_l\left({\mathit{x}}_{r1}\right)$ and its $l$components will differ in the same positions as components differ in ${\mathit{x}}_{r3}$ and ${\mathit{x}}_d$. Such a way will save components, which stay unchanged in the shortest path, by analogy with the movement in the continuous space if the direction $({\mathit{x}}_{r2}-{\mathit{x}}_{r3})$ is parallel to some of coordinate axes. The whole algorithm for performing the $rand/1$ mutation in the binary space can be defined using properties of the exclusive disjunction (XOR) operation (6):

${\mathit{v}}_{\mathit{i}}\mathbf{=}{\mathit{x}}_{r\mathrm{1}}\oplus \left({\mathit{x}}_d\oplus {\mathit{x}}_{r\mathrm{3}}\right)$.(6)

In the same manner, one can evaluate all the rest of mutation schemes. In this study, we will also test the $current-to-best/1$ scheme (7)-(8), which is reported as one of the best non-adaptive mutation schemes (Mohamed et al., 2021) and $rand/2$ as it produces better diversity in the population (9)-(10).

${\mathit{v}}_{\mathit{i}}\mathbf{=}{\mathit{x}}_i\oplus \left({\mathit{x}}_{d_{\mathrm{1}}}\oplus {\mathit{x}}_i\right)\oplus \left({\mathit{x}}_{d_{\mathrm{2}}}\oplus {\mathit{x}}_{r\mathrm{2}}\right)$,(7)

${\mathit{x}}_{d_{\mathrm{1}}}\in N_l\left({\mathit{x}}_i\right)\cap pat{h}_s({\mathit{x}}_{best},\mathrm{}{\mathit{x}}_i)$, ${\mathit{x}}_{d_{\mathrm{2}}}\in N_l\left({\mathit{x}}_{r\mathrm{2}}\right)\cap pat{h}_S({\mathit{x}}_{r\mathrm{1}},\mathrm{}{\mathit{x}}_{r\mathrm{2}})$,(8)

here ${\mathit{x}}_i$ is a vector from the population that is used for building a trial vector, ${\mathit{x}}_{best}$ is the best-found solution, $r1$, $r2$ are indexes of different random vectors from the population, i.e. $r1\ne r2\ne i$.

${\mathit{v}}_{\mathit{i}}\mathbf{=}{\mathit{x}}_{r\mathrm{1}}\oplus \left({\mathit{x}}_{d_{\mathrm{1}}}\oplus {\mathit{x}}_{r\mathrm{3}}\right)\oplus \left({\mathit{x}}_{d_{\mathrm{2}}}\oplus {\mathit{x}}_{r\mathrm{5}}\right)$,(9)

${\mathit{x}}_{d_{\mathrm{1}}}\in N_l\left({\mathit{x}}_{r\mathrm{3}}\right)\cap pat{h}_s({\mathit{x}}_{r\mathrm{3}},\mathrm{}{\mathit{x}}_{r\mathrm{2}})$, ${\mathit{x}}_{d_{\mathrm{2}}}\in N_l\left({\mathit{x}}_{r\mathrm{5}}\right)\cap pat{h}_S({\mathit{x}}_{r\mathrm{5}},\mathrm{}{\mathit{x}}_{r\mathrm{4}})$,(10)

here $r1$, …, $r5$ are indexes of different random vectors from the population, i.e. $r1\ne r2\ne r3\ne r4\ne r5\ne i$.

We don’t need to make any changes in the crossover and selection operators because they don’t depend on the search space properties.

Research Methods

The proposed approach has been implemented using C++ in the multi-thread mode for parallel computations using multicore CPUs. We have chosen the following set of test problems: the $OneMax$ problem with $n=100$ for evaluating the general ability of convergence, 6 hard massively multimodal and deceptive functions [we use the original notation $f_{11}$, …, $f_{16}$ as in (Yu & Suganthan, 2010)] with $n$ equal to $30$, $30$, $24$, $30$, $30$, and $40$.

Binary DE have been tested with various combinations of parameters $F$ and $Cr$ from the following sets: $F=\{0.1,0.25,\mathrm{0.5,0.75,0.9}\}$ and $Cr=\{0.1,0.25,\mathrm{0.5,0.75,0.9}\}$. The performance of binary DE has been compared with the standard binary genetic algorithm (GA). Binary GA have been tested with various settings the following sets: the type of crossover = {one-point, two-point, uniform} and the probability of mutation = { $1/3n,1/n,3/n$}.

The budget of function evaluations ( $maxFEs$) and its distribution in generations are: $maxFEs=20000$, the population size ( $popSize$) is 100, and the number of generations ( $maxGens$) is 200 for $OneMax$; $maxFEs=50000$ (as it is proposed by authors of the benchmark), and $popSize/maxGens=\left\{100/500,250/200\right\}$ for $f_{11}$, …, $f_{16}$. The number of independent runs for each combination of parameters for each test function is 100. The performance measures are the rate of successful runs ( $SR$) when the global optimum was found (an estimation of the probability of finding the global solution) and the average number of $FEs$ before the global optimum was found (only for successful runs).

Findings

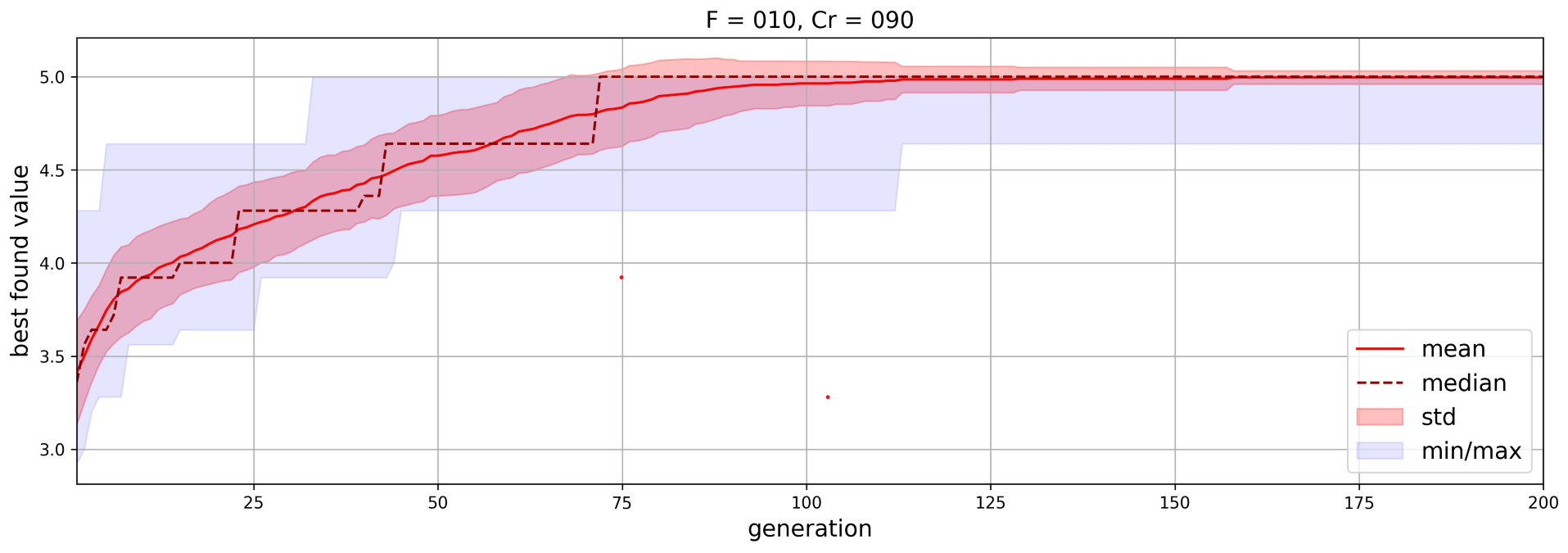
The experimental results for the best settings of each algorithm are presented in Table 1. An example of the typical convergence plot for $f11$ averaged over 100 runs is shown in Figure 2.

See Full Size >

Conclusion

In the study, we have proposed a novel binary DE that uses the difference-based mutation in the binary search space by analogy how it operates in the continuous space. The mutation operator uses such definitions as the neighbourhood, the shortest path over the Boolean hypercube. The preliminary experimental results have shown that the proposed approach is able to solve hard global pseudo-Boolean optimization problems and for many of considered problems the success rate of finding the global optimum is 100%. At the same time, we can see that the approach is slower that GA, which uses random mutation. We assume that binary DE can find a more accurate solution for large-scale problem with the limited budget of FEs, because it monotonically converges instead of randomly generating new points. In this study, we have tested only three simple schemes of mutation. State-of-the-art DE algorithms use many additional mechanisms such as restarts, the control of the population size, the self-adaptive control of parameters $F$ and $Cr$, and self-adaptive mutation. In out further work, we will investigate one of the best DE approach SHADE in the binary space and will extend the test problem set with known benchmarks.

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.

References

• Banitalebi, A., Abd Aziz, M. I., & Aziz, Z. A. (2016). A self-adaptive binary differential evolution algorithm for large scale binary optimization problems. Information Sciences, 367, 487-511.

  Google Scholar

  Crossref

• Björklund, H., Sandberg, S., & Vorobyov, S. (2004). Complexity of Model Checking by Iterative Improvement: The Pseudo-Boolean Framework. In M. Broy, & A. V. Zamulin (Eds), Lecture Notes in Computer Science (Vol. 2890, pp. 381-394). https://doi.org/10.1007/978-3-540-39866-0_38

• Boros, E., & Hammer, P. L. (2002). Pseudo-Boolean optimization. Discrete Applied Mathematics, 123(1-3), 155-225.

  Google Scholar

  Crossref

• Chen, Y., Xie, W., & Zou, X. (2015). A binary differential evolution algorithm learning from explored solutions. Neurocomputing, 149, 1038-1047.

  Google Scholar

  Crossref

• Deng, C., Zhao, B., Yang, Y., Peng, H., & Wei, Q. (2011). Novel binary encoding differential evolution algorithm. In Y. Tan, Y. Shi, Y. Chai, & Wang, G. (Eds), Advances in Swarm Intelligence: Second International Conference, ICSI 2011, Chongqing, China, June 12-15, 2011, Proceedings, Part I 2 (pp. 416-423). Springer.

  Google Scholar

  Crossref

• Engelbrecht, A. P., & Pampara, G. (2007). Binary differential evolution strategies. In 2007 IEEE congress on evolutionary computation (pp. 1942-1947). IEEE.

  Google Scholar

  Crossref

• Mohamed, A. W., Hadi, A. A., & Mohamed, A. K. (2021). Differential Evolution Mutations: Taxonomy, Comparison and Convergence Analysis. IEEE Access, 9, 68629-68662.

  Google Scholar

  Crossref

• Molina, D., LaTorre, A., & Herrera, F. (2018). SHADE with iterative local search for large-scale global optimization. In 2018 IEEE congress on evolutionary computation (CEC) (pp. 1-8). IEEE.

  Google Scholar

  Crossref

• Pampara, G., Engelbrecht, A. P., & Franken, N. (2006, July). Binary differential evolution. In 2006 IEEE international conference on evolutionary computation (pp. 1873-1879). IEEE.

  Google Scholar

  Crossref

• Peng, H., Wu, Z., Shao, P., & Deng, C. (2016). Dichotomous Binary Differential Evolution for Knapsack Problems. Mathematical Problems in Engineering, 1-12.

  Google Scholar

  Crossref

• Stanovov, V., Akhmedova, S., & Semenkin, E. (2021). NL-SHADE-RSP Algorithm with Adaptive Archive and Selective Pressure for CEC 2021 Numerical Optimization. IEEE Congress on Evolutionary Computation (CEC) (pp. 809-816). IEEE.

  Google Scholar

  Crossref

• Storn, R., & Price, K. (1997). Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. Journal of Global Optimization, 11, 341-359.

  Google Scholar

  Crossref

• Wang, L., Fu, X., Mao, Y., Menhas, M. L., & Fei, M. (2012). A novel modified binary differential evolution algorithm and its applications. Neurocomput, 98, 55-75.

  Google Scholar

  Crossref

• Yu, E. L., & Suganthan, P. N. (2010). Ensemble of niching algorithms. Information Sciences, 180(15), 2815-2833.

  Google Scholar

  Crossref