Abstract
The article explores the possibility of using the entropy characteristics of the time series of the electroencephalogram signal for the task of automatically detecting epileptic seizures by electroencephalogram recording. Because of the brain is a complex distributed active environment, self-oscillating processes take place in it. These processes can be judged by the EEG signal, which is a reflection of the total electrical activity of brain neurons. Based on the assumption that during an epileptic seizure, excessive synchronization of neurons occurs, leading to a decrease in the dynamic complexity of the electroencephalographic signal, entropy can be considered as a parameter characterizing the degree of systemic chaos. The sample entropy method is a robust method for calculating entropy for short time series. In this work, the sample entropy was calculated for an electroencephalographic record of a patient with epilepsy obtained from an open set of clinical data. The calculation was made for different sections of the recording, corresponding to the norm and pathology (generalized epileptic seizure). It has been shown that the entropy characteristics of the electroencephalogram signal can serve as informative features for machine learning algorithms to automatically detect signs of neurological pathology associated with epilepsy.
Keywords: Electroencephalogram data analysis, EEG, automatic seizure detection, entropy, machine learning
Introduction
Machine learning is an interdisciplinary field in which the mathematical apparatus of various disciplines is widely used, such as linear algebra, methods of probability theory, statistics, dynamical systems theory, modern optimization methods, and many others. The accumulation of large volumes of biomedical data has provided new opportunities for the development of algorithms for automatic data analysis and the creation of high-performance software for their automatic interpretation. Data mining algorithms make it possible to search for and reveal hidden and non-trivial patterns in data and gain new knowledge about the objects under study (Kazakovtsev et al., 2020). Currently, it is impossible to imagine the further development of medical technologies without the use of machine learning technologies. Therefore, the demand for software products that can facilitate manual data processing or perform it fully automatically in real time is constantly growing.
This article discusses the possibility of using entropy as a measure of signal complexity as an informative feature for machine learning algorithms in the task of automatically detecting pathologies associated with epilepsy according to electroencephalogram (EEG) recording data.
Problem Statement
Epilepsy is a group of neurological disorders characterized by involuntary seizure activity, which is reflected in the recording of the electroencephalogram (Fergus et al., 2015).
An electroencephalogram is a non-invasive, inexpensive, and extremely informative method for studying the functional state of the brain, which is widely used to diagnose a number of diseases, such as stroke, epilepsy, and other disorders of the nervous system (Obeid & Picone, 2018). Despite the emergence of such modern methods of brain research as CT and MRI, the electroencephalogram still remains important, and for some diseases, such as epilepsy, an indispensable tool for studying the state of the nervous system both in scientific research and in clinical practice. An electroencephalogram is a record of electrical potentials resulting from the total electrical activity of billions of neurons in the brain, recorded using special electrodes from the surface of the patient's head. The use of EEG in clinical practice involves manual analysis of continuous EEG recordings up to 72 hours long, which is a laborious and expensive task that requires the involvement of by board-certified neurologists (Shah et al., 2018). Therefore, the development of methods and algorithms capable of automatically detecting signs of seizure activity from the EEG recording, with sufficient accuracy and speed for clinical applications, is an urgent task. Quite often, in machine learning problems, finding suitable features is no less difficult than actually solving it (Goodfellow et al., 2018). The choice of the most informative features is a key problem in the development of algorithms for automatic analysis of EEG data.
Purpose of the Study
One of the properties of complex systems, which include the brain, is a high ability to adapt to environmental changes. There are many examples of the colossal adaptive ability of the brain, when the loss of sufficiently large parts of it is compensated by the work of others. Such high adaptive capabilities are characteristic of chaotic systems capable of being in a non-equilibrium state with a high degree of uncertainty in the short term, but possessing, however, long-term stability. Reducing the complexity of such systems leads to a decrease in their adaptive capabilities (Peters, 2000). The purpose of this study is to show that when an epileptic seizure occurs, as a result of excessive synchronization of the work of brain neurons, the dynamic complexity of the EEG signal decreases, which is reflected in a change in the signal entropy value.
Research Questions
The main question of the study is the question of whether the value of the entropy of the signal changes when an epileptic seizure occurs. If the signal entropy value for the recording sections corresponding to an epileptic seizure differs from the normal recording, then the entropy can be used as an informative feature for machine learning algorithms.
Research Methods
The Emergence of brain rhythms based on the theory of dynamical systems
The brain is a distributed environment consisting of many active elements of the same type which are neurons. The combination of these elements, interacting with each other, form an integral organ, which, not being a closed system, continuously exchanges matter and energy with the environment. Such complex distributed active media with the presence of energy dissipation are characterized by self-organization processes. Due to the cumulative, cooperative action of a large number of objects in such systems, they are able to form various permanent or temporary spatial structures (Loskutov & Mikhailov, 2007). In the brain processes of self-organization (morphogenesis) also occurs when large populations of neurons form structures that function quite independently.
In addition to self-organization processes self-oscillations (fluctuations) often occur in such complex distributed systems. Despite the fact that the nature of these systems may be different and their constituent elements may be quite complex, this complexity does not manifest itself at the macro level. There are many examples of physical and chemical systems in which fluctuations, which play a fundamental role, arise as a result of self-organization processes. An example of such self-oscillations in complex biological systems can be fluctuations in the number of individuals in animal populations, periodic processes of photosynthesis, and many others (Haken, 2004).
The causes of fluctuations in complex distributed systems can be both external and internal endogenous factors. Self-oscillatory processes in the brain, the source of which are huge populations of neurons, are expressed at the macroscopic level in the rhythmic electrical activity of the brain, which can be recorded using an electroencephalographic device in various frequency ranges.
When considering complex systems, the chaos model is often used as the main model. Recently, the issues of modeling real chaotic systems have been given great importance. The choice of parameters for a model of a chaotic system is a rather difficult task, since such systems are very sensitive both to initial conditions and to small changes in parameters. To estimate the parameters of chaotic systems, optimization methods are currently widely used, including those based on genetic algorithms, particle swarm optimization, evolutionary algorithms, etc. (Volos et al., 2020). The main parameters characterizing chaotic systems are the average rate of information generation by a random data source (entropy) and the Lyapunov exponents (Pincus, 1991).
Entropy approach in methods of biomedical data analysis
Entropy as a measure of chaos is the most important universal concept that characterizes complex systems of various nature. The value of entropy gives an idea of how far the system is from a structured state and close to completely chaotic. Entropy is a very informative parameter that quantitatively characterizes the state of the system and is, on the one hand, a measure of the system's randomness, and, on the other hand, a measure of the missing information about the system. That is why entropy methods can be used to analyze data generated by a wide variety of natural and man-made systems, regardless of their origin. The evolution of the concept of entropy today covers at least several dozen generalizations of entropies. Entropy methods are widely used in various fields of science and technology, such as encryption, machine learning, natural language processing, and many others. In the technique of natural data analysis, an important place is occupied by methods based on the calculation of entropies by K. Shannon, A. Kolmogorov and A. Renyi (Chumak, 2011; dos Santos & Milidiú, 2012; Tian et al., 2011).
Shannon entropy
Information theory gives us the following definition of entropy, as a measure of system uncertainty proposed by Shannon (Shannon & Weaver, 1948):
, (1)
where {Pi} – probabilities for the system to be in states {i}.
Kolmogorov entropy
In the theory of dynamical systems, Kolmogorov generalized the concept of entropy to ergodic random processes through the limiting probability distribution having density f(x) (Chumak, 2011). Ergodic theory makes an attempt to explain the macroscopic characteristics of physical systems in terms of the behavior of the microscopic structure of the system (Martin & England, 1984). The Kolmogorov entropy is the most important characteristic of a chaotic system in a phase space of arbitrary dimension, showing the degree of chaoticity of a dynamic system. It can be defined as follows (Chumak, 2011; Schuster, 1988): let there be some stationary random process X(t) = [x1(t), x2(t), … xd(t)] on a strange attractor in a d-dimensional phase space. Consider some implementation of a random process, which is a temporal sequence of system states. We also define some finite sample (trajectory) i of the dynamical system from the given implementation. Let us divide the d-dimensional phase space of the system into cells of ld size. We will determine the state of the system at equal time intervals τ. Let us denote the joint probability so that X(t=0) is in i0 cell, X(t=τ) is in i1 cell , … , X(t=nτ) is in in cell. Then, according to Shannon, the quantity
, (2)
which is a measure of the a priori uncertainty of the position of the system is proportional to the information required to obtain the position of the system on a given trajectory with an accuracy of l, if only is known a priori. Therefore, Kn+1-Kn is the amount of loss of information about the system in the time interval from n to n+1. Thus, the Kolmogorov entropy is the average rate of information loss over time:
. (3)
For regular motion K=0, for random systems K=∞, for systems with deterministic chaos K is positive and constant (Schuster, 1988).
Algorithms for calculating sample and approximate entropy for physiological data
Equation (3) implies limiting values for temporal and spatial partitions and an infinite length of the time series under study. This limits the use of the Kolmogorov entropy by analytical systems and makes it difficult to use it for short and noisy time series of real measurements. To calculate the entropy of such time series, special robust methods were developed, based, for example, on the concept of approximate entropy and elementary sample entropy (sample entropy). These methods can significantly reduce the dependence of the calculation result on the sample length (Pincus, 1991; Richman & Moorman, 2000).
Approximate entropy and sample entropy are two statistics that make it possible to evaluate the randomness of a time series without having any prior knowledge of the data source (Delgado-Bonal & Marshak, 2019). Sample entropy (sampEn) is a method for estimating the entropy of a system that can be applied to short and noisy time series. The sample entropy gives a more accurate entropy estimate (Richman & Moorman, 2000) than the approximate entropy (Approximate entropy, apEn) introduced by Pincus (Pincus, 1991; Pincus & Goldberger, 1994).
Data used in the experiment
The data source was an open dataset of EEG clinical records at Temple University Hospital (TUH), Philadelphia, USA. This dataset is the largest publicly available dataset specifically designed to support research related to the development of machine learning algorithms for automated analysis of electroencephalogram recordings. The kit is focused on research on the detection of pathologies associated with epilepsy. The data in this set is manually labeled by neurologists using special labels. Due to the fact that the set contains real records of clinical studies, the composition of events in this set is diverse and complex. It contains, among other things, various epileptic events, a variant of the norm, as well as recording artifacts. Artifacts of the EEG recording are any extraneous events, the source of which is not the brain. Artifacts greatly complicate EEG analysis, both manual and automatic, and can serve as a source of false positives for machine learning algorithms.
Entropy calculation method used in the experiment
For the calculation, the SampEn sample entropy algorithm was chosen, as it gives the highest accuracy for noisy and short time series, such as EEG recordings. The calculations were carried out using a software module developed in the Python language using the nolds library, which implements the calculation of the nonlinear characteristics of dynamic systems for one-dimensional time series.
Experiment progress
- An EEG record of a patient suffering from epilepsy with the presence of areas of the record marked as pathological and areas corresponding to the norm was selected.
- The original signal was divided into non-overlapping windows of a fixed size, for each of which the sample entropy SampEn was calculated. Non-overlapping windows 2000 samples wide were used for calculations. Since the sampling frequency of the studied EEG records is 250 Hz, the window width corresponded to 8 sec. records. Calculations were carried out for all 22 channels (leads).
- The event label was set as the window label by the last value, i.e., if the last value in the window was marked as normal, then the entire window was marked as normal, and, accordingly, if the last value in the window was related to the pathological area, then the entire window was marked as pathological.
- The sample entropy value was calculated for each window. The calculation was carried out for each of the 22 leads.
- The calculation results were averaged for each of the events (normal, pathology) for all leads separately.
- Then, the average value of the sample entropy was obtained for all leads for areas corresponding to the norm and pathology.
Findings
Figure 1 shows the results of calculating the sample entropy SampEn for each of the 22 leads of the studied EEG recording.
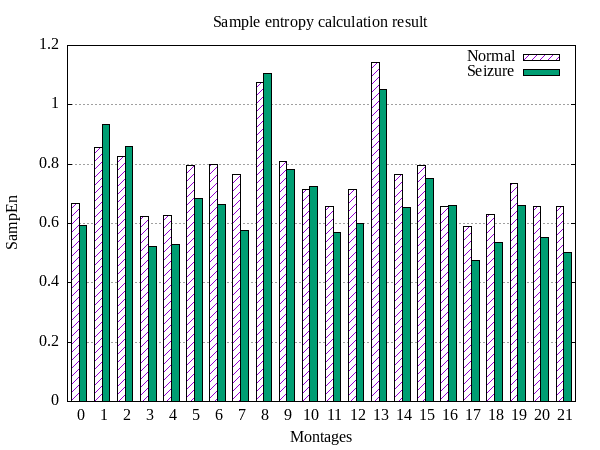
Figure 1 shows that for the majority of leads (17 out of 22 leads), the average value of the sample entropy for windows corresponding to pathology (generalized epileptic seizure) is lower than for windows marked as normal. This gives grounds for the conclusion that the entropy values for areas of "normal" EEG recording are higher than for areas corresponding to an epileptic seizure. This fact suggests that during an epileptic seizure, large populations of neurons are involved in the mode of pathological synchronization, while the dynamic complexity of the EEG signal decreases, which means that the value of entropy also decreases.
Conclusion
Differences between the average values of the sample entropy for the recording areas corresponding to the norm and pathological areas corresponding to a generalized epileptic seizure suggest the possibility of using the sample entropy as an informative feature in algorithms for automatic analysis of EEG data to detect pathologies associated with epilepsy.
Acknowledgments
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No.075-15-2022-1121).
References
Chumak, O. V. (2011). Entropy and fractals in data analysis. M.-Izhevsk: Research Center "Regular and Chaotic Dynamics". Institute for Computer Research.
Delgado-Bonal, A., & Marshak, A. (2019). Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy, 21(6), 541.
dos Santos, C. N., & Milidiú, R. L. (2012). Entropy Guided Transformation Learning: Algorithms and Applications. Springer.
Fergus, P., Hignett, D., Abir, H., Al-Jumeily, D., & Abdel-Aziz, K. (2015). Automatic Epileptic Seizure Detection Using Scalp EEG and Advanced Artificial Intelligence Techniques. BioMed Research International, 986736,
Goodfellow, Y., Bengio, I., & Courville, A. (2018). G93 Deep learning. DMK Press.
Haken, H. (2004). Synergetics: Introduction and Advanced Topics. Springer.
Kazakovtsev, L., Rozhnov, I., Popov, A., & Tovbis, E. (2020). Self-Adjusting Variable Neighborhood Search Algorithm for Near-Optimal k-Means Clustering. Computation 8(4), 90.
Loskutov, A. Y., & Mikhailov, A. (2007). Fundamentals of the theory of complex systems. M.-Izhevsk: Research Center "Regular and Chaotic Dynamics", Institute of Computer Science.
Martin, N., & England, J. (1984). Mathematical Theory of Entropy (Encyclopedia of Mathematics and its Applications). Cambridge University Press.
Obeid, I., & Picone, J. (2018). The Temple University Hospital EEG Data Corpus. In Augmentation of Brain Function: Facts, Fiction and Controversy. Volume I: Brain-Machine Interfaces. Lausanne. Frontiers Media S.A.
Peters, E. (2000). Chaos and order in capital markets. A new analytical look at cycles, prices and market volatility. Mir.
Pincus, S. M. (1991). Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences, 88, 2297–2301.
Pincus, S. M., & Goldberger, A. L. (1994). Physiological time-series analysis: what does regularity quantify? American Journal of Physiology-Heart and Circulatory Physiology, 266(4), 1643–1656.
Richman, J. S., & Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology, 278(6), 2039–2049. https://doi.org/
Schuster, H. G. (1988). Deterministic chaos: Introduction. Mir.
Shah, V., von Weltin, E., Lopez, S., McHugh, J., Veloso, L., Golmohammadi, M., Obeid, I., & Picone, J. (2018). The Temple University Hospital Seizure Detection Corpus. Frontiers in Neuroinformatics. 12, 83.
Shannon, C. E., & Weaver, W. (1948). The mathematical theory of communication. University of Illinois Press.
Tian, X., Le, T. M., & Lian, Y. (2011). Review of CAVLC, Arithmetic Coding, and CABAC. Entropy Coders of the H.264/AVC Standard (pp. 29-39). Springer.
Volos, C. K., Jafari, S., Munoz-Pacheco, J. M., Kengne, J., & Rajagopal, K. (2020). Nonlinear Dynamics and Entropy of Complex Systems with Hidden and Self-Excited Attractors II. Entropy, 22(12), 1428.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Egorova, L. (2023). Entropy Approach in Methods of Electroencephalogram Automatic Analysis. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 275-282). European Publisher. https://doi.org/10.15405/epct.23021.34

