Approach to Data Clustering Based on Molecular Chemical Reactions With Various Distance Measures

Abstract

Automatic clustering involves dividing a set of objects into subsets so that the objects from one subset are more similar to each other than to the objects from other subsets according to some criterion. The paper proposes an algorithm for clustering data using the k-means algorithm combined with molecular chemical reactions and with various types of distance measures: Euclidean distance, Squared Euclidean distance, Manhattan distance. This approach mimics a chemical reaction process in which reactants interact with one another. Every chemical reaction process generate a new molecular structure in the environment. By molecular structure, we mean a possible solution to data clustering, by optimizing the molecular chemical reactions we mean optimizing the results of data clustering (search for a global optimal solution). The solution obtained with k-means is used as an initial molecular structure solution to optimize chemical reactions by generating new solutions: single-molecule collision, single-molecule decomposition, intermolecular collision, and intermolecular synthesis. Computational experiments demonstrate the comparative efficiency and accuracy of using the k-means algorithm combined with molecular chemical reactions.

Keywords: Data clustering, chemical reaction optimization, k-means

Introduction

One of the most well-known automatic grouping models is the k-means model (1) (Hossain et al., 2019; Li & Wu, 2012), which was proposed by Steinhaus (1956).

$\text{argmin}F(X_1,\text{...},X_k)=\sum \underset{j\in \overline{\left\{1,k\right\}}}{\text{min}}{‖X_j-A_i‖}^2$ (1)

The goal of the k-means problem is to find points (centers, centroids)₁,..., in a d-dimensional space such that the sum of the squared distances from the known points₁,..., to the nearest of the desired points reaches a minimum. Lloyd (1982) algorithmically implemented the k-means problem. In the works MacQueen (1967), the basic k-means algorithm, also known as Lloyd's algorithm, consists of iterative repetition of two steps:

• Given: k initial cluster centers (centroids).

Step 1. Create a new cluster Cj $(j=\stackrel{-}{\mathrm{1},k)}$ by assigning each data point to the closest cluster center (centroid).

Step 2. Calculation of new cluster centers.

Repeat steps 1 and 2 until there are no more changes within each cluster.

In the k-means algorithm, it is necessary to initially predict the number of groups (subsets). In addition, the result obtained depends on the initial choice of centers.

Kaufman and Rousseeuw (1987) presented the k-medoids model (PAM, Partitioning Around Medoids) close to k-means. The centers are clustered objects (medoids) that are part of the set under study. The algorithm is more resistant to outliers and noise than the k-means algorithm; however, it is inefficient when applied to large datasets due to time complexity. The k-medians algorithm (Jain & Dubes, 1988) is a variation of the k-means algorithm, where the median is calculated instead of the mean to determine the cluster centroid. Kaufman and Rousseeuw (1990) proposed the CLARA (Clustering Large Applications) algorithm, based on the PAM algorithm, for clustering objects in large databases in order to reduce computation time. In (Ng & Han, 2002) the authors propose the CLARANS (Clustering Large Applications based upon Randomized Search) algorithm, which is aimed at using a randomized search to facilitate the clustering of a large number of objects.

Algorithms k-means, k-medians, k-medoid, PAM, CLARA, CLARANS belong to the class of clustering algorithms based on partitioning methods (Partitioning clustering).

The current literature offers many heuristic approaches (Arthur & Vassilvitskii, 2007) to setting the initial centroids for the k-means algorithm, which are basically various evolutionary and random search methods. Local search algorithms and randomized algorithms based on them are presented in a large number of publications. For example, Variable Neighborhood Search (VNS) algorithms (Mladenović & Hansen, 1997; Rozhnov et al., 2019) or agglomeration algorithms (Sun et al., 2014) sometimes perform well. Initialization procedures for local search algorithms are also widely presented, including random filling and estimation of the distribution of demand points (Arthur & Vassilvitskii, 2007). However, in many cases, even repeated runs of simple local search algorithms from various randomly generated solutions do not provide a solution to the problem close to the global optimum. More complex algorithms make it possible to obtain the values of the objective function (1) many times better than local search methods (Rozhnov et al., 2019).

A popular idea is to use genetic algorithms and other evolutionary approaches to improve local search results (Krishna & Murty, 1999; Maulik & Bandyopadhyay, 2000). Such algorithms combine local minima obtained using the k-means algorithm. Heretic algorithms operate on a certain set (population) of candidate solutions and include special genetic operators (algorithms) for initialization of selection, crossover, and mutation. The mutation operator randomly changes the resulting solutions and provides some diversity in the population. However, in such algorithms, as the number of iterations increases, the population degenerates into a certain set of solutions that are close to each other. Larger populations as well as dynamically growing populations improve this situation.

Classical clustering algorithms, such as k-means, perform a local search, improving the previous result. The result of the algorithm depends on the initial solution chosen. Therefore, the search for the optimal solution requires multiple attempts to run algorithms with procedures for random selection of initial solutions or random selection of local search (Vidyasagar, 1998), or the use of these procedures in the algorithm simultaneously. More complex algorithms can be applied, such as genetic algorithms, neural networks (Holland, 1975), simulated annealing algorithm (Kirkpatrick et al., 1983). These algorithms are based on the idea of modeling natural processes. The authors of the paper “Genetic K-Means algorithm” (Krishna & Murty, 1999) showed the advantage of genetic algorithms over classical algorithms. The genetic algorithm is a representative of evolutionary optimization algorithms (search for the optimal solution).

In his work, J. Holland introduces the concept of a fitness function (Holland, 1975), which is intended to determine the best solution for a genetic algorithm. The fitness function is the objective function. The purpose of crossing genes is to achieve the best value of the objective function.

The genetic algorithm for solving the discrete p-median problem proposed by Hosage and Goodchild (1986) preceded the genetic algorithm for the k-means problem. The authors of (Bozkaya et al., 2002) presented a genetic algorithm with solution coding in the form of a set of indices of network nodes chosen as a center using several crossing operators. The algorithm gave more accurate results with very slow convergence. In their work, Alp et al. (2003) presented a simple and faster genetic algorithm with a special crossing procedure - a greedy (agglomerative) heuristic procedure, which also gives exact results for the p-median network problem. This idea was inherited in (Kazakovtsev & Antamoshkin, 2014). Many mutation methods presented in (Kazakovtsev & Antamoshkin, 2014; Kwedlo & Iwanowicz, 2010) can be used in genetic algorithms for k-means and similar problems. In the k-means algorithm, usually the initial solution is a subset of the original data. In (He & Yu, 2019), the authors solve an alternative k-means problem aimed at increasing the stability of clustering instead of minimizing (1). The authors of (Pizzuti & Procopio, 2017) solve the problem with a mathematical formulation different from (1) and use cluster recalculation in accordance with (1) as a mutation operator. A similar coding is used in (Krishna & Murty, 1999), where the authors propose a mutation operator that changes the assignment of individual data objects to clusters. In the mutation operator is described as a procedure that guarantees the diversity of a population (Eremeev, 2012). For the k-means and p-median problem, the mutation procedure, as a rule, changes one or more solutions, replacing some centers (Krishna & Murty, 1999; Maulik & Bandyopadhyay, 2000).

Different mutation operators have been developed for different decision encoding methods: bit inversion for binary encoding (Holland, 1975), swap, insertion, inversion, and bias permutation (Larranaga et al., 1999) for variable length solutions, Gaussian mutation (Sarangi et al., 2015) and polynomial mutation for real encoding (Deb & Deb, 2012). Some studies propose a combination of mutation operators (Deep & Mebrahtu, 2011) or self-adaptive mutation operators (McGinley et al., 2011). The efficiency of various mutation operators depends on the parameters of the genetic algorithm (Osaba et al., 2014) and the type of problem (Karthikeyan et al., 2013). In Krishna and Murty (1999), Cheng et al. (2006), the authors propose to use the k-means algorithm as a mutation operator. Each of these algorithms declares a local search as a mutation operator. The structure of the genetic algorithm allows us to use a wide range of variants of genetic operators. However, local search is intended to improve an arbitrary solution by transforming it into a local optimum and thereby reducing rather than increasing the diversity of solutions.

Problem Statement

The problem of automatic classification (the problem of automatic clustering) can be described as follows. objects of a certain set must be divided into non-overlapping subsets so that the objects of one subset have similar features with each other and do not have them with objects from other subsets. The result clustering depends on the initially selected number of subsets and the measure of similarity (difference), expressed as a function of distances.

In Jain and Dubes (1988), the following formulation of the cluster analysis problem is proposed: let there be a sample of research objects={₁,...,}, where is the sample size. It is required to form≥2 classes (groups of objects). The number of classes can be preselected or determined automatically. Each object is described using a set of variables₁,...,. The set={₁,...,} can include variables of different types.

Research Questions

The search for an object clustering algorithm that has both high accuracy and stability of the result, and at the same time high speed, is one of the problems of automatic grouping of objects. The presented work is devoted to the research and development of a new algorithm for automatic grouping of objects, which will improve the accuracy and stability of the result of solving practical problems.

Purpose of the Study

The purpose of the study of this work is to improve the accuracy and stability of the result of solving problems of automatic grouping of objects.

Research Methods

In this paper, we propose an algorithm similar to the genetic algorithm, in which molecular chemical reactions are used as the mutation procedure (KCR algorithm). This approach mimics a chemical reaction process in which reactants interact with one another. Every chemical reaction process generate a new molecular structure in the environment (Pan et al., 2015). By molecular structure, we mean a possible solution to data clustering, by optimizing the molecular chemical reactions we mean optimizing the results of data clustering (search for a global optimal solution).

Imagine a possible solution to clustering as a molecular structure. Let each molecule consist of two sets of atoms. The first set of atoms contains a sequence of point numbers A = {A1, A2, … , AN}, the second set contains the numbers of clusters from X={X1, X2, ... , Xk} to which the corresponding points belong. Figure 1 shows an example of a possible molecular structure that contains three clusters and eight points.

See Full Size >

Generation of new clustering solutions

The paper proposes to consider and apply four types of chemical reactions: single- molecule collision, single-molecule decomposition, intermolecular collision and intermolecular synthesis (McNaught & Wilkinson, 1997).

Single molecule collision

In one substitution reaction, one element replaces another in a compound. The new molecular structure Φ' is obtained as follows. In the initial molecular structure, we randomly select a point and change its membership in the={} cluster randomly (Figure 2).

See Full Size >

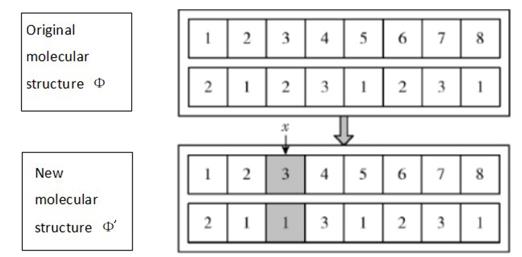
Single molecule decomposition

A decomposition reaction is an approach where a more complex substance breaks down into simpler parts. In the clustering problem, two new molecular structures Φ1' and Φ2' are generated from the initial molecular structure (Figure 3). The new molecular structure Φ1' is obtained as follows. Points with uneven numbers and their corresponding cluster numbers are stored in the new molecular structure, and for points with even numbers, we determine their belonging to a cluster of={₁,₂, ... ,_k} randomly. The new molecular structure Φ2' is obtained as follows. Points with even numbers and the corresponding cluster numbers are stored in the new molecular structure, and for points with uneven numbers, we determine their belonging to a cluster of={₁,₂, ... ,_k} randomly.

See Full Size >

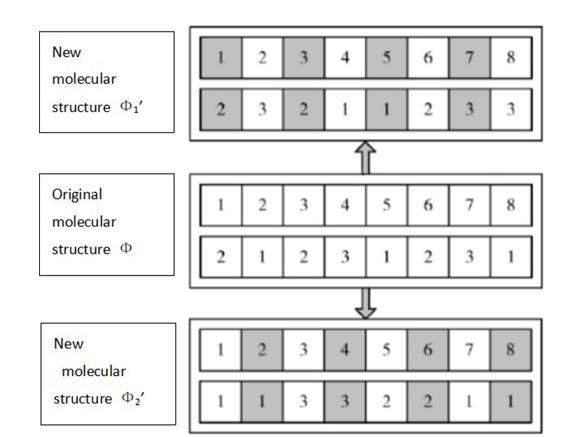
Intermolecular collision

In intermolecular collisions, the anions and cations of two compounds switch places and form two entirely different compounds. New molecular structures Φ1' и Φ2' is obtained as follows. The numbers of two pointsand(<) are randomly chosen in two initial molecular structures Φ1 and Φ2. The new molecular structure Φ1' is obtained by copying the initial molecular structure Φ2. Then we replace the cluster numbers for theth points ( [,]) from the molecular structure Φ1. The new molecular structure Φ2' is obtained by copying the initial molecular structure Φ1. Then we replace the cluster numbers for theth points ( [,]) from the molecular structure Φ2 (Figure 4).

See Full Size >

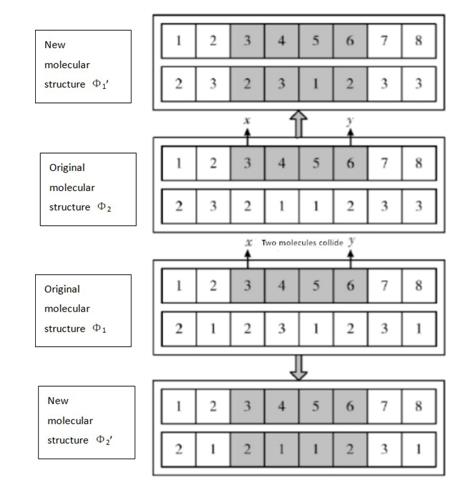
Intermolecular synthesis

In a synthesis reaction, two or more simple substances combine to form a more complex substance. The number of pointis randomly chosen in two initial molecular structures Φ1 and Φ2. The new molecular structure Φ' is obtained by copying the initial molecular structure Φ1. Then we replace the cluster numbers for theth points (i  [+1,]) from the molecular structure Φ2 (Figure 5).

See Full Size >

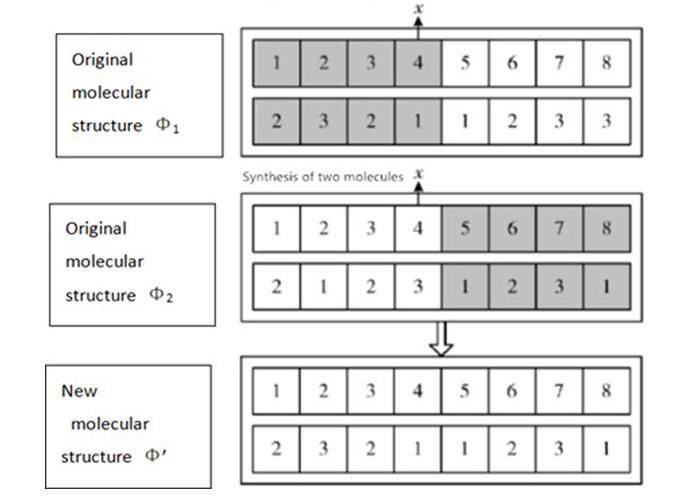
For each new solution (new molecular structure), we calculate the value of the objective function. If the objective function value of the new solution is better than the objective function value of the initial solution, then the new molecular structure is a valid solution (see Algorithm 1). In our work, the value of the objective function is defined as (1). The distance measures used are described below.

The Minkowski function (Kulin & Kuenne, 1962):

$d\left(x,y\right)={\left({\sum }_{i=\mathrm{1}}^M{\left|x_i-y_i\right|}^p\right)}^{\frac{\mathrm{1}}{p}}$ (2)

where and are input vectors of dimension. For parameter, the following statement ate true (proof): for 1 and = the distance is a metric; for < 1 the distance is not a metric.

The Euclidean distance (EuD). For = 2, the function (2) the takes the form of Euclidean distance:

$d\left(x,y\right)=\sqrt{{\sum }_{i=1}^M{\left(x_i-y_i\right)}^2}$ (3)

The squared Euclidean distance (SEuD):

$d\left(x,y\right)=\sqrt{{\sum }_{i=\mathrm{1}}^M{\left(x_i-y_i\right)}^{\mathrm{2}}}$

(4)

The Manhattan distance (ManD). For = 1, we get (2) the Manhattan distance, which is the second most popular distance:

$d\left(x,y\right)=\sqrt{{\sum }_{i=\mathrm{1}}^M\left|x_i-y_i\right|}$ (5)

Findings

In this section, we compare the results of the experiment performed with k-means and KCR algorithms with various types of distance measures: Euclidean distance, Squared Euclidean distance, Manhattan distance.

For the experiments, we used Synthetic (artificial) datasets (with cluster labels) (GitHub Inc. [GHI], 2022), as well as from samples of industrial products (Kazakovtsev et al., 2015; Shkaberina et al., 2020).

• Square3 is artificial dataset contains the collection of four clusters (1000 data points, 2 dimensions).
• Microchips 1526IE10_002 set of results of test effects on electrical and radio products for monitoring the current-voltage characteristics of input and output circuits of microcircuits (3987 data points, 67 dimensions).

Algorithms were implemented in Python. For the computational experiments, we used the following test system: AMD Ryzen 5 3500U, 2.10 GHz, 8 CB RAM.

For various datasets, the minimum (min), maximum (max), mean (mean), standard deviation (σ), coefficient of variation (V) and the the span factor (R) of the objective function are calculated (Tables 1,2). In the tables, the best mean values of objective function are given in bold.

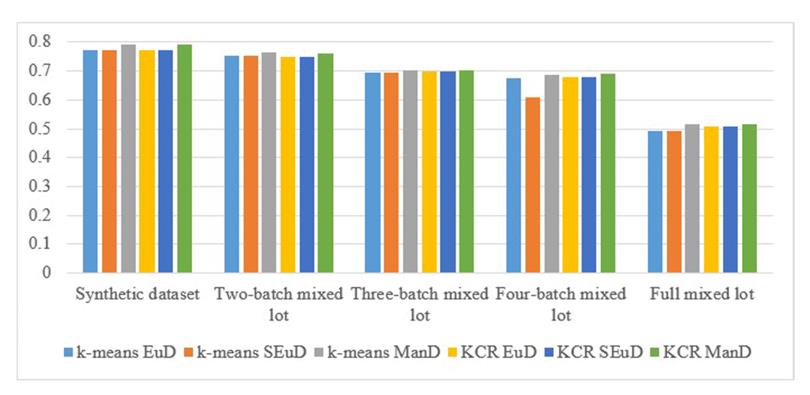
Computational experiments showed that in the vast majority of cases, minimal mean objective function value was demonstrated by KCR algorithm with Euclidean distance. However, using the KCR algorithm with Manhattan distance, in most cases, improves the accuracy of data clustering (Figure 6). In addition, the clustering accuracy increases with increasing number of points in the dataset (Table 3).

See Full Size >

Conclusion

We proposed KCR algorithm for data clustering, which combines k-means algorithm and chemical reaction algorithms, could achieve an effective balance between local search capabilities and global exploration capabilities. The new algorithm improves the accuracy of solving the k-means problem.

Computational experiments showed that in the vast majority of cases, minimal mean objective function value was demonstrated by KCR algorithm with Euclidean distance. However, using the KCR algorithm with Manhattan distance, in most cases, improves the accuracy of data clustering. In addition, the clustering accuracy increases with increasing number of points in the dataset.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No.075-15-2022-1121).

References

• Alp, O., Erkut, E., & Drezner, Z. (2003). An Efficient Genetic Algorithm for the p-Median Problem. Annals of Operations Research, 122(1-4), 21-42. DOI: 10.1023/A:1026130003508

• Arthur, D., & Vassilvitskii, S. (2007). K-Means++: The Advantages of Careful Seeding. Proceedings of SODA’07, SIAM, 1027-1035.

• Bozkaya, B. A., Zhang, J., & Erkut, E. (2002). Genetic Algorithm for the p-Median Problem. Facility Location: Applications and Theory (pp. 179-205). Springer. DOI:

  Google Scholar

  Crossref

• Cheng, S. S., Chao, Y. H., Wang, H. M., & Fu, H. C. (2006). A prototypes-embedded genetic k-means algorithm. In 18th International Conference on Pattern Recognition (ICPR'06) (Vol. 2, pp. 724-727). IEEE. DOI:

  Google Scholar

  Crossref

• Deb, D., & Deb, K. (2012). Investigation of mutation schemes in real-parameter genetic algorithms. In Swarm, Evolutionary, and Memetic Computing: Third International Conference, SEMCCO 2012, Bhubaneswar, India, December 20-22, 2012. Proceedings 3 (pp. 1-8). Springer. DOI:

  Google Scholar

  Crossref

• Deep, K., & Mebrahtu, H. (2011). Combined mutation operators of genetic algorithm for the travelling salesman problem. International Journal of Combinatorial Optimization Problems and Informatics, 2(3), 1-23. https://www.redalyc.org/pdf/2652/265219635002.pdf

• Eremeev, A. V. (2012). A genetic algorithm with tournament selection as a local search method. Journal of Applied and Industrial Mathematics, 6(3), 286-294. DOI:

  Google Scholar

  Crossref

• GitHub Inc. (2022, November 18). Artificial Clustering Datasets. https://github.com/milaan9/Clustering-Datasets (accessed on 14 October 2022).

• He, Z., & Yu, C. (2019). Clustering stability-based Evolutionary K-Means. Soft Computing, 23(1), 305-321. DOI:

  Google Scholar

  Crossref

• Holland, J. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press.

• Hosage, C. M., & Goodchild, M. F. (1986). Discrete Space Location-Allocation Solutions from Genetic Algorithms. Annals of Operations Research, 6, 35-46. DOI:

  Google Scholar

  Crossref

• Hossain, M. Z., Akhtar, M. N., Ahmad, R. B., & Rahman, M. (2019). A dynamic K-means clustering for data mining. Indonesian Journal of Electrical Engineering and Computer Science, 13(2), 521. DOI:

  Google Scholar

  Crossref

• Jain, A. K., & Dubes, R. C. (1988). Algorithms for Clustering Data. Prentice-Hall.

• Karthikeyan, P., Baskar, S., & Alphones, A. (2013). Improved genetic algorithm using different genetic operator combinations (GOCs) for multicast routing in ad hoc networks. Soft Computing, 17, 1563-1572. DOI:

  Google Scholar

  Crossref

• Kaufman, L., & Rousseeuw, P. J. (1987). Clustering by means of medoids. In Proc. Statistical Data Analysis Based on the L1 Norm Conference (pp. 405-416). Springer.

• Kaufman, L., & Rousseeuw, P. J. (1990). Finding groups in data: an introduction to cluster analysis. Wiley.

• Kazakovtsev, L. A., & Antamoshkin, A. N. (2014). Genetic Algorithm with Fast Greedy Heuristic for Clustering and Location Problems. Informatica, 38(3), 229-240.

• Kazakovtsev, L. A., Antamoshkin, A. N., & Masich, I. S. (2015). Fast deterministic algorithm for EEE components classification. 2015 IOP Conference Series: Materials Science and Engineering, 94, 012015. DOI:

  Google Scholar

  Crossref

• Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671-680. DOI:

  Google Scholar

  Crossref

• Krishna, K., & Murty, M. M. (1999). Genetic K-Means algorithm. IEEE Transactions on Systems. Part B (Cybernetics), 29(3), 433-439. DOI:

  Google Scholar

  Crossref

• Kulin, H. W., & Kuenne, R. E. (1962). An efficient algorithm for the numerical solution of the generalized Weber problem in spatial economics. Journal of Regional Science, 4(2), 21-33.

• Kwedlo, W., & Iwanowicz, P. (2010). Using Genetic Algorithm for Selection of Initial Cluster Centers for the K-Means Method. ICAISC 2010: Artificial Intelligence and Soft Computing, 165-172. DOI:

  Google Scholar

  Crossref

• Larranaga, P., Kuijpers, C. M. H., Murga, R. H., Inza, I., & Dizdarevic, S. (1999). Genetic algorithms for the travelling salesman problem: A review of representations and operators. Artificial intelligence review, 13, 129-170. DOI:

  Google Scholar

  Crossref

• Li, Y., & Wu, H. (2012). A Clustering Method Based on K-Means Algorithm. Physics Procedia, 25, 1104-1109. DOI:

  Google Scholar

  Crossref

• Lloyd, S. P. (1982). Least Squares Quantization in PCM. IEEE Transactions on Information Theory, 28, 129-137. DOI:

  Google Scholar

  Crossref

• MacQueen, J. B. (1967). Some Methods of Classification and Analysis of Multivariate Observations. Proceedings of the 5th Berkley Symposium on Mathematical Statistics and Probability, 1, 281-297.

• Maulik, U., & Bandyopadhyay, S. (2000). Genetic Algorithm-Based Clustering Technique. Pattern Recognition, 33(9), 1455-1465. DOI:

  Google Scholar

  Crossref

• McGinley, B., Maher, J., O'Riordan, C., & Morgan, F. (2011). Maintaining healthy population diversity using adaptive crossover, mutation, and selection. IEEE Transactions on Evolutionary Computation, 15(5), 692-714. DOI:

  Google Scholar

  Crossref

• McNaught, A. D., & Wilkinson, A. (1997). Compendium of Chemical Terminology (2nd ed., the "Gold Book"). Blackwell Scientific Publications.

• Mladenović, N., & Hansen, P. (1997). Variable neighborhood search. Computers & operations research, 24(11), 1097-1100. DOI:

  Google Scholar

  Crossref

• Ng, R. T., & Han, J. (2002). CLARANS: a method for clustering objects for spatial data mining. IEEE Transactions on Knowledge and Data Engineering, 14(5), 1003-1016. DOI:

  Google Scholar

  Crossref

• Osaba, E., Carballedo, R., Diaz, F., Onieva, E., de la Iglesia, I., & Perallos, A. (2014). Crossover versus Mutation: A Comparative Analysis of the Evolutionary Strategy of Genetic Algorithms Applied to Combinatorial Optimization Problems. The Scientific World Journal, 1-22. DOI:

  Google Scholar

  Crossref

• Pan, G., Xu, Y., Ouyang, A., & Zheng, G. (2015). An Improved Artificial Chemical Reaction Optimization Algorithm for Job Scheduling Problem in Grid Computing Environments. Journal of Computational and Theoretical Nanoscience, 12(7), 1300-1310. DOI:

  Google Scholar

  Crossref

• Pizzuti, C., & Procopio, N. (2017). A K-means based genetic algorithm for data clustering. In International Joint Conference SOCO’16-CISIS’16-ICEUTE’16: San Sebastián, Spain, October 19th-21st, 2016 Proceedings 11 (pp. 211-222). Springer, Cham. DOI:

  Google Scholar

  Crossref

• Rozhnov, I. P., Orlov, V. I., & Kazakovtsev, L. A. (2019). VNS-Based Algorithms for the Centroid-Based Clustering Problem. Facta Universitatis Series: Mathematics and Informatics, 34(5), 957-972. DOI:

  Google Scholar

  Crossref

• Sarangi, A., Lenka, R., & Sarangi, S. K. (2015). Design of linear phase FIR high pass filter using PSO with gaussian mutation. Swarm, Evolutionalry, and Memetic Computing, SEMCCO 2014, 8947, 471-479. DOI:

  Google Scholar

  Crossref

• Shkaberina, G. S., Orlov, V. I., Tovbis, E. M., & Kazakovtsev, L. A. (2020). On the Optimization Models for Automatic Grouping of Industrial Products by Homogeneous Production Batches. Communications in Computer and Information Science, 1275, 421-436. DOI:

  Google Scholar

  Crossref

• Steinhaus, H. (1956). Sur la divisiondes corps materiels en parties. Bulletin L'Académie Polonaise des Science, 3(4), 801-804.

• Sun, Z., Fox, G., Gu, W., & Li, Z. (2014). A parallel clustering method combined information bottleneck theory and centroid-based clustering. The Journal of Supercomputing, 69, 452-467. DOI:

  Google Scholar

  Crossref

• Vidyasagar, M. (1998). Statistical learning theory and randomized algorithms for control. IEEE Control Systems, 12, 69-85. DOI:

  Google Scholar

  Crossref