Multi-Swarm PSO With Success-History Based Adaptive Local Search for Dynamic Environments

Abstract

In this paper, a success-history based parameter adaptation is proposed for the local search procedure used in particle swarm optimization algorithm with multiple swarms. The proposed modified version of the mQSO algorithm is considered within the generalized moving peaks dynamic optimization benchmark set. For the experiments, a set of 12 benchmark problems are chosen from the CEC 2022 competition on dynamic optimization. The experiments involving parameter sensitivity analysis have shown that the adaptive local search with particles generated next to the global best of each swarm with normal distribution allows improving the overall performance of the algorithm in terms of current error and best error before each environment change. An additional set of experiments with increased shifts of peaks between environmental changes has been performed to test the influence of the initial settings of local search with quantum or normally distributed particles. The results have shown that applying adaptive sampling width for normal distribution allows improving performance in cases of bad choice of population size or number of local search particles on every iteration.

Keywords: Particle swarm optimization, dynamic optimization, local search, parameter adaptation

Introduction

The optimization problems in the real world can be classified into two main categories: static and dynamic problems. Dynamic optimization problems (DOPs) consider a more difficult case, when the problem itself may change over time while being solved. Examples of such problems are online control, online path planning, etc (Nguyen et al., 2012; Yazdani et al., 2021a). Depending on the task, DOPs differ in the frequency and severity of goal function changes, optima trajectory, number of base functions and homogeneity of optima movement (De Jong, 1999).

Although the simplest approach to dynamic optimization is restarting once an environmental change is detected, today the heuristic optimization algorithms are widely and successfully used for DOPs. In particular, evolutionary algorithms (EAs) and swarm intelligence (SI) methods, such as particle swarm optimization (PSO), have proved to be efficient for solving DOPs due to their natural adaptive properties. Several approaches have been proposed for EAs, such as hyper-mutation, memory schemes, and multi-population schemes (Nguyen, 2011). Nevertheless, the PSO-based algorithms have been more successful for DOPs due to their ability for fast convergence, for example the mQSO algorithm (Blackwell & Branke, 2006).

In this study, we focus on one of the aspects of applying PSO-based approaches for DOPs, indicated in a recent survey (Yazdani et al., 2021a). In particular, the automatic parameter tuning is rarely addressed in studies on dynamic optimization (Huang et al., 2020). One of the efficient tuning schemes for differential evolution is the success-history based parameter adaptation (SHA) proposed in (Tanabe & Fukunaga, 2013). In the current study SHA is applied to tuning the local search part of the mQSO algorithm, i.e. generating quantum points near the best solution of each swarm. The experiments are performed on the CEC 2022 benchmark DOPs, generated by generalized moving peaks benchmark (GMPB) (Yazdani et al., 2021b). The main contributions of this paper are the following:

• The population size and the number of quantum particles in mQSO significantly influence the overall performance, and the typical values are far from optimal for CEC 2022 DOPs benchmark;
• Modifying the local search by changing uniform distribution to normal distribution allows improving the performance of mQSO;
• Applying success-history based adaptation to tuning the local search parameters allows improving the performance of the search algorithm in some cases, especially if the shift of optima between environmental changes is large.

The rest of the paper is organized as follows: section 2 describes the mQSO algorithm and the benchmark suite, section 3 proposes the modifications, section 4 contains experimental setup and results, and section 5 concludes the paper.

Problem Statement

The dynamic optimization problem in general can be formulated as follows:

$optimize\mathrm{}f\left(\stackrel{-}{x},\stackrel{-}{\phi },t\right),\mathrm{}\stackrel{-}{x}\in F\left(t\right)\subseteq S,t\in T$,

where $S\in R^d$, $d$ is the dimensionality of the search space $S$, $t$ denotes the time, $\stackrel{-}{\phi }$ is the set of parameters of the current environment, $f:S\times T\to R$, is the objective function that returns a value $\left(f\left(\stackrel{-}{x},\stackrel{-}{\phi },t\right)\right)\in R$ using the feasible solution from the search space at time $t$, $F\left(t\right)$—is a set of feasible solutions at time $t$.

One of the recently proposed benchmarks for dynamic optimization is the Generalized Moving Peaks Benchmark (GMPB) (Yazdani et al., 2021b), which is capable of generating different types of dynamic problems based on a set of parameters. GMPB allows generating fully non-separable or fully separable problems, with homogeneous or heterogeneous sub-functions, multimodal, asymmetric and irregular components. The following baseline function is used in GMPB:

$f^{\left(t\right)}\left(x\right)=\underset{k\in \left\{\mathrm{1},\dots ,m\right\}}{\max }\left\{h_k^{\left(t\right)}-\sqrt{T\left({\left(x-c_k^{\left(t\right)}\right)}^T{R}_k^{\left(t\right)T},k\right)W_k^{\left(t\right)}T\left({R_k^{\left(t\right)}\left(x-c_k^{\left(t\right)}\right)}^T,k\right)}\right\}$,

$T\left(y_j,k\right)=\left\{\begin{array}{c}exp\left(log\left(y_j\right)+{\tau }_k^{\left(t\right)}\left(sin\left({\eta }_{k,\mathrm{1}}^{\left(t\right)}log\left(y_j\right)\right)+sin\left({\eta }_{k,\mathrm{2}}^{\left(t\right)}log\left(y_j\right)\right)\right)\right),\mathrm{}{y}_j>\mathrm{0}\\ \begin{array}{c}\mathrm{0},\mathrm{}{y}_j=\mathrm{0}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\\ -exp\left(log\left(\left|y_j\right|\right)+{\tau }_k^{\left(t\right)}\left(sin\left({\eta }_{k,\mathrm{3}}^{\left(t\right)}log\left(\left|y_j\right|\right)\right)+sin\left({\eta }_{k,\mathrm{4}}^{\left(t\right)}log\left(\left|y_j\right|\right)\right)\right)\right),\mathrm{}{y}_j>\mathrm{0}\end{array}\end{array}\right.j=\stackrel{-}{\mathrm{1},d}$

where $x$ is a solution vector, $d$ is the number of dimensions, is the number of components, $c_k^{\left(t\right)}$ is the vector of center positions of the $k$-th component at time $t$, $R_k^{\left(t\right)}$ is the rotational matrix of component $k$ in the environment $t$, $W_k^{\left(t\right)}$ is a width matrix (it is a $d\times d$ diagonal matrix where each diagonal element is the width of the component $k$), and, finally, ${\eta }_{k,l}^{\left(t\right)}$, $l=\stackrel{-}{\mathrm{1,4}}$ , and ${\tau }_k^{\left(t\right)}$ are the irregularity parameters of the component $k$. When an environmental change is triggered, the height, width, irregularity and other parameters are changed for every component.

Research Questions

The following questions are addressed in current study:

• What is the influence of the number of particles in the mQSO algorithm on the overall performance?
• What are the ways to improve the local search abilities of the mQSO algorithm?
• How the success-history based adaptation can be implemented for parameter tuning in mQSO algorithm?

Purpose of the Study

The purpose of this study is to improve the performance of the dynamic optimization algorithm mQSO using the success-history based parameter adaptation for quantum particles generation.

Research Methods

The multi-swarm Quantum Swarm Optimization is a well-known approach for DOPs, originally proposed in (Blackwell & Branke, 2006). mQSO follows the general scheme of PSO approach with particles and velocities, but uses several swarms and quantum particles for local search. The method starts by initializing a set of $N_s$ swarms of $N_p$ particles with positions $x_{nij}$, $n=\mathrm{1,2},\dots ,N_s$, $i=\mathrm{1,2},\dots ,N_p$, $j=\mathrm{1,2},\dots ,D$. The version of the algorithm considered here uses only neutral and quantum particles, but not charged, as described in (Yazdani et al., 2020). The velocities and positions are updated as follows:

$\stackrel{\to }{u_{ni}}\leftarrow w\left[\stackrel{\to }{u_{ni}}+c_{\mathrm{1}}\stackrel{\to }{{\epsilon }_{\mathrm{1}}}\odot \left(\stackrel{\to }{p_{ng}}-\stackrel{\to }{x_{ni}}\right)+c_{\mathrm{2}}\stackrel{\to }{{\epsilon }_{\mathrm{2}}}\odot \left(\stackrel{\to }{p_{ni}}-\stackrel{\to }{x_{ni}}\right)\right]$,

$\stackrel{\to }{x_{ni}}=\stackrel{\to }{x_{ni}}+\stackrel{\to }{u_{ni}}$

where $i=\mathrm{1,2},\dots ,N_p$ is the particle’s index in the population, $\stackrel{\to }{u_{ni}}$ is the velocity of $i$-th particle in $n$-th swarm, $n=\mathrm{1,2},\dots ,N_s$ , $\stackrel{\to }{x_{ni}}$ is current particle position, $\stackrel{\to }{p_{ni}}$ is the personal best position, $\stackrel{\to }{{\epsilon }_1}$ and $\stackrel{\to }{{\epsilon }_2}$ are random vectors in ${\left[\mathrm{0,1}\right]}^D$, $c_1$ and $c_2$ are social and cognitive parameters, $w$ is the inertia factor, $p_{ng}$— is the global best solution, $\odot$ denotes the element-wise product. The quantum particles are generated using uniform distribution around the global best solution with parameter $r_{cloud}$ for $N_q$ iterations: $\stackrel{\to }{x_q}\in \stackrel{\to }{p_{ng}}+U\left(-r_{cloud},r_{cloud}\right)$, as proposed in the code for the CEC 2022 benchmark.

The mQSO algorithm has two additional mechanisms, namely exclusion and anti-convergence. The exclusion mechanism is triggered every iteration after all swarms have moved. If the Euclidean distance $dist\left(\stackrel{\to }{p_{ng},}\stackrel{\to }{p_{mg}}\right)$ between $n$-th and $m$-th swarms’ best positions is less than $r_{excl}$ parameter, then the worst swarm is reinitialized. The anti-convergence mechanism is executed after exclusion, and checks if any of the swarms have converged by calculating $\left|S_n\right|={max}_{kl}{max}_j\left|\left(\stackrel{\to }{x_{nk}}-\stackrel{\to }{x_{nl}}\right)\right|$, where $k$ and $l$ are the indexes of different particles in a swarm. If $\left|S_n\right|<r_{conv}$, then the $n$-th swarm is marked as converged, and if all swarms are converged, then the worst of them is reinitialized.

The mQSO algorithm is one of the standard approaches for dynamic optimization due to its simplicity and high efficiency. The latter is due to the fast convergence of the standard PSO procedure, which is suitable for dynamic environments with rapid changes. However, the exploitative properties of mQSO may result in premature convergence and difficulties in identifying peaks positions in complex terrains. One of the ways to balance the mentioned problems is to use adaptive tuning schemes for local search step around best particles, i.e. generating quantum particles.

In the proposed modification mQSO-SHA, inspired by the SHADE algorithm (Tanabe & Fukunaga, 2013), the uniform distribution is changed to normal distribution with zero mean and standard deviation $r_{cloud}$, i.e. the new particles are generated as $\stackrel{\to }{x_q}\in \stackrel{\to }{p_{ng}}+N\left(0,r_{cloud}\right)$. The $r_{cloud}$ parameter is sampled independently for every generated particle: $r_{cloud}$= $N\left({Mr}_h,0.25\right)$, where ${Mr}_h$ is a memory cell with index $h$, chosen randomly. The values in the memory cells are initially set to ${Mr}_i=1$, $i=\mathrm{1,2},\dots H$, where $H$ is the memory size.

After every successful generation of a local search particle, i.e. when it is better than the global best, the value of $r_{cloud}$ and fitness improvement $|f\left(\stackrel{\to }{x_{ni}}\right)-f\left(\stackrel{\to }{p_{ng}}\right)|$ are stored to $S_r$ and $S_{im}$. At the end of every iteration, or after every environmental change, the $S_r$ and $S_{∆f}$ values are used to update the $k$-th memory cell using weighted Lehmer mean:

${Mr}_k^{it+\mathrm{1}}=\mathrm{0.5}({Mr}_k^{it}+\frac{\underset{j=\mathrm{1}}{\overset{\left|S_r\right|}{\sum }}{w}_j{S}_j^{\mathrm{2}}}{\underset{j=\mathrm{1}}{\overset{\left|S_r\right|}{\sum }}{w}_j{S}_j})$,

where $w_j=\frac{S_{∆f,j}}{\underset{l=1}{\overset{\left|S_{∆f,j}\right|}{\sum }}{S}_{∆f,l}}$, $it$ is the iteration number. The index of the updated memory cell is iterated after every update and reset to $1$ once it reaches $H$. The success-history adaptation moves the generated values of $r_{cloud}$ towards more successful, and the same memory cells are used for all swarms.

Findings

The computational experiments were performed on a set of benchmark problems generated by GMPB for CEC 2022 competition on DOPs. The 12 problem instances are characterized by different number of peaks, change frequency, shift severity and dimension. Table 1 shows the used parameters.

The following parameters have been set for the mQSO-SHA algorithm: $N_s=10$, $w=0.7298$, $c_1=2.05$ and $c_2=2.05$, $H=5$, $r_{cloud}=1$, number of environments was equal to 100, and number of independent runs was set to 31. The population size $N_p$ and the number of quantum particles $N_q$ were varied in the experiments.

To measure the performance of tested algorithm versions the offline error value was calculated:

$E_O=\frac{\mathrm{1}}{T\tilde{v}}\underset{t=\mathrm{1}}{\overset{T}{\sum }}\underset{\phi =\mathrm{1}}{\overset{\tilde{v}}{\sum }}\left({f^{\left(t\right)}\left({\stackrel{\to }{x}}^{\circ \left(t\right)}\right)-f}^{\left(t\right)}\left({\stackrel{\to }{x}}^{\mathrm{*}\left(t-\mathrm{1}\right)\tilde{v}+\phi }\right)\right)$,

where ${\stackrel{\to }{x}}^{\circ \left(t\right)}$ is the optimum position and ${\stackrel{\to }{x}}^{*\left(t\right)}$ is the best found solution at time,.

To test different configurations of mQSO and mQSO-SHA the population size $N_p$ was changed from 5 to 25, and the number of quantum particles $N_q$ changed from 1 to 10. To compare different parameter settings the Mann-Whitney rank sum statistical test with tie-breaking and normal approximation was applied. The normal approximation allows calculating the standard score $Z$ values of pairwise comparisons between different parameter settings. Figure 1 shows the heatmap of comparison of standard settings and other values, $Z$ scores are summed over all 12 test cases.

See Full Size >

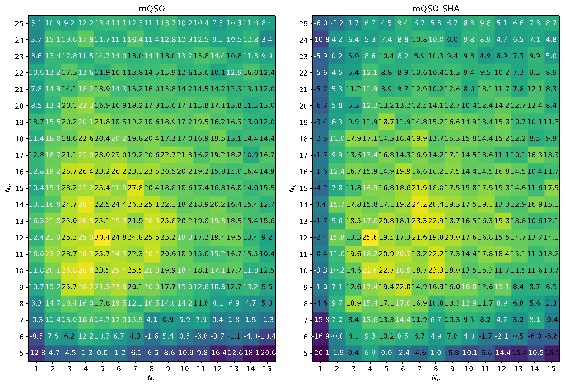
The results in Figure 1 demonstrate that the area of optimal values for population size and number of quantum particles lies around $N_p=12$, $N_q=5$ for mQSO, and $N_p=12$, $N_q=4$ for mQSO-SHA. Figure 2 shows the comparison of mQSO-SHA against standard mQSO with the same $N_p$ and $N_q$ in two cases, with standard shift severities and increased by 5 times.

The heatmaps in Figure 2 show that as the shift severity increases, the influence of the quantum particles increases too, and the parameter adaptation has more influence on the final result.

Table 2 provides the results of statistical tests (wins/ties/losses denoted as +/=/-) of the best mQSO against the best mQSO-SHA variants in both standard and increased shift severity scenarios.

See Full Size >

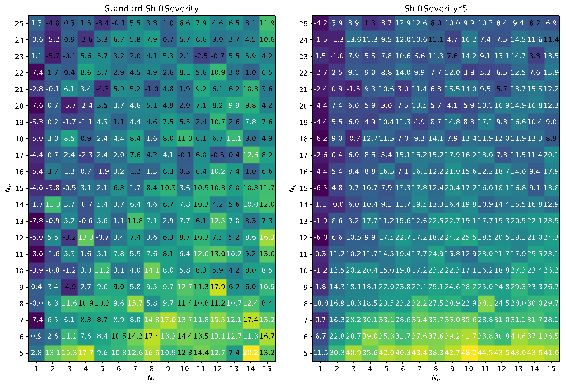
Table 2 shows that with standard shift severities the modified mQSO-SHA algorithm is better than mQSO only for F9 and F12, where the dimension or the shift severity is larger than in other cases. If the shift severity is increased by a factor of 5, the mQSO-SHA works better for 5 cases out of 12.

To show the process of parameter adaptation on different test cases, the graphs of parameter values are demonstrated in Figure 3.

See Full Size >

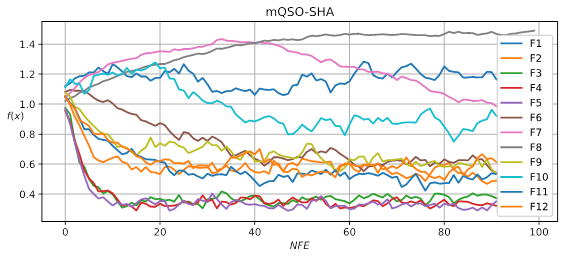
The graphs in Figure 3 demonstrate that for some of the test cases the $Mr$ values are decreased, while for other they are increased by parameter adaptation. Some of the interesting cases are F7, where first $Mr$ values are increased, and after 40% of the computational resource these values are decreased.

Conclusion

In this study, the modification of the multi-swarm QSO algorithm was proposed, in which the parameter of generating quantum particles has been tuned by success-history adaptation mechanism. The experiments, performed on a benchmark of dynamic optimization problems, have shown that the proposed mQSO-SHA algorithm is superior compared to the standard mQSO, especially in cases with large shift severity. The proposed modification can be included into other dynamic optimization methods based on mQSO to further improve their overall performance.

Acknowledgments

The reported study was funded by RFBR and FWF according to the research project №21-51-14003 and the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.

References

• Blackwell, T., & Branke, J. (2006). Multiswarms, exclusion, and anti-convergence in dynamic environments. IEEE Transactions on Evolutionary Computation, 10(4), 459-472. DOI:

  Google Scholar

  Crossref

• De Jong, K. (1999). Evolving in a changing world. Lecture Notes in Computer Science, 512-519. DOI:

  Google Scholar

  Crossref

• Huang, C., Li, Y., & Yao, X. (2020). A Survey of Automatic Parameter Tuning Methods for Metaheuristics. IEEE Transactions on Evolutionary Computation, 24(2), 201-216. DOI:

  Google Scholar

  Crossref

• Nguyen, T. T. (2011). Continuous dynamic optimisation using evolutionary algorithms [Doctoral Dissertation]. University of Birmingham.

• Nguyen, T. T., Yang, S., & Branke, J. (2012). Evolutionary dynamic optimization: A survey of the state of the art. Swarm and Evolutionary Computation, 6, 1-24. DOI:

  Google Scholar

  Crossref

• Tanabe, R., & Fukunaga, A. (2013). Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, 71-78. IEEE Press. DOI:

  Google Scholar

  Crossref

• Yazdani, D., Omidvar, M. N., Cheng, R., Branke, J., Nguyen, T. T., & Yao, X. (2020). Benchmarking Continuous Dynamic Optimization: Survey and Generalized Test Suite. IEEE Transactions on Cybernetics, 52(5), 3380-3393. DOI:

  Google Scholar

  Crossref

• Yazdani, D., Branke, J., Omidvar, M. N., Li, X., Li, C., Mavrovouniotis, M., Nguyen, T. T., Yang, S., & Yao, X. (2021). IEEE CEC 2022 competition on dynamic optimization problems generated by generalized moving peaks benchmark, arXiv preprint arXiv:2106.06174.

• Yazdani, D., Cheng, R., Yazdani, D., Branke, J., Jin, Y., & Yao, X. (2021a). A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades —Part B. IEEE Trans. Evol. Comput., 25, 630-650. DOI:

  Google Scholar

  Crossref

• Yazdani, D., Cheng, R., Yazdani, D., Branke, J., Jin, Y., & Yao, X. (2021b). A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades—Part A. IEEE Trans. Evol. Comput., 25, 609-629. DOI:

  Google Scholar

  Crossref

• Yazdani,