Abstract
The paper is devoted to the study of the influence of class imbalance on the quality of hydrocracking unit failure prediction models. The use of machine learning methods finds an increasing response in various industries due to the increase in computing power and the reduction in the cost of creating advanced process control systems. The oil and gas industry are highly profitable and large in terms of its industrial capacity; thousands of pieces of technical equipment within one enterprise are involved in the production of petroleum products and their processing. Therefore, improving the operational reliability of oil refining process equipment is an urgent scientific task. In this paper, we consider a method for modeling a hydrocracking unit for the production of diesel fuels and creating models for predicting plant equipment failures. Particular attention is paid to the influence of class imbalance in data when solving the classification problem. The built-in weighting methods for classes of machine learning models are compared, as well as upsampling and downsampling methods.
Keywords: Hydrocracking unit, machine learning, classifier, upsampling, downsampling
Introduction
Technological installations and oil refineries are designed to implement the processing of hydrocarbon raw materials into marketable products or semi-finished products for further conversion. The elements of this technological system include not only the main equipment (columns, reactors, technological pipelines, tanks, pumping and compressor equipment, etc.), but also technological equipment (power supply equipment, instrumentation systems, water supply and sewage and etc.).The number of elements of an oil refinery process unit that can to some extent affect the occurrence and development of an emergency, depending on the complexity of the installation, can reach from several hundred to thousands. In this regard, the analysis of the reliability of such technological systems is a rather complicated task, requiring knowledge of the technology, the features of the system elements and their interconnection. At present, for complex technical systems of the aviation and space industries, nuclear power engineering, the reliability analysis methodology has been developed and tested quite widely (Barabady & Kumar, 2008; Jun & Huibin, 2012; Meng et al., 2019)
The most promising are the methods based on the predictive approach - the methods of predicting failures. Recently, the use of machine learning models for analyzing large amounts of data, searching for statistical patterns and predicting equipment parameters or the state of the system as a whole has been in great demand (Jin et al., 2021; Salfner et al., 2010; Zhang et al., 2016).
Also relevant is the issue of reducing harmful emissions and reducing the carbon footprint from human activities. A lot of research is currently being done on the production of biofuels. Components for the production of biofuel compositions - biodiesel are produced using a hydrocracking unit (Al-Muttaqii et al., 2019; Hasanudin et al., 2022; Srihanun et al., 2020)
Problem Statement
The research problem is the insufficient reliability of the process equipment of the oil refining industry.
Research Questions
For this, the following questions need to be considered:
- Conduct a simulation of a hydrocracking unit.
- Simulate various installation scenarios.
- Obtain data on equipment failures during operation of the hydrocracking unit.
- Build failure prediction models using machine learning methods.
- Consider the impact of class imbalance when solving the classification problem
- Compare the performance of different machine learning models
Purpose of the Study
The purpose of the work is to study the effect of class imbalance when creating machine learning classification models for predicting failures of hydrocracking process equipment.
Research Methods
Simulation of the hydrocracking process
To create a unit model based on the flow chart of hydrocracking, we use the Aspen Hysys program. The basic technological scheme of the hydrocracking unit contains 3 main blocks: a reactor block, a separation block and a rectification block (Nakamanuruck et al., 2017).
Preparation, processing of data and creation of models
Simulation of 1000 installation scenarios will be carried out using the built-in scenario manager Aspen Simulation Workbook (Nekrasov et al., 2021).
Data processing, dataset creation is carried out in the Python programming language. To create forecasting models, we use the scikit-learn library (Nekrasov et al., 2022).
Metrics for evaluating the quality of models
To assess the quality of models, we use the indicators accuracy, precision, recall and F-score.
Based on the prediction results, you can get a matrix of model classification confusions (Table 1).
Thus, there are two types of classification errors: false negatives (FN) and false positives (FP).
Accuracy - proportion of correct answers of the algorithm. Precision can be interpreted as the proportion of objects that are called positive by the classifier and are actually positive. Recall - shows what proportion of objects of a positive class out of all objects of a positive class was found by the algorithm:
The F-score is the harmonic mean between precision and recall. It tends to zero if precision or recall tends to zero. AUC ROC - area under the curve receiver operating characteristic. This curve is a line from (0;0) to (1;1) in True Positive Rate (TPR) and False Positive Rate (FPR) coordinates:
Class imbalance
If the classes are unbalanced - a multiple excess of the number of output values of one class over another, this can affect the efficiency of the model.
To offset this influence, we use the methods of downsampling and upsampling.
- Downsampling - reducing the number of rows of the highest class by removing data to obtain a balance of classes.
- Upsampling - copying rows with data of a smaller class to get a balance.
- Also, some classification models have a built-in "class weight" hyperparameter, so let's consider the effectiveness of its application.
Findings
Hydrocracking unit model
The following model of the hydrocracking unit was obtained (Figure 1).
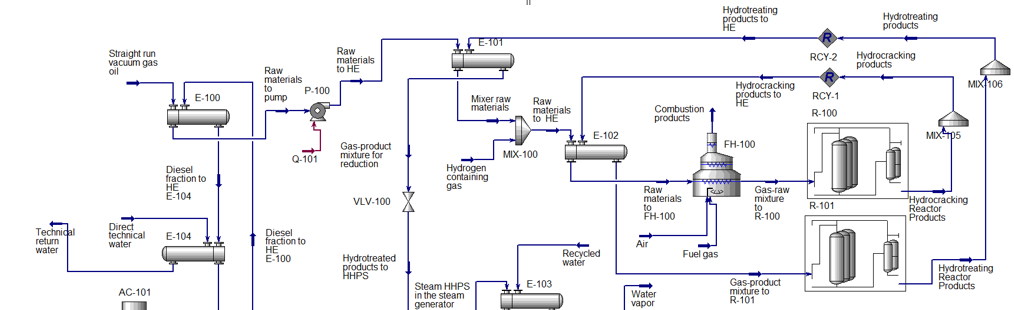
Dataset
The key parameters were determined, 8 input parameters - technological parameters of input flows, pressure and volume flow at the inlet to the reactor block and 1 output - the state of the system, the presence or absence of a failure. The dataset contains 1000 rows.
Models
Before training the model, the data were scaled, and normalized. Additional noise was applied to the data after generation in order to simulate possible data distortions in reality and to avoid overfitting the models on perfect data. The dataset is divided into training, test and validation samples in the ratio of 60:20:20. Models were created based on the decision tree, random forest, logistic regression and Gaussian Bayesian algorithms. For each model, the best set of hyperparameters was selected using the GridSearchСV algorithm. The number of model training sessions conducted varies from tens to several thousand, depending on the number of hyperparameters iterated (f. e. 2 hyperparameters for logistic regression and 5 hyperparameters for random forest). The evaluation indicators of the best models are presented in Table 2.
Figure 2 shows the roc-curves of the models:
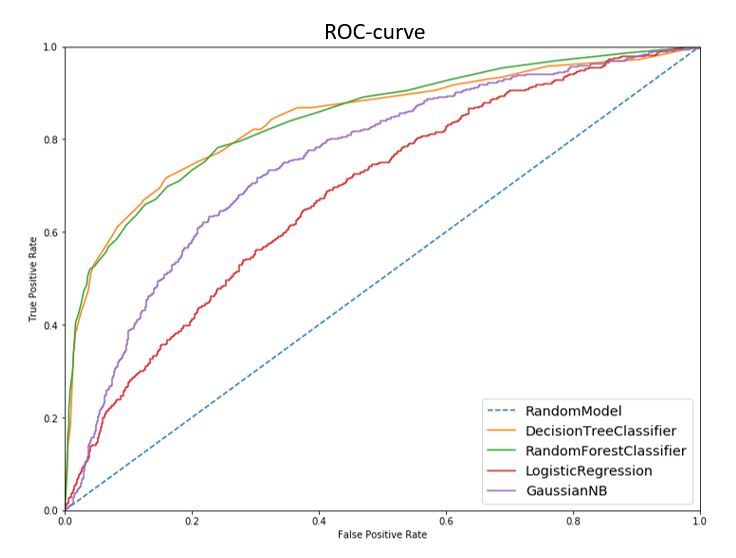
The random forest model showed the best result with the following set of hyperparameters: max_depth = 7; max_features = ‘sqrt’; min_samples_leaf = 3; min_samples_split = 7; n_estimators = 153.
Class imbalance
Ratio of model classes is 911 to 89. For alignment, you need to increase the number of class 1 values or decrease the class 0 values by a factor of 10. To do this, delete the rows or multiply the missing ones and then shuffle the data using the shuffle method. We also use the built-in model hyperparameter, where possible, class_weight = 'balanced'.
The metrics of the transformed models are presented in Table 3.
The F-measure fell for the decision tree and random forest, but increased significantly for the logistic regression. Gaussian Bayesian model has no model weight setting option. The logistic regression and Gaussian downsampled model model scores increased. The decision tree and random forest performed worse. F-measure improved for random forest, logistic regression, and Gaussian upsampled model compared to imbalanced data. The best F-measure model was a random forest with training data where class 1 was increased (Figure 3)
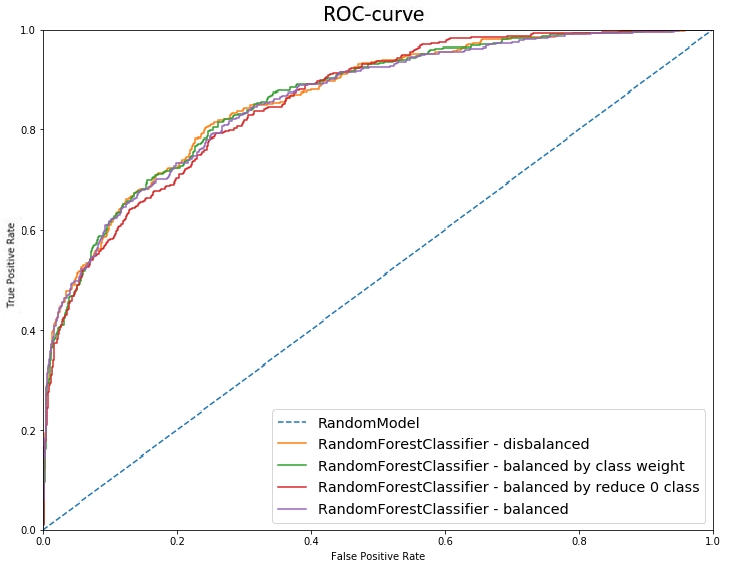
The imbalance affected the models for the worse. The best solution was to increase classes 1 in the training sample. The alignment of classes in the sample led to a sharp increase in the recall parameter and a slight decrease in precision. But in general, the F-score has grown.
Conclusion
According to the results of the work, a model of a hydrocracking unit in Aspen Hysys was created. Scenarios of operation and failures of the installation have been worked out, a dataset has been created based on these data Training of classification models based on decision tree, random forest, logistic regression, Gaussian-Bayesian algorithms. The influence of class imbalance on the quality of model forecasting was studied.
Class weighting improves the performance of models. Precision is falling, recall is growing, but in general, the F-score has a small increase. The balance of classes increases the coverage of the required data. Assessing the adequacy of the model, it can be noted that the AUC-ROC of the unbalanced model and the weighted model approximately equally predict the class of the plant state. As a result of the study, a model was obtained with the best performance both in terms of F-score and AUC-ROC - Random forest: balanced by grow 1 class. Model F-score increased from 0.625 to 0.635, AUC-ROC from 0.844 to 0.852.
Acknowledgments
This study is carried out under the state assignment under the project “Development of a set of scientific and technical solutions in the field of creating biofuels and optimal biofuel compositions that provide the possibility of transforming consumed types of energy carriers in accordance with energy efficiency trends, reducing the carbon footprint of products and using alternative fuels to fossil fuels” (FSRZ Contract -2021-0012) in the scientific laboratory of biofuel compositions of the Siberian Federal University, created as part of the activities of the Research and Educational Center "Yenisei Siberia".
References
Al-Muttaqii, M., Kurniawansyah, F., Prajitno, D. H., & Roesyadi, A. (2019). Bio-kerosene and Bio-gasoil from Coconut Oils via Hydrocracking Process over Ni-Fe/HZSM-5 Catalyst. Bulletin of Chemical Reaction Engineering & Catalysis, 14(2), 309. DOI: 10.9767/bcrec.14.2.2669.309-319
Barabady, J., & Kumar, U. (2008). Reliability analysis of mining equipment: A case study of a crushing plant at Jajarm Bauxite Mine in Iran. Reliability Engineering & System Safety, 93(4), 647-653. DOI:
Hasanudin, H., Asri, W. R., Zulaikha, I. S., Ayu, C., Rachmat, A., Riyanti, F., Hadiah, F., Zainul, R., & Maryana, R. (2022). Hydrocracking of crude palm oil to a biofuel using zirconium nitride and zirconium phosphide-modified bentonite. RSC Advances, 12(34), 21916-21925. DOI:
Jin, X., Chen, Y., Wang, L., Han, H., & Chen, P. (2021). Failure prediction, monitoring and diagnosis methods for slewing bearings of large-scale wind turbine: A review. Measurement, 172, 108855. DOI:
Jun, L., & Huibin, X. (2012). Reliability Analysis of Aircraft Equipment Based on FMECA Method. Physics Procedia, 25, 1816-1822. DOI:
Meng, D., Yang, S., Zhang, Y., & Zhu, S.-P. (2019). Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue & Fracture of Engineering Materials & Structures, 42(6), 1219-1227. DOI:
Nakamanuruck, I., Rungreunganun, V., & Talabgaew, S. S. (2017). Reliability analysis for refinery plants. Applied Science and Engineering Progress, 10(1). DOI:
Nekrasov, I., Tynchenko, V., Bukhtoyarov, V., Panfilova, T., Sokolnikov, A., Gorodov, A., & Panfilov, I. (2021). Simulation of the hydrocracking process to produce diesel fuel in the aspen hysys system. In press.
Nekrasov, I. S., Tynchenko, V. S., Bukhtoyarov, V. B., Kachaeva, V. A., Bashmur, K. A., & Sinitskaya, A. E. (2022). Applying Predictive Machine Learning Algorithms to Petroleum Refining Processes as Part of Intelligent Automation. 2022 IEEE 23rd International Conference of Young Professionals in Electron Devices and Materials (EDM) (pp. 599-604). DOI:
Salfner, F., Lenk, M., & Malek, M. (2010). A survey of online failure prediction methods. ACM Computing Surveys, 42(3), 1-42. DOI:
Srihanun, N., Dujjanutat, P., Muanruksa, P., & Kaewkannetra, P. (2020). Biofuels of Green Diesel-Kerosene-Gasoline Production from Palm Oil: Effect of Palladium Cooperated with Second Metal on Hydrocracking Reaction. Catalysts, 10(2), 241. DOI:
Zhang, K., Xu, J., Min, M. R., Jiang, G., Pelechrinis, K., & Zhang, H. (2016). Automated IT system failure prediction: A deep learning approach. 2016 IEEE International Conference on Big Data (Big Data) (pp. 1291-1300). DOI:
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Nekrasov, I., Bukhtoyarov, V., & Eremeeva, S. (2023). Influence of Class Imbalance on the Quality of Hydrocracking Unit Failure Prediction Models. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 178-185). European Publisher. https://doi.org/10.15405/epct.23021.22

