Abstract
Determining the step length in iterations of nonlinear minimization represents a problem that is not uniquely defined. Motivated by such uncertainty in defining step length, our intention was to use the capabilities of neutrosophy in this process. Our idea is to unify the usability and numerous applications of neutrosophic logic and the enormous importance of nonlinear optimization. An improvement of line search iteration for solving unconstrained optimization is proposed using appropriately defined Neutrosophic logic system in determining appropriate step size for the class of descent direction methods. The basic idea is to use an additional parameter that would monitor the behavior of the objective function and, based on that, correct the step length in known optimization methods. Mutual comparison and analysis of generated numerical results reveal better results generated by the suggested iterations compared to analogous available iterations considering the statistical ranking technique. Statistical measures show advantages of fuzzy improvements of considered line search optimization methods.
Keywords: Unconstrained optimization, neutrosophic logic systems, fuzzy logic systems, gradient descent methods
Introduction
Let denote the universe of discourse and assume . The fuzzy set theory is based on the use of a membership function (Zadeh, 1965). A fuzzy set in is a set of ordered pairs
Apart from the membership function , an intuitionistic fuzzy set (IFS) also uses the opposite non-membership function (Atanassov, 1986). More precisely, an IFS in is defined as
Smarandache (2003) and Wang et al. (2010) extended the IFS theory by initiating the indeterminacy-membership function, which represents indecisiveness in decision-making. Consequently, each element of a set in the neutrosophic set theory is defined by three independent membership functions (Smarandache, 2003; Wang et al., 2010): the truth-membership function , the indeterminacy-membership function , and the falsity-membership function. A single valued neutrosophic set (SVNS) over is the set of neutrosophic numbers of the form Values of these functions are independent and inside , which means and .
Fuzzy logic (FL), intuitionistic fuzzy logic (IFL) and Neutrosophic logic (NL) appear as efficient tools to handle mathematical models with uncertainty, fuzziness, ambiguity, inaccuracy, incomplete certainty, incompleteness, inconsistency, redundancy.
Neutrosophic sets (NS) have important applications for denoising, clustering, segmentation, and classification in numerous medical image-processing applications. A utilization of neutrosophic theory in denoising medical images and their segmentation was proposed in (Guo et al., 2009), such that a neutrosophic image is characterized by three membership sets. Several applications of of neutrosophic systems were described in (Christianto & Smarandache, 2019). An application of neutrosophy in natural language processing and sentiment analysis was investigated in (Mishra et al., 2020).
Our goal in the present paper is to unify possibilities of neutrosophy and several fradient-descent methods for solving unconstrained optimization problems.
Problem Statement
Our idea must be seen from two sides. First, we are guided by the huge popularity and numerous applications of NL. The other side of our problem is the ubiquitous optimization with a primordial desire to make the phenomenon or process the best possible. A combination of these two areas initiates applications of the Neutrosophic logic in determining an additional step size in main methods for solving the multivariate unconstrained optimization problem
(1)
with the objective .
The descent direction (DD) iterative flow is defined by
(2)
in which is the new approximation, is the former approximation, is a step size, and is an appropriate search direction. The vector must satisfy the so called descent condition , assuming that is the gradient vector of in the point . The choice of the anti-gradient direction leads to the gradient descent (GD) iterations
(3)
The general quasi-Newton (QN) class of iterations with line search
(4)
utilizes an appropriate symmetric and positive-definite estimation of the Hessian and then defines k (Sun and Yuan, 2006). The upgrade from is established on the QN characteristic
(5)
We will consider the scalar Hessian approximation (Nocedal and Wright, 1999):
(6)
where is the identity matrix. Consequently, iterations under detailed consideration in this paper are given as
(7)
and are known as (IGD) iterations. The quantity is defined as the output of an inexact line search, while is calculated based on Taylor series of .
Diverse forms and improvements of the IGD iterative scheme (7) were suggested in (Petrović et al., 2018; Stanimirović & Miladinović, 2010). The SM iterative flow is originated in (Stanimirović & Miladinović, 2010) and determined by the recurrence rule
(8)
where is the gain parameter determined utilizing the Taylor approximation of , as
such that , and
The following modification of the SM method was defined in (Ivanov et al., 2021) as the transformation defined by
(9)
where is the output of the line search, and
(10)
We propose improvements of surveyed line search iterative rules defined on the pattern (2) for solving (1). The principal idea is based on the utilization of an appropriate NLS in determining appropriate step length for various gradient descent rules. Fuzzy descent direction (FDD) iterations are defined as a modification of the DD iterations (2), as follows
(11)
where is appropriately defined adaptive Neutrosophic logic parameter. The set of desirable values of is defined upon the general restrictions
(12)
The second approach is based on
(13)
Both approaches reduce the step length if the objective function increases. The difference is that the first approach tends to increase the step size in the case where the objective function is decreasing, while the second approach leaves such cases to the original model. We will use the restrictions (12) in numerical comparisons.
The parameter will be determined using appropriately developed Neutrosophic logic controller (NLC). To our knowledge, such an research strategy has not been exploited so far.
Research Questions
Our exploratory research concerns the problem of determining the step length in (2). It is a known fact that the optimal step length determined on the basis of one-dimensional optimization is not an efficient solution in (Nocedal & Wright, 1999; Sun & Yuan, 2006). The problem of determining the step length is solved by the ILS procedure, which is guided by the basic principle that an appropriate step size initiates a substantial decrease in the value of the objective. Therefore, in this space of uncertainty, the possibility always remains open for additional improvements in the step size selection. eventually,there is no general rule to predict in each iteration of each individual method.
A neutrosophic logic system (NLS) is helpful in such situations that certainly cannot be predicted nor determined. Motivated by such a situation, we are sure that an NLS developed in a proper way is a suitable tool to define an additional gain parameter dynamically on the basis of previous results of the objective . The basic dilemma is how to determine the value as an output of appropriately defined NLS in each iterative stage of the flow (11), such that the final searching step forces more rapid decreases of the objective . Our goal is to investigate some possibilities for defining proper NLS, define an additional parameter in main IGD methods and compare their effectiveness with respect to original methods.
Purpose of the Study
An NL is a better choice than the FL and IFL in representation of real world data and their executions because of several reasons, as follows.
We originate and investigate a correlation between possibilities of NLSs and main methods available in nonlinear optimization. To be more precise, we will show that the learning rate parameter can be supported during iterative process using an appropriate value which is determined as the output of appropriately defined NLS that involves appropriately determined membership functions .
Research Methods
The first research method is a rigorous convergence analysis based on mathematical analysis.
The second research method assumes numerical testing and comparison of obtained numerical data. Test problems in ten dimensions are evaluated and average values are used. The Codes Are Tested In Matlab R2017A.
The third method comprises comparison based on the statistical ranking of the proposed optimization methods against corresponding known methods.
Findings
In this section we define three NLC-based optimization methods and describe the principles of the NLS used in defining the parameter .
NLC-based optimization methods
Fuzzy GD method (FGD) is determined by the iterative sequence
(14)
Fuzzy SM method (FSM) is defined as
(15)
where
(16)
The Fuzzy MSM method (FMSM) is defined by
(17)
where
(18)
The overall structure of optimization methods defined on the usage of NLS follows the philosophy described in the diagram of Figure 1.
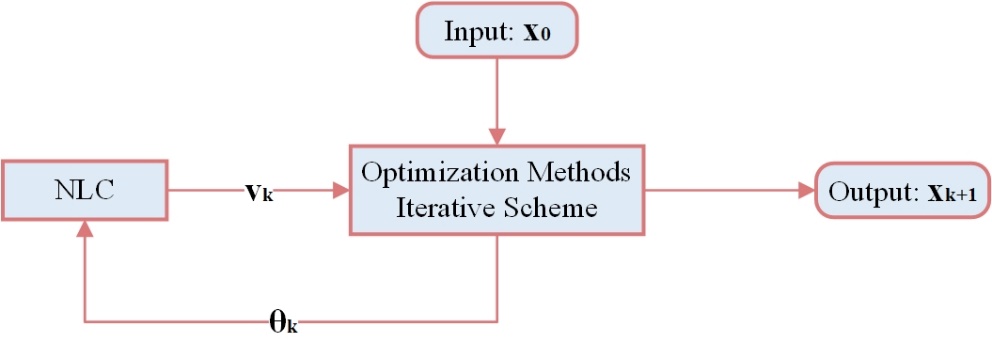
Neutrosophic logic system
To define the FMSM method, we need to define the steps Score function, Neutrosophistication and De-Neutrosophistication.
. Using three membership functions, neutrosophic logic maps the input into neutrosophic triplets . There are a huge number of convenient membership functions that can be used. Our empirical experience based on a large number of numerical tests led us to the following choice.
The truth-membership function is defined as the sigmoid function:
(19)
The parameter is responsible for its slope at the crossover point . The falsity-membership function is the sigmoid function:
(20)
The indeterminacy-membership function is the Gaussian function:
(21)
where the parameter signifies the standard deviation, and denotes the mean. In general, the neutrosophication of the crisp value is its transformation into , where the membership functions are defined in (19), (20) and (21).
Since the final goal is to minimize , it is a straightforward decision to use as a measure in the developed NLC.
: The neutrosophic rule between the input fuzzy set and the output fuzzy set under the neutrosophic format is described by the following "IF-THEN" rules:
The notations and stand for fuzzy sets, and indicate a positive and negative error, respectively.
. This step applies conversion resulting into a crisp real quantity .
The following which satisfies the requirement (12) is proposed to obtain the parameter :
(22)
where .
Statistical ranking
We compare six methods, of which three are FMSM, FSM, and FGD based on appropriately defined NSL, while the other three MSM, SM, and GD methods are well known in the literature. To this aim, we perform competitions on standard test functions with given initial points from (Andrei, 2008; Bongartz et al., 1995). We compare MSM, SM, GD, FSM, FGD, and FMSM methods in three decisive criteria: The CPU time in seconds - CPUts; the number of iterative steps - NI; the number of function evaluations - NFE.
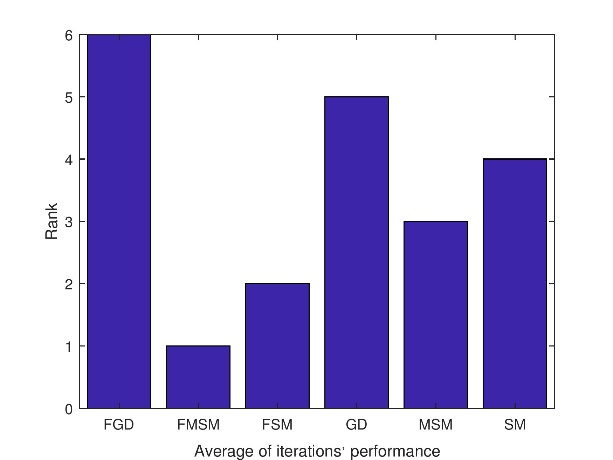
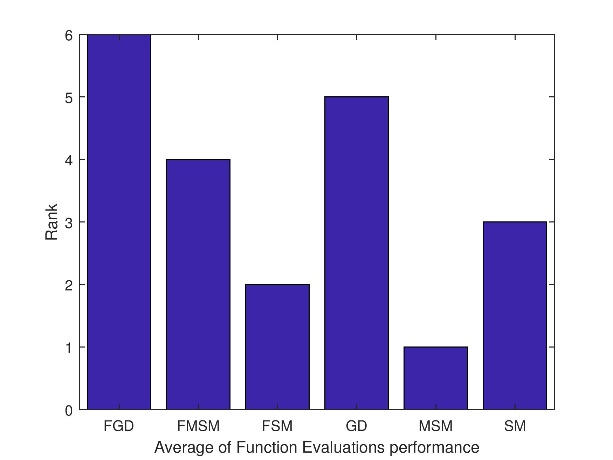
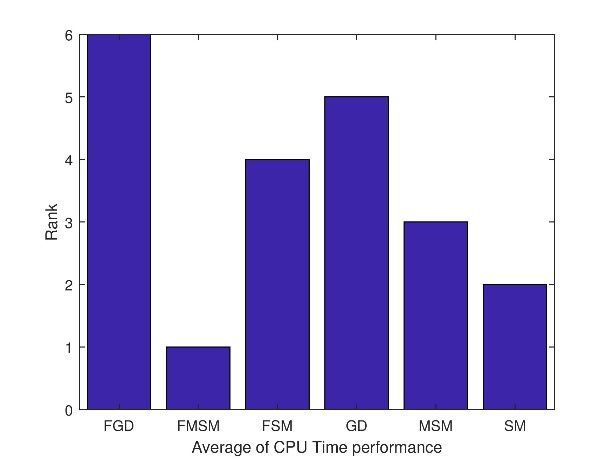
The performances of the optimization methods GD, SM, MSM and their fuzzy duals FGD, FSM, FMSM are ranked on solving the 30 test functions.
Figure 2 shows the iterations' performance rank of the optimization methods. Note that a method is regarded as rank 1 if it requires the fewest iterations out of all the considered methods. If a method has the second-fewest iterations compared to all the compared methods, it would be considered rank 2. The ranking process continues until the last method of rank 6. Figure 3 shows the function evaluations performance rank of the optimization methods. Figure 4 shows the CPU time consumption performance rank
The general observation is that the FMSM is the best with respect to iterations' performance and the CPU time consumption performance. On the other hand, the MSM has the best function evaluation performance.
Conclusion
Line search iterations for solving unconstrained optimization are improved utilizing an additional step parameter produced by appropriately defined netrosophic system. More precisely, using an appropriate neutrosophic logic, we propose a new approach in solving uncertainty in defining parameters involved in iterations for solving nonlinear optimization methods. The improvement is based on the utilization of the Neutrosophic logic in determining appropriate step size usable in various gradient descent methods.
Performed theoretical analysis reveals convergence of novel iterations under the same conditions as for corresponding original methods. Numerical comparison and statistical ranking indicate advantages of fuzzy and neutrosophic improvements of underlying line search optimization methods. Our numerical experience shows that the neutrosophic parameter is particularly efficient as an additional step size composed with previously defined parameters. Additional research can focus on neural network optimization (Mourtas & Katsikis, 2022b) or even portfolio optimization problems (Mourtas & Katsikis, 2022a).
Acknowledgments
Predrag Stanimirović is supported by the Science Fund of the Republic of Serbia, (No. 7750185, Quantitative Automata Models: Fundamental Problems and Applications - QUAM).
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).
References
Andrei, N. (2008). An unconstrained optimization test functions collection. Advanced Modeling and Optimization, 10(1), 147-161.
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy sets and systems, 20(1), 87-96. DOI:
Bongartz, I., Conn, A. R., Gould, N., & Toint, P. L. (1995). CUTE: Constrained and unconstrained testing environment. ACM Transactions on Mathematical Software (TOMS), 21(1), 123-160. DOI:
Christianto, V., & Smarandache, F. (2019). A review of seven applications of neutrosophic logic: In cultural psychology, economics theorizing, conflict resolution, philosophy of science, etc. Multidisciplinary Scientific Journal, 2, 128-137. DOI:
Guo, Y., Cheng, H. D., & Zhang, Y. (2009). A new neutrosophic approach to image denoising. New Mathematics and Natural Computation, 5, 653-662. DOI:
Ivanov, B., Stanimirović, P. S., Milovanović, G. V., Djordjević, S., & Brajević, I. (2021). Accelerated multiple step-size methods for solving unconstrained optimization problems. Optimization Methods and Software, 36(5), 998-1029. DOI:
Mishra, K., Kandasamy, I., Kandasamy W. B, V., & Smarandache, F. (2020). A novel framework using neutrosophy for integrated speech and text sentiment analysis. Symmetry, 12(10), 1715. DOI:
Mourtas, S. D., & Katsikis, V. N. (2022a). V-Shaped BAS: Applications on Large Portfolios Selection Problem. Computational Economics, 60(4), 1353-1373. DOI:
Mourtas, S. D., & Katsikis, V. N. (2022b). Exploiting the Black-Litterman framework through error-correction neural networks. Neurocomputing, 498, 43-58. DOI:
Nocedal, J., & Wright, S. J. (1999). Numerical Optimization. Springer-Verlag.
Petrović, M., Rakočević, V., Kontrec, N., Panić, S., & Ilić, D. (2018). Hybridization of accelerated gradient descent method. Numerical Algorithms, 79(3), 769-786. DOI:
Smarandache, F. (2003). A unifying field in logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability. American Research Press, Rehoboth.
Smarandache, F. (2016). Neutrosophic logic - A generalization of the intuitionistic fuzzy logic. DOI:
Stanimirović, P. S., & Miladinović, M. B. (2010). Accelerated gradient descent methods with line search. Numerical Algorithms, 54(4), 503-520. DOI:
Sun, W., & Yuan, Y.-X. (2006). Optimization Theory and Methods: Nonlinear Programming. Springer Optimization and Its Applications. Springer.
Wang, H., Smarandache, F., Zhang, Y. Q., & Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace and Multistructure, 4, 410-413.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338-353. DOI:
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Stanimirović, P. S., Ivanov, B., Katsikis, V. N., & Mourtas, S. D. (2023). Neutrosophy in Unconstrained Nonlinear Optimization. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 131-139). European Publisher. https://doi.org/10.15405/epct.23021.17

