Abstract
Many enterprises, including repair ones, face the problem of losses due to measurement errors. It has established that the number of losses from the measurement error has affected by the type (error) of the measuring instrument used, the dispersion of the controlled parameter (the distribution law, the scattering zone), and the features of the technological process. The article presents a generalized theoretical mathematical model developed by the authors, which describes the procedure for the formation of losses from measurement errors. The developed model has adapted in relation to repair production, using the example of controlling the diameters of the main journals of the crankshaft of the YaMZ-238 engine. The approbation of the developed technique made it possible to determine the losses from the measurement error in the control of the root diameters of the crankshaft journals using various measuring instruments. It has established that the greatest losses have obtained when using measuring instruments with the largest error, and the smallest ‒ with the smallest error. The use of a more accurate measuring instrument instead of the recommended one will reduce the losses from the measurement error during the input control of new crankshafts in the repair shop by more than 77%.
Keywords: Loss due to measurement error, measurement error, measurement of linear dimensions
Introduction
Measuring processes are an integral part of any technological process, they are necessary for quality control and management decisions. Any measurement result contains an error. Due to the presence of measurement errors and the dispersion of controlled quantities, there is a possibility of errors of the 1st and 2nd kind, these errors lead to losses. Losses due to measurement error have classified as follows:
- losses due to measurement error - when measuring equipment control parameters, final control and product quality control;
- loss, arising from measurement errors in the implementation of consumption, accounting and dosing;
- loss, deviation from the deviation of the technological process parameters from the optimal indicators due to measurement errors.
With regard to the control of the dimensions of parts, the probability of errors of the 1st and 2nd kind leads to the fact that some of the good parts can be rejected, and some of the defective ones fall into the good ones. In addition, losses from measurement errors can also have more serious consequences when, based on information about the controlled object, a conclusion is made about a batch of parts or products (Chiu et al., 2021; Razmkhahet al., 2021).
Problem Statement
Many businesses, including repair shops, face loss due to measurement errors, reading errors, or poor management of data collection systems (Alves et al., 2006; Chang & Hoi, 2001). In modern studies, issues related to the assessment of losses from measurement errors have considered from the standpoint of assessing the risks and opportunities of the process (Koksal et al., 2013; Koksoy et al., 2019). This approach makes it possible to consider measurement processes as processes of an enterprise management system and manage them in accordance with the requirements of ISO 9001 (Leonov & Shkaruba, 2020a). An analysis of existing methods for calculating losses due to measurement error showed that all of them are purely theoretical and do not take into account the specifics of a particular technological process (Wu, 2013). A feature of modern engineering production is the appointment of such tolerances that allow for a certain margin of accuracy in the joints (Leonov & Shkaruba, 2019; Leonov et al., 2020c), as well as the necessary accuracy of dimensional chains (Erokhin et al., 2021), but at the same time there is a decrease in tolerances, an increase in the accuracy of processing and, as a result, the need to use more accurate measuring instruments.
The object of research is the measurements carried out during the control of the linear dimensions of parts in the repair industry. The subject of research is economic losses from measurement errors.
Research Questions
The following questions had posed during the study:
- What factors influence the amount of loss due to measurement error?
- How to mathematically describe the order of loss formation in relation to a real measurement object?
- What are the economic losses from measurement errors in the control of a real object in repair production?
Purpose of the Study
Answers to the questions posed will allow solving the identified problems, developing and testing a methodology for assessing economic losses arising from measurement errors at each stage of control in repair production.
Research Methods
Theoretical and experimental methods were used in the research. Compiled and analyzed are mathematical models of the influence of measurement errors on the results of sorting parts in the repair industry. For the processing of experimental data, methods of probability theory, mathematical statistics, standard and specially developed algorithms, as well as a computer program developed in the Delthe7 environment had used.
Findings
Theoretical Substantiations of Losses from Measurement Errors
The measurement error during the input control of materials and the control of products during the technological process leads, firstly, to false rejection and loss of suitable materials or products, and secondly, to skipping unsuitable materials and semi-finished products for further processing, which leads to unnecessary costs for subsequent technological and control operations.
The output control error affects losses due to false rejection of finished products or losses associated with the passage of defective products to the consumer. The error in measuring the parameters of the technological process determines the percentage of the yield of good products in a given technological operation.
The frequency of control leaves an imprint on the number of rejected and missed products, including falsely rejected and missed defective ones.
The volume of the controlled object determines (together with the characteristics of the controlled parameter of the products and the measurement error) the probabilities of making decisions during the control, and, consequently, the proportion of rejected and accepted products.
The number of measured parameters during control determines the methods for calculating probabilistic characteristics and all the above-mentioned consequences of control.
The dependence of annual losses on the measurement error can be obtained as a result of (Leonov & Shkaruba, 2020a):
- conducting an appropriately planned active factorial experiment;
- theoretical analysis of the technological process, the parameters of which are measured during the process control;
- simulation of the procedure for optimizing the mode of the technological process using computer technology.
In general terms, annual losses from measurement error during the control operation have calculated by the formula
(1)
where – the total number of products subject to control during the year, pc.; – is the share of falsely rejected products from the total number;– average losses arising from false rejection of the product, rub./pc.; – share of defective products recognized as fit; – losses caused by the penetration of defective products into the production process or to the consumer, rub./pc.
Formula (1) describes only the general concept of losses. Let us consider the formation of these losses at a deeper level. Economic losses associated with the occurrence of control errors have due to the occurrence of defective products at a given technological operation and have defined as losses for the rejection of these products at subsequent technological or control operations, taking into account the probability of their detection at each operation:
(2)
where – losses when a defective product is detected at the subsequent-th operation, rub./pc.; – probability of detecting a defective product at the-th technological or control operation; – the number of control or technological operations where it is possible to detect a defective product that occurs in a given technological operation; – losses of the enterprise upon presentation of a claim or a fine in case of a defect found in the consumer, rub./pc.;– the probability of detecting a defective product at the output control operations or at the consumer.
Losses associated with incorrect rejection errors do not have a single calculation formula. Firstly, this is due to the fact that this category can have qualitatively different characteristics (incorrectly rejected parts that fall into the group of unrecoverable defects, incorrectly rejected parts that fall into the group of correctable defects) and, secondly, the losses will depend on the type of operation control and its place in the technological process (intermediate control or final control of finished products).
Economic losses on intermediate control operations as a result of the delay in the annual part of consumption:
for the case of falling into the group of irreparable defect
(3)
where – the cost of the part for the-th operation, rub.; – residual value (cost of scrap metal), rub.in the correctable defect group (4)
where – the cost of correcting the defect, rub.
Economic losses during the final control of finished products, when serviceable parts were rejected due to the influence of measurement errors:
for the case of falling into the group of a correctable defect:
(5)
where – costs for rechecking (sorting out) or reworking the product, rub.
to the group of an unrecoverable defect:
(6)
where – losses from the rejection of one product, numerically equal, in accordance with the procedure for the sale of defects:
the difference between the lowest quality category and the cost of parts:
= –, (7)
where – product selling price, rub.;
cost of the product minus the residual value:
= –, (8)
where – the probability that the part will be good.
Methodology for assessing losses from measurement error when controlling the diameters of the crankshaft journals
Formulas (1) - (8) are of a generalized nature, therefore, in order to calculate losses from measurement errors, these formulas must be adapted taking into account the specifics of the technological process. We will draw up a methodology for estimating losses using the example of controlling the diameters of the crankshaft journals during the overhaul of engines.
New crankshafts supplied for the acquisition of parts, assembly units and assemblies are subject to control. Errors that occur in this operation due to measurement errors lead to losses. Shafts that do not meet the requirements for manufacturing accuracy are returned to the supplier, including incorrectly rejected ones. Therefore, in the calculation of losses, we take into account only losses from errors associated with defective shafts accepted as good. These losses have calculated by the formula
(9)
where – losses when a defective shaft has detected at the stage of completing and assembling parts, assembly units and assemblies, rub.; – losses when a defective shaft is detected during running-in and testing (output control).
where – the number of new crankshafts received for control, rub.; – the probability that a defective shaft will be assigned to the group of suitable shafts coming for picking;– costs for completing and assembling parts, assembly units and assemblies, rub.; – cost of running in and testing the engine, rub.; – costs for fines and complaints from the consumer, rub.
Investigation of the Dependence of Losses on the Measurement Error in the Control of the Main Diameters of the Crankshaft Journals
To test the methodology, 100 crankshafts from YaMZ-238 NB engines had selected. The parameters of the studied parts have shown in Table 1.
A preliminary assessment was made of the dispersion of the dimensions of the main journals of the crankshaft. The distribution law and standard deviation have determined.
To study the dependence of losses on the measurement error during the control of the root diameters of the crankshaft journals, several measuring instruments were selected, several measuring instruments with different accuracy. In the technical requirements for the overhaul of engines, it has recommended to use micrometers to measure the diameters of the crankshaft journals. Therefore, a smooth micrometer of the MK type had adopted as the basic measuring instrument.
For comparison with the basic measuring instrument, the following have selected: one measuring instrument with an increase in error and four - with an error less than that of the basic measuring instrument. All selected measuring instruments are universal and have used when working in the hands. The selected measuring instruments and their metrological characteristics have shown in Table 2.
The initial data for calculating dependencies (9) - (12) have presented in Table 3. The results of the calculations have summarized in Table 4. To calculate the probability that a defective crankshaft journal will be recognized as suitable, a special computer program had used (Leonov & Shkaruba, 2020b).
On the basis of the calculated data, graphic dependences (Figure 1) of losses on the measurement error had constructed.
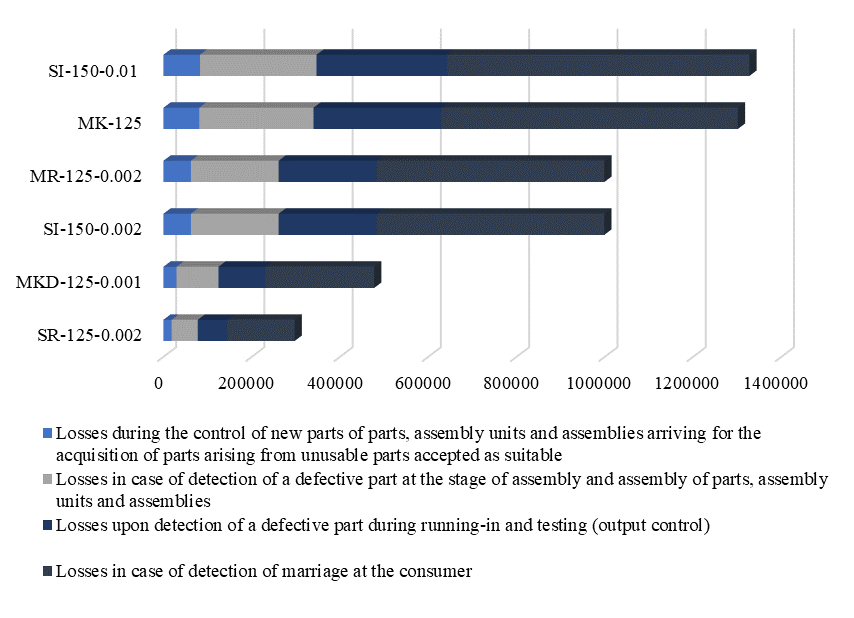
From the graphs presented in Figure 1, it can be seen that the largest losses have obtained when using measuring instruments with the largest error, and the smallest - with the smallest error. The percentage ratio of the specific components of losses from the measurement error remains constant and does not depend on the measuring instruments. The largest share of the measurement error falls on losses when a defective product has detected at the consumer (51.6%). The use of a more accurate measuring instrument (SR-125-0.002) instead of the recommended one (MK-125) will reduce the losses from the measurement error by more than 77%.
Conclusion
The conducted research made it possible to identify problems that arise at enterprises due to measurement errors. It has been established that the number of losses from the measurement error has affected by the type (error) of the measuring instrument used, the dispersion of the controlled parameter (the distribution law, the scattering zone), and the features of the technological process.
Taking into account the influencing quantities, a generalized mathematical model has been compiled that describes the order of loss formation. The compiled model is adapted in relation to repair production, using the example of controlling the diameters of the main journals of the crankshaft of the YaMZ-238 engine. The approbation of the developed technique made it possible to determine the losses from the measurement error in the control of the root diameters of the crankshaft journals using various measuring instruments. As a result of the research, it has found that the greatest losses are obtained when using measuring instruments with the largest error, and the smallest - with the smallest error.
References
Alves, R., Casanova, P., Quirogas, E., Ravelo, O., & Gimenez, W. (2006). Reduction of Non-Technical Losses by Modernization and Updating of Measurement Systems. Proceedings of the IEEE-PES Transmission & Distribution Conference and Exposition Latin America, 1-3, 256.
Chang, K. T. K. F., & Hoi, L. W. S. (2001). Measurement and Analysis Errors. International Society of Sugar Cane Technologists, 1, 345-346. https://api.semanticscholar.org/CorpusID:127774091
Chiu, YSP., Chiu, T., Pai, FY., & Wu, H. Y. (2021). A producer-retailer incorporated multi-item EPQ problem with delayed differentiation, the expedited rate for common parts, multi-delivery and scrap. International Journal of Industrial Engineering Computations, 12(4), 427-440.
Erokhin, M., Leonov, O., Shkaruba, N., Amelin, S., & Bodunov, D. (2021). Application of Dimensional Analysis for Calculating the Total Misalignment between a Seal and a Shaft. Journal of Machinery Manufacture and Reliability, 50(6), 524-529.
Koksal, G., Taseli, A., Dolgun, L. E., & Batmaz, I. (2013). The Effect of Inspection Error on Quality and Producer Losses: The Case of Nominal-the-Best Type Quality Characteristic and Rework. European Journal of Industrial Engineering, 7(4), 497-528.
Koksoy, O., Ergen, P., & Zeybek, M. (2019). A New Right-Skewed Loss Function in Process Risk Assessment. European Journal of Industrial Engineering, 13(4), 536-551.
Leonov, O., & Shkaruba, N. (2019). A Parametric Failure Model for the Calculation of the Fit Tolerance of Joints with Clearance. Journal of Friction and Wear, 40(4), 332-336.
Leonov, O., & Shkaruba, N. (2020a). Calculation of Fit Tolerance by the Parametric Joint Failure Model. Journal of Machinery Manufacture and Reliability, 49(12), 1027-1032.
Leonov, O., & Shkaruba, N. (2020b). Theoretical Basis of Selection of Measurement Measures in Control of Linear Sizes. Journal of Physics: Conference Series, 52081.
Leonov, O., Shkaruba, N., & Kataev Y. (2020c). Measurement Risk Management Method at Machine-Building Enterprises. Journal of Physics: Conference Series, 52060.
Razmkhah, M., Gildeh, B. S., & Ahmadi, J. (2021). An Economic Design of Rectifying Single Sampling Plans Via Maxima Nomination Sampling in The Presence of Inspection Errors. Communications in Statistics-Simulation and Computation, 50(1), 217-233.
Wu, C. W. (2013). Process performance evaluation based on Taguchi capability index with the consideration of measurement errors. International Journal of Systems Science, 44(8), 1386-1399.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
29 August 2022
Article Doi
eBook ISBN
978-1-80296-126-3
Publisher
European Publisher
Volume
127
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-496
Subjects
Economics, social trends, sustainability, modern society, behavioural sciences, education
Cite this article as:
Shkaruba, N., Leonov, O., Temasova, G., & Vergazova, Y. (2022). Evaluation Of Economic Losses From Measurement Error. In I. Kovalev, & A. Voroshilova (Eds.), Economic and Social Trends for Sustainability of Modern Society (ICEST-III 2022), vol 127. European Proceedings of Social and Behavioural Sciences (pp. 234-242). European Publisher. https://doi.org/10.15405/epsbs.2022.08.26

