Moment Ratio And Entropy Coefficient Display For Beta Distribution Of Second Kind

Model beta Distribution of the Second Kind and its Moments

In probability theory, the beta distribution of the second kind is an absolutely continuous probability distribution defined on the positive axis of real values (x> 0). A random variable X follows a beta distribution of the second kind with shape parameters of u and v that are more zero if its cumulative distribution function is defined as (Vadzinsky, 2001)

$F(x;u,v)=I_{x/(1+x)}(u,v)$ (1)

Where_/(1+) (,) are the ratios of the incomplete beta functions, that is given by

$I_z(u,v)=\frac{B_x(u,v)}{B(u,v)}=\frac{\mathrm{1}}{B(u,v)}{\int }_{\mathrm{0}}^z t^{u-\mathrm{1}}(\mathrm{1}-t{)}^{v-\mathrm{1}}dt$ (2)

Here(,) is the beta function given as an Euler integral of the first kind, and is first and second shape parameters.

The probability density of the standardized beta distribution of the second kind is associated with the cumulative probability function of (1) that is given by

$f(x,u,v)=\frac{1}{B(u,v)}·\frac{x^{u-1}}{(1+x{)}^{u+v}}$ (3)

The paper also notes the limited choice of the model, which, apparently, is due to the lack of formalized methods for analysing the shape of the model (Hertzler, 2003). For these purposes, methods are classically used that is based on distribution moments. The initial moment of order for the beta distribution of the second kind is given as the ratio of the beta functions (Bourguignon & de Castro, 2021)

$m_{xr}=\frac{B(u+r,v-r)}{B(u,v)},(-u)<r<v$ (4)

If the order of the moment is less than the second shape parameter, then to calculate the moment of the beta distribution of the second kind, you can use an expression of the shape

$m_{xr}={\prod }_{i=\mathrm{1}}^r \frac{u+i-\mathrm{1}}{v-i},\mathrm{}v>r$ (5)

Thus, it can be seen that the moments of the generalized scaled beta distribution of the second kind are proportional to the moments of the standard beta distribution that is determined only by the scaling parameter. In this case, the moments of the standardized beta distribution of the second kind are completely specified by the shape parameters. Since the arrays of real processes are always scaled, this creates difficulties in choosing the shape of the model and estimating its parameters directly from the observed results. For these goals, standardized moments are classically used, such as skewness and kurtosis.

In practice, when using different conventional units, the random variable is scaled with a scale parameter. Then the random variable is given as a product

$Y=\vartheta X$ ( 6 )

А scaled beta distribution of second kind is given as

$f(y;\vartheta ,u,v)=\frac{\mathrm{1}}{{\vartheta }^{u}B(u,v)}\cdot \frac{y^{u-\mathrm{1}}}{{\left(\mathrm{1}+{\vartheta }^{-\mathrm{1}}y\right)}^{u+v}}$ ( 7 )

The beta distribution density function (7) is convenient for modeling arbitrary scaled responses of complex systems given on the positive half-axis of values. When modeling the responses of real systems, the data is almost always scaled according to the chosen system of units. In most cases, using directly models based on a standardized beta distribution is not convenient due to the scaling the data. This limits the application of forms of beta distribution models in practice.

It is discussed in (Moghaddam et al., 2021) that if a stochastic volatility model is defined with the mean reverting multiplicative Heston (Johnson et al., 1994), then its stochastic differential equation is given by

$d{v}_t=-\gamma \left(v_t-\mathrm{\Theta }\right)dt+\sqrt{k_M^{\mathrm{2}}\cdot v_t^{\mathrm{2}}+k_H^{\mathrm{2}}\cdot v_t}\cdot dW$ ( 8 )

Where is the stochastic variance, is the relaxation time parameter, and are the weight coefficients of the multiplicative model and the Hestona model, is a normally distributed Wiener process, is the average value of the stochastic variance: =<>.

The parameters of the stochastic equation (8) completely determine the parameters of the beta distribution of the second kind (2). In case, if the relaxation time parameter is known and the parameters of the scaled beta distribution of the second kind (7) were estimated, then the weight parameters of the stochastic equation (8) are given as

$\begin{array}{rr}{k}_H& =\sqrt{\mathrm{2}\gamma (v-\mathrm{1}{)}^{-\mathrm{1}}}\\ k_M& =\sqrt{\mathrm{2}\gamma (v-\mathrm{1}{)}^{-\mathrm{1}}}\end{array}$ ( 9 )

The mean value of the stochastic variance is related to the scale parameter of the beta distribution of the second kind, which is given as

$\mathrm{\Theta }=u(v-\mathrm{1}{)}^{-\mathrm{1}}\vartheta .$ ( 10 )

Relations (9) and (10) allow us to calculate the parameters of the stochastic volatility equation model with known beta distribution parameters.

Standardized Moments

In probability theory, various methods of moments are traditionally used to study the distribution shape, that it is presented in Craig (1936), Han and Shapiro (1969), Kobzar (2006), Vadzinsky (2001). The method of moments was introduced by Pafnuty Chebyshev in 1887 when proving the central limit theorem (Chebyshev, 1955; Rybnikov, 1974). For data analysis and preliminary selection of a family of distributions in regression analysis, standardized normalized second, third, and fourth moments of distributions are used, which are known as the coefficient of variation, skewness and kurtosis of the distribution. These are the most important indices of the distribution shape. Expressions for calculating the standardized moment of the beta distribution of the second kind in many reference books on distributions are contained, for example (Gubarev, 1992; Vadzinsky, 2001).

For calculating of the third standardized moment, the expression of skewness is given as

$Sk=\frac{\mathrm{2}(\mathrm{2}u+v-\mathrm{1})}{(v-\mathrm{3})}\sqrt{\frac{v-\mathrm{2}}{u(u+v-\mathrm{1})}},\mathrm{}v>\mathrm{3}$ ( 11 )

For calculating the fourth standardized moment, the expression of kurtosis is defined as

$Ex=\frac{\mathrm{6}(v-\mathrm{1}{)}^{\mathrm{2}}(v-\mathrm{2})+u(\mathrm{5}v-\mathrm{11}\left)\right(u+v-\mathrm{1})}{u(u+v-\mathrm{3})(v-\mathrm{3})(v-\mathrm{4})},\mathrm{}v>\mathrm{4}$ ( 12 )

An important property of the standardized moments of equation (11) and equation (12) is that they are insensitive to changes in the distribution scale parameter. For this reason, the standardized moments of equation (11) and equation (12) are used for a preliminary assessment of the belonging of the sample data to the distribution model. For these purposes, the visualization of the parameter space is used, that was proposed by A. Rhind in 1909 for the Pearson distribution system. Rhind and Pearson used the third and fourth standardized moments as space coordinates (Pearson, 1895; Rind, 1909). Moment-ratio diagrams were later developed and popularized by Craig (1936), Han and Shapiro (1969), Johnson et al. (1994).

Anti-Kurtosis

The use of distribution kurtosis is not convenient for illustrating the position of models of beta distribution of the second kind, since theoretically the kurtosis tends to infinity, provided that the first shape parameter tends to zero. This is due to the presence of tails of the distribution that is slowly converging to zero. In the region of constraints of the second shape parameter, the kurtosis is positive and greater than the kurtosis of the normal distribution. Therefore, to visualize the parameter space, it is convenient to use the anti-kurtosis that is given as

$\kappa =\frac{1}{\sqrt{Ex+3}}$ ( 13 )

The use of anti-kurtosis makes possible to place all models of beta distributions of the second kind on a limited range of values, that is limited by the range from 0 to 0.6. Since the beta distribution models include symmetrical shapes, the third standard moment is used to set the model skewness parameter.

Entropy Coefficient of Non-Shifted beta-Distributions of Second Kind

In the entropy coefficient of the non-shifted distribution is proposed as an information feature for estimating the shape of distributions, that is given as (Polosin, 2020a; Polosin, 2020b).

$k_{Hn}=\frac{{\mathrm{\Delta }}_{Hn}}{\sqrt{m_{\mathrm{2}}}}$ ( 14 )

Where is entropy interval of uncertainty of non-shifted distribution,₂ is the initial moment of the second order.

The entropy coefficient for the non-shifted beta distribution of the second kind is given as

$K_{HnB\mathrm{I}\mathrm{I}}(u,v)=\sqrt{\frac{(v-\mathrm{1})\cdot (v-\mathrm{2})}{\sqrt{u\cdot (u+\mathrm{1})}}}\cdot B(u,v)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left[\right(\mathrm{1}-u\left)\psi \right(u)-(\mathrm{1}+v\left)\psi \right(v)+(v+u\left)\psi \right(u+v\left)\right]$ ( 15 )

Since the second initial moment of the beta distribution of the second kind imposes a restriction on the range of change of the second shape parameter from two to infinity, then this restriction is also imposed on the entropy coefficient of the non-shifted beta distribution of the second kind. It should be noted that this limitation is lower than for space of skewness and anti-kurtosis. Therefore, when constructing entropy-parametric spaces, the order of the standardized moment imposes the restriction on the range of the second shape parameter.

Space of Anti-Kurtosis and Entropy Coefficient

Figure 1 illustrates the features of the possible locations for models of beta distribution of the second kind in the space of the entropy coefficient and anti-kurtosis, where the following notation is used. The numbers of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11 are the trajectories of possible models of the beta distribution of the second kind for various ratios of the second shape parameter to the first parameter, that it is respectively equal to 0.001, 0.1, 0.5, 1, 2, 3, 5, 10, 20, 100 and 400. Attention should be paid to trajectories of 1 and 11, which are shown by a dotted line. These trajectories are the boundaries of the surface of possible positions of the beta distribution models. The numbers of 12, 13, 14, 15, and 16 are curves of the equivalent values of the second shape parameter that is respectively equal to 4.1, 5, 7, 10, and 120. The numbers of 17, 18, 19, 20 and 21 are curves of the equivalent values of the first shape parameter that is respectively equal to 0.2, 0.5, 1, 2 and 7.

See Full Size >

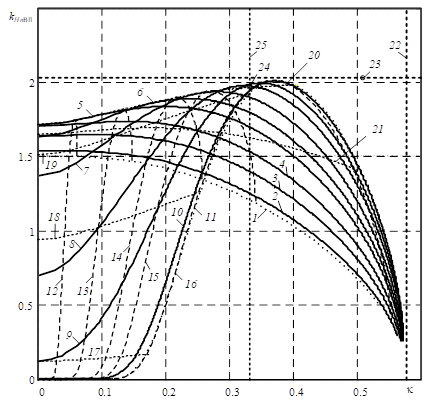
Figure 1 also shows the positions of the mesokurtic distributions with dashed line 22, where the anti-kurtosis is 0.577. The dashed line 25 defines the cutting plane for model that anti-kurtosis is 0.333. This corresponds to the anti-kurtosis of exponential distributions. The position of the asymmetric distribution of the modulus of the normal value is shown by the point with the number 23.

For this point, the anti-kurtosis and the entropy coefficient are 0.508 and 2.066, respectively. The position of the exponential distribution is illustrated by point 24 with the anti-kurtosis and the entropy coefficient that are 0.333 and 1.922, respectively.

The family of beta distributions of the second kind contains a distribution for which the entropy coefficient and the anti-kurtosis are equal to the corresponding characteristics of the exponential distribution, the position of which is given by point 24. If the first shape parameter is greater than 1 and the range of the second parameter is from 4 to 7, then the anti-kurtosis of the beta distribution of the second kind is less than the anti-kurtosis of the exponential distribution.

The beta distribution of the second kind contains a set of shapes for which the anti-kurtosis is greater than the anti-kurtosis of the exponential distribution, provided that the first shape parameter is greater than 1.5 and the second shape parameter is greater than 7.

Due to the restrictions imposed on the second shape parameter by the standardized moment of the fourth order, there are no models of the beta distribution of the second kind in the space, provided that the second shape parameter is less than 4. This significantly reduces the significance of the space of anti-kurtosis and skewness when this is used to analyse or preliminary estimate the parameters of the beta distribution second kind.

At the same time, the analysis in the space of the entropy coefficient and anti-kurtosis is more informative than in the space of anti-kurtosis and asymmetry. In particular, it follows from consideration of the space of the entropy coefficient and the counter-kurtosis that the family of beta distributions of the second kind does not contain distributions with shapes close to mesokurtic distributions. Wherein, a high value of the entropy coefficient allows you to set additional restrictions on the trajectories of distributions.

Space Based on Skewness and Entropy Coefficient

Figure 2 illustrates the possible positions for models of the beta distribution of the second kind in the space of the asymmetry and the entropy coefficient that it is given by trajectories and curves of the equivalent values of the shape parameter. Figure 2 retains the designations previously used to describe Figure 1 for trajectories and for curves of equivalent values of both the first and second parameters. The dotted plot 22 illustrates the position of the models, the skewness of which is equal to the distribution skewness of the normal value modulus.

Points 23 and 24 correspond to the position of the distributions of the modulus of the normal value and the exponential distribution with asymmetries equal to 0.9953 and 2, respectively. Point 23 in Figures 1 and 3 is outside the surface of possible patterns of beta distribution of the second kind.

See Full Size >

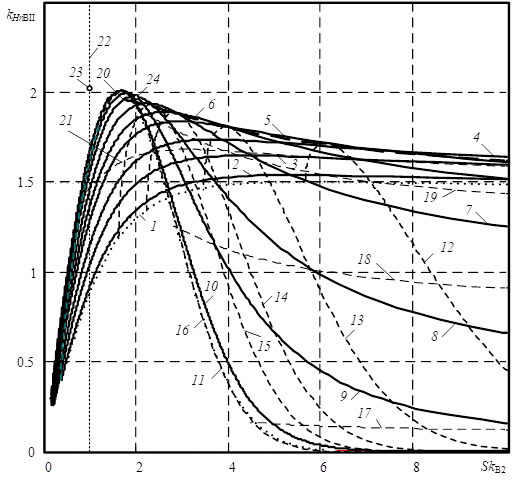
Obviously, among the models of the beta distribution of the second kind, there are no models whose shape corresponds to the shape of the distribution of the normal value modulus that is given as point 23 in Figure 1 and 2 near the surface of possible models. It can be assumed that the distribution of the second kind contains the shape set close to exponential distribution, provided that the first shape parameter is equal to 1.5, the second shape parameter is more than 10.