Automation Of The Process Of Teaching Students To Solve Computational Problems

Abstract

Learning to solve computational problems both at school and at the university is the most important component of the educational process in any exact discipline. In the context of the digital transformation of education, the issues of automating the process of organizing personalized independent work of students to solve problems are becoming relevant. In this regard, the work aimed to substantiate and experimentally test an approach to formalizing the process of teaching students to solve computational problems. The main idea of the research is to create an automated interactive software environment developed based on structural and mental schemes and the "white box" model. To increase the effectiveness of independent learning using this environment, elements of gamification are used, visualization of the dynamics of the formation of the ability to solve problems using the forgetting factor and the A. Elo rating. Experimental testing of the created tool in the real educational process allowed us to evaluate the effectiveness and advantages of the proposed approach to automating the process of teaching students to solve computational problems. The use of problem-based structural-mental schemes allows you to create software training tools for many subject areas. The materials of the article are of interest to researchers in the field of the use of artificial intelligence in education.

Keywords: Learning to solve computational problems, structural-mental schemes, computational primitives, "white box" model

Introduction

Solving problems in teaching any discipline is one of the main types of educational activity of the student. The initial foundation of the ability to solve problems is laid in childhood, then when receiving a general education at school. In the future, this skill becomes necessary for studying technical disciplines in technical schools and universities in various areas, specialties and professions.

However, it should be recognized that the level of problem-solving skills of students remains quite low, despite its importance. This is confirmed by the facts of real school practice. For example, the results of the Unified State Exam in exact disciplines show a drop in the level of this skill in recent years (Unified State Exam portal, 2020). The problem under consideration determines the low readiness of students to study at the university. Especially this situation is the cause of serious difficulties in the effectiveness of teaching students special technical disciplines in educational institutions of secondary vocational education.

The ability to solve problems for a person is deeply individual, and personification in its formation becomes a key factor in the success of the training. The formation of the ability to solve problems is provided effectively to a greater extent with the independent work of the student.

In this regard, the issues of formalization and automation of the process of organizing personalized independent work of students when learning to solve computational problems are relevant.

Problem Statement

Increasing the role of independence in students' learning activities makes it important to create methods for their personalized learning to solve problems. It is very problematic to organize such independent work of students with a class-based system due to its high labor intensity and large organizational and time labor costs. The need to resolve this contradiction determines the relevance of the study and determines its problem: how to automate the process of organizing personalized independent work of students to solve problems?

The leading idea of the research is the assumption that the automation of the process of organizing personalized independent work of students will be effectively provided if you use automated software tools in which:

• the formalization of the process of teaching students to solve problems is carried out using subject structural and mental schemes, and the training and control of this skill is implemented based on the "white box" model;
• the adaptability of the selection of tasks in terms of complexity is provided by the Elo rating; the internal motivation of students to work independently on solving computational problems is formed using game mechanics and taking into account forgetting according to the piecewise linear law.

Research Questions

• To formalize the process of teaching students to solve computational problems based on structural and mental schemes.
• Develop a set of subject structural and mental schemes that formalize the ability to solve computational problems (using the example of physical problems).
• Develop an interactive software environment that allows you to automate the process of organizing personalized independent work of students to solve problems.
• To evaluate the effectiveness of the approach to automating the process of organizing personalized independent work of students on learning to solve computational problems (for example, physical problems).

Purpose of the Study

The purpose of the work is to theoretically substantiate the possibility of automating the process of organizing personalized independent work of students of the technical profile of secondary professional institutions to solve problems and develop a trial interactive software environment on the platform of structural and mental schemes and the "white box" model, which ensures the effectiveness of the formation of students ' ability to solve computational problems. At the same time, it is necessary to provide for the use of artificial intelligence elements at all stages of training.

Research Methods

In the course of the research, the following methods were used:

• the study and analysis of scientific, methodological and psychological-pedagogical literature on the research problem and related areas;
• analysis of federal state educational standards of secondary general and secondary vocational education of various technical specialties and professions;
• empirical methods: testing, observation, experiment;
• nonparametric methods of statistical processing of experimental data: comparison of dependent samples (Wilcoxon T-test); comparison of independent samples (Mann-Whitney U-test).

The theoretical and methodological basis of the study is:

• the system-activity approach and the theory of developmental learning (Wiener, 1983);
• task-based approach in teaching and private subject teaching methods (Ball, 1990; Usova & Tulkibaeva, 2001);
• research in the field of informatization of education (Bazhenova et al., 2016; Grigoriev et al., 2009; Zakharova et al., 2017);
• research in the field of cognitive psychology and the cognitive approach in education (Anderson, 2002; Galperin & Zhdan, 1992; Neisser, 1981);
• research in the field of cybernetics (Ashby, 1959; Wiener, 1983).

Findings

Let's consider a generalized model of automation of the student's self-learning process (Figure 1). In the block of recognition of the didactic state of the student, the characteristics of the personality are set in the form of an information vector (x₁,…,x_n) and giving them weights (z₁,…,z_n). After the expert determines the clustering features, the classes of trainees are formed: Q₁,...,Q_k. For example, let x1 – solving a test problem 1, z₁ = 0…1 (simple task): x2 - solution of the test problem 2, z₂ = 0…3 (challenging task); x₃ – solving a test problem 3, z₃ = 0…5 (super-difficult task). Assigns for clustering, we will take 4 levels of readiness of the student: Q₁ - over-programming level; Q₂ – program level; Q₃ – basic level; Q₄ – entry-level. The procedure for recognizing a user is to determine whether it belongs to a certain class Q_i by submitting test tasks. The content block includes a set of educational elements that are diverse in terms of pedagogical design. For example, the case described above contains four concentric content modules corresponding to the given levels of student readiness. The section with training in problem-solving requires separate consideration, which is what the study of this work is devoted to.

See Full Size >

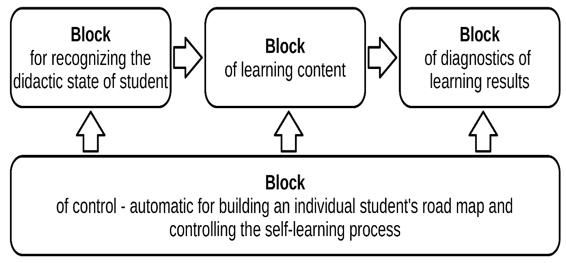
The diagnostic block has a classic character, including different methods of evaluating learning outcomes.

The control module creates an individual learning roadmap of the student, based on the recognition of his didactic state, and organizes the process of interactive interaction of the user with a block of meaningful learning elements.

Due to the importance of the process of teaching students to solve problems, we will consider this section in an online project (Asaulenko, 2020), which is a web application adapted for mobile devices and available on the Internet.

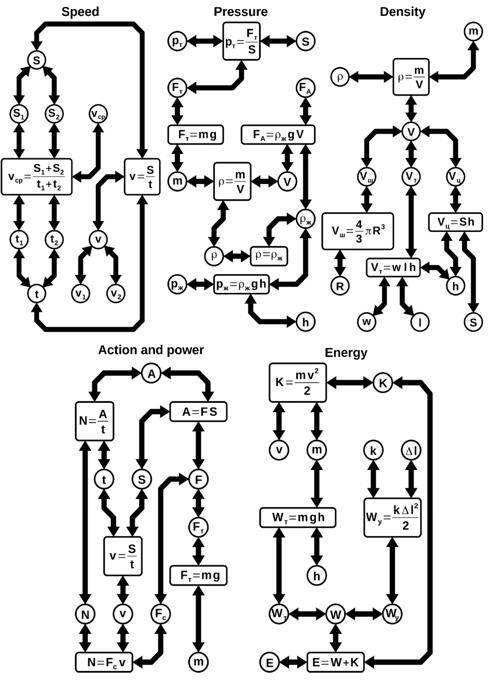
To ensure the possibility of automating the process of organizing independent work on solving problems, it was necessary to develop a way to formalize this skill. For this purpose, the concept of a computational primitive was introduced, which represents a graph whose central node is connected to a mathematical model of a certain process or object, and the peripheral nodes represent the quantities included in this model.

Such a graph allows you to model elementary calculation operations for calculating one of the values from the known others.

The scheme, composed by a superposition of several such primitives, represents a structural-mental scheme, samples of which are shown in Figure 2.

See Full Size >

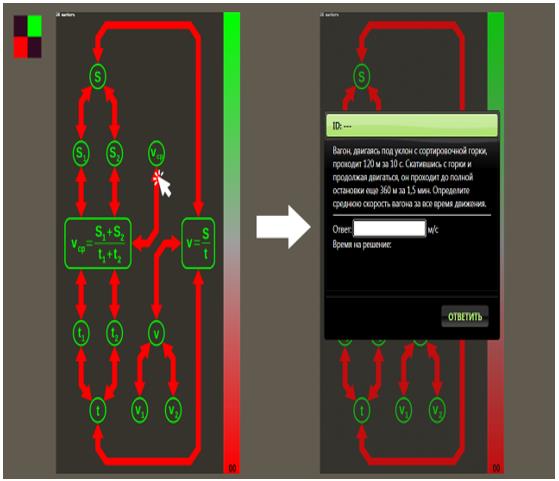
On the platform of these schemes, a promo version of the software environment was developed, the interface of which is shown in Figure 3.

See Full Size >

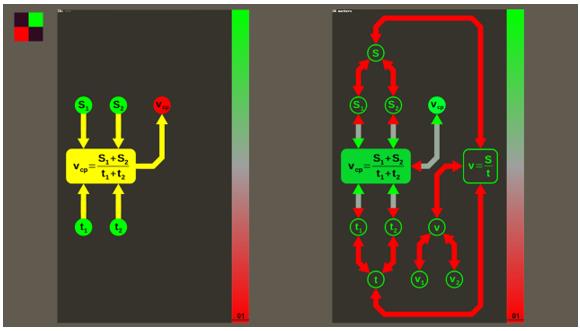
In the developed software environment, each link of the structural mental scheme has a weight that is initially zero, and the link is shown in red, as in the left image of Figure 4. They are active, when the mouse "clicks" on the arrow indicating the link, the system offers the user a task, the solution of which contains an operation corresponding to this link.

If the problem is solved correctly, then the links that are included in its solution are colored green, and their weight becomes the maximum, equal to 100.

See Full Size >

Thus, in the learning process, a didactic model of the student is formed in the form of a set of characteristics of the connections of the structural and mental scheme. The "white box" model used allows us to judge by its state what operations have been worked out in solving problems on this topic, taking into account the time factor.

To ensure the automation of individual selection of tasks for the student, the Elo rating system was used (Pelanek, 2016).

Adapted for didactic purposes, this system has the following form. Both students and tasks are assigned coefficients-ratings. Their initial values should be large enough to avoid negative values when further adjustments are made (in this case, the value 1000 pt is assumed). The ratings are recalculated after each attempt to solve the problem. If the student solves the problem correctly, then his rating increases and the rating of the problem decreases, in the opposite case, the rating of the problem increases, and the student decreases. The mathematical expectation of the result of solving the problem for the student is determined by the following formula

$M_S=\frac{\mathrm{1}}{\mathrm{1}+e^{-\lambda \left(R_S-R_T\right)}}$ ,

where $M_S$ – a mathematical expectation of the result of solving the problem for the student; $R_S$ – current student rating; $R_T$ – current task rating. Coefficient $\lambda$ accepted as equal 7,327·10^-3. Similarly, the mathematical expectation of the result of solving the problem for the problem is determined $M_T$, which is related to $M_S$ by the following ratio:

$M_T=\mathrm{1}-\mathrm{}{M}_S$.

The rules for adjusting ratings are as follows:

$R_S^{new}=\mathrm{}{R}_S+K_S\left({\delta }_S-M_S\right)$,

$R_T^{new}=\mathrm{}{R}_T+K_T({\delta }_T-M_T)$,

where $R_S^{new}$ – new student rating; $K_S$ – a scale of student rating increments; $R_T^{new}$ – new task rating; $K_T$ – a scale of task rating increments; ${\delta }_T$ – the result of solving the problem relative to the problem (0 – problem solved correctly, 1 – a problem not solved); ${\delta }_S$ – the result of solving the problem concerning the student (1 – problem solved correctly, 0 – mistake). the ratio is also true:

${\delta }_T=\mathrm{1}-\mathrm{}{\delta }_S$.

Value $K_S$ is equal to 100 for each user when solving the first 20 tasks, after that it is equal to 20.

To prove a sufficient degree of adaptability provided by the use of the A. Elo rating system, the frequency of correct solutions to problems was studied, depending on the difference in the ratings of the student and the problem. After a long-term application of the developed system, a graph of this dependence was constructed, which is shown in Figure 5. This graph shows the number of decisions based on the results of which the frequency was calculated.

See Full Size >

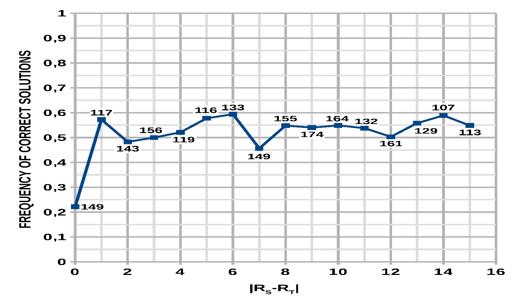
As can be seen from the figure, with a rating difference of several points, the frequency of correct decisions is close to 0.5, that is, the problem closest to the rating can either be solved or not solved with equal probability. Therefore, the use of the Elo rating allows you to organize an adaptive automated selection of tasks.

In the software environment, an algorithm is implemented, according to which the weight of each connection of the structural mental scheme decreases with time due to the effect of forgetting. A piecewise linear function was used as the law of forgetting, and the amount of information stored in memory can be calculated using the formula:

$\kappa =\mathrm{}\mathrm{100}-\mu (\tau -t)$,

where: $\kappa$ – the amount of information stored in memory (the weight of the connection on the SMS); $\mu$ – speed of forgetting; $\tau$ – time, elapsed since the last repetition; $t$ – time elapsed after the first memorization. With each repeated solution of the problem, the weights of the links that are included in its solution increase to the maximum. At the same time, the rate of forgetting them decreases. An approximate view of which is shown in Figure 6.

See Full Size >

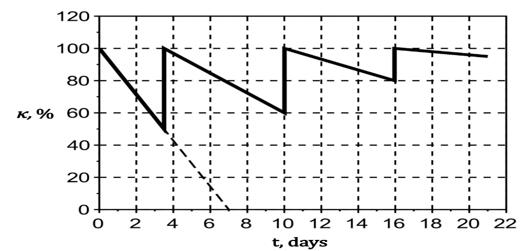
The accepted method of accounting for forgetting allowed us to introduce a characteristic of the formation of the ability to solve problems both in terms of the completeness of this skill and in terms of its strength. This characteristic was called the level of assimilation. The level of assimilation of the topic L for solving problems is determined by the product of the average value of the link weights by a coefficient that depends on the average rate of forgetting according to the following formula

$L=l·\stackrel{-}{\kappa }$,

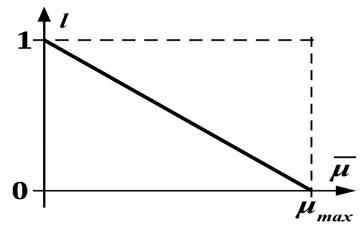
where: $\stackrel{-}{\kappa }$ – arithmetic mean of the weights of the SMS links (completeness characteristic); $l$ – a multiplier that is a strong characteristic. The value of l is defined by the expression:

$l=\mathrm{}\left(\mathrm{1}-\frac{\stackrel{-}{\mu }}{{\mu }_{max}}\right),$

where: $\stackrel{-}{\mu }$ – arithmetic means of link forgetting rates SMS; ${\mu }_{max}$ – a maximum (initial) value of the forgetting rate. In the developed system, the value is 14.3. With this value, the information learned for the first time will be forgotten in a week. This value made it possible to motivate students to fairly frequent periodic repetitions of the educational material. The graph of the dependence of the value of l on the average value of the rates of forgetting elements of the structural mental scheme is shown in Figure 7.

See Full Size >

Determined by the described formulas, the value of L will vary from 0-in the complete absence of worked-out connections to 100-with all the worked-out connections of the structural and mental scheme and at the same time a fairly low rate of forgetting them. The sum of such values for all topics is called the integral level of assimilation. Undoubtedly, this value is related to the student's ability to solve problems.

In this regard, it is of interest to study the correlation between the integral level of assimilation achieved by students at the end of the pedagogical experiment and the number of tasks solved in the output test.

See Full Size >

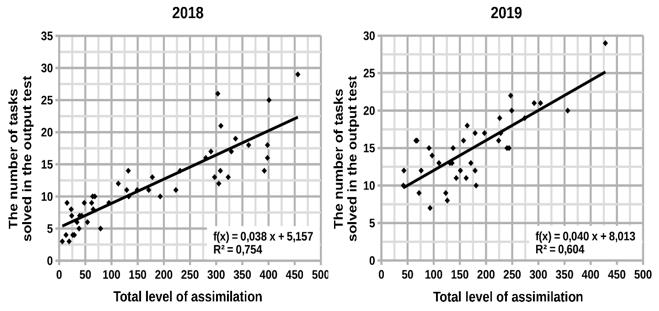
The scattering diagrams of these values for experiments of different years are shown in Figure 8. The approximate value of the linear correlation coefficient for the first graph turned out to be 0.9, – for the second 0.8. Therefore, we can state a close relationship between these values.

To form and maintain the motivation of students to work in the software environment, gamification elements are implemented, in the form of some game mechanics. Game mechanics is a way of organizing the student's interaction with an interactive software environment, the main purpose of which is to increase motivation through the distribution of some virtual asset. The following game mechanics were used: Achievement, Dynamic Assignment, Pride, Avoidance, and Envy (Schonfeld, 2020).

In the pedagogical experiment, it was revealed that the students of the experimental group not only solved on average a larger number of tasks but also achieved high values of game mechanics. This indicates a high motivation of students to work with the software environment.

See Full Size >

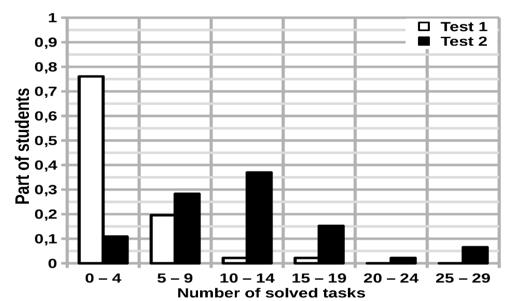
To study the effectiveness of the program environment in 2018, the first pedagogical experiment was conducted, in which a group of students took part. Before working with the software environment, input testing was performed. After the students had worked with the software environment for 6 weeks, an exit test was conducted.

The distribution of students by the number of solved problems is shown in Figure 9.

The histogram shows that after working with the system, the proportion of students who solved more problems increased. Since the samples, in this case, are dependent, the Wilcoxon T test was used to prove the statistical significance of the differences. Its value fell into the zone of significance.

See Full Size >

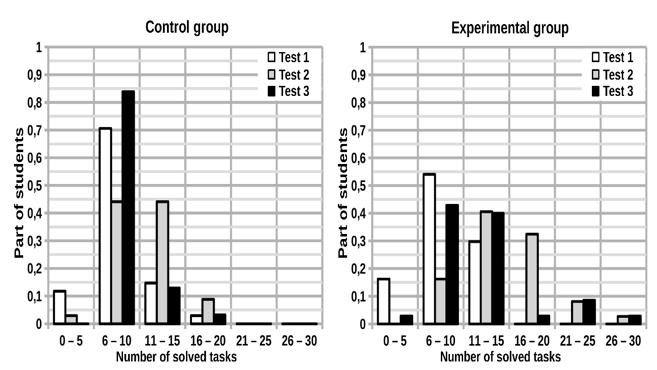
To strengthen the fact of the effectiveness of training when using the software environment, a second experiment was conducted in 2019, during which the results of training in two groups of trainees were analyzed. In the control group, independent work was organized traditionally.

In the experimental group, a software environment was used. Before starting the experiment, an input test was performed.

Six weeks later, an exit test was conducted, and two months later, a control test was conducted, the purpose of which was to determine the residual effect of the independent work done.

The distribution of students in the control and experimental groups by the number of tasks solved in the given tests is shown in Figure 10.

See Full Size >

Figure 11 shows the average number of tasks solved by students in the experiments of 2019. Since the samples are independent in this case, the Mann Whitney U test was used to prove the statistical significance of the differences. The values of this criterion for both the output test and the control test fell into the zone of significance. Thus, the effect of the effectiveness of students 'learning when using the developed software environment turned out to be both greater and longer in comparison with the results of students' learning with the traditional method of organizing independent work.

Conclusion

The conducted experiments confirm the scientific hypothesis about the possibility of automating the process of organizing students ' independent work on solving computational problems and show the high effectiveness of the experimental software environment developed on the platform of structural-mental schemes for solving problems in the subject area.

The novelty of the research results lies in the fact that the idea of the possibility of automating the process of organizing students ' independent work on solving computational problems is proposed and implemented in practice due to the formalization of this skill with the help of structural and mental schemes and the organization of control according to the "white box" model.

The results of the study allow us to draw the following conclusions:

1. Structural-mental schemes of the subject area, built with the help of computational primitives, allow you to formalize the ability to solve computational problems.

2. Automation of the process of organizing personalized independent work of students to solve computational problems is fundamentally possible when using:

• Elo rating to ensure the adaptability of the system;
• game mechanics to ensure students ' motivation;
• a piecewise linear model of forgetting for a time-dynamic assessment of the level of formation of the ability to solve computational problems;
• "white box" models for organizing control.

3. The automated interactive software environment developed according to the proposed approach ensures the effectiveness of students ' independent work on solving computational problems.

The proposed model of automation of self-study of students can be applied to many subject areas. The materials of the article are of interest to subject teachers of schools, teachers of secondary vocational schools and universities, as well as researchers in the field of the use of artificial intelligence in education.

Acknowledgments

This study was carried out within the framework of the International Program of Scientific Grants for Conducting Research based on the Institute for Advanced Studies of the Moscow Pedagogical State University (Moscow, Russia), as well as project № 2021012106985 «Formation and development of computational thinking of students on the basis of automated and cognitive teaching tools» was supported by Krasnoyarsk Regional Fund of Science (Krasnoyarsk, Russia).

References

• Anderson, J. R. (2002). Cognitive psychology. Series «Masters of psychology». SPb. Peter.

• Asaulenko, E. V. (2020). Automation of the process of formation of students ' ability to solve computational problems from the standpoint of the cognitive approach. [Master’s thesis] Siberian Federal University.

• Ashby, W. R. (1959). Introduction to cybernetics. Publishing House of Foreign Literature.

• Ball, G. A. (1990). Theory of educational tasks: Psychological and pedagogical aspect. Pedagogika.

• Bazhenova, I. V., Babich, N., & Pak, N. I. (2016). From projective-recursive learning technology to mental didactics. Sib. feder. un-t.

• Galperin, P. Ya., & Zhdan, A. N. (1992). History of psychology. The period of open crisis (early 10s-mid 30s of the XX century). Publishing House of Moscow. un-ta.

• Grigoriev, S. G., Grinshkun, V. V., Zaslavskaya, O. Yu., Kulagin, V. P., & Belyaeva, N. I. (2009). Monitoring the use of informatization tools in the Russian secondary education system. Bulletin of RUDN University of Russia. Series "Informatization of education".

• Neisser, W. (1981). Cognition and reality. The meaning and principles of cognitive psychology. Progress.

• Pelanek, R. (2016). Applications of the Elo Rating System in Adaptive Educational Systems. Computers & Education.

  Google Scholar

  Crossref

• Schonfeld, E. (2020). SCVNGR's Secret Game Mechanics Playdeck. Retrieved 24 May, 2020 from https://techcrunch.com/2010/08/25/scvngr-game-mechanics/

• Unified State Exam portal. (2020). Average scores of the Unified State Exam-2019. Retrieved 24 May, 2020, from https://4ege.ru/ege-gia/58093-srednie-bally-ege-2019.html

• Usova, A. V., & Tulkibaeva, N. N. (2001). Practicum on solving physical problems: For students of Physics and Mathematics. Prosveshchenie.

• Wiener, N. (1983). Cybernetics, or control and communication in the animal and the machine. Nauka.

• Zakharova, I. G., Lapchik, M. P., Pak, N. I., Ragulina, M. I., Timkin, S. L., Udalov, S. R., Fedorova, G. A., & Henner, E. K. (2017). Modern problems of informatization of education. OmSPU.