The Population Health And The Environment Quality: Construction Of Mathematical Assessments

The population health level assessment. Analysis of statistical material

We solve the problem of assessing the population health level on the example of the Udmurt Republic (UR). In accordance with the division of the population by health condition, we examine the statistical information provided on the official statistical sites of the Russian Federation. We use the methods of statistical processing of the official information available to the researcher.

Figure 1 shows the region’s population dynamics for the period 2000-2020.

See Full Size >

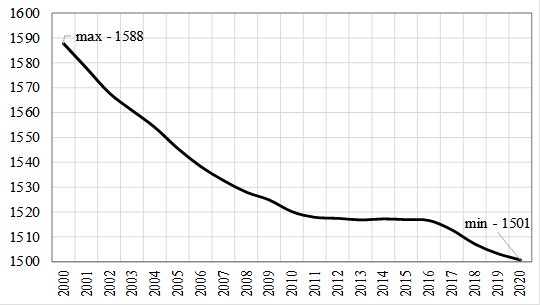
Figure 2 presents statistical data on the general and primary morbidity per 1000 people of the UR’s population for the period 2000-2020.

See Full Size >

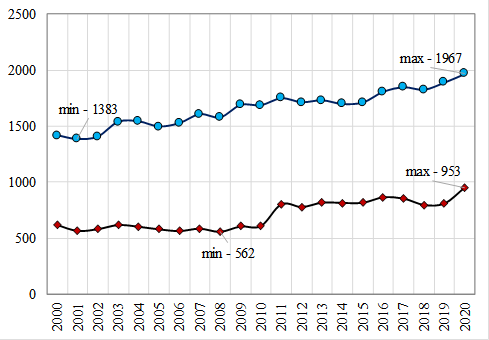
According to the medical classification, the primary morbidity is a set of newly emerging diseases that have not been accounted for anywhere and for the first time in a given year among the population (relapses of chronic diseases that occur during the year are not taken into account); the total morbidity is the sum of primary diseases and diseases accumulated in previous years, i.e. known in advance. Thus, the total morbidity characterizes the total number of existing diseases among the population of a given territory during a certain period of time.

The general morbidity of the UR’s population for the period 2000-2020 increased by 38.8% and amounted to 1967 diseases per 1000 people. For the entire regional system, in terms of the total population, the incidence changed from a value of 2250.8 to a value of 2952.5 thousand diseases.

The primary morbidity of the UR’s population for the period 2000-2020 increased by 53.2% (compared to the beginning of the studied period in 2000) and amounted to 953 diseases per 1000 people. For the entire socio-economic system of the region, in terms of the entire population, the primary incidence rate changed from 987.3 to 1430.4 thousand diseases.

Since the general morbidity is the sum of primary and existing diseases, then, consequently, the increase in the total morbidity of the UR’s population for the period 2000-2020 is conditioned by the presence of newly diagnosed diseases. This situation is partly due to the introduction in the Russian Federation since 2011 of regular medical examinations, which significantly increased the detection rate of primary diseases among the population.

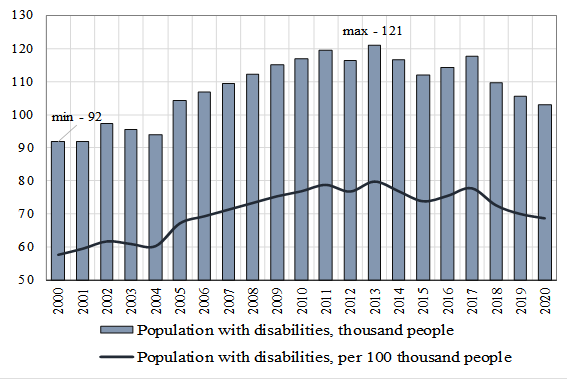
For health condition, the population of the regional socio-economic system is grouped as follows: a healthy individual; having chronic diseases; having a disability. Figure 3 shows the dynamics of people with disabilities (the graph is based on statistical data), as well as the calculated values of people with disabilities per 100,000 people of the UR for the period 2000-2020.

The population with disabilities in the region increased from 92.0 to 103.2 thousand people for the period 2000-2020, the growth rate is 12.2%. People with disabilities (per 100 thousand of the population) in the region grown up from 57.8‰ to 68.7‰ (for comparison, in 2020 it is 75.1‰ for the Russian Federation).

See Full Size >

The group of people with disabilities is also characterized by an internal division according to the degree of disability. The third group of disability presupposes a person's ability to work; the second group is established when a person is partially capable of labor activity; the first group of disability occurs when a person is completely incapable of work.

The change in the internal structure of the studied population category in the UR according to the disability degree is shown in Figure 4.

See Full Size >

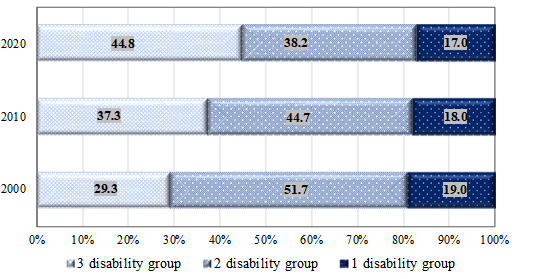
Redistribution takes place between groups. The proportion of people able to work is increasing. Over the period 2000-2020, the increase in people able to work is 2 percentage points.

The assessment of the environmental quality and the effectiveness of environmental protection measures

We construct a model of the environmental factor dynamics and the effectiveness of environmental protection measures using the methods of economic and mathematical modelling. As noted in the introduction, an important factor influencing the population health level is the environmental factor. As a result of human activity, the natural environment changes: atmospheric air, water resources and land resources are polluted. The environment is a collection of three types of resources: atmospheric air, water and soil. Therefore, the ecological factor reflects the change in all three explicit components of the environmental components (implicit, that is, indirect objects of the influence of human life are, in particular, living organisms). The values of the environmental factor ${\mathrm{\Omega }}_{\mathrm{i}}={\mathrm{\Omega }}_i\left(t\right)$ is measured as a percentage, calculated as a part of the unpolluted natural resource in its total volume. We also introduce the concept of a measure of environmental pollution, which determines the degree of deterioration of the environmental factor. We divide the environmental factor by type of costs aimed at environmental protection and rational using of natural resources: investments protecting atmospheric air, water resources and land resources. The total value of the environmental factor is defined as a linear combination: $\begin{array}{c}\mathrm{\Omega }\left(t\right)={\alpha }_1{\mathrm{\Omega }}_1\left(t\right)+{\alpha }_2{\mathrm{\Omega }}_2\left(t\right)+{\alpha }_3{\mathrm{\Omega }}_3\left(t\right),\end{array}$ (1)

${\alpha }_i\in \left(\mathrm{0,1}\right);\underset{i=1}{\overset{3}{\sum }} {\alpha }_i=1.$ (2)

In formulas (1) and (2) ${\alpha }_i$ is the share of the corresponding terms in the total volume factor; index i=1 defines atmospheric air, i=2 – water resources, i=3– land resources.

The dynamics of the i-th component of the environmental factor is determined by an ordinary differential equation of the first order:

$\stackrel{\dot{}}{{\mathrm{\Omega }}_{\mathrm{i}}=Z_i{k}_i-{\eta }_i\left(t\right){\mathrm{\Omega }}_i.}$ (3)

In formulas (3) $Z_i$ is the sum of the costs of carrying out clean-up measures and environmental protection for the i-th component of the environmental factor; $k_i-$the coefficient of conversion of the costs expressed in monetary units into units of measurement of the environmental factor; ${\eta }_i\left(t\right)$-the intensity of pollution i-th component of the environmental factor.

The initial condition of the i-th environmental factor component at $t=t_0$ has the form:

${\mathrm{\Omega }}_i\left(t_0\right)=Z_i\left(t_0\right)k_i$, (4)

where $Z_i\left(t_0\right)$ -the value known from the statistical data.

The dynamics equation (3) with the initial data (4) is a Cauchy problem. The solution is carried out by a numerical three-stage Runge-Kutta method of 3 orders. For the variable t we introduce a difference grid with a step h and consider the set of points $t_n=nh,n=0,1,2,\dots$Then the calculation formulas take the form:

$\begin{array}{c}{\mathrm{\Omega }}_i^{n+1}={\mathrm{\Omega }}_i^n+\frac{h}{6}\left(F_i^1+4F_i^2+F_i^3\right),F_i^1=Z{\left(t_n\right)}_i{k}_i\left(t_n\right)-{\eta }_i\left(t_n\right){\mathrm{\Omega }}_i^n\\ F_i^2=Z{\left(t_n\right)}_i{k}_i\left(t_n\right)-{\eta }_i\left(t_n\right)\left({\mathrm{\Omega }}_i^n+\frac{h}{2}{F}_i^1\right),F_i^3=Z_i\left(t_n\right)k_i\left(t_n\right)-{\eta }_i\left(t_n\right)\left({\mathrm{\Omega }}_i^n-h{F}_i^1+2h{F}_i^2\right)\end{array}$(5)

The effectiveness of environmental protection measures (indicate it $\varphi =\varphi \left(t\right)$) it directly affects the value of the environmental factor $\mathrm{\Omega }\left(t\right)$. We analyze this indicator. The effectiveness of environmental protection measures is inversely proportional to the intensity of environmental pollution $\eta =\eta \left(t\right)$ with a certain coefficient a. Then, for the i-th resource, has the relation:

${\varphi }_i=\frac{a_i}{{\eta }_i}$. (7)

We determine the intensity of environmental pollution by expressing it from the formula (3):

${\eta }_i=\frac{k_i{Z}_i-\stackrel{\dot{}}{{\mathrm{\Omega }}_{\mathrm{i}}}}{{\mathrm{\Omega }}_i},$ (8)

We determine the coefficient of conversion k of the amount of costs for environmental protection measures expressed in monetary units into units of measurement of the environmental factor. To do this, we calculate the ratio of the volume of the cleared resource U of the i-th type to the current cost of protecting this resourceZ, the index j sets the time period, year:

${\zeta }_i^j\left(t\right)=\frac{U_i^j\left(t\right)}{Z_i^j\left(t\right)},i=\stackrel{-}{\mathrm{1,3}}$. (9)

Next, it should calculate the values of the coefficients of the conversion of the environmental factor components into monetary terms, as the ratio of the average value for the period $\stackrel{-}{{\zeta }_i}\left(t\right)$ to the known values of the total volume of these resources.

Results of the structural and dynamic analysis of the population health level in the region

As noted above, according to the health condition, the population of the regional socio-economic system are grouped as follows: a healthy individual; having chronic diseases; having a disability. The total population of the region denote as P; the healthy people is $P_H$; the people with chronic diseases is $P_{CH}$; the disabled people is $P_{INV}$. Based on the data presented in the graphs of Figures 1-3, the number of healthy population per year can be determined by the formula:

$P_H\left(t\right)=P\left(t\right)-P_{CH}\left(t\right)-P_{INV}\left(t\right)$. (10)

As a result, the distribution of healthy people from the working-age group in the UR region for the period 2000-2020 is obtained, the graph of which is shown in Figure 5.

See Full Size >

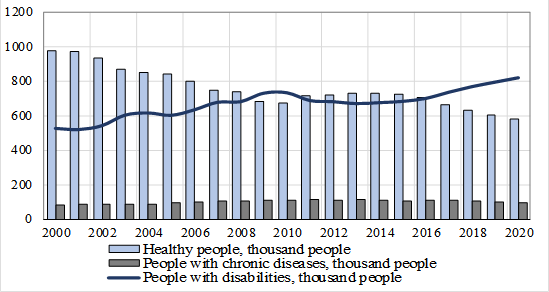
The graph has a wave-like character, since the health level is related to the age characteristics of the population, which change in a wave-like manner (see Figure 6).

See Full Size >

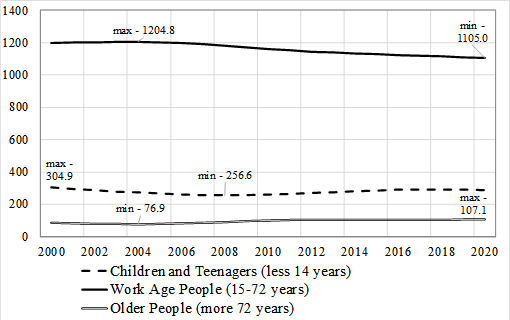
Figure 7 shows the changes diagram in the population health level of the UR in the division into three groups (healthy people, people with chronic diseases and people with disabilities).

See Full Size >

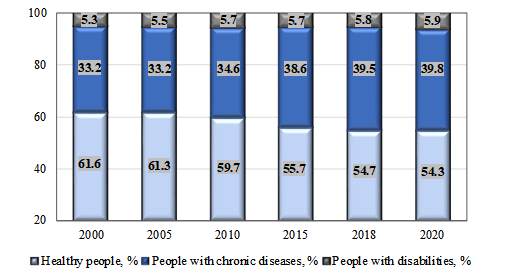
As a result of the structural-dynamic analysis of the population health level of the Udmurt Republic for the period 2000-2020, it is found that the share of healthy people decreased from 61.6% in 2000 to 54.3% in 2020 (the overall rate of decline for the period is 11.8%, the annual rate is 0.6%); the share of people with chronic diseases increased: 33.2% in 2000 to 39.8% in 2020 (the overall growth rate for the period is 19.9%, the annual growth rate is 0.9%).

Numerical results of assessment the effectiveness of environmental protection measures in the region

The value of the environmental factor $\mathrm{\Omega }$ directly depends on the effectiveness of environmental protection measures. Dynamics of the environmental factor in three components (atmospheric air, water resources and land resources) for the UR for the period 1996-2020 are presented in Figure 8. Figure 9 shows the environmental factor dynamics by three components as the dynamics of the annual rates of environmental pollution in the region.

See Full Size >

See Full Size >

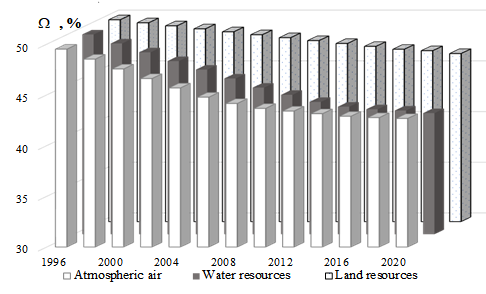
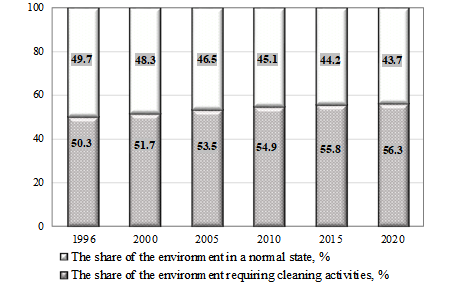
As a result of calculations, it is found that the average annual rate of pollution in the UR of atmospheric air is 0.64%, water resources – 0.73%, land resources – 0.31% (Figure 8). The annual share of the environment, which requires the using of cleaning measures, on average for the period 1996-2020 for UR is 53.9%. Over the 25-year period under study, the share of the environment in need of treatment has increased from 50.3% to 56.3% (Figure 9). The most intense pollution is the atmosphere and the water. The soil is polluted less intensively, but, nevertheless, production and economic activities cause significant damage to nature, given the cumulative nature of this phenomenon.

The calculated dynamics of the environmental factor shows that the rate of pollution has decreased. This is due to the strengthening of measures aimed at combating environmental pollution in the last decade.

We determine the coefficient of conversion k of the value, expressed in monetary units, into the amount of refined resources. First, we calculate in accordance with formula (9) the average for the period 1996-2020 the value of the coefficient $\stackrel{-}{{\zeta }_i}\left(t\right)$ for each resource. For the calculation, we use information on the annual indicators of pollution and purification of atmospheric air, water and land resources of the UR for the period 1996-2020 and information on the current costs of environmental protection of the UR for the period 1996-2020 (in the calculations, the current financial costs for the possibility of comparing the obtained results were adjusted to 2020 prices). Average value of the coefficient $\stackrel{-}{{\zeta }_i}\left(t\right)$ for each resource: $\stackrel{-}{{\zeta }_1}=0.144,\stackrel{-}{{\zeta }_2}=0.021,\stackrel{-}{{\zeta }_3}=0.014.$

Further, the values of the coefficients for converting the components of the environmental factor into monetary terms are calculated, as a ratio $\stackrel{-}{{\zeta }_i}\left(t\right)$ to the known values of the total volume of these resources. Received the following values: $k_1=3.5\cdot {10}^{-6},k_2=3.4\cdot {10}^{-6},k_3=3.3\cdot {10}^{-6}.$

For the period under study, 1996-2020, according to the UR, there are calculated values obtained in accordance with formula (8), the values of the intensity of pollution for atmospheric air is ${\eta }_1=0.01\pm 0.00023$, pollution intensity for water resources is ${\eta }_2=0.003\pm 0.00006$ and for land resources is ${\eta }_3=0.01\pm 0.00057$.

Based on the values of the annual indicators of pollution and purification of atmospheric air, water and land resources of the UR for the period 1996-2020 and calculations of the intensity of environmental pollution, the values of the proportionality coefficients for the corresponding resources are obtained: $a_1=0.003,a_2=0.001,a_3=0.004.$

Thus, the estimated efficiency of environmental protection measures, determined by formula (7), for atmospheric air is about 25.0%, for water resources is 47.5%, for land resources is 38.0%.

Numerical results of assessment the relationship between the environment quality and the population health level

We consider aspects related to the assessment of the relationship between the environmental factor and the population health level of the social and economic system on the example of the UR. For this, we use the preliminary results presented in this work. We analyze the data shown in the diagrams in Figure 7 and Figure 8.

Let’s study the correlations between the dynamics of the percentage of the environment that does not need cleaning measures and the dynamics of the percentage of different population groups in the region in terms of their health status.

Table 1 shows the correlation coefficients calculated in accordance with the formula:

$r_i^j=\frac{cov\left(X_i,X_j\right)}{{\sigma }_{X_i}\cdot {\sigma }_{X_j}}$ (11)

Where $cov\left(X_i,X_j\right)$ -covariance between indicators $X_i$ and $X_j$; $\sigma$-standard deviation.

All correlation coefficients have values close to $\pm 1$. The significance level of the obtained coefficients is 99%.

So, the healthy population in the region directly depends on a clean ecology (94.4%). Obviously, the number of groups of people with health problems (general morbidity, chronic diseases, disability) shows an inverse relationship with the indicator of “clean” ecology. Thus, the general morbidity of the population depends on the poor quality of the environment by 95.8%, chronic morbidity – by 90.8%, disability to a lesser extent – by 83.7%.

The results of the correlation analysis, obtained when assessing the relationship between the population health level and the environment quality, taking into account the distribution of the population by age (dynamics of some age groups is shown in Figure 6), are presented in Table 2.

The results of this analysis are showed that environmental pollution has a negative effect on the health of all age groups; nevertheless, there is some cumulative effect, since the correlation coefficients slightly increase as a person grows up.