Interval Probabilities In Lpm For Risk Assessment In Socio-Economic Systems

Abstract

In the article the disadvantages of the logical and probabilistic method (LPM) for assessment risk and safety in socio-economic systems are described, namely, the assumption of the independence of events, "conjunction error", the subjectivity of experts in event tree construction. Proceed from properties of socio-economic systems, the author proposes to use interval estimations for probabilities of initiating events instead of point ones. Interval estimations allow avoid significant limitations in applying LPM for risk management in socio-economic systems which are caused by subjectivity of experts and “conjunction error”. The semantics of the formula for calculation the probabilities of events is determined by the rules of addition and multiplication of probabilities, and operations are performed according to the rules of interval mathematics. Examples of calculations of interval probabilities of events are given using numerical examples. The scientific foundation of the interval estimations of probabilities based on the axiomatics of the probability space and the space of events by A.N. Kolmogorov and sigma-algebra by E. Borel are stated.

Keywords: Interval probability, logic, risk, system, event

Introduction

The work (Ryabinin, 2007) describes the logical-probabilistic method (LPM), similar to the fault tree analysis (FTA) method described in (Vesely et al., 1981, 2002; Xing & Amari, 2008), but including four procedures: construction an event tree (risk scenario), construction a logical risk function, construction a probability risk function, calculation probabilities of derivative and final events.

The LPM method has become widely used for risk and safety management in technical systems (Ryabinin, 1991; Ryabinin & Cherkesov, 1981), the idea was developed in works (Henley & Kumamoto, 1992).

However, FTA and LPM methods have not been previously applied for risk and safety management in socio-economic systems.

To the end of XX century, risk management technologies in socio-economic systems have achieved a new stage of evolution due to the new methods for quantitative risk assessment. New tasks have arisen for assessment and analysis of reliability of economic systems (companies, banks, borrowers, government bodies). Risk in business is a common and widespread phenomenon; therefore, often there is sufficient statistics of homogeneous cases to assess probabilities of initiating events. The use FTA or LPM in economics is promising great opportunities for risk management.

The LPM method for risk management in socio-economic systems was applied for the first time by Solozhentsev (2017) (safety management of socio-economic systems), Alexeev V.A. (logical and probabilistic risk management for security portfolio, synthesis and analysis of probabilities) (Karaseva & Alexeev, 2015), Karasev (2015) (assessment and management of credit risk in a bank), Karaseva (2016) (operational risk management in the bank).

Risk management in socio-economic systems has features which cause requirements to modify the LPM method for assessment and analysis of risk in socio-economic systems. In order to better understand the specifics of the problem, let present a brief analysis of the common features and differences between technical and socio-economic systems.

Problem Statement

The concept of "system" is widely used and plays a great role in various sciences: chemistry, physics, biology, etc. From the viewpoint of system analysis (Wasson, 2016), in socio-economic sciences this concept reflects such characteristics as connections, integrity, internal and external environment, functional role of elements.

In this article, we will understand the system as an integral set of elements and connections between them. Note, this definition does not reflect the diversity of systems. The elements can be different and the connections between them are various, and the nature of the integrity also differs in different systems.

A technical system (TS) is an integral set of a finite number of interconnected material objects, which has consistently interacting sensory and executive functional parts; a model of predetermined behaviour of objects in the space of equilibrium stable states; and the ability, when object is in, at least, one of states (target state), independently perform the consumer functions provided by system’s design in normal situation.

The socio-economic system (SES) is an integral set of interrelated and interacting social and economic institutions (agents) and relations regarding the production, distribution and consumption of material and non-material resources, exchange and consumption of goods and services.

General properties:

1. Completeness. A change in any component of the system affects its other components and leads to a change in the system as a whole. Such phenomenon can be traced, for example, in the SES, in the case of dialectical interaction of productive forces and production relations - if production relations and the whole system change then the means of production change. That is, in this case, there is an interdependence of the economic system components.

2. Hierarchy. This means that each system can be considered as an element of a higher order. For example, the economy of Russia, as a transitional one, can be considered as one of the elements of the world economy.

3. Integrity. The system as a whole has properties which are absent in system’s elements (for example, the labour division, which is possible only with a certain number of producers). The vice versa situation is also true, elements can have properties that are not valid in the system as a whole.

As we can see, TS and SES have a number significant features, the main difference is a more comprehensive definition of a SES in the ontological sense. TS can be part of a socio-economic system. Also, the human factor plays a large role. The last aspect is especially important for our research.

In modern practical literature, the concept of "socio-economic system" is often identified with the concept of "organization" (Daft, 2012). This is convenient for description and explanation all phenomena of the SES, because the organization in a generalized representation determines all parameters and features: the human factor, integrity, connections, structure, etc.

The concept of "organization" is considered as a relatively isolated structural unit in the general system of social labour division. The criteria for such isolation are economic independence, organizational integrity, management system, aims and the overall result of joint activities of people.

Organization can be considered as a separate firm, enterprise, office, joint-stock company, bank, company (for example, insurance, tourism, etc.), as well as structural divisions of the public administration bodies.

Research Questions

For complex TS, the structural model (event tree) is constructed as a functional integrity scenario (Ryabinin, 2007), which includes system elements and connections between them (the structure and topology of the system are taken into account), or according to the dangerous state scenario (Solozhentsev, 2013). If the event Zi, i = 1, ..., n corresponds to working state of the i-th element of the system, and event Y is the working state of the system, then the logical connections between events can be interpreted as analogs of serial and parallel connection in electrical engineering.

For complex SESs, event trees are constructed under the structure of the initial data, for example, credits in research (Karasev, 2015); under the organizational structure of the company (Solojentsev & Karasev, 2010), under the diagram of business processes - as a further development of the EPC notation (Karaseva, 2018) (EPC notation is described in (Aalst van der, 1999); or under the scenario of the a dangerous state evolution (Solozhentsev, 2013). As we can see, in socio-economic systems, the ways of constructing event trees are more diverse.

Based on the systemic properties of SESs described above, we make conclusion, events in SESs can have different nature, and can be not only “failure” type. The work (Solozhentsev & Karasev, 2020) describes various types of models corresponding to different event trees, and also makes an attempt to classify initiating events in SESs. Seven types of events have been introduced.

Although there are large number of successfully solved problems in TSs (Dugan et al., 1993) and several ones in SESs (Solozhentsev, 2017), FTA and LPM methods have critical disadvantages:

1. Methods can be applied only if events are independent. Technological failures are often caused by independent events, but in economics, many initiating events are dependent.

2. Methods do not take into account the time factor in the logical connection "AND". Calculation with use of probabilistic function (multiplication of probabilities) gives us the probability of the simultaneous realization of events, which, in real life, practically does not happen. As a rule, events occur one after the other at different times, in any sequence, and the probability of the final event cannot be equal to the probability of their simultaneous realization (the so-called "conjunction error").

3. The problem how to obtain the probabilities of initiating events. Estimation of probabilities of initiating events is a nontrivial task in the absence of sufficient statistical data. Expert assessments are subjective and imprecise (Nichols, 2017). The probabilities are constantly changing over time. The model should be retrained periodically (Karasev, 2015).

4. Subjectivity when a tree of events (structural risk model) is constructed. Event trees, constructed under scenarios of a system’s dangerous state evolution, reflect the subjective opinion of the developer, his personal mind about the nature of the disaster and the set of initiating events. Each expert in his own way defines the set of events leading to the final event.

We need to develop the modification for LPM to overcome the difficulties be applied in risk management in in socio-economic systems.

Purpose of the Study

The above-mentioned problems have already arisen in the task of assessment and analysis the risk of the successful realization St. Petersburg Development Strategy until 2030. In the work (Karasev, 2016), a tree of events, logical and probabilistic models for the realization of the Strategy were constructed, the probability of successful realization of the Strategy was calculated and this probability is too low. The reason is in the large number of random initiating events (realization of individual development programs) connected by a logical connection "AND". As a result, the probability of a final event (realization of the Strategy) was calculated as the probability of the simultaneous realization of all initiating events. In fact, the Strategy is considered as successfully realized when all the initiating events realize (all development programs will be successfully completed), but the problem is that the programs are being realized during several years and are not completed at one time moment. All initiating events realize at different times, but a derivative event realizes when all initiating events will be realized.

There are difficulties in the practical application of FTA and LPM. Difficulties are associated with the multivariate construction of scenarios, the dependence of events and various sequence of their realization. In (Yellman et al., 1975), a method for calculations in case the sequence of events is proposed. This is a method of exhaustive search for the set of initiating events and their possible combinations. This method is technically difficult to implement for a complex system.

Research Methods

Now, let look the problem of event dependency. Let assume some initiating events are dependent. Then every event will have several probabilities of realization: one of them is the probability of the realization regardless of other events, the others are the probabilities of the realization of the considered event, depending on the realization of other events. We denote the set PA_i as the non-empty set of probabilities of the event Z_i, PA_i = {P(Z_iZ₁), P(Z_iZ₂), P(Z_iZ₃), …, P(Z_i), …, P(Z_iZ_n-1), P(Z_iZ_n)}, i = 1, ... , n.. If we order the elements of this set (probabilities) in ascending, then we get an ordered set PА_i (cortege), each element P(Z_i) from PА_i is located inside the closed interval [P(Z_iZ_j)_min; P(Z_iZ_j)_max], where P(Z_iZ_j)_min and P(Z_iZ_j)_max are respectively the minimum and maximum probabilities of realization Z_i, i = 1,…, n, j = 1,…, n from the set PA_i.

To solve the problem of event dependence, we propose use interval estimations of probabilities instead of point estimations. If we have the probability of initiating event as interval, the boundary values are in the range [0; 1], then we can take into account the influence other events on this probability, at least, those of them which are associated with this event by correlations. Also, the problem of time factor in the sequence of events ("conjunction error") is being solved.

Each initiating event Z_i, i = 1, …, n is assigned an interval probability P(Z_i) = [P(Z_{i min}); P(Z_{i maх})], i = 1, …, n. The calculation of the interval probability P (Z_i) of the derivative event Z_i is performed according to the rules of addition and multiplication of probabilities (Ventsel, 1969) and interval mathematics (Alefeld & Herzberger, 1983). The semantics of the formula for the calculation is determined by the rules of addition and multiplication of probabilities, and the arithmetic operations are performed according to the rules of interval mathematics.

Here are the rules for arithmetic operations with intervals of real numbers:

Addition: [a, b] + [c, d] = [a + c, b + d]

Subtraction: [a, b] - [c, d] = [a - d, b - c]

Multiplication: [a, b] [c, d] = [ min(ac, ad, bc, bd), max(ac, ad, bc, bd) ]

Division: [a, b] / [c, d] = [ min(a/c, a/d, b/c, b/d), max(a/c, a/d, b/c, b/d) ]

The distributive property is valid place in a weakened form: X(Y+Z) XY + XZ.

Addition and multiplication of intervals are commutative and associative.

Now let demonstrate operations with interval estimations of probabilities using several numerical examples.

Findings

Construction an event tree, according to the scenario of the dangerous system’s state evolution, depends on the experience and knowledge of expert or risk manager and contains large share of subjectivity. Experts sometimes neglect certain events that can lead to disaster. This phenomenon is explained by the qualifications of the experts, the impossibility of a complete enumeration of the space of events and problem in the assessment of probabilities due to the incompleteness of the initial information. As a rule, event trees in socio-economic systems are scenarios that reflect the opinions of people.

In SESs, like in TSs, there is no clear criterion for the correctness of the scenario, many details depend on the subjective opinion of the expert who constructs the scenario. Different experts will construct different scenarios and include different events in the tree. Nevertheless, there is a certain set of events that most experts will definitely include in the model, for example, events associated with changes in macroeconomic indicators, market indexes, events of a political situation or natural phenomenon, etc.

For the practical application of scenario event-driven management of risk and safety in SESs (Solozhentsev, 2017), we need to solve a complex problem, namely, to identify significant initiating events from the entire set of events and their probabilities.

Such events form a closed subsetof the finite space of possible random events , see Figure 1, the so-called Borel’s subset (Debs & Raymond, 2009). The Borel sigma-algebra (-algebra) of random events contains many “simple” sets: all intervals, half-intervals, segments and their countable combinations.

See Full Size >

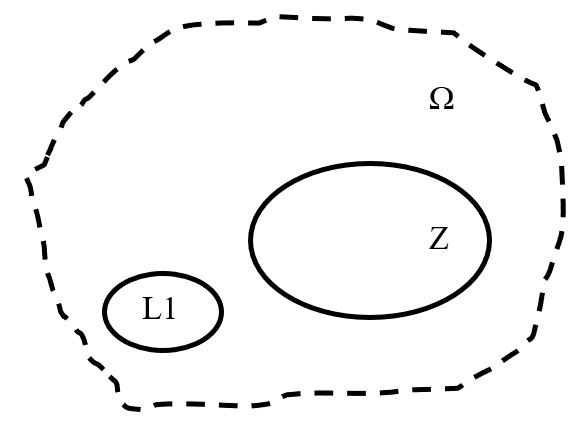
Set Z, whose elements are subsets of the set (not necessarily all), is called an -algebra if the following conditions are satisfied:

• Ω Z, - (-algebra of events contains a reliable event);
• If A Z, then A-  Z - together with any event, the -algebra contains the opposite event;
• If A1, A2, …, An Z, то A1 A2 … An Z - together with any countable set of events, the -algebra contains their union.

Random events that are not included in the event tree (scenario) form the space of latent events L, i.e., the following relations hold:

L = / Z, = L Z.

These events are not taken into account in scenarios; they play the role of unconsidered events (hidden, implicit factors, processes, phenomena). Therefore, they are not included in the model - event trees. Their probabilities are unknown and their nature is also unknown.

In theory, we can introduce a number of fictitious events into the model (set L1 in Figure 1) to take into account the latent events of the set L and calculate the risk by interval probabilities of their realization, using, for example, the intuitive Fermi method, described in (Poundstone, 2012). To do this, we use all available information about other random events of the set , the current parameters of the system and the parameters of the environment.

If we consider the topology of the risk structural model (event tree, scenario of a dangerous state evolution) in SESs, then, in general, we will see the graph G: = (Z, A), where Z is the set of vertices of the graph G, A is the set of arcs of graph G. Vertices Z₁, Z₂, …, Z_n-1 are events, and the graph is a event tree. Each of the events Z₁, Z₂, …, Z_n-1 can be either a separate initiating event or a subgraph.

If the set of fictitious events L1 = {Z_{1 L1}, Z_{1 L1}, …, Z_{k L1}}, corresponding to latent events, is included in the graph, we obtain the graph G: = (V, A), where V: = Z L1, L1 L, Z L1: = 0.

This approach complicates the event tree and does not solve the problem of estimation the probabilities of rare events or events that are absent in statistics.

The solution of the problem is the use of interval probabilities. According to Kolmogorov's axiomatics (Kolmogorov, 1956), the probabilistic space is given by the set , -algebra and a function P defined on , which assigns to each event B the value P(B), which is the probability B.

In our case, for the set of events Z= {Z₁, Z₂, …, Z_n} we have a function P(Z) with the domain dom(P(Z)), and for the set L= {L₁, L₂, …, L_k} accordingly, we have a function P(L) with domain dom(P(L)).

The space is finite, the transition from point values of the function P(Z) to interval values leads to extension dom(P(Z)) and a simultaneous narrowing dom(P (L)).

Since the functions are defined on a finite space, in some cases dom(P(Z)) covers the dom(P(L)), which leads to an implicit consideration of probabilities of latent events in the probabilistic functions (2) and (4).

Determining new events from and their probabilities, we also change the structure of the probabilistic space of random events . Determining the Borel subsets of events, we change the multidimensional state space of the system.

Conclusion

The problem of accurate estimation of probabilities due to the poor statistics of homogeneous events and their outcomes was noted in (Karasev, 2019). In the same work, the author proposes to use interval probabilities instead of point ones and a numerical example is given.

For some frequent events (assessment of credit risk in a bank, forecasting stock returns), we can collect statistics of homogeneous cases, which is applied to estimate probability using the frequency of events as a first probability approximation (Karasev, 2015). Probability estimations are used as arguments of a probabilistic function in a LPM approach, described in (Ryabinin, 2007).

Accurate point estimations of the probabilities of events in the set can be obtained using statistical data (Karasev, 2015) or expert estimations by the method of randomized summary indexes (Karaseva & Alexeev, 2015). In most cases, there is impossible to obtain accurate point probabilities, but we can estimate the upper and lower limits of these probabilities. Similar way was offered in (Karaseva, 2016) to calculate capital reservation volume for operational risk in banks as interval value.

Therefore, to simplify calculations, it is more effective to calculate the interval value of the probabilities), based on the values)). Moreover, the Fermi method and the method of randomized summary indexes are convenient to obtain expert interval estimations.

The use of interval probabilities allows overcome several disadvantages of methods FTA and LPM, namely:

• taking into account the time factor in the logical connection "AND";
• the ability to calculate probability of a final event in the case of dependent initiating random events;
• subjectivity of experts in construction event trees (risk scenario).

The last disadvantage is partially eliminated due to the implicit consideration of the influence of latent events in the interval estimation of the probability. The probabilistic space for events Z corresponds to set of probabilities P. The set of interval estimations expands the set P, transforming P from a strict set to a fuzzy one; the expansion P leads to cover partially the probabilistic set of latent events L1. Extension leads to a change in the structure of the probabilistic space of random events , this follows from the postulates of the Borel -algebra of events.

The article contains examples of calculations for logical connections "AND", "OR" for cases of dependent and independent initiating events, their probabilities is represented by both a point value and an interval one. The possibility of calculation interval probabilities of final events is shown.

The proposed adaptation of the FTA and LPM methods does not reject the traditional approach using point estimations of probabilities. If it is possible to estimate the probability accurately, then point estimations should be used, in other cases - interval estimations. Author suggests always use interval estimations in case of event dependencies and logical connections "AND" to obtain adequate values ​​of the probabilities for derivative and final events.

After obtaining an interval estimation of the probability, a transition to a point estimation is always possible. The way of such transition is described in (Uzhga-Rebrov & Kuleshova, 2020).

The interval estimations of probabilities also simplifies to obtain probabilities of initiating events by experts, for example, by the method of summary randomized indexes (Karaseva & Alexeev, 2015).

Of course, interval estimations of probabilities lead to a decrease in accuracy, but we note, most of the initial data for probabilistic models are obtained by expert way (due to insufficient volume of statistical data), which leads to a significant decrease in the accuracy and subjectivity of estimations.

References

• Aalst van der, W. M. P. (1999). Formalization and Verification of Event-driven Process Chains. Information & Software Technology, 41(10), 639-650.

• Alefeld, G., & Herzberger, J. (1983). Introduction to Interval Computations. Academic Press, Publishers New York, London, Paris, San Diego, San Francisco, San Paolo, Sydney, Tokyo, Toronto.

• Daft, R. L. (2012). Organization Theory and Design, 11. Cengage Learning, Mason, USA.

• Debs, G., & Raymond, J. S. (2009). Effective Refining of Borel Coverings. Trans. Amer. Math. Soc., 361, 2831-2869.

• Dugan, J. B., Bavuso, S. J., & Boyd, M. A. (1993). Fault Trees and Markov Models for Reliability Analysis of Fault Tolerant Systems. Reliability Engineering and System Safety, 39, 291-307.

• Henley, E. J., & Kumamoto, H. (1992). Probabilistic Risk Assessment. IEEE Press.

• Karasev, V. V. (2015). Monitoring and Crediting Process Control with Use of Logical and Probabilistic Risk Model. International Journal of Risk Assessment and Management, 18(3/4), 222-236.

• Karasev, V. V. (2016). Risk Management In Megalopolis Development Strategy. Regional Informatics and Informational Safety Conference, Proceedings, Issue 2, 173-177.

• Karasev, V. V. (2019). Problem of Logical And Probabilistic Method Adaptation For Aims of Management in Socio-Economic Systems. Modeling and Analysis of Safety and Risk in Complex Systems. Proceedings of the Fifteenth International Scientific Conference MASR - 2019 (Saint-Petersburg, Russia, June 19 – 21, 2019), 106 -110. (in Russian).

• Karaseva, E. (2016). Ability of Logical and Probabilistic Model for Operational Risk Management. Reliability. Theory & Applications, 11 3(42), 23-32.

• Karaseva, E. I. (2018). Bases of Process-Event Approach to Estimation of Operational Risk in Commercial Bank. Scientific Vestnik: Finances, Banks, Investmentss 4(45), 105-113.

• Karaseva, E. I., & Alexeev, V. V. (2015). Synthesis and Analysis of Probabilities of Events by Non-Numeric, Inaccurate and Incomplete Expert Information. International Journal of Risk Assessment and Management, 18(3\4), 222 - 236.

• Kolmogorov, A. N. (1956). Foundations of the Theory of Probability. Chelsea Publishing Company.

• Nichols, T. M. (2017). The Death of Expertise: The Campaign Against Established Knowledge and why it Matters. Oxford University Press, USA, New York.

• Poundstone, W. (2012). Are You Smart Enough to Work at Google? Back Bay Books.

• Ryabinin, I. A. (1991). Concept of Logical and Probabilistic Theory of Technical System Security. Shipbuilding industry, 21, 15-22.

• Ryabinin, I. A. (2007). Reliability and Safety of Structural Complex Systems. SpbSU.

• Ryabinin, I. A., & Cherkesov, G. N. (1981). Logical and Probabilistic Methods of Structural Complex System Reliability Research]. Radio and Communication, 264.

• Solozhentsev, E. D. (2013). Risk Management Technologies (with Logic and Probabilistic Models). Springer.

• Solozhentsev, E. D. (2017). The Management of Socioeconomic Safety. Cambridge Scholars Publishing.

• Solojentsev, E. D., & Karasev, V. V. (2010). I3-Technology for Counteraction to Bribes and Corruption. Problems of risk analyses, 7(2), 54-65.

• Solozhentsev, E., & Karasev, V. (2020). The Digital Management of Structural Complex Systems in Economics. International Journal of Risk Assessment and Management, 23(1), 54-79.

• Uzhga-Rebrov, O., & Kuleshova, G. (2020). Conditioning Interval Probabilities. Modeling and Analysis of Safety and Risk in Complex Systems: Proceedings of the Sixteenth International Scientific Conference MASR - 2020 (Saint-Petersburg, Russia, June 23 – 25, 2020), Edited by E. Solozhentsev, V. Karasev, 63-69. (in Russian).

• Ventsel, E. S. (1969). Probability Theory. Science.

• Vesely, W. E., Goldberg, F. F., Roberts, N. H., & Haasl, D. F. (1981). Fault Tree Handbook. U.S. Nuclear Regulatory Commission, NUREG–0492.

• Vesely, W., Dugan, J., Fragola, J., Minarick, J., & Railsback, J. (2002). Fault Tree Handbook with Aerospace Applications. NASA Office of Safety and Mission Assurance, Washington DC.

• Wasson, C. S. (2016). System Engineering Analysis, Design, And Development. Concepts, Principles, and Practices. John Wiley & Sons Inc., Hoboken, New Jersey.

• Xing, L., & Amari, S. V. (2008). Fault Tree Analysis. In Handbook of Performability Engineering. Springer.

• Yellman, T. W., Powers, G. J., Fussell, J. B., & Kuwamoto, H. S. (1975). Comments on “Fault Trees – A State of the Art Discussion”. IEEE Trans. Reliability, R-24, 344-347.