Formalization Of The Impact Of Costs On The Reliability Of Instrument-Making Products

Abstract

The influence of cost costs on the reliability of products is not in doubt, but the ideas about this influence are more intuitive than scientifically based. Therefore, a formalized assessment of the impact of cost costs on the reliability of radio-electronic equipment is of some interest, which was the subject of scientific research in this article. When evaluating the increase in the cost of production due to raising reliability requirements, it is necessary to choose a certain initial level, relative to which the assessment is made. The ratio of this level of reliability to the designed one can be used as a measure to increase the reliability of the newly developed radio-electronic equipment. In this paper, we derive formulas that demonstrate an analytical link of the cost and reliability of radio-electronic equipment and, under certain conditions, they can be implied to set up the optimal values of the indicators of the probability of failure-free operation and the average time to failure.

Keywords: Costs, optimization, radio-electronic equipment, reliability

Introduction

In 2005, Japan developed and implemented the JIS/TR Q 0005:2005 standard "Quality management systems. Guide to sustainable development", the conceptual provisions of which are incorporated in the new edition of ISO 9004 (Emmanouil, 2020; Gumus, 2018).

In accordance with the new concept is developed in a new direction in the solution of quality problems is the development of sustainable success in today's competitive consumer market due to the implementation of improvements and innovations, and management of risks, opportunities and knowledge of the environment on the market. (Kima et al., 2019; Vershinin, 2018).

At the same time, innovation is understood as the result of creative activity aimed at the development, creation and distribution of new products, technologies, inventions, and management methods. (Lu & Zhou, 2019; Tang et al., 2020).

Problem Statement

Creative work on the development of complex instrument-making products is usually carried out of the constants the conditions of multi-criteria, uncertainty of practical situations and significant cost costs. (Davydova & Reutov, 2018; Meguetta et al., 2015).

For restored instrument-making products and, in particular, multiple-use radio-electronic equipment (REE), the value of operation is determined by the cost of maintenance, repair, power supply and damage that may be caused by the risk of its unreliable operation.

Research Questions

Reliability is one of the properties of the quality of any industrial product. For complex REE products, obtaining the necessary level of reliability requires significant material and labor costs, which determines the economic characteristics of REE. (Bowen et al., 2017; Haselgruber et al., 2021).

In general, the influence of cost costs on the reliability of products is not in doubt, but the ideas about this influence are more intuitive than scientifically based in the form of specific.

Purpose of the Study

Therefore, an analytical (formalized) assessment of the impact of cost costs on the reliability of REE is of some interest, which was the subject of scientific research in this article (Love et al., 2019; Samokhin et al., 2020).

Research Methods

The total cost of reliability-related costs can be represented as the sum of

$C=C_{\ni }+C_n$ (1)

where Cэ - is the cost of operating costs, depending on the reliability;

С_n - the cost of production costs, due to the cost of improving reliability in the development and manufacture of REE (Caia et al., 2020).

Assuming that the failure rate of the REE will be constant during operation, the expected number of repairs can be found by the formula

$P\left(t\right)=\exp \left\{-n\frac{t}{T_P}\right\};$ (2)

where - is the number of failures during the total operating time;

- total operating time of REE for a certain period (resource);

- the specified operating time of the REE.

From this formula we find

$n=-\frac{T_p}{t}\ln P\left(t\right).$ (3)

If the cost of one failure, then the cost of the failures

$C_{\ni }=C_{1}n$ (4)

Substituting in (4) the value from (3), we get

$C_{\ni }=-C_1\frac{T_p}{t}\ln P\left(t\right)$ (5)

When evaluating the increase in the cost of production due to raising reliability requirements, it is necessary to choose a certain initial level, relative to which the assessment is made. As Usually, the existing level of reliability up to day of the development of the REE is chosen, expressed by the average failure rate ${\lambda }_{CP}$ (Podolyakina, 2017; Woo, 2019).

The ratio of this level of reliability to the designed one can be used as a measure to increase the reliability of the newly developed REE (Shi et al., 2020).

The cost of production costs to improve reliability can be expressed as a dependency.

$C_{\mathrm{\Pi }}=C_0{\left(\frac{{\lambda }_{CP}}{{\lambda }_{CP.\mathrm{\Pi }}}\right)}^{\alpha }$; (6)

where - is the cost of additional costs to ensure the reliability of the REE, similar to the newly designed one;

${\lambda }_{CP.\mathrm{\Pi }}$- average failure rate of the designed REE;

$\alpha$ - a coefficient that depends on experimental data, a value close to one (approximately from 0.5 to 1.5).

From (6) it can be seen that an increase in reliability by a factor of 10 leads to additional costs:

$C_n=C_0{10}^{\alpha }$ (7)

At $\alpha =1$ the cost of costs $C_n=10C_0$, i.e. additional costs increase in proportion to the increase in reliability (decrease in the failure rate).

From (6), you can get

$C_n=C_0{\left(T_{cp}N{\lambda }_{cp}\right)}^{\alpha }$ (8)

where $T_{cp}$- time to failure;

- is the number of REE elements.

Given that $T_{cp}=-\frac{t}{\ln P\left(t\right)}$, we get:

$c_n=C_0{\left(Nt{\lambda }_{cp}\right)}^{\alpha }{\left(-\frac{1}{\ln P\left(t\right)}\right)}^{\alpha }$ (9)

Using (5) and (9), the total cost of reliability-related costs can be found by the formula

$C=C_1\frac{T_p}{t}\left[-\ln P\left(t\right)\right]+C_0{\left(Nt{\lambda }_{cp}\right)}^{\alpha }{\left(-\frac{1}{\ln P\left(t\right)}\right)}^{\alpha }$ (10)

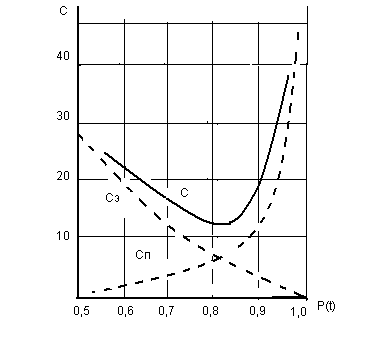
It can be seen from (10) that operating costs decrease with increasing REE reliability, and production costs increase.

Obviously, with a certain amount of reliability, the total costs will have a minimum. It is not difficult to find it from (10). To do this, take the derivative of the software $P\left(t\right)$ and equate it to zero (Pokorni, 2016; Raghavaiah & Prasad, 2019).

Introducing the notation $k_1=C_1\frac{T_p}{t}$, $k_2=C_0{\left(Nt{\lambda }_{cp}\right)}^{\alpha }$, making differentiation and equating the resulting expression to zero, we find:

${\left[-\ln P\left(t\right)\right]}^{\alpha +1}=\frac{k_2}{k_1}\alpha$ (11)

or

$\left[-\ln P\left(t\right)\right]=\sqrt[\alpha +1]{\frac{k_2}{k_1}\alpha }$. (12)

Given that $\left[-\ln P\left(t\right)\right]=\ln \frac{1}{P\left(t\right)}$, we find the optimal reliability

$P_{onm}\left(t\right)=\exp \left[-\sqrt[\alpha +1]{\frac{k_2}{k_1}\alpha }\right]$ (13)

After substituting the formulas for $k_1$ and $k_2$, we will have

$P_{O\mathrm{\Pi }T}\left(t\right)=\exp \left[-\sqrt[\alpha +1]{\frac{C_0{\left(Nt{\lambda }_{cp}\right)}^{\alpha }t\alpha }{C_1{T}_P}}\right]$ (14)

Here ${\lambda }_{cp}$ it is determined based on the experience of operating the REE. The value $\alpha$ is found as the ratio of the cost gain to the logarithm of the reliability gain:

$\alpha =\frac{\ln \frac{C_n}{C_0}}{\ln \frac{{\lambda }_{cp}}{{\lambda }_{cpn}}}$. (15)

When $\alpha =1$ (14) takes the form

$P_{o\mathrm{\Pi }T}=\exp \left[-\sqrt{\frac{C_{0}N{t}^2{\lambda }_{CP}}{C_1{T}_P}}\right]$ (16)

From where

$T_{CPonm}=-\frac{t}{\ln P_{o\mathrm{\Pi }T}\left(t\right)}\sqrt{\frac{C_1{T}_p}{C_{0}N{\lambda }_{CP}}}$ (17)

Findings

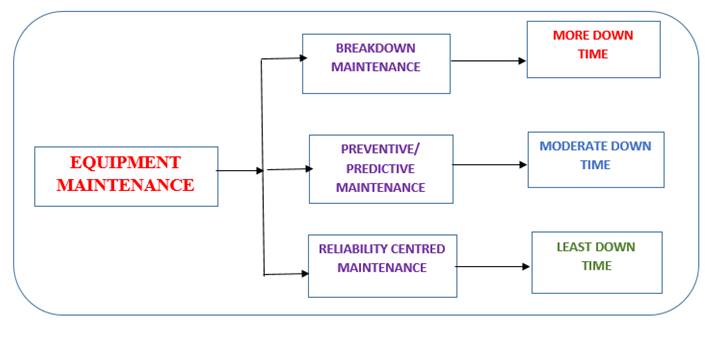
Equipment maintenance strategies with respect to down time shown in the Figure 1. It is inferred that reliability centred maintenance made improved availability of equipment over other maintenance types.

See Full Size >

The impact of the cost of operation and production on the total cost is illustrated in the graph below (at $\frac{T_P}{t}=\mathrm{}\mathrm{20}$) (see Figure 2).

See Full Size >

Conclusion

Thus, formulas (16) and (17) demonstrate an analytical link of the cost and reliability of REE and, under certain conditions, they can be implied to set up the optimal values of the indicators of the probability of failure-free operation and the average time to failure.

References

• Bowen, Z., Yang, M., Emi-Reynolds, B., & Yoshikawaa, H. (2017). Reliability analysis of Digital Instrumentation and Control software system. Progress in Nuclear Energy, 98(07), 85-93. DOI:

  Google Scholar

  Crossref

• Caia, Y., Wu, Y., Zhou, J., Liu, M., & Zhang, Q. (2020). Quantitative software reliability assessment methodology based on Bayesian belief networks and statistical testing for safety-critical software. Annals of Nuclear Energy, 145(09), 107593. DOI:

  Google Scholar

  Crossref

• Davydova, T. I., & Reutov, D. V. (2018). Comparative analysis of programs for calculating reliability: an automated system for calculating reliability and an automated system for ensuring the reliability and quality of equipment. Automation of control processes: sb.nauch. tr. Molodezh. sci. - tech. conf. Ulyanovsk. FNPC JSC «NPO "Mars", 1. 58-62.

• Emmanouil, K. (2020). Reliability in the era of electrification in aviation. A systems approach, Microelectronics Reliability, 113945, 114.

• Gumus, B. (2018). A reability approach from mechanical engineering point of view. Sigma J Eng & Nat Sci, 36(3), 629-644.

• Haselgruber, N., Capser, S. P., & Vignatic, G. I. (2021). Early life reliability growth testing with non-constant failure intensity. Procedia Computer Science, 180, 608-617. DOI:

  Google Scholar

  Crossref

• Kima, M., Seo, J., Jung, W., Choi, J. L., Kang, H. G., & Lee, S. G. (2019). Evaluation of effectiveness of fault-tolerant techniques in a digital instrumentation and control system with a fault injection experiment. Nuclear Engineering and Technology, 51(3), 692-701.

• Love, P., Zhou, J., & Matthews, J. (2019). Project controls for electrical, instrumentation and control systems.

• Lu, В., & Zhou, X. (2019). Quality and reliability oriented maintenance for multistage manufacturing systems subject to condition monitoring. Journal of Manufacturing Systems, 52(A), 76-85. DOI:

  Google Scholar

  Crossref

• Meguetta, Z., Conrard, B., & Bayar, М. (2015). Design of control system instrumentation using reliability criteria. IFAC-Papers On Line, 48(21), 1491-1496.

• Podolyakina, N. (2017). Estimation of the Relationship between the Products Reliability. Period of Their Warranty Service and the Value of the Enterprise Cost. Procedia Engineering, 178, 558-568.

• Pokorni, S. (2016). Reability predication of electronic equipment. Problem and experience, 595-600.

• Raghavaiah, N. V., & Prasad, I. H. (2019). Maintenance and reability strategy of mechanical equipment in industry. International Research Journal of Engineering and Technology (IRJET), 6, 3430-3432.

• Samokhin, D., Alslman, M., & Vostrilova, A. (2020). Verification the Reliability of Using (Non-Nuclear Grade). Electronic Devices in Nuclear Installations Procedia Computer Science, 169, 835-839. DOI:

  Google Scholar

  Crossref

• Shi, Y., Zhu, W., Xiang, Y., & Feng, Q. (2020). Condition-based maintenance optimization for multi-component systems subject to a system reliability requirement. Reliability Engineering & System Safety, 202(10), 107042.

• Tang, Y., Yuan, Y., & Liu, Y. (2020). Cost-aware reliability task scheduling of automotive cyber-physical systems. Microprocessors and Microsystems, 21, 103507.

• Vershinin, M. (2018). Suboptimal management model in technology of radio-electronic equipment. Issues of radio electronics, 10, 125-129.

• Woo, S. (2019). Reliability Design of Mechanical Systems. A Guide for Mechanical and Civil Engineers Second Edition, 476.