Digital Technologies In Mathematical Education

Abstract

The article discusses the issues of digitalization and integration of mathematics education. The use of information technologies in teaching mathematical disciplines on the basis of practice-oriented tasks has been substantiated. The integrative presentation of information is disclosed due to its compression, concentration, generalization, as an effective tool for rationalizing memorization and understanding. Integration of mathematical education obliges to consider objects and phenomena of reality in their interconnection and interdependence. In these conditions, the view on intra- and intersubjective connections changes. In a number of cases, mathematics should become not a source, but a consumer of the knowledge offered in the classroom in general professional disciplines, relying on ideas formed in the study of these disciplines. In the work, the issues of digitalization and integration of mathematical education are revealed on the basis of a practice-oriented problem in probability theory and mathematical statistics. An algorithm for studying the parameters of the binomial distribution using the MS Excel spreadsheet is presented. A study was carried out and it was shown that for a large number of trials n, the binomial distribution, even with p significantly different from 0.5, is fairly accurately approximated by the normal distribution. The use of information technologies in teaching mathematical disciplines contributes to an increase in the level of mathematical training of future specialists of the EMERCOM of Russia, as well as the formation and development of professional motivation.

Keywords: Digital technologies, mathematical education, digitalization of education

Introduction

The digitalization of mathematics education plays an important role in the formation of future fire safety engineers, techno sphere safety engineers, system analysis engineers of the crisis management center, forensic lawyers and other employees of the EMERCOM of Russia.

The relevance of mathematical education in the 21st century for specialists of the Ministry of Emergency Situations of Russia is due to forecasting hazardous factors of fire, conducting, monitoring the fire situation, predicting natural disasters, emergency situations (ES) of a man-made nature, emergencies of a natural nature, assessing the elimination of the consequences of natural disasters, preventing emergencies.

At the level of higher education in the universities of the Ministry of Emergency Situations of Russia, mathematical knowledge is used in the process of studying professional disciplines: Investigation and examination of fires, Fundamentals of scientific research, Fire safety of technological processes, Reliability of technical systems and technogenic risk, Metrology, standardization and certification, Theory of combustion and explosion, Safety life activity, Information systems theory, Systems modelling, Communication and warning systems, Engineering and space monitoring systems, Crisis management in emergency situations, Automatic control theory and others.

For the successful mastering of a block of mathematical disciplines in the system of training future specialists of the EMERCOM of Russia, a problem-oriented combination of knowledge from various branches of mathematics is necessary, which implies obtaining a resulting synergistic effect.

This effect can be achieved only if the resulting synergistic configuration is well suited to the practice-oriented problem being solved, which must be pre-structured, and information links for input and output will be established between private local subtasks.

For the formation of synergetic configurations and the establishment of information links between them, an additional mechanism is needed - a mechanism for integrating knowledge. Such a mechanism makes it possible to harmonize the elements of the mathematical apparatus aimed at improving the quality of assimilation of knowledge on the techniques and methods of solving practice-oriented problems in the system of training future specialists of the EMERCOM of Russia.

The integrative presentation of information, due to its compression, concentration, generalization, is an effective tool for rationalizing memorization and understanding. This level obliges to consider objects and phenomena of reality in their interconnection and interdependence. In these conditions, the view on intra- and intersubject connections changes radically. In a number of cases, mathematics should become not a source, but a consumer of knowledge offered in classes in general professional disciplines, relying on ideas formed in the study of these disciplines (Artamonov et al., 2017; Batkovskiy et al., 2015, 2017; Motorygin et al., 2016; Trofimets, 2020).

Integration is one of the promising innovative techniques that can solve many of the problems of modern subject-separated professional education. The concept of subject-centrism is not opposed to integration, and the development of the vocational education system does not follow the path of limiting or replacing one principle with another.

The learning process takes place within the boundaries of a separate subject precisely because it is an integrated system. Subject-centrism and integration are two dialectically interrelated positions that condition each other. In practice, subject-centrism is an external form of intra-subject integration. Modern trends in the development of the vocational education system imply the use of integration as one of the promising innovative techniques, but it is important to understand that this process can and should occur not from subject-based holistic education to integration, but from intra-subject integration to inter-subject integration. Such a transition presupposes not the replacement, but the addition of one provision to another.

One of the ways to implement the integration of mathematical knowledge is modular-block connections, which are carried out in order to eliminate gaps in the knowledge, skills and abilities of students, as well as to generalize and systematize the educational material. The mechanism for implementing this level is as follows: in the discipline "Mathematics" content lines are highlighted, a list of basic questions and the amount of material for each line is indicated, their development is investigated, the main interdisciplinary connections that require consideration in the classroom are highlighted, a methodology for their organization is developed (Batkovsky & Trofimets, 2015; Selemeneva, 2018; Trofimets, 2008, 2009a, 2009b, 2012; Trofimets & Trofimets, 2019, 2020).

In this article, the focus is shifted to the use of the MS Excel spreadsheet processor when studying the parameters of the binomial distribution.

Problem Statement

This topic is relevant and significant in the professional activities of an engineer-analyst of the system analysis of a control centre in crisis situations, as well as an engineer for fire safety, an engineer for techno sphere safety and other employees of the EMERCOM of Russia.

The key point in the study of the parameters of the binomial distribution is the Bernoulli scheme.

Research Questions

A discrete random variable that takes non-negative integer values with a probability determined by the Bernoulli formula is called binomially distributed:

$P_n\left(m\right)=P\left(X=m\right)=C_n^m{p}^m{q}^{n-m}$

The mathematical expectation and variance of the binomial distribution are as follows:

$M\left(x\right)=np; D\left(x\right)=np\left(1-p\right).$

Purpose of the Study

Let's move on to the formulation of a professionally oriented problem and an algorithm for solving it in MS Excel.

A professionally oriented task.

It has been suggested that 3% of the city's population is infected with COVID19. In testing carried out by a mobile laboratory, samples were taken at random from 1,000 residents. What is the probability that there will be at least 20 infected people in the tested group, provided the test is completely reliable? Solve the problem using normal and binomial distributions.

Research Methods

Investigation of the binomial distribution.

The problem under consideration is essentially equivalent to performing 1000 Bernoulli tests with a probability of success in one test of 0.03.

To approximate the binomial distribution by normal, we find its numerical characteristics (Figure 1):

$M\left(x\right)=np=1000\times 0.03=30;$ $D\left(x\right)=np\left(1-p\right)=1000\times 0.03\times 0.97=29.1;$ $\sigma =\sqrt{D\left(x\right)}=5.39.$

See Full Size >

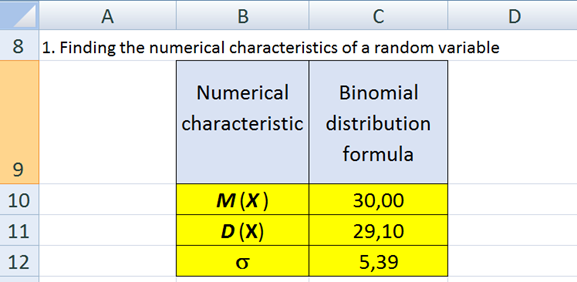
Since the normal distribution function is continuous, and the binomial distribution function is discrete, then to approximate the discrete interval between points 19 and 20 of the binomial distribution, we take the value 19.5 for the normal distribution.

For the normal distribution, since it is continuous, we have:

$P\left(x\ge 19.5\right)=P\left(x>19.5\right)=1-F\left(19.5\right).$

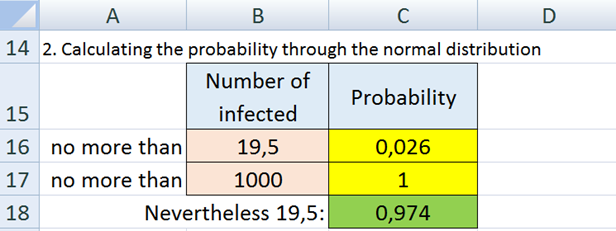
We use the found characteristics as arguments to the NORMDIST function: x = 19.5; Mean = 30; Standard_deviation = 5.39; Cumulative = 1.

x - Required. The value for which the distribution is plotted. In the problem under consideration, it is 19.5.

Average - Required. The arithmetic mean of the distribution. In the problem under consideration, it is 30.

Standard_deviation - Required. Standard deviation of the distribution. In the problem under consideration, it is 5.39.

Integral - Required. For the problem under consideration, takes the value 1 - TRUE.

A Boolean value that determines the shape of the function. If the argument is TRUE, NORMDIST returns the cumulative distribution function; if this argument is FALSE, the distribution weighting function is returned.

Figure 2 shows the calculation of the probability using the NORMDIST function.

See Full Size >

Findings

Let's calculate the required probability through the binomial distribution, while remembering that this distribution is discrete. Let's use the BINOMDIST function.

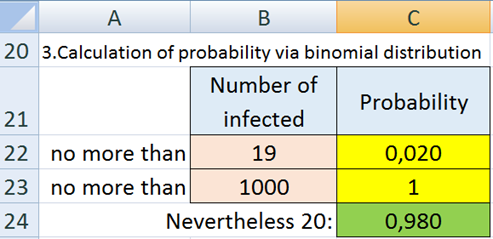
BINOMDIST function arguments: number_s = 19, trials = 1000, probability_s = 0.03, cumulative = 1).

Required. The number of successful tests for the problem under consideration is 19.

Trial Number - Required. The number of independent tests for the problem under consideration is 1000.

Probability_Success - Required. The probability of success of each test for the problem under consideration is 0.03.

Integral - Required. For the problem under consideration, takes the value 1 - TRUE.

A boolean value that determines the shape of the function.

If the argument is "integral" is TRUE, BINOMDIST returns the cumulative distribution function, ie, the probability that the number of successful test is not less than the value of the argument "Success_Number"; If this argument is FALSE, the function returns the probability measure, ie. e. the probability that the number of successful trials is equal to the value of the argument "Success_Number".

Figure 3 shows the calculation of the probability using the BINOMDIST function.

Comparing the values of the probabilities p calculated through the normal and binomial distributions, we arrive at the following result: = 0.974 using the NORMDIST function and= 0.980 using the BINOMDIST function.

For a large number of trials n, the binomial distribution, even for significantly different from 0.5, is fairly accurately approximated by the normal distribution.

See Full Size >

Conclusion

The use of information technologies in teaching mathematical disciplines contributes to an increase in the level of mathematical training of future specialists of the EMERCOM of Russia during the development of digitalization of education, as well as the formation and development of professional motivation.

In turn, the integration of mathematical knowledge orients the teacher to:

• presentation of the elements of the mathematical apparatus in unity and integrity;
• development and implementation of integrative lessons in mathematics for students in the context of digitalization of education.

The integration of mathematical knowledge of intra- and intersubjective connections allows you to systematize and implement a meaningful disclosure of the set of elements of the mathematical apparatus used in the educational process (Selemeneva, 2018; Trofimets, 2009b, 2012; Trofimets & Trofimets, 2019, 2020).

At the same time, the tendency to expand mathematical concepts is actualized: each subsequent concept includes in its content the meaning of the previous concept and adds more new components.

The use of modern information technologies in teaching mathematics to cadets of technical universities makes it possible to implement the phased formation of competencies formulated in the main professional educational programs.

Starting with basic examples of using computer systems in the classroom in mathematical disciplines, the teacher lays the foundation for the cadets of the integrative aspect of the use of mathematics, computer science and the disciplines of the professional cycle, develops practical skills in the cadets in the process of modelling practice-oriented problems.

References

• Artamonov, V. S., Ivanov, A. Y., Sharapov, S. V., Trofimets, E. N., & Trofimets, V. Ya. (2017). Information systems and processes in the analytical training of management scholars. Espacios, 38(25), 18.

• Batkovskiy, A. M., Semenova, E. G., Trofimets, E. N., Trofimets, V. Y., & Fomina, A. V. (2017). Statistical simulation of the break-even point in the margin analysis of the company. Journal of Applied Economic Sciences. Romania: European Research Center of Managerial Studies in Business Administration, XII, 2(48), 558-570.

• Batkovskiy, A. M., Semenova, E. G., Trofimets, V. Ya., Trofimets, E. N. & Fomina, A. V. (2015). Automated Rating of Financial and Economic Condition of Companies. Mediterranean Journal of Social Sciences. MCSER Publishing, Rome-Italy, 6(5-S4), 297-308.

• Batkovsky, A. M., & Trofimets, V. Ya. (2015). Decision Support Systems with Modules of Applied Mathematical Models and Methods. Problems of Radioelectronics, 9. 253-275.

• Motorygin, Y. D., Artamonov, V. S., Maximov, A. V., Trofimets, V. Ya., & Trofimets, E. N. (2016). Management of the Formation of Rating Preferences of Economic Entities upon Collective Choice. International Journal of Economics and Financial Issues, 6(4), 1956-1964.

• Selemeneva, T. A. (2018). Application of information technologies in the stage-by-stage formation of competencies in the university. Development of education, 1(1), 60-62.

• Trofimets, E. N., & Trofimets, V. Ya. (2019). Didactic aspects of the application of computer modeling technology in the educational process of students-economists. Institutional foundations of the economy of advanced development. Materials of the international scientific and practical conference. ed. L. G. Batrakova. (2019), (pp. 277-282). Publishing house: Yaroslavl State Pedagogical University. K. D. Ushinsky).

• Trofimets, E. N., & Trofimets, V. Ya. (2020). Research of numerical methods for solving ordinary differential equations in MS Excel. Journal of Physics: Conference Series (JPCS) Ser., 1691, 012049.

• Trofimets, E. N. (2008). Computer modeling in the educational process of economics students. Informatics and Education, 7, 118-119.

• Trofimets, E. N. (2009a). Conceptual model of the scientific and methodological apparatus for solving professionally oriented economic problems. Bulletin of the Peoples' Friendship University of Russia. Series "Informatization of Education", 20094, 107-117.

• Trofimets, E. N. (2009b). Integral approach in teaching mathematics to students-economists: monograph. Federal Agency for Education, State. educational institution higher. prof. education "Yaroslavl state. Technical University – Yaroslavl.

• Trofimets, E. N. (2012). Substantiation of an integrative approach to teaching mathematics to management students based on a map of the perception of an academic discipline. Alma mater (Vestnik vysshei shkoly), 6, 97-99.

• Trofimets, E. N. (2020). Investigation of the geometric meaning of the derivative using mathematical packages. Journal of Physics: Conference Series (JPCS) Ser., 1691, 012039.