Algorithm For Planning Efficient And Sustainable Crop Production

Abstract

The paper deals with the problem of optimal planning of the annual program of crop production at an agricultural enterprise. The dependences of crop yields on mineral nutrition elements are determined in the form of nonlinear dependences based on historical data series containing data on crop yields, reserves of mineral nutrition elements in the soil, doses of applied mineral and organic fertilizers. These dependencies are used to develop a fertilizer application plan and justify economically feasible levels of yields in the planning period. The placement of crops according to the best predecessors is formalized on the basis of expertly assigned information on the influence of predecessors in the crop rotation. To obtain cost-effective and sustainable solutions, an algorithm has been developed and tested that implements a series of statistical tests. Randomly selected characteristics of the external environment (parameters in analytical expressions of yields, sales prices, production costs) were compared with the extreme values of the marginal income corresponding to these conditions. Based on the results of statistical tests, the user was provided with information sufficient for a reasonable choice of an option that combines a high economic and financial result with a low risk of not receiving it.

Keywords: Agri-food system, crop rotation, mathematical model, optimization, planning

Introduction

The state of modern scientific knowledge about agri-food systems has both fairly wide modeling capabilities and certain limitations of such models. In this article, we will consider the possibilities of improving the management models of an agricultural enterprise, including making economic decisions and planning activities. Although modern mathematical models have the functionality that is necessary to solve various options for management problems, in practice they are rarely used and have great potential for improving them.

Current demands for the development of existing models range from how to manage enterprises more efficiently, what changes are needed to increase profitability without harming the environment, how to design a development strategy to adapt to the constant changes faced by agriculture, including climate change, changes in demand for agricultural products, price volatility, etc. Models should provide reliable solutions that should ensure the sustainability of the development of an economic entity.

The complexity of modeling an agricultural enterprise is due not only to the variability of external conditions, but also to the configuration of the internal parameters of the enterprise: its sectoral structure, qualifications and number of employees, material and technical base, especially farmland and the composition of farm animals, investment opportunities. Based on this, a whole set of possible combinations of variables that represent the parameters and conditions listed above looms before the developers. Taking into account all these circumstances and conditions, it is necessary to develop the best options:

• operational management of the functioning of an agricultural enterprise;
• an annual economic and financial plan;
• long-term development program of the enterprise for the future.

Various options for solving these problems by methods of mathematical modeling have regularly appeared in scientific publications since the 60s of the last century (Bellman & Dreyfus, 1965; Braslavets & Kravchenko, 1978; Csaki, 1988; Glen, 1987; Ognivtsev et al., 1997). They always noted that in multi-stage optimization systems, the role of correct information exchange is very important. The operational economic management of the production and marketing of agricultural products should use the indicators of the annual plan (possibly updated in the rolling planning mode) as benchmarks, and the enterprise development program should solve the problems of expanded reproduction with the provision of the necessary resources and technologies, as well as with taking into account forecasts of changes in exogenous variables.

The complexity of planning business processes increases many times as the considered organizational and economic relations between the production units of an agricultural enterprise and from an increase in the planning horizon. But it is precisely when planning such complex systems for the long term that the use of accurate quantitative methods provides the highest effect. The target optimal plan for the year of an agricultural enterprise should contain a solution to the main economic problems:

• specialization of production and its volumes;
• selection of technologies and their provision with all kinds of resources;
• planned distribution of manufactured products by sales channels.

The choice of the optimality criterion is of great importance in the formulation of the problem of optimal annual planning. The most commonly used de statements are: maximum profit with available resources and minimum cost for a given volume of production. The functioning of the system of optimal annual planning can be based on a well-known economic and mathematical model for optimizing the production and sectoral structure of an agricultural enterprise. To develop a mathematical model, the following data are required:

• the size of all types of resources (land, labor, capital) at the disposal of the economy;
• forecasts of the yields of all crops grown and the productivities of all types of livestock;
• prices for products and resources;
• standards and elasticities of replacement.

Calculations of the annual plan of the enterprise in the presence of a software implementation of the model can be made by the specialists of the enterprise itself, and remotely, as an Internet technology or a service of third-party firms or government services. The choice is currently small due to the minimum supply and is highly dependent on the implementation of the digitalization program at the district level.

It is necessary to dwell on the important aspect that the presence of predictive values of parameters in the model requires multivariate model calculations for various combinations of predicted variables. Naturally, enterprise managers have different degrees of risk appetite, and in this case, the multivariate calculations will allow choosing a solution in the interval "guaranteed result - maximum possible result".

The procedure for calculating the annual plan can be repeated throughout the year as necessary:

• in case of preparation of a serious decision that will affect the parameters of the plan;
• in case of a significant change in forecasts;
• at the end of the year to recalculate elasticities and normative data.

The plan optimization problem is solved by linear programming methods, an important advantage of which is the analysis of dual estimates. This allows us to identify the presence of active restrictions for further development, to assess the significance of each of them and, thus, to indicate promising directions for the development of the enterprise.

The transition of the enterprise to new directions of development, including new types of activity, involves the implementation of certain investment projects. Based on this, a long-term program for the development of an agricultural enterprise can be simplified as an agreed set of investment projects that must be provided with sources of financing, working capital, labor, and other resources (Romanenko, 2007; Romanenkov et al., 2004). With this approach, a direct analysis of the network schedule of projects is necessary, since their combination over time should take into account the possibilities of using revenues from completed projects and the optimal distribution of costs.

Problem Statement

Producers of crop products operate in a stochastic environment formed by the dynamics of weather factors, the state of the markets for consumable resources and agricultural raw materials. In these conditions, significant risks of losses arise for a commodity producer, and solving the problem of planning an economically efficient and sustainable production of crop products becomes especially relevant. The idea of ​​assessing the results of the interaction of the economic system with the external environment using simulation methods is not new and is often implemented in the form of stochastic linear programming problems. To a lesser extent, direct methods of statistical testing are used, which generate combinations "the state of the external environment is the result of an economically optimal production plan for this state." Subsequent statistical processing of the simulation results makes it possible to compare economic benefits with the associated risks and choose a combination that satisfies the manufacturer. This work illustrates the possibilities of the method using the example of a manufacturer of crop products.

Research Questions

Within the framework of the article, the authors have solved the following tasks:

• to illustrate the method, an economic and mathematical model of crop production has been developed, the parameters of which have interval limitations;
• developed an algorithm for simulation modeling, which implements random combinations of states of the external environment;
• researched a lot of planned decisions of the manufacturer to optimize the distribution of acreage for cultivated crops in connection with variations in the external environment;
• many combinations of the economic result with its coefficients of variation have been obtained, which allow the manufacturer to choose an effective and sustainable solution.

Purpose of the Study

The purpose of the study is to develop and substantiate the productivity of methods for obtaining cost-effective and sustainable solutions when planning crop production in a stochastic external environment.

Research Methods

Formation of a production plan that maximizes future profits with acceptable risks is a basic task that every crop production manufacturer solves annually. The economic and financial result of the enterprise, the possibility of reproduction of capital and further development directly depend on the success of its solution.

We will distinguish between two types of such problems. By the decision in the narrow sense we mean the development of an annual plan for adjusting the sectoral structure of crop production, in combination with the rational distribution of resources over the cultivated areas occupied by agricultural crops without changing the list of these crops. Planning in a broad sense is free from this limitation, but the implementation of such a plan has some peculiarities.

Let us consider the problem of the first type in more detail. Its decision should be preceded by the clarification of yields, presented in the form of production functions from the level of mineral nutrition elements available to plants. At the same time, we assume that the manufacturer has information on the doses of mineral and organic fertilizers, the reserves of easily hydrolyzable nitrogen, mobile phosphorus and exchangeable potassium in the arable layer of the sown areas. Such information, annually replenished and existing in the form of a database, makes it possible to annually adjust the parameters of the named production functions, the analytical expression of which can be specified in the following form:

$y=\frac{b{y}_{max}Q}{y_{max}+bQ}$ (1)

where $Q$ is the pool of food elements available for plants from three sources of absorption: soil reserves, mineral and organic fertilizers, respectively;

$y_{max}$- expert assessment of the maximum possible yield in the given soil and climatic conditions;

- the coefficient of agronomic efficiency, determined by comparing the theoretical yield with the field history data for several past years according to the formula:

$b=\arg \min {\sum }_i{\left\{y_i-\frac{b{y}_{max}{Q}_i}{y_{max}+b{Q}_i}\right\}}^2$ (2)

Where $y_i$,=1,n - yield values of the corresponding crop from the " History of fields" database.

Using the production functions of yields updated for the planned year, we will determine the economically feasible yields of agricultural crops and the corresponding plan for the use of mineral fertilizers. To do this, we will carry out a short-term forecast of sales prices for crop products and prices for production factors that are part of the production cost. This problem can be solved in many ways, the simplest of which is the method of exponential smoothing with parametric adaptation.

Let us return to the problem of substantiating economically viable yields and introduce the following values into consideration:

- sets: agricultural crops, types (names, trade marks) of mineral fertilizers, elements of mineral nutrition of plants, respectively;

${\propto }_{\mathrm{j}\mathrm{k}}$- the content of the active substance of the k-th element of mineral nutrition of plants in the j-th form of mineral fertilizers;

- the number of types of mineral fertilizers from which the plan for their use is formed;

- the active dose of organic fertilizers for the planned year, taking into account the aftereffect;

${\mathrm{\rho }}_{\mathrm{H}\mathrm{k}}$ - the content of the-th element of mineral nutrition of plants in 1 ton of organic fertilizer;

${\mathrm{k}}_{\mathrm{k}}^{\mathrm{S}},{\mathrm{k}}_{\mathrm{k}}^{\mathrm{H}},{\mathrm{k}}_{\mathrm{k}}^{\mathrm{D}}$ - the coefficients of utilization by plants of the–th element of mineral nutrition from soil, organic and mineral fertilizers, respectively;

${\mathrm{p}}_{\mathrm{j}}$ - purchase price of-th type mineral fertilizer, thousand rubles / ton;

${\mathrm{p}}_{\mathrm{i}}$ - selling price of plant growing products of the-th type, thousand rubles / ton;

${\mathrm{z}}_{\mathrm{i}}$ - production cost of the-th agricultural crop, thousand rubles / ton;

${\mathrm{z}}_{\mathrm{i}}^{\mathrm{0}}$ - conditionally constant part of the production cost excluding the cost of the applied dose of mineral fertilizers, thousand rubles / ha (we neglect the changes in the costs associated with harvesting when the NPK doses deviate from those provided for in the basic technology).

The fund of available elements of mineral nutrition of plants is determined in accordance with the following expression:

${\mathrm{Q}}_{\mathrm{i}}=\mathrm{}\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{S}}{\mathrm{V}}_{\mathrm{k}}^{\mathrm{S}}+\mathrm{H}\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{H}}{\mathrm{\rho }}_{\mathrm{H}\mathrm{k}}+\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{D}}\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{M}}{\sum }}{\propto }_{\mathrm{j}\mathrm{k}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$ (3)

where ${\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$ - the required doses of mineral fertilizers of the-th type, containing the-th element of mineral nutrition of plants, applied under the-th agricultural crop;

${\mathrm{V}}_{\mathrm{k}}^{\mathrm{S}}$ - the content of elements of mineral nutrition of the-th type in the soil.

We will write the dependence of the production cost on the dose of mineral fertilizers as:

${\mathrm{z}}_{\mathrm{i}}={\mathrm{z}}_{\mathrm{i}}^{\mathrm{0}}+\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{M}}{\sum }}{\mathrm{p}}_{\mathrm{j}}\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$. (4)

The task of optimizing yield levels is solved in two stages.

At the first stage, the doses of fertilizers ${\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$ are found from the condition of maximizing the specific net income (per 1 ton of production) from the cultivation and sale of N crops of the crop rotation with a budget constraint of W thousand rubles/ha of crop rotation.

At the second stage, the found doses of mineral fertilizers are substituted into the expression for evaluating the stocks of mineral nutrition elements ${\mathrm{Q}}_{\mathrm{i}}$ available to plants and then into the expression for the production function of productivity ${\mathrm{y}}_{\mathrm{i}}={\mathrm{y}}_{\mathrm{i}}\left({\mathrm{Q}}_{\mathrm{i}}\right).$

Thus, we have:

$\underset{\mathrm{i}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{(\mathrm{y}}_{\mathrm{i}}\left(\mathrm{Q}\right){\mathrm{p}}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}})\to \mathrm{m}\mathrm{a}\mathrm{x}$; (5)

${\mathrm{Q}}_{\mathrm{i}}=\mathrm{}\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{S}}{\mathrm{V}}_{\mathrm{k}}^{\mathrm{S}}+\mathrm{H}\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{H}}{\mathrm{\rho }}_{\mathrm{H}\mathrm{k}}+\underset{\mathrm{k}=\mathrm{1}}{\overset{\mathrm{3}}{\sum }}{\mathrm{k}}_{\mathrm{k}}^{\mathrm{D}}\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{M}}{\sum }}{\propto }_{\mathrm{j}\mathrm{k}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$; (6)

$\underset{\mathrm{i}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{\mathrm{z}}_{\mathrm{i}}\le \mathrm{W}$; (7)

${\mathrm{x}}_{\mathrm{i}\mathrm{j}\mathrm{k}}\ge \mathrm{0},\forall \mathrm{i}\in \mathrm{I},\mathrm{j}\in \mathrm{J},\mathrm{k}\in \mathrm{K}$. (8)

The next logical step is to form an optimal crop rotation. Based on assessments of the quality of predecessors in the links of crop rotation, we distribute the sown areas of predecessors according to the crops planned for production. The solution to the problem of crop rotation optimization is based on information about the influence of the predecessor on the yield of the next crop. Information about the influence of predecessors on the yield of the next crop is in the nature of expert assessments of the agronomic service of the manufacturer of the product. The criterion for the quality of crop rotation is also the value of the total net income from the cultivation and sale of commercial crops. The mathematical formulation of the problem is as follows:

$\underset{\mathrm{i}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{{\mathrm{y}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{i}\mathrm{j}}\mathrm{x}}_{\mathrm{i}\mathrm{j}}({\mathrm{c}}_{\mathrm{i}}-{\mathrm{s}}_{\mathrm{i}})\to \mathrm{m}\mathrm{a}\mathrm{x}$; (9)

$\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}={\mathrm{\omega }}_{\mathrm{i}};\mathrm{i},\mathrm{j}\in \mathrm{N}$; (10)

$\underset{\mathrm{i}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}={\mathrm{\omega }}_{\mathrm{j}};$ (11)

$\underset{\mathrm{i}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}\underset{\mathrm{j}=\mathrm{1}}{\overset{\mathrm{N}}{\sum }}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}=\mathrm{A}\mathrm{S};$ (12)

${\mathrm{x}}_{\mathrm{i}\mathrm{j}}\ge \mathrm{0};\forall \mathrm{i},\mathrm{j}\in \mathrm{N}$ (13)

where $y_i$ - the yield of the-th agricultural crop;

${\mathrm{k}}_{\mathrm{i}\mathrm{j}}$ - coefficient reflecting the influence of the-th predecessor on the yield of the-th agricultural crop;

${\mathrm{c}}_{\mathrm{i}},{\mathrm{s}}_{\mathrm{i}}$ - the forecast selling price and production cost of the i-th agricultural crop;

${\mathrm{\omega }}_{\mathrm{i}}$ - sown area of the i-th agricultural crop in the planned year;

${\mathrm{\omega }}_{\mathrm{j}}$ - the sown area of the j-th predecessor in the previous year;

AS - crop rotation area.

Now we can solve the problem of optimizing the sectoral structure of crop production, that is, find the distribution of the entire sown area for cultivated crops from the condition of maximizing net income, taking into account the existing restrictions, resource order: labor and working capital allocated for the purchase of factors of production, as well as for production volumes. At the same time, in the process of solving, there is a distribution of agricultural crops according to technological methods of production, providing for the use of their own seed material or seeds of higher reproductions.

Findings

The solution of the problem under discussion in a broad sense implies the possibility of transforming the sectoral structure of an agricultural enterprise, including by removing some sectors from the economic turnover and replacing them with others. This situation can arise for many reasons:

• from sustainable changes in market conditions to the impact of adverse climatic events. In any case, the structure of the algorithm presented above remains unchanged with the exception of two circumstances:
• the introduction of a new branch of crop production may require additional capital costs for the purchase of specific means of mechanization, the acquisition of technologically conditioned expendable resources;
• the lack of a history of the cultivation of newly introduced agricultural crops does not allow using the apparatus of production functions of yield.

As a result, it will be necessary to introduce adaptive elements for setting up these production functions into the outline of the annual planning system for crop production, and the task of annual planning is preceded by consideration of the corresponding investment project.

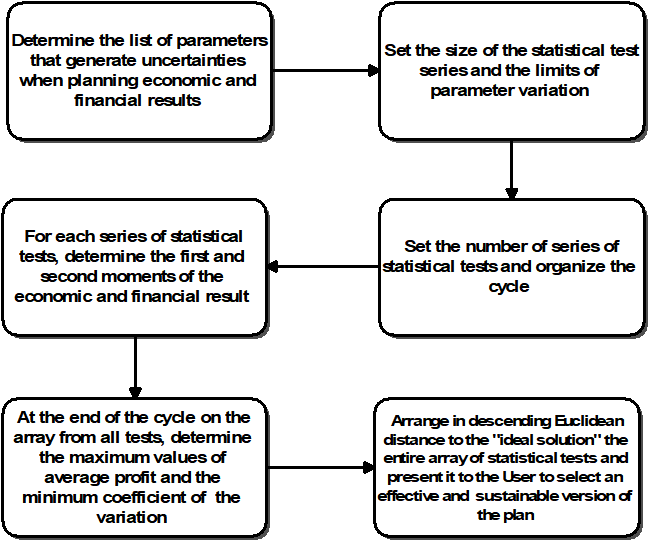
It should also be taken into account that the results of the annual planning algorithm are potentially influenced by a sufficiently large number of parameters arising at different stages of its functioning (short-term price forecasts, expertly set maximum possible yield, soil characteristics, etc.). Of course, the planner focuses on obtaining a cost-effective, risk-based plan. To obtain a stable solution, it is necessary to place this algorithm into a simulation system that implements the plan of experiments in the space of the parameters specified above.

Figure 1 shows a block diagram of such system. The user makes the final choice of the planned option by comparing the indicators of the net income received by him in one or another option and the variance of this indicator, the estimate of which was obtained in a series of simulation experiments.

Let us give an example of the implementation of this algorithm at a conditional agricultural enterprise with the following initial characteristics. The farm produces wheat, sunflower, sugar beet, potatoes and vegetables as commercial crops. Over the past 5 years, the yield of these crops, sales prices and production costs varied within the following limits (Table 1).

See Full Size >

The permissible limits of change in sowing areas were assessed by experts. In the procedure of statistical tests, generators of pseudo-random numbers with uniform distribution laws were used; correlations between the listed features were assumed to be weak.

It was found that for any random combinations of yields, product prices, and its cost, the class of optimal solutions (structure of sown areas) consists of three elements (Table 2).

By the zero (basic) solution we mean the results of statistical tests, when each combination of parameters in Table 1 corresponds to the optimal structure of the sown areas. This option corresponds to the case of full awareness of the future state of parameters that vary in the course of statistical tests.

The results of simulation experiments are presented in table 3.

As is known in the case of two or more criteria, the choice of the plan option, as a rule, remains with the decision-maker. In this case, this choice is almost obvious and does not require the implementation of the “ideal point” procedure stated in the algorithm. This is "Option 2", which is characterized by a slight decrease in profit compared to the base, zero option, and the same insignificant increase in the coefficient of variation. Option 3 with the minimum coefficient of variation generates a profit that is almost 25% less than the base option.

The proposed procedure for assessing the efficiency and sustainability of the functioning of an agricultural enterprise in conditions of uncertainty of the initial information also allows one to give objective assessments of the value of a digital resource. Indeed, the decision "Option 0" is a plan in which the decision on the structure of sown areas is made in conditions of full awareness of the characteristics of a particular year - the person making the decision knows the yield, prices, and costs. In the planned version, due to the fixed structure of sown areas, the variability of profit increases and its average value decreases.

Thus, the value of the digitalization resource can be represented as the ratio of the difference between profits in two versions and the difference between the coefficients of variation. In this methodological example, we obtain a decrease in the variation of profit by 1% due to the procedure of optimal planning, which is equivalent to an increase in the average profit of the farm by 124.1 thousand rubles.

Conclusion

Optimal planning of agricultural production was and remains a rather difficult and not fully resolved task. The relevance of its solution increases as the manufacturer exhausts the main technological capabilities, solving the problems of management accounting. Modern agricultural producers widely use agricultural machinery equipped with sensors and satellite positioning systems, which allows for effective monitoring at all stages of field work. Spot farming technologies are focused on the efficient use of chemicals, coupled with the minimization of environmental damage.

The access to perfect methods of production is obtained mainly by large holding-type commodity producers, the competition between which is increasing. Against this background, many of them began to pay attention to the possibility of obtaining an additional effect from the use of methods of economic and mathematical modeling, accumulating knowledge from different subject areas for systemic application in solving complex problems of planning and management of agricultural organizations, forced to function under conditions of uncertainty: weather - climatic, as well as market. These opportunities are now seen as an effective way of attracting an additional part of the still untapped potential of agriculture.

It should be noted that the arsenal of economic and mathematical modeling is not always fully ready to reflect all the listed challenges. It is for this reason that the authors tried to develop some considerations aimed at improving this promising direction for the development of agriculture in the context of the digitalization of the economy.

Acknowledgments

The article was prepared with the financial support of the Ministry of Education and Science of the Russian Federation under the agreement of December 10, 2019, No. 075-15-2019-1939. Unique project identifier – RFMEFI60719X0302.

References

• Bellman, R., & Dreyfus, S. (1965). Applied Dynamic Programming. Nauka.

• Braslavets, M. E., & Kravchenko, R. G. (1978). Mathematical modelling of economic processes in agriculture. Kolos.

• Csaki, C. (1988). Experiences with agricultural policy models for centrally planned economics Agricultural sector modeling (pp 193–207). Wissenschaftsverlag Vauk.

• Glen, J. J. (1987). Mathematical models in farm planning: a survey. Operations Research, 35(5), 641–666.

• Ognivtsev, S. B., Siptits, S. O., & Hue, C. C. (1997). Modeling of macroeconomic processes in the agricultural sector. VIAPI.

• Romanenko, I. A. (2007). Assessment of investment attractiveness of agricultural organizations. Agrarnaya Nauka, 2, 2–3.

• Romanenkov, V. A., Romanenko, I. A., Sirotenko, O. D., & Shevtsova, L. K. (2004). Soil carbon sequestration strategy as a component of integrated agricultural sustainability policy under climate change Proceedings of Russian National Workshop on Research Related to the IHDP on Global Environmental Change (pp. 180-189). RASHN.