Graphic Method As A Means Of Forming Metasubject Results Of Education

Abstract

The up-to-date Federal State educational standard of basic general education suggests orientation to personal, metasubject, and subject results of education. According to the degree of significance for the student's success in life, metasubject results prevail over subject results, but currently, there are no sufficiently transparent methods for their formation, as well as means for assessing the quality of their achievement. The aim of the work is to investigate the possibilities of the graphic method of solving text tasks as a means of forming metasubject results of education. Solving text tasks plays a key role in realizing that mathematics is not a science disconnected from reality. Every formula can be filled with vital content, and, conversely, you can describe any real phenomena through mathematical models. The study of the interrelationships of different branches of mathematics, in particular, graphic illustration, geometric images, and algebraic expressions teach students to think broadly, to understand the interpenetration of various concepts not only in the field of mathematics but also in other subject areas. As experience has shown, students who have mastered the graphic method show better results in the future and not only in educational activities. They more often take part in research competitions in different subject areas; successfully pass competitive selection in educational institutions of higher education. The graphic method of solving text tasks contributes to students’ intellectual and creative abilities development. This method allows a person to look more broadly at the task that arises both in educational practice and beyond school.

Keywords: Text task, graphic method, metasubject results of education

Introduction

The up-to-date Federal State Educational Standard (FSES) of basic general education is based on the system-activity approach, which involves focusing on f education results (personal, metasubject, and subject). The expected results of education development are highlighted in the approximate basic educational program of basic general education (ABEP BGE) and are presented by subgroups of universal educational actions.

Metasubject results of education include, in particular, students' mastery of intersubject concepts and universal learning activities, as well as the ability to use them in educational, cognitive, and social practice. There are some research works (Chudinsky et al., 2018; Korchazhkina, 2016; Pankova, 2019; Rybakina, 2012; Sergeeva et al., 2017; Testov, 2016) devoted to the study of the components of teaching mathematics content and types of cognitive activity that are metasubject in nature, making the basis for the formation of universal education activities.

Problem Statement

Speaking about the hierarchy of learning results according to the degree of significance for the student's success in life, metasubject results prevail over subject ones. At the same time, the subject teacher understands how to achieve subject results, but the question remains: how are metasubject learning results achieved. The following scientific works are devoted to the possibilities of training future mathematics teachers for the use of metasubject learning technologies (Hodanova, 2016; Perminov & Testov, 2020; Petrova, 2015; Zhuk, 2018). Currently, this problem is due to the contradiction between the need for teaching students to solve life problems in math lessons, and the lack of teachers’ comprehension of how to achieve this by simply solving mathematical tasks. In this regard, students often perceive mathematics as a science that is not related to real life.

Research Questions

The following content components of the subject "Mathematics" that are used to form metasubject results are of great interest, through which it is possible to form schemes of thinking and actions that will allow students to master:

skills of processing information, comparing and analyzing facts,

methods to identify tasks/problems in standard and non-standard situations;

skills of finding an alternative solution;

the ability to ask questions and formulate hypotheses, determine goals, plan, and choose a method of action, control, analyze, and adjust one’s activities.

The subject of this study is such a meaningful component as the graphic method for solving text tasks.

Purpose of the Study

The purpose of the work is to study the possibilities of the graphic method for solving text tasks and for the formation of metasubject results of education.

Research Methods

The research is based on the system-activity and metasubject approaches in education. At the first stage of the study, an analysis of scientific publications was carried out, and to verify the hypothesis experimental work was performed.

Findings

The application of graphs of function to the solution of text tasks is an effective means of achieving, basically, two meta-subject results of education.

1. The ability to create, apply, and transform signs and symbols, models and schemes for solving educational and cognitive tasks.

The key idea is that every formula in mathematics has a practical interpretation. This idea is clearly expressed in the FSES BEP: "The study of the subject area" Mathematics and Computer Science» should provide: awareness of the importance of mathematics and computer science in everyday life; the formation of ideas about mathematics as a universal language of science that allows one to describe and study real processes and phenomena."

Any alphanumeric expression, formula, equation, or function is a description of a real situation. For example, looking at a record $y=200x+5$, you can see not only a linear function or a linear equation with two unknowns but also a real plot. This is a person who is thinking at the ATM about how much cash he needs to withdraw to buy some sweets (the store where his favorite sweets are sold turns out to have no cashless payment). In this equation: 200 is the cost of one kilogram of sweets in rubles, is the weight of the planned purchase in kilograms, 5 is the cost of the package in rubles (he has not taken the package with him, but he needs to buy a lot of sweets), $y$ is the minimum amount that he needs to have to pay for the purchase.

Solving plot tasks plays a key role in understanding this idea (Egupova & Moshura, 2019; Larina, 2016; Roslova, 2017). There is no other way to explain that formulas can be filled with vital content. Formalization of the statement of a text task leads to the appearance of an equation, a system of equations or inequalities, a function or a system of functions, a graphic illustration, which contributes to the formation of such universal educational actions as skills:

create an abstract image of an object and/or phenomenon;

build a model based on the statement of the task and/or the method of its solution;

translate information from a graphic or formalized (symbolic) representation to a text one and vice versa.

2. The ability to independently plan ways to achieve goals, including alternative ones, consciously choose the most effective ways to solve educational and cognitive tasks.

The basic idea is that any mathematical task has several ways to solve it. Mathematics, as a science, has many subsections, being not isolated from each other; they interpenetrate each other and this allows one to study the same objects using different mathematical tools. For example, you can say that $y=200x+5$ an analytical definition of a linear function, and talk about its properties (the domain of definition, monotonicity, and so on), and you can say that this equation describes a straight line on a plane with a Cartesian coordinate system with specified parameters You can study the position of this line relative to the coordinate axes, and after adding another line to the equation $y=200x$, you can talk about their mutual location on the plane. The relationship between these two approaches can be formulated as follows:

* a geometric illustration of such a concept from mathematical analysis as a linear function is a straight line, which leads to the concept of the graph of the function;

* an algebraically geometric object, a straight line that can be described by a linear equation, which leads to the concept of an equation of a straight line on a plane.

Students’ mastering the graphic method of solving text tasks contributes to the formation of such universal educational actions as skills:

justify and choose the most effective ways to solve educational and cognitive tasks;

choose from the suggested options and independently search for means/resources to solve the task/achieve the goal.

Solving tasks by using the graphical method often leads to the need of using geometric facts. Let us illustrate the relationship between the geometric, algebraic, and graphical views of the same phenomenon of uniform motion.

Let us consider the right triangle $ABC$ with the right angle $C$. Figure 1 shows the sides of the triangle as standard $a,b,c,$ and the acute angle $\alpha$.

See Full Size >

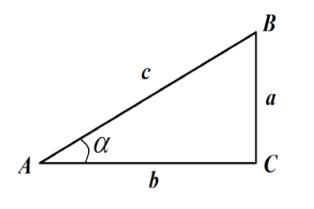
By determining the tangent of the acute angle in the right triangle, it is possible to write the ratio:

$tg\alpha =\frac{a}{b}$(1)

If now the cathet $BC$ is denoted by the letter $S$ in the same triangle and the cathet $AC$ by the letter , the right part of the equality (1) will take the form $\frac{s}{t}$, that suggests the idea of the formula connecting speed, time, and distance with uniform movement:

$\nu =\frac{S}{t}$(2)

See Full Size >

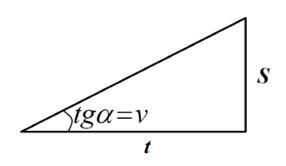
The right triangle becomes a geometric illustration of uniform motion where the tangent of the acute angle represents the speed of movement, the opposite cathet of the acute angle is the distance, and the adjacent cathet is the travel time (See Figure 02).

Formula (2) gives an algebraic model of uniform motion. It can be rewritten differently, expressing one of the three characteristics:

$\nu =\frac{S}{t}$, $S=\nu \cdot t$, $t=\frac{S}{\nu }$.

Assuming one of the characteristics of a known constant in each of the three formulas, we obtain six different functions (four linear and two inverse proportionalities) that express the relationship between the two remaining variable characteristics:

$\nu =\frac{S_0}{t},$ $S={\nu }_0\cdot t,$ $t=\frac{S_0}{\nu }$, $\nu =\frac{1}{t_0}\cdot S,$ $S=t_0\cdot \nu ,$ $t=\frac{1}{{\nu }_0}\cdot S$.

By plotting these functions, we obtain graphical models of uniform motion.

The achievement of the above-mentioned metasubject learning results is realized through such subject results of studying the subject area "Mathematics and Computer Science" as:

mastering the system of functional concepts, developing the ability to use functional and graphical representations to solve various mathematical tasks, to describe and analyze real dependencies;

using the properties of functions and their graphs when solving tasks from other academic subjects;

illustrating a real dependency or process by their characteristics with the help of a graph;

mastering the basic methods of solving plot tasks: arithmetic, algebraic, iteration of options, geometric, graphic and applying them in new situations as compared to the studied ones;

designing and investigating functions corresponding to real processes and phenomena and interpreting the results obtained under the specifics of the process or phenomenon under study;

choosing the optimal method of solving the task and being aware of the choice of the method, considering different methods, and finding different solutions to the task, if possible.

With the help of graphs of function, tasks that describe a certain continuous process: movement, work, filling the hall with spectators, candle burning, etc. are rationally solved. In school tasks, processes are usually described with a constant speed of its flow. Therefore, regardless of the type of process, its characteristics (the speed of the process, the time that is the duration of the process, the result of the process which is the distance traveled, the plowed area of the field, the work performed with unassigned content, etc.) are connected by a linear relationship. This leads to the need for studying the linear function and constructing its graph (Arefieva, 2008). Despite the obvious connection between real processes and mathematical functions, students rarely encounter the modeling of continuous processes in the form of a function in Math lessons; more often they encounter such tasks in Physics lessons. This increases the gap between real-life phenomena and mathematical concepts.

During 2017-2020, several educational programs for schoolchildren of the Jewish Autonomous Region were implemented in Sholom Aleichem Priamursky State University. Within the framework of these programs, teaching text tasks was realized through the graphic method. As experience has shown, students who have mastered the graphic method show better results not only in educational activities in the future. They more often than other students take part in research competitions in various subject areas and successfully pass competitive selection in educational institutions of higher education.

Currently, there are no technologies that allow us to accurately determine the level of formation of metasubject educational results. As a means of evaluating metasubject results of education, a specialized Olympiad in mathematics can be used (Odoevtseva & Kirillova, 2017). Speaking about the search for technologies for monitoring metasubject and learning results, we can resort to the work (Shkerina et al., 2020), which is devoted to defining an approach to monitoring students’ universal learning activities in Maths lessons in 7th-9th grades and obtaining its reliable means.

Conclusion

The graphic method of solving text task contributes to students’ intellectual and creative abilities development. This method allows a person to reveal not only the connection between real processes and mathematical formulas or their models; it allows one to look more broadly at the task that arise both in the educational process and beyond school. Math teachers do not pay enough attention to this method, arguing that it is poorly understood by students. Although, the logical chain is reversed: students do not understand the graphical method of solving maths tasks, because little attention is paid to it.

References

• Arefieva, I. G. (2008). Matematika [Mathematics]. Aversev. [in Russ.].

• Chudinsky, R., Volodin, A., & Bykanov, A. (2018). Studying the Impact of Contextual Data on the Outcomes of the Individual Educational Achievements of the Fourth-grade Pupils While Assessing the Metasubject Results Obtained at the General Education Institutions of Voronezh Region. Proceedings of 5th International Conference on Education, Language, Art and Inter-cultural Communication (ICELAIC 2018): Advances in Social Science Education and Humanities Research, 289, 28-35.

• Egupova, M. V., & Moshura, Yu. V. (2019). O roli zadach na prilozheniya matematiki v dostizhenii metapredmetnykh obrazovatel'nykh rezul'tatov [On the role of the task on the application of mathematics in the achievement of metasubject educational outcomes]. Science and School, 2, 80-88. [in Russ.].

• Hodanova, J. (2016). Modern technology implementation in future mathematics teachers training. Proceedings of 9th Annual International Conference of Education, Research and Innovation: ‏‏ICERI Proceedings. NOV 14-16, 8010-8015.

• Korchazhkina, O. M. (2016). Metapredmetnoye soderzhaniye obrazovaniya vo FGOS obshchego obrazovaniya [The metasubject content of education in FSES of the general education]. Pedagogy, 2, 16-24. [in Russ.].

• Larina, G. S. (2016). Analiz prakticheskikh zadach po matematike: teoreticheskaya model' i opyt primeneniya na urokakh. Voprosy obrazovaniya [Analysis of real-world math problems: theoretical model and classroom application]. Educational Studies, 3, 151-168. [in Russ.].

• Odoevtseva, I. G., & Kirillova, D. A. (2017). Olimpiada po matematike kak sredstvo otsenki metapredmetnykh rezul'tatov obrazovaniya [Olympiad in mathematics as a means of assessing metasubject results of education]. The Perspectives of the mathematical education development in Tver and the Tver region: conference proceedings, 2, 52-54. [in Russ.].

• Pankova, O. A. (2019). Vozmozhnosti uchebnogo predmeta matematika dlya dostizheniya metapredmetnykh rezul'tatov osvoyeniya osnovnoy obrazovatel'noy programmy nachal'nogo obshchego obrazovaniya [Opportunities of mathematics to achieve metasubject results of the basic educational program of primary general education]. Pedagogical Sciences, 3, 28-34. [in Russ.].

• Perminov, E. A., & Testov, V. A. (2020). Modelling methodology as the basis for implementation of an interdisciplinary approach in the training of students of pedagogical specialties. The Education and Science Journal, 22(6), 930.

• Petrova, H. (2015). Formation of metasubject universal skills in students. Pedagogy, 87(4), 533-538.

• Roslova, L. O. (2017). Formirovaniye metapredmetnykh rezul'tatov obucheniya sredstvami praktiko-oriyentirovannykh zadaniy s matematicheskim soderzhaniyem [Formation of metasubject learning results by means of practice-oriented tasks with mathematical content]. Domestic and Foreign Pedagogy, 2, 69-78. [in Russ.].

• Rybakina, N. A. (2012). Formirovaniye metapredmetnykh rezul'tatov obrazovaniya v usloviyakh kompetentnostno-oriyentirovannoy modeli obrazovatel'nogo protsessa. Obrazovaniye i samorazvitiye [Formation of meta-subject results of education in the comprehensive school as the elements of lifelong education]. The Journal of Education and Self Development, 1, 81-87. [in Russ.].

• Sergeeva, M. G., Sinelnikov, I. Yu., & Sukhodimtseva, A. P. (2017). Metasubject abilities development in upper secondary school students as a pedagogical problem. International Conference on Education Environment for the Information Age (EEIA 2017): ‏European Proceedings of Social and Behavioural Sciences, 28, 531-539.

• Shkerina, L. V., Gavrilyuk, A. S., Tabinova, O. A., & Shashkina, M. B. (2020). Bipredmetnyy monitoring rezul'tatov osvoyeniya universal'nykh uchebnykh deystviy obuchayushchimisya 7–9 klassov v protsesse obucheniya matematike. Perspektivy nauki i obrazovaniya [Bi-subject monitoring of the results of mastering universal educational activities by students in 7th-9th grades in the process of teaching mathematics]. Perspectives of science and education, 2, 179-194. [in Russ.].

• Testov, V. A. (2016). O nekotorykh vidakh metapredmetnykh rezul'tatov obucheniya matematike. Obrazovaniye i nauka [Some types of metasubject results when teaching mathematics]. The Education and Science Journal, 1, 4-20. [in Russ.].

• Zhuk, L. (2018). Metodika formirovaniya gotovnosti budushchikh uchiteley matematiki k primeneniyu metapredmetnykh tekhnologiy obucheniya. Nauchno-pedagogicheskoye obozreniye [The technique of formation of readiness of future mathematics teachers to interdisciplinary learning technologies]. Pedagogical Review, 1, 135-141. [in Russ.].