Abstract
In this paper, we consider a modification of the genetic algorithm that affects the stage of formation of a new generation. It is what makes population size dynamically change. Depending on whether there is an improvement in the result of the algorithm in the current generation relative to the previous iteration or not, the population size will either increase or return to the standard one. If there is an improvement, then the size of the population increases, and if not, it returns to its original size. This model uses the change in species abundance in the real biological world. This method is considered in the context of applying to the solution of the problem of forming part of the bank’s loan portfolio, since this business process is poorly automated in commercial banking institutions at a given time. The method was studied and conclusions were drawn on its effectiveness based on the results.
Keywords: loan portfolio, optimization, genetic algorithm, modification, population, dynamics
Introduction
A genetic algorithm is a special case of an iterative algorithm. It is looking for a global extremum of the function and, depending on how many iterations have been performed, the accuracy of the result is increased. The genetic algorithm imitates the evolution of the genotype in the real biological world, working with binary strings. Each iteration of the algorithm consists of several stages - initialization of a new generation, calculation of the fitness function, selection, crossbreeding, mutation, and the formation of a new generation. By modifying the algorithm in various ways, one can get a change in the quality of the result of the algorithm.
The modification of the genetic algorithm described in this paper is considered in the context of applying to the solution of the problem of forming part of the bank’s loan portfolio. Commercial banks regularly receive many loan applications (Partovi, Matousek,2019). The ability of a potential borrower to make loan payments is assessed in special departments of the bank, after which the banking institution raises the question of who approves the loan application and who does not (Yuzvovich et al, 2015, Bojnec, Oliynyk, Adamenko, 2014). For each loan product, the bank has a limited amount of cash resources for its issuance. Also, the bank should not go beyond the general acceptable level of risk of non-payment by borrowers of funds (Gintschel, Hackethal, 2004, Purtikov, 2001). Therefore, only part of the applications is approved for a loan. From which the combination of approved and rejected applications will be selected depends on the income that the bank will receive [6]. However, in most banking institutions, the process of compiling this list is poorly automated and manual.
Problem Statement
The task for which a modified genetic algorithm will be used is to form a list of approved and rejected applications for a specific loan product. For example, to obtain a loan for individuals. The goal is to maximize income from the generated list in the presence of strict restrictions on the amount allocated for the issuance of loans and the permissible percentage of losses from the expected income. Each application includes the interest rate, term, amount for the requested loan and the probability of default by the borrower of its obligations, which are input parameters received from the bank. To formalize the record of the task, the following notation is introduced:
- F – The amount of money allocated for the issuance of loans.
- N – Number of borrowers.
- kj – Loan amount requested by the j-th borrower (j varies from 1 to N).
- tj – The term for which the j-th borrower takes a loan.
- xj – A Boolean variable that takes values: 1 if the loan kj is issued and 0 if the application is rejected.
- dj – Interest for using j-th loan.
- Pj – Probability of default by the jth borrower of obligations to repay the loan and interest on it. It makes sense for the estimated percentage of loan defaults and interest on it. It turns out during the expert evaluation of the application by the bank. In the framework of solving this problem, it is considered in the form of a coefficient obtained as an input parameter.
- ρ – The allowable percentage of losses from the estimated income from all approved loan applications. In the framework of solving this problem, it is considered in the form of a coefficient obtained as an input parameter.
The expected income from a combination of loan applications will be determined by the following formula:
Estimated loss share of income received from all approved loan applications:
Thus, we have a statement of the problem in general form:
These formulas were used to formulate the problem that the modified genetic algorithm should handle.
Research Questions
In this paper, we consider a modification of the genetic algorithm that affects the stage of formation of a new generation. It is what makes population size dynamically change. Depending on whether there is an improvement in the result of the algorithm in the current generation relative to the previous iteration or not, the population size will either increase or return to the standard one. If there is improvement, then the size of the population increases, and if not, it returns to its original size. This model uses the change in species abundance in the real biological world. This method is considered in the context of applying to the solution of the problem of forming part of the bank’s loan portfolio, since this business process is poorly automated in commercial banking institutions at a given time. The method was studied and conclusions were drawn on its effectiveness based on the results.
Purpose of the Study
To solve this problem, it is proposed to use a modified genetic algorithm. It is proposed to modify the stage of formation of a new generation. In the standard genetic algorithm, the population size of each generation is fixed and does not change. It is proposed to make it dynamic. The change in population size during the formation of a new generation will depend on whether there has been a positive change in the best result of the current generation relative to the previous one, that is, whether the value of its fitness function has been increased relative to the previous iteration of the algorithm. If there is an improvement in the result, then it is proposed to increase the size of the population of the new generation, and if there is no improvement, then return the size of the population to the standard value. This approach simulates a change in the population of a species in the real biological world (Semenkin, Kleshkov, 2006, Tynchenko et al, 2018, Rizk-Allah, 2017),
Research Methods
If a species of animals as a result of evolution appears a sign that allows them to better adapt to the environment, then, as a rule, the number of species increases. The described modification can presumably have the following effect on the formation of the final result of the algorithm. The essence of the formation of a new generation in the process of the algorithm is that it is used in the next iteration, going through all stages of the algorithm in order. The new generation is formed from parents, descendants and the best results of the current iteration (Tynchenko et al, 2018, Bakdi, 2018).
The algorithm, in search of a global extremum, calculates the values of the fitness function for each individual - a number in the range from zero to one and performs the process of searching for a global extremum based on this value. Therefore, the more individuals in a new generation of individuals with a higher value of the fitness function, the higher the likelihood that a better solution will be found in the next iteration. And the proposed modification just increases the size of the population if the value of the fitness function of the best result in the current iteration is higher than in the previous one. And if such a condition is met, then this means that individuals of a new generation are more likely to have a higher value of the fitness function. And accordingly, an increase in their number can increase the quality of the algorithm. In other words, if the algorithm goes on the “right path”, then we give it the opportunity to better follow this path, and if it goes astray this way, then on the contrary, let it know about it.For clarity, we can imagine the effect of modification on the result of the algorithm in the form of formulas. We introduce the following notation:
- Pi– The probability of improving the result in the i + 1 iteration.
- Ki – The number of individuals in generation i.
- Fi – The value of the fitness function of the best individual in the i iteration.
- b – The coefficient of dependence of Pi on Pi-1.
- I – Iteration number.
- s – Multiplier of the number of individuals in the population.
Then:
This formula clearly shows what valuesdepends on and whether will increase or decrease when these values change, but it does not show how specifically.The coefficient b is entered in this case to simplify the formula.In this case is introduced to simplify the formula.The modification increases the number of individuals by times if;On the formula, it will look like this:
The formula shows that the proposed modification of the genetic algorithm increases–the probability that a better result will be found in the current iteration than in the previous one, which increases the quality of the algorithm as a whole.
The algorithm can be represented in the form of a flowchart (figure 01).
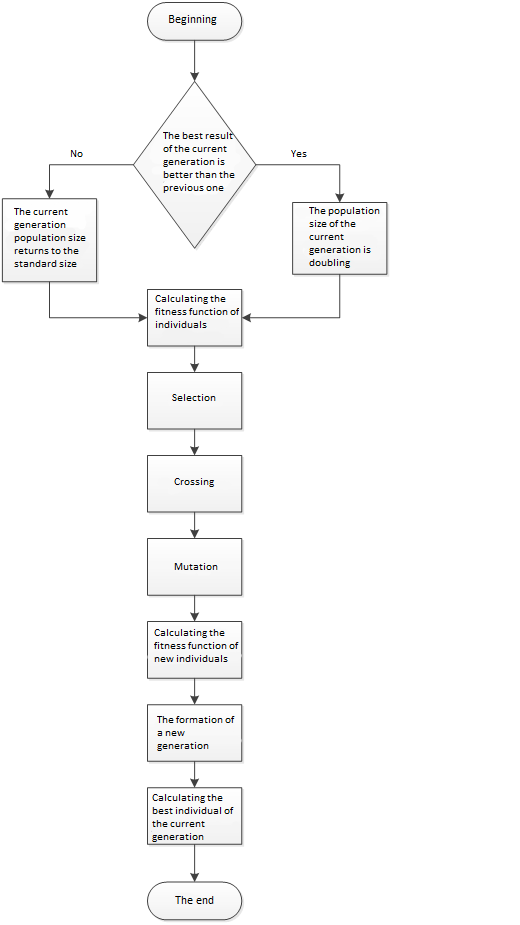
To verify the above assumption, the modification was implemented as an application that solves the problem of forming part of the bank’s loan portfolio (figure 02).
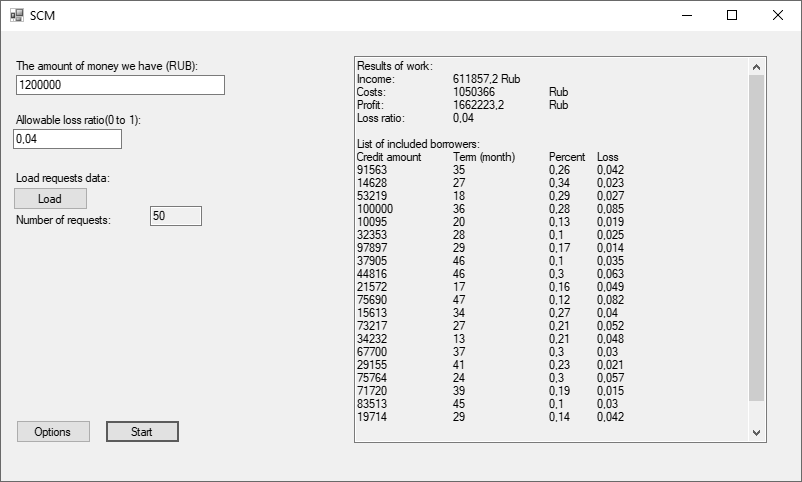
The following data were used as input values (table 01): 1200000rub. - the amount of money allocated for the issuance of loans, 0.04 - the permissible percentage of losses from the estimated income received from all approved loan applications (in the form of a coefficient).
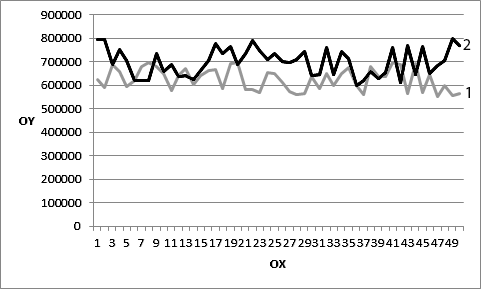
50 runs of the algorithm were tested with and without modification. Each run included 100 iterations (generations). The results are presented in figure 03.
Findings
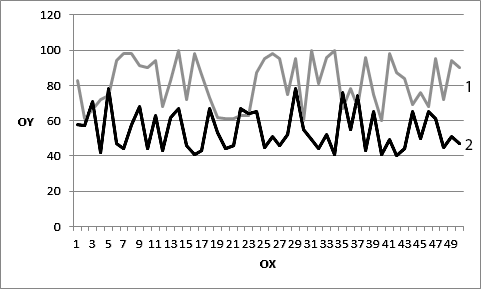
As you can see, the result of the algorithm has become better. A new best solution to the problem was found. A check was also made of starting from which iteration of the algorithm the result ceased to improve. The results are presented in figure 04.
As you can see, the modified algorithm ceased to improve the result of its work earlier than the algorithm without modification. Given that he found better results, we can conclude that he finds the best result faster.
The above approach can be applied to solve the problem of forming part of the loan portfolio of the bank. This problem has a great dimension when it comes to the functioning of real banking institutions, which is the reason for the impossibility of using deterministic mathematical methods to solve it. Since the result of solving this problem will be a list of approved and rejected applications for a loan product, it can be presented in the form of a binary line in which the unit will indicate approval of the loan application, and zero - denial. With this formulation of the problem, the use of a genetic algorithm to solve it is quite convenient and justified
Conclusion
Based on the analysis and testing results of the proposed modification of the genetic algorithm, it was concluded that the use of such a modification can significantly improve the result of the algorithm. Also, the described method is suitable for solving the problem of forming part of a bank's loan portfolio. Its use in this area can significantly increase the income of commercial banking organizations.
References
Bakdi, A., Hentout, A., Boutami, H., Maoudj, A., Hachour, O. &Bouzouia, B.(2017). Optimal path planning and execution for mobile robots using genetic algorithm and adaptive fuzzy-logic control.Robotics and Autonomous Systems. 89, 95-109.
Bojnec, S., Oliynyk, O. O. &Adamenko, V. V. (2014) Credit rationing as a result of optimizing the loan portfolio under the prudent attitude to risk. Actual Problems of Economics.160(1), 437-445.
Gintschel, A. &Hackethal, A. (2004). Multi-bank loan pool contracts: Enhancing the profitability of small commercial banks Applied Financial Economics. 14(17), 1239-1252.
Husin, N. A., Mustapha, N. Sulaiman, M. N.(2013). Hybridization of genetic algorithm and neural network on predicting dengue outbreak. Int.J. on Information Technology (IREIT). 1(2),120-129.
Partovi, E. &Matousek, R. (2019). Bank efficiency and non-performing loans: evidence from Turkey. Research in International Business and Finance.48,287-309.
Purtikov, V.A.(2001)Optimization of the management of the formation of the bank’s loan portfolio. 148.
Rizk-Allah, R. M., Abdel,Mageed, H. M., El-Sehiemy, R. A., Abdel, Aleem, S. H. E. &El,Shahat, A.(2017) A new sine cosine optimization algorithm for solving combined non-convex economic and emission power dispatch problems.Int J Energy Convers. 5(6), 180-192.
Semenkin, E. S. &Kleshkov, V. M.(2006). Models and algorithms for common resources distribution in innovation management of restructured machine building enterprise.Engineering and automation problems. 3, 24-31.
Tynchenko, V. S., Kukartsev, V. V., Boyko, A. A., Danilchenko, Y. V. &Fedorova. N. V.(2018). Optimization of customer loyalty evaluation algorithm for retail company.Advances in Economics, Business and Management Research. 61, 177-182.
Tynchenko, V. S., Petrenko, V. E., Kukartsev, V. V., Tynchenko, V. V. &Antamoshkin, O. A.(2018) Automation of experimental research of waveguide paths induction soldering.IOP Publishing. 1015, 032188.
Yuzvovich, L. I., Tershukova, M .B., Mokeeva, N. N., Zaborovskiy, V. E. &Zaborovskaya, A. E. (2015). Diversification of banking risks in the context of financial globalization. Mediterranean J. of Social Sciences. 6(3S3), 147-156.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
17 May 2021
Article Doi
eBook ISBN
978-1-80296-106-5
Publisher
European Publisher
Volume
107
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-2896
Subjects
Science, philosophy, academic community, scientific progress, education, methodology of science, academic communication
Cite this article as:
Borisovich Sergienko, S., Sergeevich Tynchenko, V., Sergeevna Bets, Y., Igorevna Lytkina, S., Sergeevich Bondarev, A., & Rafinatovna Ogol, A. (2021). Forming Part Of The Bank'S Loan Portfolio With Modified Genetic Algorithm. In D. K. Bataev, S. A. Gapurov, A. D. Osmaev, V. K. Akaev, L. M. Idigova, M. R. Ovhadov, A. R. Salgiriev, & M. M. Betilmerzaeva (Eds.), Knowledge, Man and Civilization - ISCKMC 2020, vol 107. European Proceedings of Social and Behavioural Sciences (pp. 2476-2484). European Publisher. https://doi.org/10.15405/epsbs.2021.05.332
