Theory Of Differential Equations In Forming A Holistic Picture Of The World

Abstract

Research relevance is the need to form a holistic picture of the world in schoolchildren, which, in turn, underlies their personal development. For the purpose to teaching Maths, the elements of the theory of differential equations, being the models of many natural phenomena and processes, can provide a meaningful basis for establishing the relationship of subject content with facts and regularities of the real world. The purpose of the paper is to develop and test theoretical premises and methodological conditions for the effective study of elements of the theory of differential equations as a means of forming a holistic picture of the world based on a practice-oriented approach. The research outcome at this stage is the methodology working0out for teaching senior schoolchildren to solve problems that are reduced to differential equations, which are considered as a testing ground for the development of ideas about the unity and interconnectedness of all components of the surrounding reality. The “advanced” demonstration of the capabilities of mathematical methods for exploring natural science and applied problems while maintaining the logical structure and rigor of the material presentation makes it possible to evaluate the apparatus for solving differential equations as a natural means of systematic study of the real world. The developed methodology for teaching senior schoolchildren to solve tasks reduced to differential equations makes a certain contribution to the methodology of teaching adolescents mathematical sections in the system of supplementary education and contributes to the formation of a holistic picture of the world.

Keywords: Holistic picture of the world, supplementary mathematical education, theory of differential equations, practice-oriented mathematical assignments

Introduction

The concept of “picture of the world” refers to the fundamental scientific categories and is of interest for many areas of scientific knowledge: philosophy, history, cultural studies, philology, psychology, ethnology, etc. Common in understanding a holistic picture of the world is its interpretation as a result of understanding and sensory-emotional assessment of the surrounding reality by a person, and such an understanding that allows finding harmony with the world, understanding the place in it.

Various aspects of the studied issue fell into the field of research interest of scientists throughout the development of pedagogical science: the formation of a holistic picture of the child’s world at the initial stage of education in the pedagogical system of Ushinskii (as cited in Medvedeva, 2009); foundations feasibility of the categorical vision of the world picture and the evolution of the outlook of preschool children (Kulikovskaia & Chumicheva, 2004); peculiarities of schoolchildren worldview at integrated art classes (Shishliannikova, 2017); characteristics and specificity of the formation of the natural science picture of the world (Burova, 1996); formation of an individual information world picture of schoolchildren using computer technologies (Kuzibetskii, 2003) etc.

According to most researchers, the environment and upbringing act as key universal factors in the formation of a holistic picture of the world. Therefore, this process can be characterized as a current change in the way a person interacts with the environment due to an increase in his subjectivity (Chebykina, 2017).

Problem Statement

The formation of a holistic picture of the world is an essential prerequisite for personal development. The formation of unified ideas about the world entails not only qualitative changes in consciousness and personality in general, but also means that a person is able to fully and deeply understand the surrounding world, taking a “proper” place in it. The concepts of the realities of the objective world are becoming more complicated: one phenomenon can be seen and described in different “code systems”, which allows us to see what is hidden and not given in direct sensation and perception. A holistic picture of the world acts as the coordinate system that determines the direction of a person’s activity, his priorities in life, activity, and creativity (Medvedeva, 2009).

It is impossible to form a holistic picture of the world among senior students in the conditions of a contemporary school without entering the system of supplementary education. Certain aspects of the surrounding world are studied within the framework of isolated subjects, when it is impossible to illustrate their unity in the conditions of a chronic shortage of educational time within the walls of a comprehensive secondary school. Each academic discipline claims its significance in the context under consideration but cannot provide a completely systematic description of the surrounding reality, and only represents some of its “facets”. Accordingly, the problem of subject content selection arises for the most effective formation of a holistic picture of the world among senior students. In modern conditions, this pedagogical problem takes on a new meaning. Its relevance is dictated by new requirements for the educational system, the constantly updated social order of community.

Research Questions

Mathematical content plays a special role in the formation of a holistic picture of the world, since many tasks from different areas of knowledge and practical activity of a person are solved by creating one or another universal mathematical model (Rodionov & Dedovets, 2018; Rodionov et al., 2018). It follows the significance of solving practice-oriented issues by senior students, providing mastery of the mathematical modeling method. Besides, the needs of senior students for professional self-determination are met in this way.

The theory of differential equations acquires great importance in the context under consideration (Dalinger & Simonzhenkov, 2008; Filippov, 2004; Lobanova, 2016). This value is determined by the fact that the most general laws governing the physical world, since the time of Newton and Laplace, are formulated in the form of differential equations. Differential equations describe the motion of planets in the solar system, the rotation of a whirligig, the motion of electrons in an atom, electrical oscillations in a radio generator, wave distribution and many others. Calculation of the artificial satellite motion, the computation of a nuclear reactor, and the behavior of a ship when rolling or a bridge under the action of a dynamic load requires the application of differential equations. Differential equations are essential in any case when it is required to study unevenly flowing processes, that is, processes in which the change rate of the quantities varies over time or depends on the values of the quantities themselves. It is commonly known that many issues on geometry, mechanics, physics, hydraulics, aerodynamics, heat engineering, resistance of materials, the theory of elasticity, electrical engineering and other sciences are reduced to them, systematically reflecting various sides and entities of the surrounding world.

Purpose of the Study

The purpose of the paper is to develop and test a methodology for studying the elements of the theory of differential equations as a means of forming a holistic picture of the world based on a practice-oriented approach.

Research Methods

It is necessary to ensure the continuity and consistency in teaching the appropriate educational material between the basic and additional training courses, considering the opportunity of studying the elements of the theory of differential equations in the system of supplementary education. In any case, students get the potential to naturally expand knowledge on a specific educational challenge, gradually supplementing and adjusting their ideas about the surrounding reality (Ammosova, 2005; Ammosova & Krasnova, 2012).

Analysis of school textbooks, FSES and teacher guide books shows that the material about the simplest differential equations is covered in the course of the school curriculum on Mathematics. In particular, schoolchildren interfere with the results of integrating a differential equation in the ninth grade when considering uniformly accelerated motion. The elements of differential and integral calculus, the beginnings of which are studied in senior grades of a comprehensive secondary school, are closely related to differential equations. The practical application of methods of the theory of differential equations in the senior grades is implemented in the physics course. A clear understanding of the derivative as a function that expresses the relationship between specific physical quantities is formed among senior students when solving elementary differential equations and tasks reduced to differential equations. The material about differential equations is included in the corresponding course in studying on the physical and mathematical profile, providing future applicants with a successful continuation of their studies in higher educational institutions.

A number of determinants should be taken into consideration when defining the content and nature of the material presentation of the theory of differential equations in the system of supplementary education:

1. The specified material should not duplicate the university course; it must be of practice-oriented nature and, at the same time, include the elements of pronounced novelty for senior students.

2. It is advisable to pay special attention to the humanitarian component development of mathematical education (history of mathematical discoveries, the origin of terms and symbols, fragments from the life of mathematicians, etc.).

3. It is required to ensure the full implementation of the schoolchildren's vigorous activity, contributing to the progress in their mental operations, methods of reasoning, and creative initiatives.

The main didactic tasks of the corresponding supplementary course are:

• formation of senior students’ ideas about the role of differential equations in solving various issues of the surrounding reality;
• ensuring the assimilation of the conceptual apparatus of the proposed theory;
• teaching students to solve selected types of differential equations;
• disclosing the possibilities of applying differential equations to the construction of models of practice-oriented tasks, in particular, formalization of practical issues and a qualitative interpretation of the obtained solution outcomes.

Findings

It is important to motivate senior students at the first stage of studying the material. In particular, this is facilitated by the students’ speeches prepared in advance with the help of the teacher, which show by examples that the solution of the considered tasks is reduced to one or several equations containing, in addition to the variables and the required functions, the derivatives of these functions in various fields of science (natural science, medicine, biology and others), as well as in technology and mechanics. These equations are called differential.

Furthermore, senior students are told what concepts and types of differential equations, as well as their applications in science and practice, they will get acquainted in the course of classes. The following scheme (as shown in Figure 1) is proposed for studying the elements of the DE (differential equations) theory in SE (supplementary education) institutions considering the amount of knowledge available to schoolchildren, including knowledge of the geometric and physical meaning of the derivative.

See Full Size >

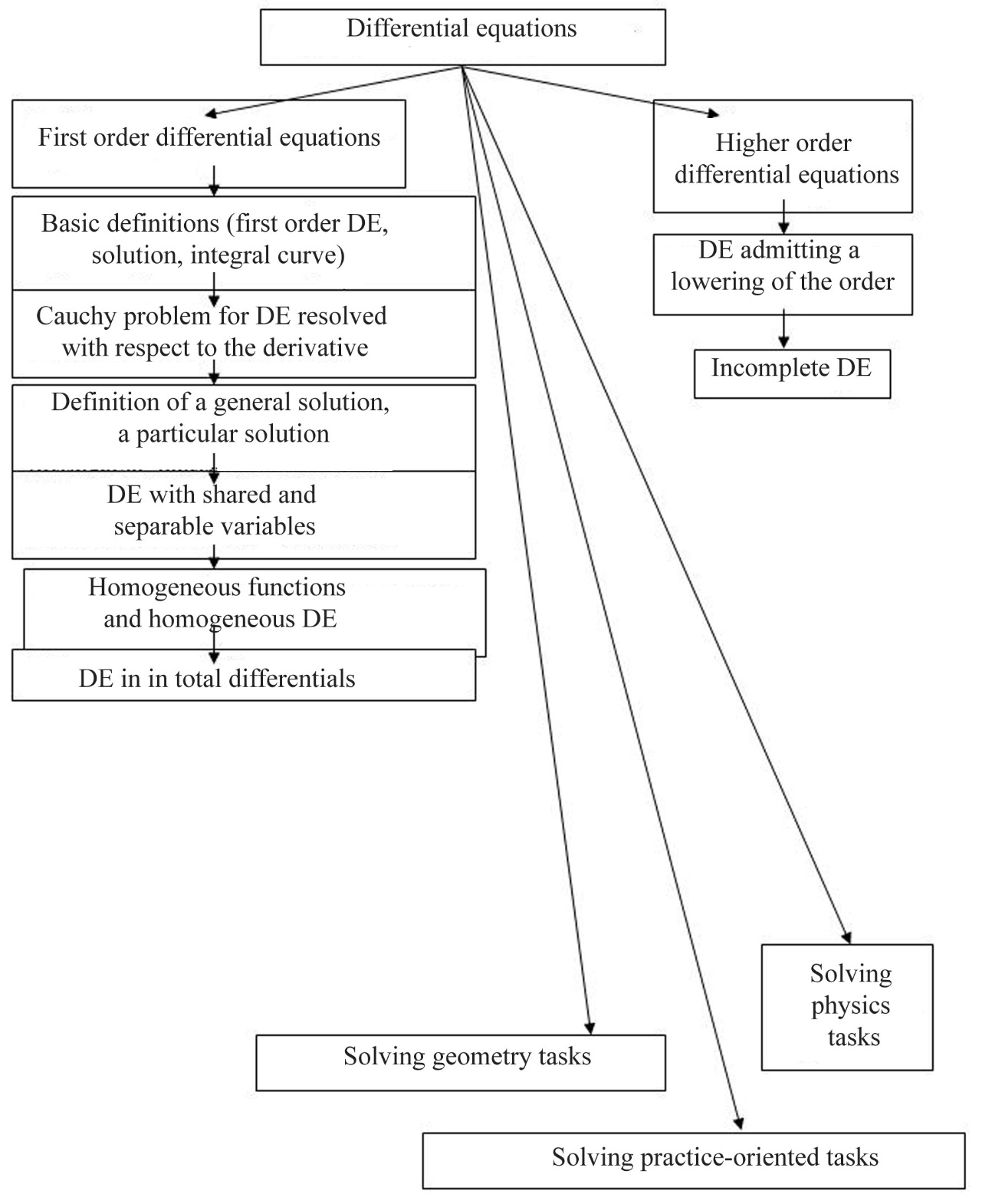
Experience shows that the given volume of material on the theory of differential equations, based on school knowledge, makes it possible to demonstrate the possibility of its application in solving geometric, physical, and economic and other kinds of problems, thereby, contributing to the students' minds formation of a unified worldview, and a holistic picture of the world.

The next stage of studying the course implies the study of the conceptual apparatus study of the DE general theory. Students, with the help of a teacher, formulate a solution definition to a differential equation as a function that turns this equation into true equality by analogy with the algebraic equations theory studied in the framework of the basic school course.

Senior students should realize that the theory of differential equations is a direct development and deepening of the material of differential and integral calculus. The solution to any practice-oriented problem is reduced to a differential equation and consists of two stages: creative (making up a differential equation), and technical (solving a differential equation). In this regard, it is essential to develop both the ability to compose such an equation and teach students feasible methods for solving selected simple classes of equations (with separable variables, homogeneous equations, total differentials, etc.).

At this stage, senior students master the concepts of an ordinary differential equation, the order of a differential equation, a general, particular and special solution of a differential equation, an integral curve, a family of integral curves and their envelope.

The given concepts are updated in the course of solving problems, such as:

We give an example of such an issue, which has wide application in physics:

Example 1. Consider natural oscillations that occur without friction and resistance, then according to Newton’s second law = –.

Considering that acceleration is the second time derivative of the path

$m\frac{d^{2}x}{d{t}^2}=-kx$, we divide both sides of the equation by t.

$m\frac{d^{2}x}{md{t}^2}+\frac{k}{m}x=0$, indicate $\frac{k}{m}=w_0{}^2$, where $w_0^2$ – is a natural oscillation frequency. We obtain $\frac{d^{2}x}{d{t}^2}+w_0^{2}x=0$– the equation of the trajectory of natural oscillations without friction and resistance is a second order differential equation. Its solution is $x=A_0\mathrm{S}\mathrm{i}\mathrm{n}\left(w_{0}t+f_0\right)$ – a harmonic oscillation equation.

Each student draws up a concept map of new learned notions, which is subsequently analyzed and generalized. The most acceptable version of such a map is developed in the consequence of collective discussion.

It is advisable to start the direct study of equations with separable variables, since this type is familiar to schoolchildren within the framework of the curriculum in a comprehensive secondary school. The natural transition to their generalization is due to differential equations with shared variables. They include the following five types of differential equations, and mastering the method of solving them is carried out using examples of the corresponding tasks:

1. An equation of the form $y^{\mathrm{\text{'}}}=f\left(x\right)$ that does not (explicitly) contain the desired function.

2. An equation of the form $y^{\mathrm{\text{'}}}=f\left(x\right)$ that does not (explicitly) contain an independent variable.

3. An equation of the form $y^{\mathrm{\text{'}}}=f\left(x\right)g\left(y\right)$ or $\frac{dy}{dx}=f\left(x\right)g\left(y\right)$, in which the right side is the product of a function that depends only on, by a function depending only on.

4. An equation of the form: $M\left(x\right)N\left(y\right)dx+f\left(x\right)g\left(y\right)dy=0$.

In the above cases, it was indispensible to multiply both sides of the equation by the same expression to obtain an equation with separable variables. This characteristic is familiar to students, since it is used to solve algebraic equations (quadratic, irrational, fractional rational, symmetric, etc.). In the following case, students will need to use the method of replacing the expression with a new variable. They also used the method during Mathematics lessons in a comprehensive secondary school; therefore, most schoolchildren can handle them well.

The task material considered at this stage, students partly solve in the classroom, and partly in an individual format – in the course of independent work.

At the next stage, senior students move on to solving homogeneous differential equations based on the concepts of a homogeneous function and the order of homogeneity. After working out this concept, the definition of a homogeneous differential equation is considered in the form:

$\frac{dy}{dx}=f\left(\frac{y}{x}\right)$

It is advisable for the teacher to draw the attention of schoolchildren to the naturality and expediency of replacing the fraction y/x with a new variable.

It is also useful to acquaint senior students with the representation of a fraction as a sum of elementary fractions by the method of indefinite coefficients, in order to demonstrate the close relationship between various mathematical sections. This method is quite accessible, since all the actions used in it (reduction to a common denominator, combining similar terms, equating the corresponding terms of monomials, etc.) have long been known to students. Teachers should only try to avoid very cumbersome transformations.

Knowledge of equations in total differentials requires students to understand the concept of a function of two variables and partial derivatives, which have not been studied before. Students are offered the familiar circle equation:²+² =². It can be differentiated in various ways:

1) resolve with respect to:= $\sqrt{r^{\mathrm{2}}-x^{\mathrm{2}}}$ and find the derivative: $\mathrm{}y\mathrm{\text{'}}=\mathrm{}\frac{-\mathrm{2}x}{\mathrm{2}\sqrt{r^{\mathrm{2}}-x^{\mathrm{2}}}}$ = $\frac{-x\mathrm{}}{y}$ ,

2) find the derivative of implicit function: 2′ + 2′ = 0 and considering that′ = 1, we obtain:′ = $\frac{-x\mathrm{}}{y}$,

3) consider as a function of two variables:² +² –² = 0,(,) =² +² –²,(,) = 0, then′ = 2′ + 2′ = 0, where y′ = $\frac{-x\mathrm{}}{y}$.

Based on the latter case, the teacher introduces the concept of differentials of the function u (x, y) with respect to the variables x and y, as well as the total differential of the function u (x, y), which is written as follows:.

Further, the teacher trains students in finding the partial derivatives of functions of two variables and their total differentials.

The equation is defined in total differentials, the solution method of which is illustrated by the example of specially selected tasks.

The next stage is devoted to considering the simplest cases of lowering the order of the differential equation.

The considered incomplete differential equations of the second order are easily reduced to equations with shared variables, and the simplest of them students begin to solve when studying the basic school course.

All the studied types of differential equations in the framework of the course under consideration are illustrated on tasks with real content. We give an example of such a task.

Example 2. Establish the relationship between the variable mass of a flying rocket and flight speed.

The solution is based on the known physics law and the derivative and differential concepts.

Let the mass of the rocket at some point is equal to, the gas flow rate is denoted by, and emitted over the time particles mass. In this case<0, as the mass of the rocket decreases. For the time the rocket will lose weight in the amount of fuel equal to –. Suppose that due to this, the rocket receives an increment in speed. The increase in the momentum of the rocket massis equal to, and the momentum of the emitted gases is. Based on the law of momentum conservation, we have:=–, and this is the differential equation. By simple transformations of the equation, we obtain a formula that is of fundamental importance in current rocket technology: $\mathrm{}\frac{dm}{m}=-\frac{dv}{c}$, whence $m=A{e}^{-\frac{v}{c}}$. Suppose that₀ is the rocket mass before flight, at=0. Then₀ and $m=m_0{e}^{-\frac{v}{c}}$. Thus $v=c\mathrm{l}\mathrm{n}\frac{m_0}{m}$ is the formula of K.E. Tsiolkovsky, the basic one for calculating the rocket movement.

It can be determined during the discussion that the obtained formula is suitable only for an airless space in the absence of the action of gravity. Accounting for air resistance and gravity makes the differential equation much more complicated. The equations arising in the calculation of space launches are very complicated and can be solved onlyby dint of the corresponding packages of mathematical programs.

The answer is $=c\mathrm{l}\mathrm{n}\frac{m_0}{m}$ .

Similar assignments related to tasks of a search nature demonstrate the process of drawing up differential equations, by solving which a senior student has the opportunity to obtain a function describing the real situation and allow solving other issues of the physics course.

Conclusion

Consideration of the material on differential equations in the conditions of supplementary mathematical education, the “advanced” demonstration of the possibilities of mathematical methods for studying natural and applied problems, while maintaining the logical structure and rigor of the material presentation, makes it possible to achieve that the abstractness of mathematical concepts and research methods will be perceived by schoolchildren as a basis for systemic study the real world and its regularities.

The developed teaching materials were used in the practice of MISE “Center for extracurricular activities in Zelenokumsk, Sovetskii district”, and a number of schools in the Stavropol Territory for 5 years. According to the experience, the study of the selected types of equations, on the one hand, does not reveal any particular difficulties for senior students who are interested in mathematics and master the mathematical apparatus in the volume of secondary school.

On the other hand, the inclusion in the corresponding curriculum of practice-oriented task material on the indicated topics brings novelty to the educational process. Moreover, it provides an opportunity to form ideas about the unity and integrity of the world around them, the variety of possibilities for its presentation for senior students.

References

• Ammosova, N. V. (2005). Some aspects of training mathematics teachers to work in the system of supplementary education for schoolchildren. Science of Kuban, 174–179.

• Ammosova, N. V., & Krasnova, G. G. (2012). Implementation of continuity in teaching mathematics in primary and high school (on the example of studying equations). Siber. pedagogical J, 252–256.

• Burova, L. I. (1996). Formation of the initial system of knowledge about nature in primary schoolchildren “Pedagogy and methods of primary education”. Prometei.

• Chebykina, E. M. (2017). Formation of a holistic picture of the world among junior schoolchildren at “The World Around” lessons. Yekaterinburg.

• Dalinger, V. A., & Simonzhenkov, S. D. (2008). Modelling with differential equations. LLC PPC “Sfera”.

• Filippov, A. F. (2004). Introduction to the theory of differential equations. URSS.

• Kulikovskaia, I. E., & Chumicheva, R. M. (2004). Technologies for the formation of a holistic picture of the world in preschoolers. Pedag. Society of Russ.

• Kuzibetskii, I. A. (2003). Formation of a personal information picture of the world of senior students using computer technologies of education. Volgograd.

• Lobanova, N. I. (2016). Elements of the theory of differential equations in the system of supplementary education. Internet-journal World of Sci. http://mir-nauki.com/PDF/32PDMN616.pdf

• Medvedeva, N. G. (2009). Formation of a holistic picture of the world in a child at the initial stage of education in the pedagogical system of K.D. Ushinskii. Kursk.

• Rodionov, M., & Dedovets, Z. (2018). Developing students' motivation for learning through practical problems in school. Advances in Science, Technology and Engineering Systems, 3(5), 258-266.

• Rodionov, M. A., Fedoseyev, V. M., & Dedovets, Z. (2018). Specifics of designing a technological component in an integrated methodological system of mathematical training of future engineers. Integrat. of Ed., 383–400.

• Shishliannikova, N. P. (2017). Formation of a living perception of the world among younger students by means of art. Bull. of Buryat State Univer. Pedag. Philol. Philos., 121–125.