Methods Of Assessing The Competitiveness Of Machine-Building Enterprises

Abstract

The economic development is one of the priorities any country. The efficient development of business strategies in enterprises aims to ensure a growing product and meet demand. The present study analyzes possibilities of economic activization due to its balanced development using efficient programs of economic growth incoprporating all possibilities of the current economic state of large businesses and calculation of risk aversion using methodology for assessing the competitiveness. The method for business strategy development takes into account all the evaluation parameters the competitiveness. Under a restricted admissible market balance, the method is reasonable. The model improves efficiency of business resource management. An integral index gives an idea of the use of resources in terms of their availability and allows controlling their efficient development. If resources are limited, additional ones can used. The presence of a state of competitiveness in a machine-building enterprise or the ability to achieve the necessary level of competitiveness in the near future predetermines the need to assess the stability of this state.

Keywords: Functionstrategycompetitivenessmachine-buildingplanning

Introduction

The machine-building complex is one of the leading industries in the world. Mechanical engineering includes a large number of sub-sectors.

It consists of the production of equipment for metallurgical plants, technological equipment for light and food industries, automobiles, aircraft, machine tools, tractors, equipment, etc. Mechanical engineering is related to labor productivity, materials consumption, energy intensity of gross domestic product, the safety and defence of the state (Schupletsov, Klipin, & Skorobogatova, 2018).

On today, prospects for the development of the machine-building complex are very pessimistic. This is due to the increase in the activities of other sectors of the Russian economy, which are active consumers of engineering products. It is not always advisable to consider the purchase of machine-building products from foreign manufacturers as an alternative. As practice we shows, that the cost of domestic analog costs the consumer much cheaper (Barteisman, Scarpetta, & Schivardi, 2005).

Currently, the investment policy of machine-building enterprises formed in negative conditions. It is investment climate (heterogeneity, variability and instability). Investment image has a significant impact on the investment attractiveness of the Russian machine-building industry.

The existing problems in investing need solved immediately. It is necessary to formulate and justify those integral indicators that would allow qualitatively and quantitatively assess the effectiveness of investment policy in machine-building enterprises.

It is necessary to determine the competitiveness of industrial organizations for further investment (Porter, 2001).

We decided to create a system of indicators for assessing competitiveness. It is requirement of systematic adaptation of competitiveness indicators to the working conditions of economic systems at different levels (Porter, 2003).

In the course we analyzed methods, where the set of indicators is focused on reduction to some integral criterion. For visualize the reality, we used a method that boils down to the allocation of significant quantitative indicators and their integration.

Problem Statement

In our opinion, it is necessary to assess the competitiveness of industrial enterprises through a method based on the use of the desirability function (Beregova & Klipin, 2017).

This method will allow to some extent to simulate the process of coordinated behavior of individual subsystems of a single whole, to take into account the connections and impacts between them. It scheme presented on figure 01 .

See Full Size >

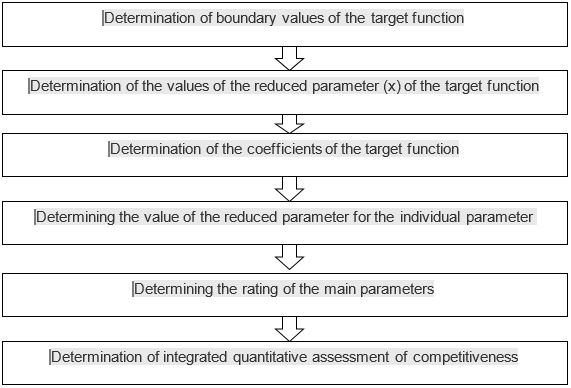
The considered method possesses characteristics necessary for us. Method include theoretical validity, system of estimates, sufficient level of formalization, completeness of the account of factors, level of approbation in practice of estimation.

Research Questions

We calculated of the integral index of assessing the level of competitiveness of engineering enterprises is carried out on the model 1:

$$\mu =\sqrt[n]{{\prod }_{\mathrm{1}}^n{f}_i}\left(1\right)$$

where $\mathrm{n}$ – the number of estimated levels of competitiveness of an industrial enterprise; $f_i$ – i -th level of competitiveness.

It consists of the following parameters: $f_{factor}$ – factor competitiveness; $f_{management}$– competitiveness of the management; $f_{product}$– competitiveness of products.

Factor competitiveness characterizes the aggregate competitiveness of functionally interrelated areas and is determined by model 2

$$\mu =f_{inov}\bullet n_{\mathrm{1}}+f_{prod}\bullet n_{\mathrm{2}}+f_{ecol}\bullet n_{\mathrm{3}}+f_{pers}\bullet n_{\mathrm{4}}+f_{econ}\bullet n_{\mathrm{5}}+f_{fin}\bullet n_{\mathrm{6}}+f_{soc}\bullet n_{\mathrm{7}}+f_{mark}\bullet n_{\mathrm{8}}\left(2\right)$$

$f_{innovation}$ – innovative competitiveness; $f_{production}$ – production competitiveness; $f_{economic}$ – economic competitiveness; $f_{financial}$ – financial competitiveness; $f_{market}$ – marketing competitiveness; $f_{personal}$ – personal competitiveness; $f_{social}$ – social competitiveness; $f_{ecology}$– environmental competitiveness.

Numbers in the model (2) – weighting factor, calculated on the basis of a priori considerations.

For assessing we used functional area of competitiveness. Area choose specialists and managers of different levels of industrial enterprises, representatives of the scientific community are involved.

Evaluation of each component $f_i$ it is carried out according to the model of the target function presented in the form of a model (3):

$$f_i=\frac{\mathrm{1}}{\sqrt[e^x]{e}}\left(3\right)$$

where $e$ – the base of the natural logarithm; $x$ – the given value of the investigated parameter.

The basis of the construction of this function is the idea of converting the natural values of private indicators into a dimensionless scale of the target function. Each actual calculated value of the target function is given a specific economic meaning. It is related to the level of competitiveness of the enterprise. Moreover, the value of the desirability function equal to 0 corresponds to an unacceptable level of the parameter (Rodrigues, 2010). The value of the desirability function equal to 1.00 corresponds to a completely acceptable level of the parameter, or such a value of the parameter at which further improvement in the framework of solving specific tasks is impractical or impossible. Intermediate values of the desirability function, their economic characteristics relative to the competitiveness of industrial enterprises or functional areas of its competitive advantage are given in table 01 .

In case of change of external or internal conditions of functioning of the machine-building enterprise the statement of a problem can change.

To perform further calculations and graphical constructions it is necessary to obtain the values of the given parameter $\left(x\right)$ and to give the indicators characterizing functional areas of competitiveness – ( $p_i$), to the values of the given parameter ( $x)$objective function $f\left(x\right)$. To do this, the rules presented by the formulas are introduced and used (4) and (5):

$$p_i=p_i\left(x_i\right)=\left\{\begin{array}{c}\mathrm{0},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}if\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}p\mathrm{}\le min\\ \frac{(p-min)}{(max-\mathrm{m}\mathrm{i}\mathrm{n})},\mathrm{}if\mathrm{}\mathrm{}\mathrm{}\mathrm{}min<p\le max\\ \mathrm{1},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}if\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}max<p\mathrm{}\end{array}\right.\left(4\right)$$

Or

$$p_i=p_i\left(x_i\right)=\left\{\begin{array}{c}\mathrm{0},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}if\max <p\\ \frac{(max-p)}{(max-\mathrm{m}\mathrm{i}\mathrm{n})},\mathrm{}if\mathrm{}\mathrm{}\mathrm{}\mathrm{}min<p\le max\\ \mathrm{1},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}if\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}min\le p\mathrm{}\end{array}\right.\left(5\right)$$

where $p_i$ – the given values of the indicator $p$ to the values of the reduced parameter ( $x_i$); $p$ – the current value of the criterion; $min$ – minimum value of the criterion $p$; $max$ – maximum value of the criterion $p$;

The results are summarized in table 02 .

Obtained value ( $x)$и ( $p_i$) in the interval of the target function allow to model descriptive dependencies. It acts as an approximating function in the form of a linear dependence: $x=a\bullet p+b$. The coefficients of the model equation are determined by the formulas (6) and (7):

$$a=\frac{x_{\mathrm{2}}-x_{\mathrm{1}}}{p_{i,n\mathrm{2}}-p_{i,n\mathrm{1}}}\left(6\right)$$

$$b=\frac{{p_{i,n\mathrm{2}}\bullet x}_{\mathrm{1}}-p_{i,n\mathrm{1}}\bullet x_{\mathrm{2}}}{p_{i,n\mathrm{2}}-p_{i,n\mathrm{1}}}\left(7\right)$$

where $x_1$ and $x_2$ – values of the target function in the interval; $p_{i,n1}$ and $p_{i,n2}$ – the values of the parameters of the objective function.

The calculated values of the approximation coefficients are presented in table 03 .

On the basis of the received dependences the reduced value of parameter x is calculated and the target function for each considered parameter is defined. The main results of the calculations are summarized in table 04 . An example of calculating the final value Of the Harington desirability function characterizing the level of competitiveness of an industrial enterprise operating in the territory of China. The results indicate a satisfactory level of competitiveness, but with the presence of trends in its growth in the future.

The presence of a state of competitiveness in a machine-building enterprise or the ability to achieve the necessary level of competitiveness in the near future predetermines the need to assess the stability of this state.

Purpose of the Study

The purpose of this research is to increase the competitiveness of high-tech industrial enterprises. This research allows us to develop a model of competitiveness of high-tech industrial enterprises. As part of the research, a tool for assessing the level of competitiveness of high-tech industrial enterprises was developed.

Research Methods

In the study, we used the following scientific methods: economic and mathematical modeling, statistical analysis, economic analysis, qualitative and quantitative assessment, system and institutional approaches, generalization and comparison, construction of logical chains and links to justify the conclusions in the work.

Findings

This article presents a model of the system for ensuring the competitiveness of high-tech industrial enterprises. This model consists of three levels. The first level characterizes competitiveness based on 5 functional areas (technological, human resources, social, marketing and financial and economic competitiveness), the Second level forms factor competitiveness. At the second level, competitiveness is ensured through a competitive management system for a high-tech industrial enterprise. The third level determines the competitiveness of products. The dynamic relationship of these areas on three levels forms stable chains of interaction.

Conclusion

The proposed method allows to analyze business processes in the company. Top management can identify weaknesses and develop an effective development strategy. It should be noted that this technique will help to find and apply effective ways of distribution of cash flows, attraction of foreign investments. In our opinion, this will lead to a multiplier effect in related industries.

Acknowledgments

The authors acknowledge receiving support from state-funded research program of Irkutsk National Research Technical University. We are responsible for all errors as well as heavy style of the manuscript.

References

1. Bartelsman, E., Scarpetta, S., & Schivardi, F. (2005). Comparative analysis of firm demographics and survival: evidence from micro-level sources in OECD countries. Industrial and corporate change, 14(3), 365-391.
2. Beregova, G. M., & Klipin, A. O. (2017, June). Analysis and assessment of economic state of enterprise in context of strategy of import substitution. In International Conference on Trends of Technologies and Innovations in Economic and Social Studies 2017. Atlantis Press.
3. Polzunova, N. N. (2012). System of regional management of competitiveness of machine-building enterprises: theory and methodology. Vladimir.
4. Polzunova, N. N. (2013). Analytical tools for assessing the competitiveness of business structures using high technologies. Economical analysis: theory and practice, 32(335), 30.
5. Polzunova, N. N. (2017). Organizational and economic mechanism to ensure the competitiveness of high-tech industrial enterprises. Moscow: Energoizdat.
6. Porter, M. E. (2001). Regions and the New Economics of Competition. In A.J. Scott (ed.) Global City-Regions. Trends, Theory, and Policy (pp. 145–151). New York: Oxford Univer. Press.
7. Porter, M. E. (2003). The Economic Performance of Regions. Reggression Studies, 37, 549–578.
8. Rodrigues, M. (2010). Import substitution and economic growth. Journal of Monetary Economy, 57, 175–188.
9. Schupletsov, A. F., Klipin, A. O., & Skorobogatova, Y.A. (2018). Formation of model of import substitution in machine-building complex. European Proceedings of Social and Behavioural Sciences, 50, 1071–1077.