Abstract
The problem of the management of the implementation of regional socio-economic programs considered. Significant implementation time, characteristic of this type of programs, requires, after each stage of their adjustment, due to both a change in the socio-economic situation in the region and possible mismatch between the planned and actual results of the previous stage. The purpose of the work is to develop tools to support for managerial decision-making to determine the system of requirements for the projects, intended for implementation at the next stage of the socio-economic program in the face of uncertainty and risk. The methodological apparatus of multi-criteria expert assessment, game theory and artificial intelligence theory are used as the theoretical foundations of the developed toolkit. The developed procedure includes a survey of experts (which allows determining the results of the last stage of the program and clarifying the required targets for the next stage), drawing up a decision-making task (forming a list of strategies and possible situations, as well as expert evaluation of the results of applying strategies in relevant situations), choosing a managerial decision (based on the Hurwicz criterion in determining the coefficient of pessimism /optimism using a system of linguistic variables, the system fuzzy production rules and the fuzzy inference algorithm of Mamdani). The approach proposed in the work allows taking into account the specifics of the regions and increase the scientific feasibility of managerial decisions made in the process of implementing socio-economic programs.
Keywords: Socio-economic programdecision-makinguncertainty
Introduction
The uneven socio-economic development of the regions is one of the most significant factors of instability in the world, stimulating negative processes, ranging from social, national and religious extremism to environmental degradation of territories caused by the use of outdated industrial technologies.
The effective mechanism for managing the socio-economic development of regions is the development and implementation at the regional level of specialized national programs. For example, in the Russian Federation, such federal target programs as “Development of Education”, “Housing”, “Integrated rural development”, and others are currently being implemented. As part of these programs, regional authorities form their own regional development programs in these areas, taking into account their specifics (Telegin, 2018). This regional specificity is to some extent taken into account by the federal target programs aimed at the socio-economic development of territories uniting several regions (for example, the program “Protection of Lake Baikal and the Socio-Economic Development of the Baikal Natural Territory for 2012–2020”), but this is the same. Individual regions have their own characteristics, which should be reflected in the relevant regional programs.
Problem Statement
Despite a significant number of fundamental works devoted to the general problems of sustainable development of regions (for example, Blewitt, 2015; Tausch, 2012), as well as to some special legal issues (Rakhmatullin, 2019), organizational (Malikova, 2017), financial (Poltarykhin, Ryabova, Minaeva, & Malsagov, 2019) support and assessment of progress (Firov, 2018; Khusainova & Bakhvalov, 2018) of regional socio-economic programs, regional authorities in their practice, often face problems when making organizational decisions, e.g. particular an effective and science-based management of the implementation of these programs. This is due to the insufficient level of methodological research for practical use and (as a result) the lack of effective decision support tools for managing regional programs, taking into account the uncertainty and risk that are characteristic of the subject area.
Research Questions
The construction of decision support tools in the form of uncertainty and risk in relation to the task of managing the implementation of programs requires the study of two interrelated issues
Multi-criteria expert evaluation of results of previous stage and plans for next stage
The adoption of managerial decisions on program management should be based on reliable (to the extent necessary) information regarding both current and predicted (as a result of the next stage of the program) socio-economic situation in the region. One of the main sources of this information (along with reporting statistics for the past period and the results of predictive modeling) is a survey of experts (highly qualified specialists in the subject area) (Zotov, 2019). At the same time, it is necessary (in relation to the task of evaluating programs) to consider the issues of planning, conducting and processing the results of the survey that significantly affect the final result.
Statement and solution of the problem of game theory, according to the choice of strategy in the implementation of the next stage
The choice of strategy on the basis of which a managerial decision will be made on the implementation of the next stage of the socio-economic program is proposed to be carried out using the game theory methodology of incomplete information (Harrington, 2008). In this case, it is necessary to investigate issues related to the formation of the game matrix and the construction of a selection criterion. The use of the Hurwicz criterion (as proposed in the work) leaves it necessary to study the method for determining the coefficient of pessimism /optimism included in the criterion formula. In the framework of the proposed approach, this coefficient, which is very significant for solving the problem, is determined on the basis of expert judgments, the processing of which is carried out using the Mamdani fuzzy inference algorithm (Mamdani, 1974).
Purpose of the Study
The purpose of the work is to develop tools to support for managerial decision-making to determine the system of requirements for the projects, intended for implementation at the next stage of the socio-economic program in the face of uncertainty and risk.
Research Methods
The methodological apparatus of multi-criteria expert assessment, game theory and artificial intelligence theory are used as the theoretical foundations of the developed toolkit.
Findings
The proposed selection procedure (from the set of possible options
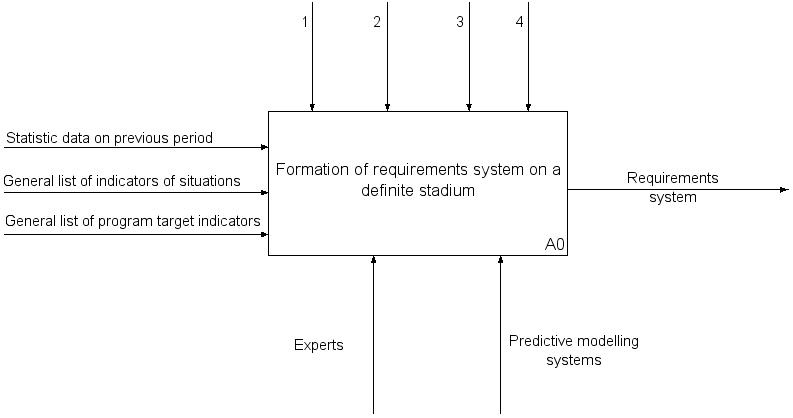
In Figure
1 – domain knowledge principles;
2 – regulation documents;
3 – multi-criteria expert assessment methods;
4 – game theory and artificial intelligence methods.
The decomposition diagram of the process under consideration is presented in Figure
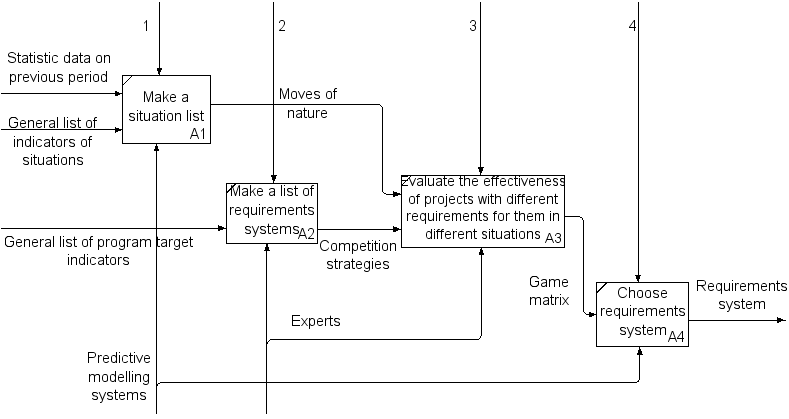
Uncertainty the choice of a system of requirements is associated with the unknown socio-economic state of the region at the next stage of the program. Predictive modeling can give only possible situations from a certain list
Here,
Let
The semantics of the verbal values (terms) “low” and “high” of these variables, as well as the linguistic variable
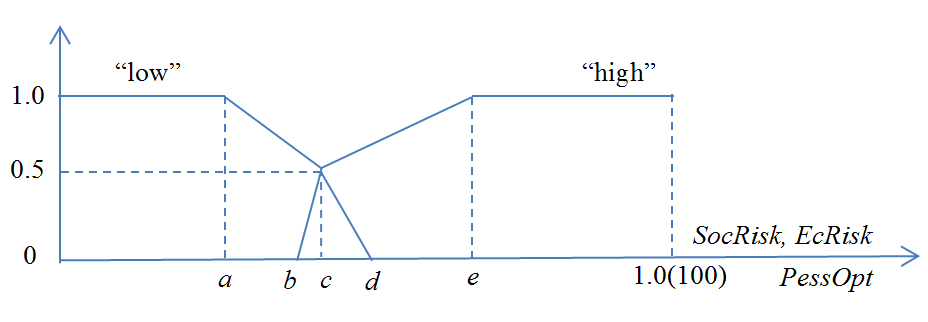
In Figure
The relationship between the variables
R1: if (((
R2: if ((
After fuzzification of numerical values expressed in points (obtained as a result of a survey of experts) of linguistic variables
Conclusion
The approach proposed in this work to solving the problem of supporting managerial decision-making for managing regional socio-economic programs, based on the integration of multi-criteria expert assessment methodologies, game theory and fuzzy logic, allows taking into account the high level of uncertainty inherent in the subject area under consideration. The procedure developed on the basis of the proposed approach includes interviewing experts, formalizing the task of choosing a set of requirements for projects to be implemented at a later stage, in the form of a game with incomplete information, and also solving a game based on Hurwicz criterion with a coefficient defined on the basis of fuzzy inference of pessimism / optimism.
The practical significance of the results is determined by the possibility of using the constructed procedure in the development of information and analytical support for the work of the competition commissions for the selection of projects for the next stage of the program. Moreover, to select the project that best meets the found requirements, multi-criteria hierarchical selection procedures can be used, for example, Analytic Hierarchy / Network Process (Saaty, 2008). More complex is the task of not adjusting, but of synthesizing a complex of projects to be implemented (in accordance with certain requirements) at subsequent stages. Due to the large number of options in this case, it will be necessary to use a special methodological apparatus (for example, evolutionary models and methods for the intelligent synthesis of discrete systems (Lomazov, Petrosov, Dobrunova, Lomazova, & Matorin, 2016; Petrosov, Lomazov, Dobrunova, Matorin, & Lomazova, 2015), which may serve as a direction for further research.
Acknowledgments
The reported study was funded by Russian Foundation for Basic Research, project number 20-07-00855.
References
- Baganov, V. Yu. (2019). The main aspects of decision making under uncertainty. Azimuth of Science Research: Economy and Management, 8(2), 54–58.
- Blewitt, J. (2015). Understanding Sustainable Development, 2rd ed. London: Routledge.
- Firov, N. V. (2018). On the issue of substantiating socio-economic programs and plans, analyzing the course and evaluating the results of their implementation. Question of the reg. economy, 2(35), 68–75.
- Harrington, J. E. (2008). Games, strategies, and decision making. New York: Worth Publ.
- Khusainova, S. V., & Bakhvalov, S. Yu. (2018). A regional system to forecast the social-economic development: the case of the RF regions. European Research Studies J.ournal, XXI(1), 588–601.
- Lomazov, V. A., Petrosov, D. A., Dobrunova, A. I., Lomazova, V. I., & Matorin, S. I. (2016). Evolutionary selection of the models of interacting processes on the basis of expert assessments. International Journal of Applied Engineer. Research, 11.3, 1867–1873.
- Malikova, E. S. (2017). The principles of the formation of programs of socio-economic development of municipalities. Bulletin of the Voronezh Institution of Economy and Social Management, 4, 30–31.
- Mamdani, E. H. (1974). Application of fuzzy algorithms for control of a simple dynamic plant. IEE Proceedings D: Control Theory and Applications, 121(12), 1585–1588.
- Naydis, O. A., & Naydis, I. O. (2018). Collective methods of solving non-standard tasks: comparative analysis. Azimuth of Science Research: Economy and Management, 7(3), 206–209.
- Petrosov, D. A., Lomazov, V. A., Dobrunova, A. I., Matorin, S. I., & Lomazova, V. I. (2015). Evolutionary synthesis of large discrete systems with dynamic structure. Bioscience Biotechnology Research Asia, 12(3), 2971–2981.
- Poltarykhin, A. L., Ryabova, T. F., Minaeva, E. V., & Malsagov, M. I. (2019). Methodical platform for the development of socio-economic programs in the region. Financial economy, 4, 527–530.
- Rakhmatullin, R. R. (2019). Problems of legislative support of economic development strategies. Jurisprudence, 3, 10–12.
- Saaty, T. L. (2008). Relative Measurement and its Generalization in Decision Making: Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors – The Analytic Hierarchy/Network Process. Rev. of the Royal Spanish Academy of Science, Series A, Mathematics, 102.2, 251–318.
- Tausch, A. (2012). Globalization, the Human Condition, and Sustainable Development in the Twenty-first Century: Cross-national Perspectives and European Implications. With Almas Heshmati and a Foreword by Ulrich Brand. London: Anthem Press.
- Telegin, Zh. A. (2018). Regional features of the formation of programs of social and economic development of rural areas. Agriculture Economy of Russia, 3, 75–79.
- Zadeh, L. A. (1965). Fuzzy Sets. Information and Control. 8, 338–353.
- Zotov, V. B. (2019). Guidelines for the development of programs for the socio-economic development of municipalities using expert methods. Municipal Academy, 1, 111–119.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
07 December 2020
Article Doi
eBook ISBN
978-1-80296-095-2
Publisher
European Publisher
Volume
96
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-833
Subjects
Management, human resources, resource efficiency, investment, infrastructure, research and development
Cite this article as:
Lomazov, A. V., Lomazov, V. A., Akupiyan, O. S., Nehotina, V. S., & Rumbesht, V. V. (2020). Support For Managerial Decision-Making In Implementation Of Regional Socio-Economic Programs. In A. S. Nechaev, V. I. Bunkovsky, G. M. Beregova, P. A. Lontsikh, & A. S. Bovkun (Eds.), Trends and Innovations in Economic Studies, Science on Baikal Session, vol 96. European Proceedings of Social and Behavioural Sciences (pp. 404-410). European Publisher. https://doi.org/10.15405/epsbs.2020.12.53

