Practice-Oriented Approach To The Study Of Differential Equations In High School

Abstract

The article discusses the technique of introducing senior students to the concept, types and methods of solving differential equations in the framework of further education. The relevance of this study is due to the need: – to teach high school students the solution of practical problem situations using mathematical methods using practice-oriented problems and existing mathematical education almost eliminating this. The result of the study is a developed method for teaching older students to solve problems (especially practice-oriented), which are reduced to differential equations, namely, learning to find a way to solve a problem, apply a mathematical modeling method, ways to solve the resulting differential equation of a certain kind, and critical reflection of the result. The developed technique for teaching older students how to solve problems, which are reduced to differential equations, makes a definite contribution to the methodology for teaching older adolescents in mathematical sections in the system of additional education. The presented methodology was tested in practice and approved by the methodological association of teachers of the system of additional education in Zelenokumsk, Stavropol Territory of Russia, at a meeting of the Department of Mathematics and its teaching methods at Astrakhan State University, as well as by the scientific and pedagogical community at conferences where the results of the study were reported. Using the presented methodology allows teachers of the system of additional education to achieve efficiency in the process of familiarizing high school students with the principles of the theory of differential equations.

Keywords: Additional educationhigh school studentsmethodsdifferential equations

Introduction

Modern society requires highly qualified specialists with a research position, able to solve problems arising from the needs of the practice in professional activities (Rodionov, Fedoseyev, Dedovets, Shabanov, & Akimova, 2018). This leads to the need to use mathematical methods in non-mathematical situations, one of which is the method of mathematical modeling. The training of professionals demanded by society begins at school (Rodionov & Dedovets, 2018). The study of the problem of introducing high school students to solving differential equations, which are models of practice-oriented problems, and methods for solving problems that reduce to differential equations, is relevant in the context of the Federal Educational Standard. Existing scientific and methodological studies of the problem do not cover a wide range of issues. For example, they do not study the issues of teaching schoolchildren the method of mathematical modeling – one of the main in mathematics, the solution of practice-oriented (and geometric) problems through differential equations, and, moreover, the available studies do not apply to the system of additional education.

Meanwhile, the solution of many vital (economic, technical, scientific and other) problems leads to the necessity of using mathematical modeling by means of differential equations. In the school course of mathematics, the substantive line of equations is one of the main ones. We study linear, square, rational and fractional rational, irrational, logarithmic, exponential, trigonometric equations and systems of equations, including those with parameters. The tasks from this section of school mathematics are included in the exam paper. High school students implicitly encounter elements of the theory of differential equations, for example, in a physics course in the 9th grade when considering uniformly accelerated motion. Therefore, differential equations can be considered as the next stage in the development of the "Equations" line, especially since there are corresponding prerequisites for this.

The school programs on algebra and the principles of analysis provide for the study of all necessary sections of differential and integral calculi, which allows you to directly go on to study the elements of the theory of differential equations and through them to mathematical modeling of real phenomena and processes that occur in everyday life.

One of the possible solutions to this problem is to apply a practice-oriented approach to student learning. The basis of the practice-oriented approach in education is a rational combination of fundamental education and vocational training. According to the Federal State Educational Standard of Education, the disclosure of mathematical laws in living nature, the demonstration of the interconnections between mathematics and art, and practical areas of activity is one of the main tasks of practice-oriented teaching of mathematics at school. The implementation of the practice-oriented approach allows us to remove the aggravated contradiction between the need for students to master the system of vital, practically demanded knowledge and skills, the development of their creative abilities and the insufficient study of practice-oriented teaching and its educational capabilities, since practice-oriented education, in contrast to traditional, focused on the assimilation of knowledge, is aimed at acquiring, in addition to knowledge, skills, also practical experience activities.

Elements of the theory of differential equations are readily understood by high school students. The study of differential equations based on the geometric and physical meanings of the concepts of derivative and integral is a natural continuation of the study of the school discipline "Algebra and the beginning of mathematical analysis."

Differential equations are of great applied value; they are widely used in mathematics, natural sciences, economics, and other fields of knowledge. Thanks to elegant solution methods, concrete and clear applications of differential equations, there is every reason to expect that their study will cause keen interest in high school students.

When solving practice-oriented tasks, interdisciplinary relationships are established, since the setting of tasks covers all areas of knowledge and all branches of human activity. Therefore, we can talk about pre-profile training for high school students, who are given the opportunity to get acquainted with the practical tasks of different areas of professional activity of a person: medicine, pharmaceuticals, ecology, etc.

Problem Statement

The relevance of this study is due to the need: – to teach high school students the solution of practical problem situations using mathematical methods using practice-oriented problems and existing mathematical education almost eliminating this, – to acquaint them with modern research methods with the aim of understanding the world around, in particular, the method of mathematical modeling, and the almost complete absence of this in the practice of the school, as well as the insufficient amount of time allocated within the school ogrammy on familiarity with senior solution of differential equations and, especially, practically oriented tasks using differential equations, and the presence of this time additional education system (Rodionov, Akimova, & Shabanov, 2017).

Research Questions

Since there aren’t enough hours for this in the educational time of a comprehensive school, it is advisable to implement methods for solving differential equations on the basis of a practice-oriented approach in the framework of further education. The implementation of the interaction between general school education and additional in terms of educational activities, expanding the mathematical horizons, familiarizing yourself with areas of mathematics directly adjacent to the school course, including differential equations and their applications, is very productive. The interconnection of teaching mathematics in a comprehensive school and in the framework of additional education acts as a means of implementing the didactic principles of continuity, continuity and systematicity, leading to the integrity of students' knowledge.

The work of a number of researchers is devoted to the organization of additional education for schoolchildren; these studies affect only the pedagogical side the problem under consideration.

Methodological aspects of studying the theory of differential equations (concept and ways of its implementation, methodological system, applied orientation) are reflected in Aslanov (1997), Dalinger and Simonzhenkov (2008) and others. Let's consider this direction in more detail.

Methodological aspects of teaching differential equations are reflected in the books and studies of Aslanov (1997), Bavrin (1998), Dalinger and Simonzhenkov (2008), Lvov (2009), Melnikov (2007), Naimanov (1992), Plotnikova (2000) and others.

Gerbekov (1991), one of the first on the basis of a systematic approach and professionally-pedagogical orientation of training, built the concept of studying differential equations in a pedagogical university and pointed out the ways of its implementation in the process of teaching students: specific recommendations on propaedeutic work, on the selection of task material, on the organization of educational process, etc.

A special place is occupied by the doctoral dissertation of Aslanov (1997), in which a methodological system for teaching differential equations in a pedagogical university is developed that maximally realizes the humanitarian potential of this course. In the study, the course of differential equations is considered not as a section of the course of mathematical analysis, but as an independent discipline.

In the works of Bavrin (1998) and Naimanov (1992) investigated the applied orientation of the course of differential equations in a teacher training university. The book of Dalinger and Simonzhenkov (2008) is devoted to the problem of modeling by means of differential equations. Melnikov (2007) developed a methodological system that integrates fundamental and applied components in teaching differential equations to future physics teachers.

All of these studies played an undoubted positive role in teaching differential equations and their applications, but only in relation to students of pedagogical universities. Only in the works of Lvov (2009), Plotnikova (2000), Sycheva (2013) considers the teaching of differential equations for students of technical universities. An important role in the section "Differential Equations" is assigned to applied problems, since they serve as a means of establishing a connection between mathematics and the professional component of education, in particular, between mathematics and general technical and special disciplines.

In the process of working with applied mathematical problems, which are reduced to a differential equation, it is possible, without involving professional information, to form skills in students related to the study of mathematical models, which will be in demand both in the study of general technical and special disciplines, and in future professional activity, since the ability to research a mathematical model provides an opportunity to study the phenomenon as a whole, to predict its development, to make quantitative measurements occurring in it over time, which in turn allows the development of professional propaedeutics based on solving applied problems on the subject of "Differential Equations". All these studies have played an undoubted positive role in teaching differential equations and their applications, but only in relation to university students, pedagogical and technical.

Meanwhile, in all school textbooks, the concepts of the derivative and the integral, the geometric and mechanical meanings of the derivative are considered. We note that the integrals are considered only in the simplest and in a limited number. However, there are all the prerequisites for a successful more detailed familiarization of high school students with ordinary differential equations and their application to solving practical problems.

Among the studies devoted to the study of differential equations with students, we note Polekhina (1996), which examines the study of differential equations with high school students. It developed a methodology for solving equations based on the unity and difference of methods for solving algebraic, transcendental and differential equations. Polekhina (1996) presented the author's optional course on the topic "Differential Equations" for classes with an in-depth study of mathematics, in which the study of differential equations is considered as the final stage in the development of the line of equations in school. Note that in the dissertation under consideration, the author explores the problem of studying differential equations with high school students, but only in classes with in-depth study of mathematics, does not consider this problem in relation to a comprehensive school, and even more so, to the system of additional education (Polekhina, 1996), does not introduce students to with the method of mathematical modeling, does not stop in detail on solving geometric problems by the method of differential equations, does not adhere to a practice-oriented approach, ho In the aggregate of the tasks she cited, there are problems with practical subjects.

Thus, the available scientific and methodological studies of the problem do not cover the whole wide range of issues. For example, they do not study the problems of studying differential equations in a comprehensive school, and even more so, in the system of additional education, teaching schoolchildren the method of mathematical modeling – one of the main in mathematics, they do not consider teaching schoolchildren solving practical problems through differential equations in the system of additional education , no attention is paid to the establishment of intersubject communications (geometry and algebra and the beginnings of analysis) by solving geometric problems problems by the method of differential equations.

As you can see, despite the fact that the school curriculum in mathematics creates good propaedeutics for studying differential equations and solving practical problems that reduce to them, the problem of studying differential equations in an additional education system based on a practice-oriented approach using a mathematical modeling method requires further development.

Purpose of the Study

The aim of the study is to consider the application of a practice-oriented approach to the study of differential equations in the framework of further education.

Research Methods

In the process of research were used:

• work on the teaching methodology of the theory of differential equations

• research in the application of a practice-oriented approach and the implementation of the applied orientation of mathematics in teaching;

• works devoted to the methodological aspects of the application of the method of mathematical modeling;

• studies on the organization of training of schoolchildren in the system of additional education;

• The theory of activity and its application to the learning process;

• methodological aspects of the compilation and use of problems in teaching mathematics in high school.

Theoretical methods: a comparative analysis of scientific, pedagogical, educational and methodical literature aimed at determining the content and logic of research; the study of normative documentation for teaching mathematics in secondary school, the system of additional education.

Empirical methods related to the study of teaching practice in further education: diagnostics of the state of knowledge of students with the help of tests and tests, pedagogical observation, interviews, questionnaires, interviews, study and generalization of the practice and experience of secondary school mathematics teachers and additional education teachers, analysis of their own teaching experience, conducting an experiment.

Statistical methods: statistical processing of research results, the use of chi-square criteria to assess the validity of the hypothesis formulated.

Findings

In modern conditions, it is especially important to organize the learning process so that its educational result is manifested in the development of its own internal motivation for learning, thinking, imagination, creativity, sustainable cognitive interest of students, in the formation of a system of vital, practically demanded knowledge and skills, which allows students to adapt to life and treat it actively, creatively. One possible solution to this problem is to use a practice-oriented approach to learning. An important role in the study and assimilation of new mathematical abstractions is played by the solution of practice-oriented problems, which serve as a stimulating motive for their study and cause interest in these abstractions.

Practice-oriented training is a didactic approach that is universal in nature. It allows you to eliminate functional illiteracy in the field of using the mathematical apparatus, performs a coordinating role in the development of content and teaching technology, determines the ratio of theoretical and practical in teaching, changes the attitude of students to the studied discipline, meets the requirements of today. Practice-oriented training is a type of training whose primary purpose is the acquisition of new knowledge and the formation of practical experience in their use in solving specific vital tasks and problems. It ensures the inclusion of subject knowledge in the system of value knowledge, freely functioning in human life. The learning process in the framework of a practice-oriented approach is an informative creative process in which learning activities for students are successful and knowledge is in demand. This is facilitated by a system for selecting the content of educational material, which helps students assess the significance and practical relevance of acquired knowledge and skills. In a practice-oriented educational process, not only the life experience of the students is used, but also a new experience is formed on the basis of newly acquired knowledge. Students should learn some specific activity not according to textbooks and drawings, but directly included in its simplest forms.

An analysis of the interpretations of the concept of “practice-oriented approach” by the authors allowed us to give its refined wording. By a practice-oriented approach to teaching high school students the elements of the theory of differential equations in an additional education system, we mean integrated learning: – including not only solving problems of practice-oriented content, but also conducting laboratory and practical work, organizing excursions, using concept maps, workbooks, – Developing understanding by schoolchildren of the importance of mathematical methods, in particular, the method of mathematical modeling, for solving vitally important problems lovechestva problems – prepares them for direct involvement in the future professional activity.

Continuity and consistency in learning allow us to resolve the contradiction between the need to form an integrated system of mathematical knowledge, skills and the discrete nature of the study of educational material (Ryzhakov, 1999). Continuity in the content of mathematical training appears as a continuous process of developing the structural components of content, a smooth transition from one stage of learning to another, a gradual complication of the content of educational information, a gradual change in the level of requirements for the volume and depth of assimilation of knowledge and skills (Ammosova & Krasnova, 2012). In this case, each subsequent stage of the educational system is a natural continuation, development of the previous one, which is typical for the spiral arrangement of material, and high school students have the opportunity to gradually and continuously expand their knowledge on a particular educational problem, avoiding gaps (Ryzhakov, 1999).

The purpose of students studying mathematics in additional education is to expand and deepen the knowledge they gained during the study of the school course, to develop the abilities and skills of students in combination with general education, to generate interest in mathematics at the initial level, and to maintain it at a cognitive level.

It is known that in mathematics, as a rule, the study of new concepts takes place on the basis of already known concepts, the solution of new problems often comes down to already solved known problems. The mathematical task contributes to the formation of certain forms of thinking necessary for the development of reality surrounding us, as it studies concepts introduced by abstracting from the phenomena of the real world (Ammosova, 2005). A major role in the study and assimilation of new mathematical abstractions is played by the solution of practice-oriented problems, which act as a stimulating motive for their study and arouse interest in these abstractions. In this regard, the teacher needs to train students in the ability to analyze the problem situation, consider it from different angles, without losing sight of the whole, highlight various aspects and connect them together, that is, develop relevant mental operations (Ammosova & Krasnova, 2012; Rodionov & Velmisova, 2008).

Analyzing the problems associated with solving equations in the school course of mathematics, academician Anosov (2001) noted that probably the most important and most common problems of this kind are differential equations, and although they are clearly not present in the school course of mathematics, the simplest examples of differential equations are found in the school course of physics. Elements of the theory of differential equations are quite accessible for students of 11th grade to understand, since this requires only an understanding of the meaning of the concepts of derivative and integral, initial skills to differentiate and find primitive, simplest integrals, and this is just provided for in the school curriculum. Therefore, the study of differential equations is a natural continuation of the study of the discipline "Algebra and the beginning of mathematical analysis", based on the geometric and physical meanings of these concepts. Age features of high school students are sensitive to the assimilation of this material, since, according to psychologists, the older teenager is quite stable in their interests, capable of long-term mental work, he is interested in the professional orientation of the material studied, he begins to consider the world from the point of view of how it can be changed and what place in it he himself would like to take.

Differential equations are of great practical importance; they are widely used in mechanics, physics, astronomy, and in many problems of biology and chemistry. There is a need and expediency of teaching schoolchildren to solve differential equations and problems arising from practice that can be solved using differential equations. For this, there is quite enough time in the system of additional education, while in the framework of compulsory secondary education, time is not allocated for the study of this material. In addition, in the framework of further education, there will be time for excursions and other active methods of studying the elements of differential equations and their applications.

Practice-oriented tasks show students the connection between the processes and phenomena of the real world and its mathematical models. The method of mathematical modeling is one of the most commonly used methods for studying real world situations, which is used to solve practical problems. Bringing students to the development of the three main stages of mathematical modeling (compiling a mathematical model; solving a problem by mathematical means; translating the result into the language in which the considered problem was written) is an important task for an additional education teacher.

For successful study by high school students of the elements of the theory of differential equations, it is necessary to rely on the knowledge available to students and their subjective experience, therefore, information and methods of activity known to students should be activated. To this end, it is necessary to organize propaedeutic activities with high school students.

To systematize mathematical knowledge, it is advisable for students to compile conceptual maps, with the help of which connections are established between new concepts and already known ones. Thus, the interconnectedness of concepts is achieved, their hierarchical structure is established, intersubject communications are traced, and the students' knowledge becomes integral, they form an idea of the unity of the world. Conceptual cards help the imaginative presentation of the main ideas of the topic.

 In addition, conceptual maps provide an easy way to assess the quality of students' understanding of fundamental concepts of the theory of differential equations, such as the equation allowed and not resolved with respect to the derivative, the general solution and the particular solution, the general integral and the partial integral, the integral curve, the initial condition, the problem Cauchy et al.

The concept map includes a number of nodes and arrows. Nodes correspond to important terms in the subject (concepts). The arrows indicate the relationship between a pair of concepts (nodes), talk about how these two concepts are related. The connection between the concepts is represented on the conceptual map by a combination of two nodes and an arrow.

Previously, the most used concepts related to the topic of the course should be selected for the development of conceptual maps. For example, the conceptual map shown in Figure 1 .

See Full Size >

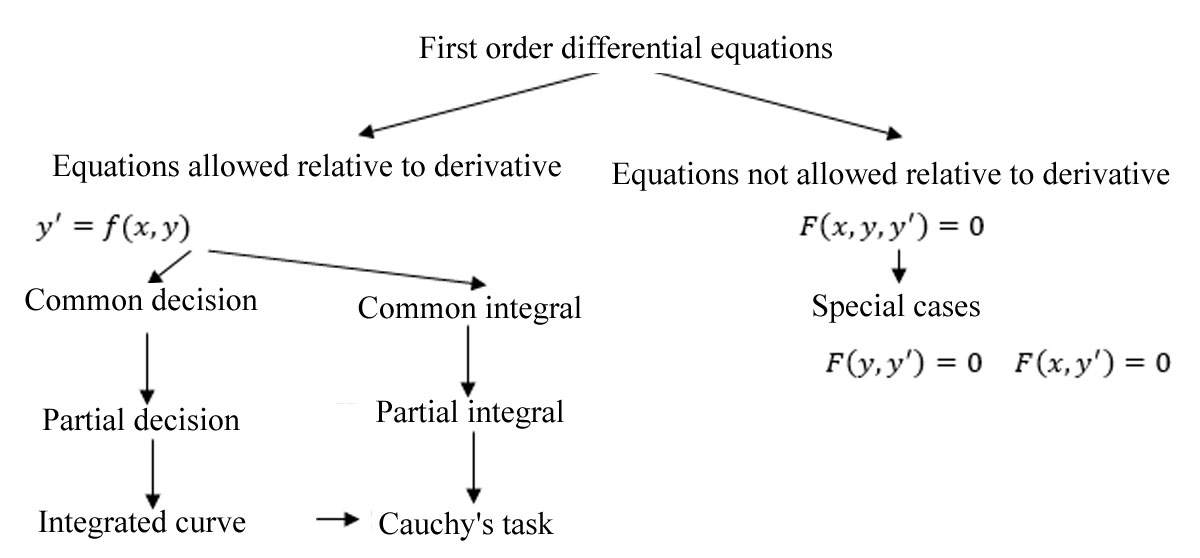
An important aspect in conceptual maps is their hierarchical structure. Conceptual cards should be organized in this way, when the most general and significant concepts appear at the top of the map. As we go down the map, the rank of the concepts presented decreases. Concepts with the same rank should appear on the map at about the same level.

Analysis of the concept map presented in Figure 2 shows that first-order differential equations fall into two main classes: equations resolved with respect to the derivative, i.e., differential equations of the form y '= f (x, y), and equations that are not resolved with respect to the derivative, i.e. differential equations of the form F (x, y, y ') = 0. The study of the first class of equations is quite accessible to high school students and they focus on the system of additional education. As for the second class of equations, they are much more complicated and are studied by students at universities in the course of higher mathematics. For high school students, it’s enough to get acquainted with only a few special cases that are accessible to their understanding.

The study of new concepts in a course of mathematics, as a rule, takes place on the basis of already known concepts, and the solution of new problems often comes down to already solved known problems. Being built into the existing knowledge of schoolchildren, new concepts and facts become their property, firmly and permanently assimilated, easily and quickly updated in case of demand. This helps students to use a workbook designed to play a significant role in organizing students' independent work, both at the stage of assimilation and consolidation of new material, and at the stage of repeating the material passed. The advantage of using a workbook also lies in the fact that it allows a more rational and economical use of study time, since students are freed, in particular, from the need to rewrite the text of tasks and can pay more attention to the implementation of the proposed tasks, and the teacher has the opportunity not only to identify gaps in the knowledge of senior schoolchildren on a particular topic, but also to organize individual work with those who have difficulty in completing assignments on any topic am

In the system of additional education, it is advisable to use excursions to connect the theory with practice, life tasks and laboratory and practical work, under which conditions are created for students to demonstrate independence, acquire practical skills, and, in addition, students are convinced of the many connections of mathematics with other areas of knowledge. We proposed topics of laboratory and practical work and excursions.

Considering all of the above, we offer a model we have developed (Figure 2 ) for studying elements of the theory of differential equations in a supplementary education system using the method of mathematical modeling, the purpose of which is the ability and willingness of high school students to use the material studied and the practical skills and skills acquired in quasi-professional, and then in professional activities.

See Full Size >

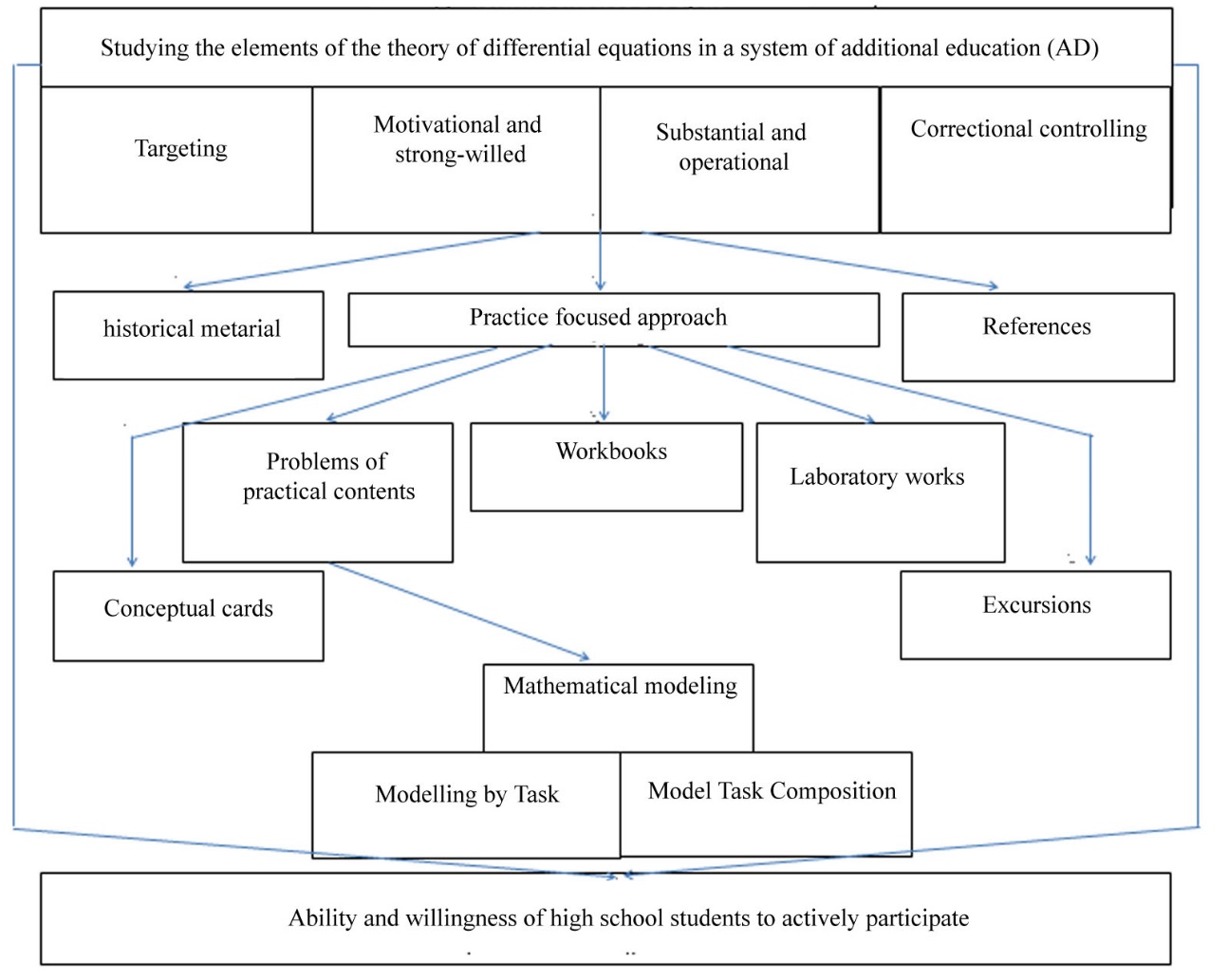
Based on everything we said and the constructed model, we offer the following methodological ways of studying the elements of the theory of differential equations in the system of additional education based on a practice-oriented approach:

• the use of conceptual maps in order to achieve the integrity of the theoretical knowledge of students, their awareness and systematic nature and flowcharts for clarity in knowledge,

• familiarization with the method of mathematical modeling – one of the main in mathematics used in solving professional problems,

• the use of practice-oriented tasks that deepen and expand the knowledge of schoolchildren familiarizing with different types of professional activity,

• the use of workbooks to achieve deep and lasting conscious knowledge of students, the ability to apply the acquired knowledge to solving practical problems,

• conducting laboratory and practical work, allowing communication with other sciences,

• the organization of excursions that implement a connection with life and practice.

Studying a fragment of the theory always involves some propaedeutic work, in this case, students should recall the concepts of derivative, differential, differentiation technique, geometric and mechanical meanings of derivatives, not only using the question-answer form, but also using active methods: solving oral tasks, drawings, etc.

An important role for creating systematic conditions in training, for a deep and clear understanding of specific topics in the theory of differential equations, is played by conceptual maps of the elements of the theory and solutions of these equations.

Conceptual maps are constructions that require students to carefully identify the underlying structure of the material being studied. With their help, one can show how new information is embedded in what is already known when studying the fundamental concepts of the theory of differential equations, such as the equation allowed and not resolved with respect to the derivative, the general solution and the particular solution, the general integral and the partial integral, the integral curve , initial condition, the problem of Cauchy and others.

Prior to the development of conceptual maps, the most used concepts related to the content of the material under study should be selected. Block diagrams (algorithms) are closely connected with concept maps, which in our case provide methods for integrating the main classes of differential equations.

Conceptual maps are compiled throughout the course of studying elements of the theory of differential equations. First, students compose them with the help of a teacher, identify the main stages of compiling conceptual maps. As a result, an algorithm similar to the following is created for creating conceptual maps:

• Select a fragment of the theory for which a conceptual map is compiled,

• To highlight the basic concepts in this fragment,

• To determine the rank of the distinguished concepts by levels depending on the degree of significance, considering the fact that several different concepts can be of the same rank,

• Establish a hierarchy of concepts (indicate more or less significant concepts),

• Place the most significant concepts at the top of the map, place peer concepts at the same level,

• Create a conceptual map for this theoretical fragment.

Students understand what conceptual maps are, what basic elements they include, how the connections between the elements are depicted.

The theoretical knowledge of students is consolidated and deepened by solving plot problems leading to differential equations. Particular attention is paid to practice-oriented tasks, in solving which students form certain forms of thinking necessary to understand the phenomena and processes that occur in the world around us. It is the practice-oriented tasks that show students the importance of the applied nature of mathematics. The task, as you know, is an essential element in the mathematical preparation of students. The practice-oriented tasks, in addition, introduce high school students to the connection between the processes and phenomena of the real world and its mathematical models. With skillful selection of tasks, formalism in the knowledge of students is eliminated and the process of consolidating educational material is activated.

Students want to learn about specific examples of applications of mathematical knowledge related to the phenomena they encounter in everyday life. Therefore, they are offered tasks similar to the ones below.

Task 1. What should be the shape of the satellite dish so that the reflected radio signals are parallel?

Task 2. The cooling rate of water in the kettle is proportional to the temperature difference between the kettle and the kitchen. The kettle turned off at 10.20 at a water temperature of 100 °C. At 10.30 the water temperature in the kettle was 80 °C. Find the time during which the water temperature in the kettle will be 40 °C, if the temperature in the kitchen is 20 °C.

Task 3. The rate of reproduction of bacteria is proportional to their number. At the initial moment t = 0, there were 100 bacteria, and within 3 hours. their number has doubled. Find the dependence of the number of bacteria on time. How many times will the number of bacteria increase within 9 hours?

Task 4. Compression of the coil spring in proportion to the applied force. calculate the work of force when compressing the spring by 0.04 m, if 10 n is needed to compress it by 0.01 m.

Task 5. In the culture of brewer's yeast, the growth rate of the active enzyme is proportional to its present quantity x. The initial amount of the enzyme doubled within 1 hour. How many times will it increase after 3 hours?

Problems of intravenous glucose nutrition, radioactive decay, body cooling, seed germination, watermelon spoilage during transportation, finding the law of bacterial reproduction, cell growth over time, cell destruction in the sound field, the body's response to the introduction medicines, on the functions of supply and demand, etc. illustrate for students numerous situations from different areas of human activity, resolved by the method of compiling a mathematical model in the form of a differential equation, the solution which gives an answer to the question posed by life circumstances. In addition, students see the application of the theory of differential equations in various professions (physicist, physician, agronomist, pharmacist, economist, etc.). Practice-oriented tasks solved using differential equations are also a means of preparing students for the choice of a profession. And the tasks of compiling and solving differential equations in the theory of epidemics show schoolchildren the vitality and importance of the mathematical apparatus in the form of differential equations for such a problem of mankind as the centuries-old struggle against epidemics that have mowed people for centuries.

To solve problems by the method of differential equations with high school students, algorithms for solving these problems are compiled. For example, to solve problems of geometric content, the algorithm may look like this:

• a drawing of the task situation is made,

• the geometric meaning of the derivative is used,

• designations of quantities included in the problem are introduced through x, y and y ',

• a mathematical model is compiled in the form of a differential equation based on the relationship between the values given in the problem,

• the resulting differential equation is solved,

• a conclusion is made.

As an example of the problem solved by this algorithm, we give the following.

Task 6. What should be the shape of the reflective surface so that a parallel beam of light of any width is collected strictly at one point?

In the classroom it is necessary to bring historical and mathematical material. It is advisable to invite students to prepare presentations on the history of the development of the theory of differential equations. Thanks to this, acquaintance with the names, biographies, scientific achievements and life paths of specific historical personalities – scientists and mathematicians. It’s good to attract fiction. So, solving the first of these problems, you should turn to the story of A.N. Tolstoy "Hyperboloid engineer Garin." The connection of mathematics with literature will show students of abstract science mathematics from a different perspective. All this contributes to the interest of students in the study of the proposed material.

The use of a workbook contributes to the activation of mental activity and the independent work of senior schoolchildren in the assimilation of new material both in the classroom and at home. A feature of the workbook is: abstractness, concise presentation, concentration on the principal points of the topic. A workbook can also be fruitfully used by them in preparation for tests.

The workbook helps in solving the problem of increasing the volume of independent mental and practical actions of high school students, creating favorable conditions for the formation of the ability to independently analyze, draw conclusions, substantiate their practical actions.

The following structure of the workbook on the topics of the theory of differential equations in the framework of the system of additional education is proposed: – definition of the basic concepts of the topic; – the connection of new concepts with previously studied concepts; – a dictionary of new concepts; – the purpose and main tasks of this topic; – an algorithm for solving tasks on this topic; – creative exercises; – questions for self-control (to answer them, students can work with notebooks, textbooks and teaching aids); – fulfillment of key tasks of the topic according to the proposed algorithm; – tasks for independent work of varying difficulty; – test; – testing; – use of information and communication technologies.

One of the forms of teaching the elements of the theory of differential equations that contributes to the development of skills necessary for practical activities is laboratory and practical work. They allow students to more fully and consciously understand the relationships between values; to establish closer links between various topics of the theory of differential equations and topics of school mathematics.

Conducting laboratory and practical work with high school students introduces a variety of math classes; increases the activity and independence of high school students in the lesson; contribute to raising the level of knowledge of high school students in mathematics; makes abstract theoretical propositions understandable, accessible, visual.

Laboratory-practical work includes students' independent work carried out through observations, comparisons, measuring and computing tools, compiling tables, plotting graphs, studying mathematical formulas, drawings, figures, in order to establish new mathematical facts for students, which are the basis for theoretical conclusions and generalizations, and, subsequently, receiving, if necessary, rigorous logical proof".

When mastering the elements of the theory of differential equations, field trips are provided. It is obvious that it is impossible to give students a complete picture of modern production, for which they are prepared to work, without visiting it. Many issues can be addressed in a clear, understandable way for students only by directly familiarizing themselves with certain subjects in their natural environment. Therefore, excursions are a fairly effective way of introducing students to modern technology, technology and the organization of production directly in the enterprise. Thus, excursions are one of the types of organized observations of production processes or objects under the guidance of a master on a farm, in an individual farm, at a construction site, etc., i.e., in real production conditions. Most often, excursions are conducted in order to collect data for the compilation of the task, the source for the plot and numerical data of which is the excursion object.

The construction of excursions and the sequence of their conduct vary depending on the purpose, the season. Bringing high school students to the place of excursion, the teacher in a brief conversation recalls the purpose of the lesson, gives them a look around, then high school students begin to observe the intended objects. The main part of the tour is a collective observation. Here the main program tasks of the lesson are solved. The teacher of continuing education helps older students to notice and understand the characteristic signs of objects and phenomena. He supplements the observations with his story and explanation. The main attention in the observation is paid to questions, questions, tasks, forcing students to consider the subject, compare, find the difference and similarity, establish a connection between natural phenomena. At the end of the main part, it is necessary to give children the opportunity to satisfy curiosity in individual independent observations and collecting material. However, giving the task to collect material, one should strictly limit its quantity in order to focus the attention of older adolescents only on the necessary.

For example, an excursion to a bakery of a private producer brought senior students to the task with the following plot basis.

Task. Within 20 minutes, the temperature of the bread removed from the oven and placed in the warehouse drops from 1000 to 600. The air temperature in the warehouse is 180. After how much time from the moment of cooling the temperature of the bread drops to: 1) 360? 2) 250?

It has been experimentally shown that the introduction of the developed methodology of studying the elements of the theory of differential equations in high school students on the basis of a practice-oriented approach using the method of mathematical modeling in the system of additional education increases the success of mastering the proposed material.

At the beginning and at the end of the experiment, senior pupils were questioned in the control and experimental groups in order to find out the subjective opinions of students about the problem and independent work for an objective analysis of the levels of success in the assimilation of the proposed material by schoolchildren before and after the experiment.

The questionnaire contained 5 questions:

• Are you familiar with the concept of a differential equation?

• On what knowledge is the solution of differential equations based?

• Do you know how to solve differential equations?

• Are differential equations applied in practice, in life?

• Do you want to learn how to solve differential equations?

The questionnaires before and after the experiment had the same questions, but the answers of the students to them were very different in the experimental group compared to the control group. In the control group, the answers of schoolchildren before and after the experiment were practically the same, since classes in it were conducted according to the established traditional methodology. In the experimental group, the number of students who answered 3, 4, 5 questions positively increased significantly.

The goal of the ascertaining stage was to study the state of the problem of studying the elements of the theory of differential equations in the system of additional education based on a practice-oriented approach. To do this, we studied school documentation, attending classes, conversations with teachers, students, student surveys. As a result, it was possible to draw the following conclusion: education in high school touches on elements of the theory of differential equations, they are rarely studied in the system of additional education – in high school there is no time for this, and there and there there is no methodological support for studying this material.

Based on the conclusions of the ascertaining stage of the experiment and theoretical analysis of the problem, the formative stage of the experiment was carried out in accordance with the proposed model. It was attended by 186 students, with 92 students falling into control groups, and 94 – in the experimental group. The study of the elements of the theory of differential equations took place according to the method developed by us, and in control classes according to the traditional method.

The effectiveness of the results was checked at the control-ascertaining stage of the experiment. The effectiveness of the developed methodology was judged by the following criteria: – the ability to compose a conceptual map of a fragment of the theory of differential equations, – the ability to draw up a model of a practice-oriented problem (in the form of a differential equation), – the ability to solve the resulting differential equation, – the ability to correctly interpret the result in terms of this tasks, – the ability to compose a plot practice-oriented task (according to this model), – the ability to correctly perform laboratory and practical work, – the ability to avit task according to the production tours and solve it by the method of mathematical modeling by differential equations, – the ability to draw conclusions. Three levels are distinguished: high – 7–8 skills, medium – 4-6 skills, low – 2-3 skills.

The diagrams below show the generalized results of measuring the success levels of high school students in mastering the elements of the theory of differential equations before and after the experiment. The data were obtained as a result of independent work in both groups: one after the experiment, the other after. Both contained 5 tasks, each of which allowed to reveal the presence of certain skills in students. The text of the first independent work consisted of the simplest differential equations and practice-oriented problems, the solution of which was reduced to the simplest differential equations. An analysis of the work showed that not all students coped with the tasks. We give the text of the second independent work.

Independent work number 2

1. Create a conceptual map for differential equations with separable variables.

2. It is known that the multiplication rate of some bacteria is proportional to the number of bacteria at a given moment with a proportionality coefficient k. Determine k if there were 2,000 bacteria in the vessel at 10 o’clock, and 32,000 at 12 o’clock.

3. To compose a task according to the differential equation:

$$\frac{dx}{dt}kx,$$

4. Based on the data obtained during an excursion to the economy of an individual entrepreneur, compose a problem to be solved using the differential equation.

5. Experimentally obtain the dependence of shortening (stretching) of the arm muscles when lifting weights.

See Full Size >

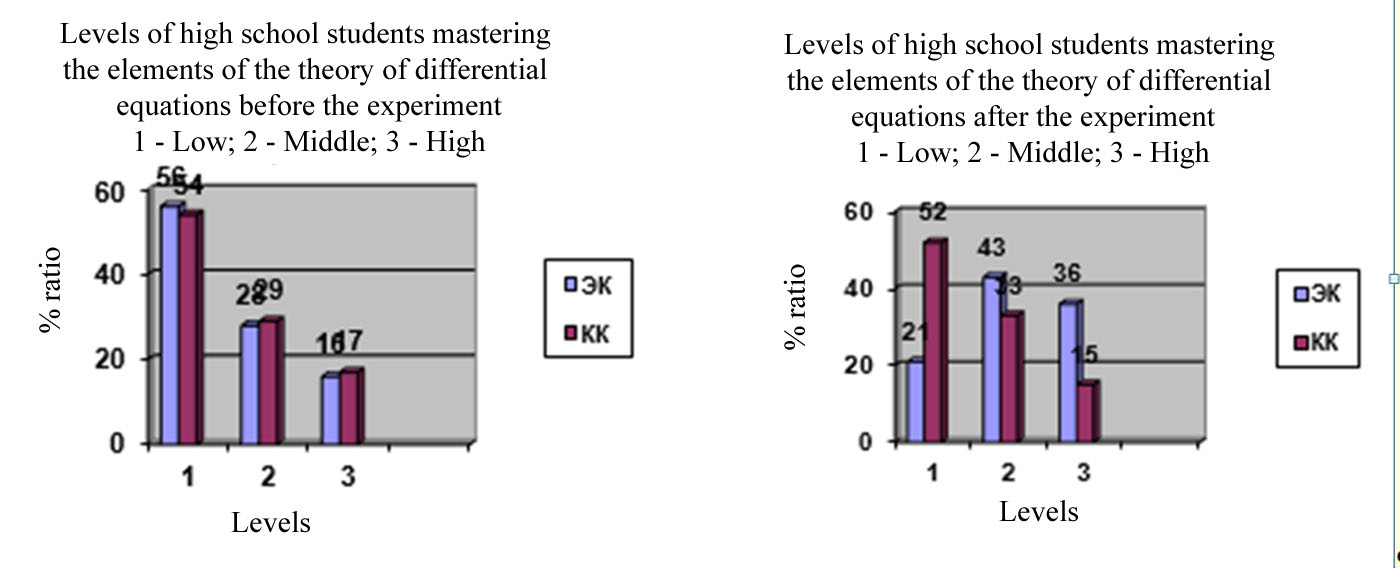
The diagrams (Figure 3 ) show that during the experiment the number of high school students of middle and high levels of the experimental group significantly exceeds the same indicator for the control group, the changes in which are insignificant. The statistical significance of the differences was verified using the $X^{\mathrm{2}}$ – square test. The data obtained statistically processed using the $X^{\mathrm{2}}$ – squared criterion data allow us to conclude that the method proposed by the author helps to increase the level of mastery of the elements of the theory of differential equations by high school students, and therefore the ability and readiness for its active use in future professional activities.

Conclusion

A methodology has been developed for studying elements of the theory of differential equations in a system of additional education based on a practice-oriented approach using the method of mathematical modeling. Thereby, a certain contribution was made to:

• development of the provisions of a practice-oriented approach applied to the study of elements of the theory of differential equations of the first order in the framework of additional education,

• the methodology of using the method of mathematical modeling in the system of additional education in solving differential equations of the first order,

• the content of additional education through the justification and developed methodology for studying the elements of the theory of differential equations of the first order,

• the process of compiling practice-oriented tasks solved by the method of mathematical modeling, moreover, differential equations of the first order are used as a model.

The theoretical significance of the study lies in the fact that – is presented (in the form of a model) a technique for studying by high school students in the framework of additional education of elements of the theory of differential equations;

The practical significance of the work lies in the fact that the developed methodology for studying the elements of the theory of differential equations based on a practice-oriented approach for high school students can be implemented not only in the system of additional education, but also be used in the educational process of educational institutions and in the framework of pre-university training.

Solving a wide class of practice-oriented problems with students devoted to resolving situations from different fields of knowledge and human activity, we thereby affirm them in the thought that such diverse problems are solved by the same mathematical model – the differential equation. At the same time, students establish interdisciplinary connections, more firmly grasp the essence and stages of the method of mathematical modeling, acquire solid skills in creating models and solving differential equations, get acquainted with numerous phenomena and processes that allow them to get an idea of ​​some professions, and also learn more fully from related disciplines .

The article is useful to teachers of additional education and faculties of pre-university training, teachers of mathematics schools of different levels and profiles.

References

• Ammosova, N. V. (2005). Some aspects of the preparation of mathematics teachers for work in the system of additional education for schoolchildren. Sci. of the Kuban, 2, 174–179.
• Ammosova, N. V., & Krasnova, G. G. (2012). Implementation of continuity in teaching mathematics in primary and high school (by the example of the study of equations). Siber. Pedag. J., 3, 252–256. Retrieved from http://sp-journal.ru/journal/2012-3
• Anosov, D. V. (2001). Mathematics at glance and something from it. Moscow. Mysl.
• Aslanov, P. M. (1997). Methodical system of teaching differential equations in a pedagogical university (Doct. Dissertation thesis). Moscow. Retrieved from http://www.dissercat.com/content/metodicheskaya-sistema-obucheniya-differentsialnym-uravneniyam-v-pedvuze (accessed 7 March 2017).
• Bavrin, G. I. (1998). Strengthening the professional and applied orientation of teaching mathematical analysis at a teacher training university: On the material of the course “Differential Equations” (Cand. dissertation). Moscow.
• Dalinger, V. A., & Simonzhenkov, S. D. (2008). Modeling using differential equations. Textbook. allowance. Omsk: LLC CPI “Sphere”.
• Gerbekov, H. A. (1991). Differential equations in the vocational training system of a mathematics teacher in a teacher training university. (Cand. dissertation). Moscow.
• Lvov, V. D. (2009). Professional orientation of teaching mathematics to students of chemical and technological specialties of technical universities (on the example of the section “Differential Equations”) (Cand. Dissertation thesis). Astrakhan.
• Melnikov, P. M. (2007). Integration of fundamental and applied components in teaching differential equations to future physics teachers (Cand. Dissertation). Dace.
• Naimanov, B. A. (1992). Implementation of the applied orientation of teaching differential equations in a pedagogical institute (Cand. Dissertation). Moscow.
• Plotnikova, C. B. (2000). Professional orientation of teaching mathematical disciplines to students of technical universities (Cand. Dissertation). Samara
• Polekhina, G. E. (1996). Differential equations as the final stage in the development of the methodological line of equations in school (Cand. Dissertation thesis). Moscow.
• Rodionov, M., & Dedovets, Z. (2018). Developing students' motivation for learning through practical problems in school. Advances in Science, Technology and Engineering Systems, 3, 258–266.
• Rodionov, M., & Velmisova, S. (2008). Construction of Mathematical Problems by Students Themselves. Proceedings of the 34th Conference on Applications of Mathematics in Engineering and Economics (AMEE '08) (pp. 211–228). (Sozopol, Bulgaria, 8–14 June 2008). Publ. December 2008.
• Rodionov, M. A., Akimova, I. V., & Shabanov, G. I. (2017). Elements of “fuzzy logic” as a component of professional and pedagogical training of future mathematics and informatics teachers. Integration of Education, 2, 286–299.
• Rodionov, M. A., Fedoseyev, V. M., Dedovets, Z., Shabanov, G. I., & Akimova, I. V. (2018). Specifics of designing a technological component in an integrated methodological system of mathematical training of future engineers. Integration of Education, 2, 383–400.
• Ryzhakov, M. V. (1999). Theoretical foundations of the development of the state standard of general secondary education (Doct. Dissertation thesis). Moscow.
• Sycheva, N. V. (2013). Methodology for the study of differential equations by means of search activity by students of technical areas of training (Cand. Dissertation). Bryansk.