Geographically Weighted Regression Model: A Potential Approach For Better Management Of Urban Growth

Abstract

Many urban areas are experiencing high impact of urbanization pressures and loss of potential biodiversity due to rapid pace of urban development and economic restructuring. The urban areas are expanding at an alarming rate and their frequency, intensity and distribution of growth vary spatially. Given the dynamic nature of urban development and environmental conditions, it is imperative to understand urban growth in order to strategize and regulate urban land use more efficiently. In this context, spatially explicit models are helpful to land use planners and managers because these models consider the arrangement of urban development and its relationship with urban variables over space and time. It provides more insight on patterns and processes thus provide information on future developments to support decision making. This paper discusses the potentials of Geographically Weighted Regression (GWR) model as a spatial modelling for better understanding and as management strategies of urban growth. GWR has gaining increasing interest in many urban studies to address diverse urban issues. Parameter values in GWR are distributed according to proximity to the observation and those parameter values are assigned higher weights to nearby observations. GWR provides a framework for evaluating how the strengths of relationships change with the spatial resolution of the analysis. In Malaysia, GWR may have potential in better managing urban growth and predicting urban growth patterns.

Keywords: Geographically Weighted Regressionspatial modellingnon-stationarityurban growth managementMalaysiat

Introduction

Malaysia is experiencing rapid urbanization resulting from population increase and in-migration to urban areas ( Abdullah, 2003). Recent projections indicated that the urbanization process in Malaysia would result in urban population exceeding 65 percent by the year 2020 ( Government of Malaysia, 2010). This trend results in urban areas expanded to fulfil the increasing demands of the population. The dynamic growth of the urban population will call for adequate housing and infrastructures ( Osman, Nawawi, & Abdullah, 2008). To model current and future urban development, the driving factors of urban growth need to be recognized. Over the years, some areas of small isolated human settlements in Malaysia have been transformed into interconnected metropolitan regions. Sprawl is the relocation of development to urban peripheral areas due to the change in lifestyles and preferences ( Osman et al., 2008). This influx into the city’s periphery areas has increased the housing, transportation and other infrastructure needs, thus acknowledged as a phenomenon of global importance and serious threat to urban ecosystems ( Mundia & Aniya, 2006; Jat, Garg, & Khare, 2008).

Rapid urban growth is the characteristics of developing countries ( Dewan & Yamaguchi, 2009; Thapa & Murayama, 2010; Patra, Sahoo, Mishra, & Mahapatra, 2018). To relate the spatial pattern of rapid urbanization and its driving forces, explicit spatial models and analysis methods are needed. Modelling and simulation of diverse urban growth scenarios has become paramount progress in land use and sustainable urban development researches. The processes of land use change in quantitative terms and for testing our understanding of the processes can be described by spatial models ( Serneels & Lambin, 2001). The growing issues of spatial non-stationarity in many traditional urban models have prompted urban researchers to develop various local regression techniques. Among them is the geographically weighted regression (GWR) technique which is used to identify the potential non-stationarity in the relationship between the dependent and independent variables ( Fotheringham, Brunsdon, & Charlton, 2002). A group of local parameter coefficients are estimated for each observation points and GWR lets the model parameters to vary in space (Fotheringham et al., 2002, Fotheringham, Charlton, & Brunsdon, 2001). The technique assigns higher weight to the observations spatially closer to the location being predicted than those farther away. While traditional regression models estimate only one global parameter estimate for all observations, GWR generates spatial data that expresses the spatial distribution in the relationships between variables and uses maps to generate and interprete spatial non-stationarity ( Mennis, 2006). Like other nations, Malaysia is also striving to achieve a sustainable urban growth and natural resources management. In this article, we discuss the potentials of GWR as a spatial regression modelling tool in urban growth management in Malaysia.

Problem Statement

Numerous applications have proven the usefulness of GWR as a local model for spatial relationship ( Brunsdon, McClatchey, & Unwin, 2001; Fotheringham et al., 2001; Huang & Leung, 2002; Malczewski, Poetz, & Iannuzzi, 2004; Lloyd & Shuttleworth, 2005; Yu, 2006; Lochl & Axhausen, 2010; Chen, Han, & de Vries, 2020). GWR has become a more commonly used technique in urban studies by addressing diverse urban problems. GWR applications have widespread in the fields of ecology ( Zhang & Shi, 2004; Kimsey, Moore, & McDaniel, 2008), climatology ( Brunsdon et al., 2001), education ( Fotheringham et al., 2001), marketing research ( Mittal, Kamakura, & Govind, 2004), regional science ( Huang & Leung, 2002), political science ( Calvo & Escolar, 2003), and transport research ( Nakaya, 2001; Lloyd & Shuttleworth, 2005; Zhao, Chow, Li, & Liu, 2005; Chow, Zhao, Liu, Li, & Ubaka, 2006; Du & Mulley, 2006; Clark, 2007). Moreover, GWR has been applied to examine regional variations in the link between environmental variables and socio-economic indicators and to investigate geographic heterogeneity in urban and regional growths ( Yu, 2006; Partridge, Rickman, Ali, & Olfert, 2008). Páez, Uchida, and Miyamoto ( 1999) used GWR to determine the spatial variation of spillovers in land markets, whereas McMillen ( 2001) identified urban sub-centers using the local regression model. Laffan ( 1999) used it to assess spatial model errors, while other substantive applications include a study on regional industrialization in China by Huang and Leung ( 2002). Li, Corcoran, Pullar, Robson, and Stimson ( 2009) developed GWR models to compute forecasts of regional employment for South East Queensland in Australia. Helbich and Leitner ( 2009) examined the driving factors of urban-to-rural migration in the Austrian metropolitan area of Vienna and used GWR approach to determine whether the suburban or post-suburban determinants are essential to predict urban-to-rural migration. Those studies indicated that the GWR models have better predictive power and provides an improved understanding of the spatial variations.

In Malaysia, studies on the issues of urban growth and land use, sustainable urban development, urban planning and conservation had long used traditional regression approach ( e.g. Abdullah, 2003; Jaafar, 2004; Rainis & Noresah, 2004; Tahir & Roe, 2006; Samat, 2007; Lee, Lim, & Nor’Aini, 2008; Osman et al., 2008; Tan, Lim, MatJafri, & Abdullah 2009). On the other hand, studies which used GWR include modelling urban spatial structure Noresah and Rainis, (2009), analyzing land use change ( Noresah, Gairola, & Talib, 2010), assessing the rental value of shop houses ( Eboy, Ibrahim, & Buang, 2006) and examining the locational attributes effect on residential property values ( Dziauddin & Idris, 2017). This indicates that studies on understanding the spatially varying relationship between urban growth patterns and determinants using the GWR approach in the Malaysian context are yet to be explored.

Research Questions

• What is the application of Geographically Weighted Regression in urban studies?

• What is the potential use of Geographically Weighted Regression model as a spatial regression modelling in urban growth management?

Purpose of the Study

Generally, there are two properties of spatial data which are spatial autocorrelation and non-stationarity. Geographically weighted regression (GWR) has become popular when non-stationarity issue is suspected. GWR was proposed by Brunsdon, Fotheringham, and Charlton ( 1996) as a method to examine spatially varying relationships ( Fotheringham et al., 2002). In an ordinary regression (for e.g. OLS) it is assumed that the regression parameters are "whole-map" statistics. However, in many cases, the residuals (the difference between the observed and predicted data) may reveal the variation and can be visualized by mapping. Many different solutions have been proposed for dealing with spatial variation in the relationship, but GWR provides an elegant and easily grasped means of modelling such relationships. GWR model captures spatial variations in the regression parameters that change over the geographical space. Thus, the purpose of this study is to analyze the use of GWR in urban growth management to understand the spatially varying relationship between urban growth patterns and the determinant factors.

Research Methods

Geographically Weighted Regression model analyzes spatially varying relationship between dependent variable and the explanatory variables. GWR weighted data samples based on their spatial proximity and every observations across the study area have different regression parameters ( Li et al., 2009). The weighting of all neighbouring observations utilized the distance decay function to obtain the local estimation of model parameters as observations nearer to the location of the sample point have more influence on the regression point than the observations farther away. GWR generates parameter estimates for every regression point in a given neighbourhood thus allows for the measurement and mapping of local as opposed to global models of relationships. The parameters can be mapped (using GIS) to represent non-stationarity over the study space. Similarly, local measures of standard errors and goodness-of-fit statistics can be obtained ( Fotheringham, Brunsdon, & Charlton 2000). Therefore, the additional feature of GWR is that it offers the potential of increased understanding on the nature of varying relationships between variables across space ( Cheng, Masser, & Ottens, 2001). Mennis ( 2006) and Gao and Li (2011) also provided a brief, comprehensive overview and theoretical background of GWR model.

The traditional global regression model can be expressed as:

y ^ i = β 0 + ∑ k β k x i k + ε i

where y ^ i is the estimated value of the dependent variable at location i , β 0 represents the intercept, β k expresses the slope coefficient for independent variable x k , x i k is the value of the variable x k at location i , and ε i denotes the random error term for location i . In this equation, the estimates of the model parameters are assumed to be spatially stationary. But in reality, there will be intrinsic differences in relationships over space which may imply non-stationary character. This non-stationarity problem can be measured using GWR ( Fotheringham et al., 2002; Platt, 2004). Conceptually, the GWR extends conventional global regression by generating a local regression equation for each observation. Each equation is calibrated using a different weighting of the observations contained in the data set.

The GWR equation can be written as:

y ^ i = β 0 µ i , v i + ∑ k β k µ i , v i x i k + ε i

where ( µ i , v i ) denotes the coordinate location of the i th point ( Fotheringham et al., 2002 ), β 0 µ i , v i is the intercept for location i , β k µ i , v i represents the local parameter estimate for independent variable x k at location i . Parameter estimates in GWR are obtained by weighting all observations around a specific point i based on their spatial proximity to it. The observations closer to point i have higher impacts on the local parameter estimates for the location and are weighted more than observations farther away. The parameters are estimated from:

β ^ µ , v = ( X T W µ , v X ) - 1 X T W µ , v Y ,

where β ^ µ , v represents the unbiased estimate of β , W µ , v is the weighting matrix which functions to ensure that observations near to the specific point have bigger weight value. The weighting function (i.e. kernel function) can be stated using the exponential distance decay form:

W i j = e x p d i j 2 b 2

where W i j represents the weight of observation j for location i , d i j expresses the Euclidean distance between points i and j , and b is the kernel bandwidth. If observation j coincides with i , the weight value is one. If the distance is greater than the kernel bandwidth, the weight will be set as zero ( Fotheringham et al., 2002 ).

The spatial kernel can take either a fixed (distance) or adaptive (number of samples) to establishing the radius of the local GWR model ( Fotheringham et al., 2002). Figure 1 show fixed spatial kernel and adaptive spatial kernel. Windle, Rose, Devillers, and Fortin (2009) cautioned on the selection of the size of the kernel bandwidth as it has a significant impact on the outcome of the GWR analysis.

See Full Size >

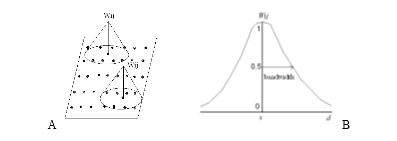
Cross-validation score using algorithm as stated below can be optimized to set the bandwidth.

C V = ∑ i = 1 n ( y i - y ^ i ≠ i ) 2

where n is the number of observations, and observation i is omitted from the calculation so that in areas of sparse observations the model is not calibrated solely on i . Alternatively, the bandwidth may be chosen using the Akaike Information Criteria (AIC) score ( Mennis, 2006). More details on the theory and practical application of GWR technique can be found in the literature ( Brunsdon, Fotheringham, & Charlton, 1998; Fotheringham et al., 2002).

In addition, spatial relationships depend greatly on scale, which exist in natural and man-made patterns and processes ( Lü and Fu, 2001). Gao and Li, (2011) suggested changing the bandwidth of GWR to estimate local parameters and to detect spatial non-stationarity at multi scales analysis. The book ‘Geographically Weighted Regression: the analysis of spatially varying relationships’ authored by Fotheringham et al. ( 2002) is recommended for anyone who are interested in applying GWR in their research.

Findings

Studies on urban growth using GWR had shown an increased in the strength of association between urban builtup area and factors associated with urban growth change mainly in terms of the goodness-of-fit statistics (R ²) ( Noresah & Rainis, 2009; Noresah et al., 2010), the slopes of the parameter to be general over the observed area. When the global (OLS) model and the local (GWR) model were compared the studies found that R ² for OLS global model was lower than for GWR model, with individual regression coefficient for GWR model ranging from 0.0 to 0.99. The regression parameters for GWR varied accross the study area. While Noresah et al. ( 2010) reported the spatial variation of the regression parameter over the space when mapped using Geographic Information System. GWR method has the advantage of revealing interesting pattern of spatial variation or nonstationarity of parameters which is useful for urban growth management strategy.

Conclusion

With the new paradigms on sustainable development, the study of urban structure changes is becoming one of the important global challenges. Urban researchers have recognized GWR as a spatial regression modelling approach capable to develop more comprehensive understanding about complex urban systems and thus improve strategies for urban growth management. Nevertheless, there are some limitations to the method and that the findings from GWR should be interpreted with caution ( Cheng et al., 2001; Shearmur, Apparicio, Lizion, & Polèse, 2007). Hence, GWR is valued more in providing the urban modeller with an alternative approach to data management, spatial analysis and visualization. In the context of Malaysia, some researchers used GWR approach to comprehend the relationships between urbanization and its influencing factors, in modelling urban spatial structure and transportation and in market research etc. However, substantial effort is still needed for better understanding of urbanization patterns, spatial structure of rapidly growing cities, sustainable transportation as well as urban environmental modelling. This clearly indicates that GWR can also be used in ecological and environmental studies to better understand the patterns and in planning the strategies for conservation of the unique urban biodiversity and landscape of Malaysia.

References

• Abdullah, J. (2003). The suburbanization of the Kuala Lumpur Metropolitan Region. Journal of the Malaysian Institute of Planners, 1, 119-126.
• Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geographical Analysis, 28, 281-298.
• Brunsdon, C., Fotheringham, S., & Charlton, M. (1998). Geographically weighted regression- modeling spatial non-stationarity. The Statistician, 47, 431-443.
• Brunsdon, C., McClatchey, J., & Unwin, D. (2001). Spatial variations in the average rainfall-altitude relationship in Great Britain: an approach using geographically weighted regression. International Journal of Climatology, 21, 455-466.
• Calvo, E., & Escolar, M. (2003). The local voter: A geographically weighted approach to ecological inference. American Journal of Political Science, 47(1), 189-204.
• Chen, H. C., Han, Q., & de Vries, B. (2020) Urban morphology indicator analyzes for urban energy modelling, Sustainable Cities and Society, 52, Article Number 101863.
• Cheng, J., Masser, I., & Ottens, H. (2001). Understanding urban growth system: theories and methods. Department of urban and regional planning, ITC institute, Netherlands.
• Chow, L. F., Zhao, F., Liu, X., Li, M. T., & Ubaka, I. (2006). Transit ridership model based on geographically weighted regression. Transportation Research Record, 1972(1), 105-114.
• Clark, S. D. (2007). Estimating local car ownership models. Journal of Transport Geography, 15(3), 184-197.
• Dewan, A. M., & Yamaguchi, Y. (2009). Land use and land cover change in greater Dhaka, Bangladesh: using remote sensing to promote sustainable urbanization. Applied Geography, 29, 390-401.
• Du, H., & Mulley, C. (2006). Relationship between transport accessibility and land value: Local model approach with geographically weighted regression. Transportation Research Record, 1977(1), 197-205.
• Dziauddin, M. F., & Idris, Z. (2017) Use of Geographically Weighted Regression (GWR) Method to estimate the effects of location attributes on residential property values. Indonesian Journal of Geography, 49(1), 97-110.
• Eboy, O. V., Ibrahim, S., & Buang, A. (2006). Determining location influence for shop house rental value using Geographical Weighted Regression (GWR). Malaysian Journal of Real Estate, 1(2), 1-6.
• Foody, G. (2004) GIS: stressing the geographical. Progress in Physical Geography, 28(1), 152-158.
• Foody, G. M. (2003), Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sensing of Environment, 88(3), 283-293.
• Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2000). Quantitative geography: Perspectives on spatial data analysis. London: Thousand Oaks, California: Sage Publications.
• Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2002). Geographically weighted regression: The analysis of spatially varying relationships. Chichester: Wiley.
• Fotheringham, A. S., Charlton, M., & Brunsdon, C. (1997). Measuring spatial variations in relationships with geographically weighted regression. In M.M. Fischer and A. Getis (Eds.), Recent Developments in Spatial Analysis, Spatial Statistics, Behavioral Modeling and Neurocomputing. London: Springer-Verlag.
• Fotheringham, A. S., Charlton, M., & Brunsdon, C. (2001). Spatial variations in school performance: a local analysis using geographically weighted regression. Geographical and Environmental Modelling, 5, 43-66.
• Government of Malaysia (2010). Tenth Malaysia Plan 2011-2015. The Economic Planning Unit, Prime Minister’s Department. Putrajaya.
• Grimm, N. B., Grove, J. M., Pickett, S. T. A., & Redman, C. L. (2000). Integrated approaches to long-term studies of urban ecological systems. Bioscience, 50, 571-584.
• Helbich, M., & Leitner, M. (2009). Spatial Analysis of the Urban-to-Rural Migration Determinants in the Viennese Metropolitan Area. A Transition from Suburbia to Postsuburbia? Applied Spatial Analysis and Policy, 2, 237-260.
• Huang, Y., & Leung, Y. (2002). Analysing regional industrialisation in Jiangsu province using geographically weighted regression. Journal of Geographical Systems, 4(2), 233-249.
• Jaafar, J. (2004). Emerging Trends of Urbanisation in Malaysia. Journal of the Department of Statistics Malaysia, 1, 43-54.
• Jat, M. K., Garg, P. K., & Khare, D. (2008). Monitoring and modeling of urban sprawl using remote sensing and GIS techniques. International Journal of Applied Earth Observation and Geoinformation, 10(1), 26-43.
• Jenkins, G., & King, V.T. (2003). Heritage and development in a Malaysian city: George Town under threat? Indonesia and Malay World, 31(89), 44-57.
• Kimsey, M. J., Moore, J., & McDaniel, P. (2008). A geographically weighted regression analysis of Douglas-􀄑r site index in north central Idaho. Forest Science, 54(3), 356-366.
• Laffan, S. W. (1999). Spatially assessing model error using geographically weighted regression. In Fourth International Conference on Geo Computation. Mary Washington College, Virginia, USA.
• Lee, M. L., Lim, M. Y., & Nor’Aini, Y. (2008). Strategies for urban conservation: a case example of George Town, Penang. Habitat International, 32, 293-304.
• Li, T., Corcoran, J., Pullar, D., Robson, A., & Stimson, R. (2009). A Geographically Weighted Regression Method to Spatially Disaggregate Regional Employment Forecasts for South East Queensland. Applied Spatial Analysis, 2, 147-175.
• Lloyd, C., & Shuttleworth, I. (2005). Analyzing commuting using local regression techniques: Scale, sensitivity, and geographical patterning. Environment and Planning A, 37(1), 81-103.
• Löchl, M., & Axhausen, K. W. (2010). Modeling hedonic residential rents for land use and transport simulation while considering spatial effects. The Journal of Transport and Land Use, 3(2), 39-63.
• Lü, Y. H., & Fu, B. J. (2001). Ecological scale and scaling. Acta Ecologica Sinica, 21(12), 2096-2105 (in Chinese).
• Malczewski, J., Poetz, A., & Iannuzzi, L. (2004). Spatial analysis of residential burglaries in London, Ontario. The Great Lakes Geographer, 11, 15-27.
• McMillen, D. P. (2001). Nonparametric Employment Subcenter Identification. Journal of Urban Economics, 50, 448-473.
• Mennis, J. (2006). Mapping the results of geographically weighted regression. The Cartographic Regression Journal, 43(2), 171-179.
• Mittal, V., Kamakura, W. A., & Govind, R. (2004). Geographic patterns in customer service and satisfaction: An empirical investigation. Journal of Marketing, 68(3), 48-62.
• Mundia, C. N., & Aniya, M. (2006). Dynamics of land use/ cover changes and degradation of Nairobi City, Kenya. Land Degradation and Development, 17(1), 97-108.
• Nakaya, T. (2001). Local spatial interaction modelling based on the geographically weighted regression approach. GeoJournal, 53(4), 347-358.
• Noresah, M. S., & Ruslan, R. (2009). Modelling urban spatial structure using geographically weighted regression. In Anderssen, R. S., R. D. Braddock & L. T. H. Newham (Eds.), 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation (pp. 1950-1956). Cairns Australia.
• Noresah, M. S., Gairola, S., & Talib, A. (2010). Modelling Urban Land Use Change Using Geographically Weighted Regression and the Implications for Sustainable Spatial Planning. In D.A. Swayne, W. Yang, A.A. Voinov, A. Rizzoli and T. Filatova (Eds.), 5th International Congress on Environmental Modelling and Software’ (iEMSs 2010). Ottawa, Canada.
• Osman, S. B., Nawawi, A. H., & Abdullah, J. (2008). Urban sprawl and its financial cost: a conceptual framework. Asian Social Science Journal, 4(10), 39-50.
• Páez, A., Uchida, T., & Miyamoto, K. (2002a). A general framework for estimation and inference of geographically weighted regression models: 1. Location-specific kernel bandwidths and a test for locational heterogeneity. Environment and Planning, A34, 733-754.
• Paez, A., Uchida, T., & Miyamoto, K. (2002b). A general framework for estimation and inference of geographically weighted regression models: 2. Spatial association and model specification tests. Environment and Planning, A34, 883-904.
• Páez, A., Uchida, T., & Miyamoto, K. (1999). A Spatial Analysis of External Economies and its Association with Transportation Infrastructure: the Case of Sendai City. Journal of the Eastern Asia Society for Transportation Studies, 3(4), 149-164.
• Partridge, M. D., Rickman, D. S., Ali, K., & Olfert, M. R. (2008). The geographic diversity of U.S. nonmetropolitan growth dynamics: A geographically weighted regression approach. Land Economics, 84, 241-266.
• Patra, S., Sahoo, S., Mishra, P., & Mahapatra, S. C. (2018) Impacts of urbanization on land use/ land cover changes and its probable implications on local climate and groundwater level. Journal of Urban Management, 7, 70-84.
• Platt, R. V. (2004). Global and local analysis of fragmentation in a mountain region of Colorado. Agriculture Ecosystems & Environment, 101(2-3), 207-218.
• Propastin, P., Martin, K., & Stefan, E. (2008). Application of Geographically Weighted Regression to Investigate the Impact of Scale on Prediction Uncertainty by Modelling Relationship between Vegetation and Climate. International Journal of Spatial Data Infrastructures Research, 3, 73-94.
• Ruslan, R., & Noresah, M. S. (2004). Modelling urban land use dynamics using GIS and Markov Chain Model. Geoinformation Science Journal, 4(1), 72-81.
• Samat, N. (2007). Integrating GIS and cellular automata spatial model in evaluating urban growth: prospective and challenges. Jurnal Alam Bina Jilid, 9(1), 79-93.
• Serneels, S., Said, M. Y., & Lambin, E. F. (2001). Land cover changes around a major East African wildlife reserve: the Mara Ecosystem (Kenya). International Journal of Remote Sensing, 22(17), 3397-3420.
• Shearmur, R., Apparicio, P., Lizion, P., & Polèse, M. (2007). Space, time, and local employment growth: An application of spatial regression analysis. Growth and Change, 38(4), 696-722.
• Tahir, O. M., & Roe, M. H. (2006). Sustainable urban landscapes: making the case for the development of an improved management system. International Journal on Sustainable Tropical Design Research and Practice, 1(1), 17-24.
• Tan, K. C., Lim, S. H., MatJafri, M. Z., Abdullah, K. (2010). Landsat data to evaluate urban expansion and determine land use/land cover changes in Penang Island, Malaysia. Environmental Earth Sciences, 60, 1509-1521.
• Thapa, R. B., & Murayama, Y. (2010). Drivers of urban growth in the Kathmandu valley, Nepal: Examining the efficacy of the analytic hierarchy process. Applied Geography, 30(1), 70-83.
• Wang, N., Chang-Lin, M., & Yan, X. D. (2008). Local linear estimation of spatially varying coefficient models: an improvement on the geographically weighted regression technique. Environment and Planning A, 40, 986-1005.
• Wang, Q., Ni, J., & Tenhunen, J. (2005). Application of a geographically weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Global Ecology and Biogeography, 14, 379-393.
• Windle, M. J. S., Rose, G. A., Devillers, R., & Fortin, M-J. (2010). Exploring spatial non-stationarity of fisheries survey data using geographically weighted regression (GWR): an example from the Northwest Atlantic. ICES Journal of Marine Science, 67, 145-154.
• Yu, D. L. (2006). Spatially varying development mechanisms in the Greater Beijing area: a geographically weighted regression investigation. Annals of Regional Science, 40, 173-190.
• Zhang, L., & Shi, H. (2004). Local modeling of tree growth by geographically weighted regression. Forest Science, 50(2), 225-244.
• Zhao, F., Chow, L., Li, M., & Liu, X. (2005). A Transit ridership model based on geographically weighted regression and service quality variables. Report DO97591, Lehman Center for Transportation Research, Department of Civil and Environmental Engineering, Florida International University.