Dengue Influx Management And Analysis Tools (Dimat) For Prediction Modelling And Simulation

Zahidah Md. Shah ,
Ruhaiyem Nur Intan Raihana

Abstract

Dengue virus infection is the most rapidly spreading disease in the world. The prevention and control of dengue has become great public health challenge for many countries. The main objective of this research is to provide a real-time dengue prediction modeling and simulation based on the current cases within Malaysia through web-based application. Users which can benefit from the application is the normal user and experts. With this aim, we propose Dengue Influx Management and Analysis Tools (DIMAT), a web-based to simulate dengue disease and its vector’s dynamics that contains modelling and simulation which help us to understand epidemic dynamics and create scenarios to support planning and decision-making processes. Besides, DIMAT also features a real time dengue information for every state in Malaysia; daily monthly and yearly. Key advantage of DIMAT is that it is a user-friendly web application which developed to ease and assist the model configuration.

Keywords: Dengue prediction analysisprediction modellingsimulationweb-based application

Introduction

Dengue; a vector-borne disease, has become a viral infection and occurs in tropical and subtropical areas. Almost 100 million cases of dengue fever and half a million cases of dengue haemorrhagic fever (DHF) occur worldwide. The main vector that caused dengue when transmitted to humans through the bite of an infected mosquito is called the Aedes aegypti mosquito. There are four distinct serotypes of the dengue virus (DEN 1, DEN 2, DEN 3 and DEN 4). In Malaysia, to date, people are only aware on the number of dengue cases when we were informed based on the reported cases through news, hospitals, and website such as iDengue ( 2019); Malaysia’s main portal for reporting dengue cases and hot areas. This project is about a web-based application for dengue prediction within Malaysia. The project called Dengue Influx Management and Analysis Tools (DIMAT). DIMAT aims to provide resources to support and encourage the study of the spatiotemporal dynamics of dengue through modelling and simulation. This application is developed with a server with input such as human population, human that has been infected with dengue, human that has been recovered. Programming languages such as PHP, HTML, CSS, JS, MYSQL are used in DIMAT web application.

Problem Statement

Dengue is the disease that can cause death. Therefore, the prevention is one of effective way to control the disease. Therefore, a system to predict this dengue disease is highly needed. There was a web application such as Break Dengue that already collect data about who infected by dengue and display the result in their web application, but the result was not in details about the analysis part that predict the dengue and display the result of analysis on web application.

Research Questions

Two research question were formed based on the research statement discussed above:

  • How can this web-based application benefits different types of users with different background?

  • How can prediction modelling and simulation of expected dengue cases help researchers in their research?

Purpose of the Study

The objectives of the system are to provide dengue prediction that can be understand even by people who have less background on dengue history in Malaysia, to make ease for people that do research or work related to dengue to do prediction analysis through modelling and simulation. Besides that, the system also has the ability to provide a real-time dengue cases updated in iDengue ( 2019) Malaysia portal. In short, this web-based application has the same information as in iDengue ( 2019) and also the prediction function to ease researcher and public users do research or do simple prediction of dengue in the selected area in Malaysia.

Research Methods

Modelling tools is used to cast the observed dengue phenomenon into a mathematical description. The observed dengue phenomenon is too complex to be fully described fully, and thus mathematical description is needed to simplify this phenomenon of dengue. The model is a simplification of the reality ( Schickinger & Heilmann, 1993). Modelling tools is important for dengue prediction. By having such prediction tools, the analyst may know before the dengue virus attack an area. Result of the analysis will also help doctors and hospital to be ready to face dengue virus attack. Thus, the developed system provides three best modelling tools for dengue prediction.

Dengue Prediction Tools

There are three types of theories and algorithms of each of the modelling tools used in this development are discussed.

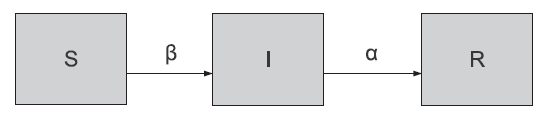
Susceptible Infected Recovered Basic Model (SIR Basic Model)

The SIR mathematics model which is based on susceptible, infected and removed (SIR) model of infectious disease epidemiology; simulates the spread of serotypes 1 of dengue virus between host and vector. The human population (N h) is divided into three groups; first is susceptible (S h) means people potentially get infected, second is infected (I h) means

people who are already infected, and removed (R h) means people who have recovered. Other parameters show the transition period from susceptible to infected (beta) and from infected to recovered (gamma) ( Side & Noorani, 2013).

Algorithm of SIR Basic Model: ( Langan, 2017):

n e w _ i n f e c t i o n = b e t a * ( S h * I h * N h )

i f n e w _ i n f e c t i o n > S h s o n e w _ i n f e c t i o n = S h

R h = R h + ( g a m m a * I h )

I h = I h + n e w _ i n f e c t i o n - ( g a m m a * I h )

S h = S h - n e w _ i n f e c t i o n

N h = S h + I h + R h

Susceptible Exposed Infected Recovered Basic Model (SEIR Basic Model) (SIR Basic Model)

The SEIR model is an extension of the classical SIR (Susceptible, Infected, Recovered) model which was originally developed 1927 (Figure 01 ): a fourth compartment is added which contains exposed persons which are infected but are not yet infectious ( Langan, 2017), where the fourth human population added was named people who shows exposed of virus infection (E h) ( Herawan, 2010).

Figure 1: Structure of the SIR Basic Model ( Langan, 2017)
Structure of the SIR Basic Model ( Langan, 2017)
See Full Size >

Algorithm of SEIR Basic Model:

N h = S h + E h + I h + R h

S h = S h - ( b e t a * S h * I h * N h )

E h = E h + b e t a * S h * I h * N h - ( s i g m a * E h )

I h = I h + s i g m a * E h - g a m m a * I h

R h = R h + g a m m a * I h

Susceptible-Infectious-Removed – Susceptible-Infectious Basic Model (SIR-SI Basic Model)

Another extended version of the SIR model is called SIR-SI Basic Model (Figure 02 ). The population is divided into three classes for humans and two classes for mosquitoes or vectors that transmit the disease. For human; S h, I h and R h are used. Similarly, S v and I v represents the proportion of mosquitoes currently susceptible and infected respectively.

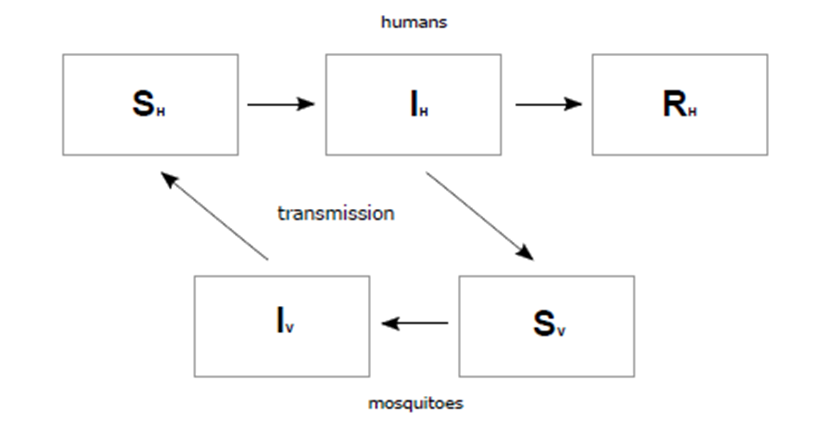
Figure 2: Structure of SIR-SI Basic Model ( Boret, Escalante, & Villasana, 2017)
Structure of SIR-SI Basic Model ( Boret, Escalante, & Villasana, 2017)
See Full Size >

Algorithm of SIR-SI Basic Model: ( Boret et al., 2017):

n e w _ h u m a n _ i n f e c t i o n s = ( b e t a * b i t t i n g / N h ) * S h * I v

if n e w _ h u m a n _ i n f e c t i o n s > S h ,

then n e w _ h u m a n _ i n f e c t i o n s = S h

n e w _ v e c t o r _ i n f e c t i o n s = ( b e t a * b i t t i n g / N h ) * S v * I h

i f n e w _ v e c t o r _ i n f e c t i o n s > S v t h e n n e w _ v e c t o r _ i n f e c t i o n s = S v

R h = R h + ( g a m m a * I h )

I h = I h + n e w _ h u m a n _ i n f e c t i o n s - ( g a m m a * I h )

S h = S h - n e w _ h u m a n _ i n f e c t i o n s

N h = S h + I h + R h

I v = I v + n e w _ v e c t o r _ i n f e c t i o n s

S v = S v - n e w _ v e c t o r _ i n f e c t i o n s

N v = S v + I v

Summary

This section will summarise the similarities and differences of eight variables between the three dengue prediction models through Table 01 . All three models have their own variables depending on the availability of real data of each variable.

Table 1 -
See Full Size >

Findings

This section provides the result status of provided functions in DIMAT (Table 02 ) which were based on numerous testing of different ‘project’. Table 03 tabulated a critical evaluation of the system in terms of advantages, disadvantages, limitations and strengths as compared to existing system or applications. All data in function testing was gathered from about 50 different users (i.e. trials/tests).

Table 2 -
See Full Size >
Table 3 -
See Full Size >

Conclusion

As a summary, the DIMAT website is a success. Most of the functions that were proposed at the early stages of the development have been executed and developed successfully. In future, DIMAT website can be further improved with these suggested list; increase the data collection on dengue cases occurs every day and every single area or district and add other modelling tools in this website. DIMAT can be viewed and easily understood by public users that does not work related to dengue. They can view dengue cases every day and can be more alert on dengue cases in selected areas. Moreover, DIMAT also make useful for medical doctors and/or researchers to do prediction, analysis, comparison, modelling and simulation on dengue cases.

Acknowledgments

The authors wish to thank Universiti Sains Malaysia for the support it has extended in the completion of the present research through Bridging University Grant No.: 304/PKOMP/6316502.

References

Copyright information

Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

About this article

Publication Date

30 March 2020

Article Doi

https://doi.org/10.15405/epsbs.2020.03.03.76

eBook ISBN

978-1-80296-080-8

Publisher

European Publisher

Volume

81

Print ISBN (optional)

-

Edition Number

1st Edition

Pages

1-839

Subjects

Business, innovation, sustainability, development studies

Cite this article as:

Md. Shah, Z., & Intan Raihana, R. N. (2020). Dengue Influx Management And Analysis Tools (Dimat) For Prediction Modelling And Simulation. In N. Baba Rahim (Ed.), Multidisciplinary Research as Agent of Change for Industrial Revolution 4.0, vol 81. European Proceedings of Social and Behavioural Sciences (pp. 657-663). European Publisher. https://doi.org/10.15405/epsbs.2020.03.03.76

Copy citation text