Development Of Information Processing Skills On Mathematics Lessons At Primary School

Abstract

The article describes the possibility of development of certain general learning actions that characterize the information literacy of junior students. It considers the actions: to search for data in a mathematical task; provide information in a predetermined or independently selected form (a text, a table, a picture, etc.); interpret the information obtained when solving the task as a response, a conclusion, or an explanation. The article also presents some results of TIMSS tests of 2011 and 2015, that allowed to highlight difficulties of Russian schoolchildren in performing mathematical tasks because of lacking skills to work with information. It describes three pedagogical conditions of the successful development of younger students ability to work with information using means of the subject "Mathematics" in the primary school: the designation of common mathematical and information literacy skills and actions; the help to a pedagogue in the development of the said skills in the study of different sections of the course; the use of the group work to motivate and maximize the involvement of children in the learning activities. Three stages of the organization of work are proposed to prevent and eliminate difficulties the students face while working with information. The first stage provides for a team work on the search of all the data given by a mathematical task; the second stage is about making sets of exercises by students that are similar to the proposed assignment; and the third one includes the review of the solution and an explanation of mistakes.

Keywords: Informationmathematicsgroup workprimary school

Introduction

The development of skills to work with the information obtained in the classroom and in everyday life by the modern younger scholar is one of the fundamentally important task of the education. The primary education researchers (N.F. Vinogradova, N.B. Istomina, M.I. Kuznetsova, L.G. Peterson, A.L. Chekin) distinguished among the main characteristics of the modern students the ability to adequately and competently use reading, informational, and general cultural skills to solve learning tasks and everyday issues. The totality of these and subject (mathematics and natural science, and others) skills represents the functional literacy of the student. It is an important result of teaching the child that determines his readiness for further training and development. The information literacy is one of its central integrative (not tied to a substantive content of training) components. It includes: "awareness of the need to expand own information field; ability to navigate in the data stream; a set of skills, providing for: a) an effective research, selection, interpretation and use of information in accordance with the learning task or an everyday problem; b) the analysis, critical evaluation of the accuracy and reliability of selected information based on ethical norms of its use» (Vinogradova, 2017, p. 33). By information we mean "information about ... objects, facts, events, phenomena and processes, regardless of their form of presentation, reducing the degree of uncertainty, incomplete knowledge of ... objects, facts ..." (Polonskiy, 2017, p.526), and by the influence of information - solving of a specific task, related to working with data, information, etc., by a student. This article focused only on the following specific information activities that the child learns to perform in elementary school: to search for data in the proposed training (in the case - mathematical) task, to present information in a given or self-chosen form (text, spreadsheet, drawing and etc.); interpret the information received therefrom in the form of an answer, conclusions or recommendations. The work with the information is carried out in the study of any section of the course. The primary education standard (Federal'nyj gosudarstvennyj …, 2017) states that the information must be developed while working with any educational material. For example, while studying the text tasks on the motion, the student identifies known and unknown data, reads the table containing the motion data (the velocity of objects, the duration of the movement, the distance covered), selects or takes into account the proposed unit quantities, concludes on the type of the motion of objects using a picture (e.g. "catches up - runs"), etc. The study of geometrical material is accompanied by a child's ability to use the information about the objects to be measured, measuring instruments (ruler, tape measure, reticulation), the willingness to read the picture or drawing, create his own. All of these actions directly influence the quality of the solutions of mathematical (and not only) tasks by the student. At that, the result obtained by the junior student when solving a learning task is most often estimated only from the standpoint of matching the reference response (presented, for example, in the responses to the textbook, guidelines for teachers). The choice and consideration in dealing with the data presented in different parts of the task (and subject to the issue, in the text and in the figure or table, etc.), as well as the presentation completeness in addressing all phases of the argument (the image, structures) are not taken into account and evaluated; there are no demands to the level of detail in conclusions made by a junior student. It is clear that such requirements should not be placed for the final assessment of a student achievements, however, in the daily work they are necessary for the routine control and the timely help to students in case of difficulties, or for the inspiration of more successful children to find new solutions and ways to present their achievements.

Problem Statement

The article considers the following pedagogical conditions for the successful development of younger students’ skills to work with information using "Mathematics" subject means. The first one is the selection of common mathematical and information literacy skills and actions. These include reading, presentation, and interpretation of the mathematical task data. The second condition is the assistance to the pedagogue in the development of the selected skills in the mathematics lessons covering different sections of the course, the use of group work to motivate and maximize the involvement of children in the learning activities. The objective for the teacher in this work is the development of these skills as general learning skills, rather than narrow-subject ones required to perform particular tasks. Therefore, teachers need methodological assistance in the organization of the work with information on math lesson.

Research Questions

The article discussed the importance of mathematical skills to form the subject actions necessary to work with the information. It presents the contribution of the group and paired types of interaction between students on math lesson in the development of universal actions characterizing the information literacy of the student.

Purpose of the Study

The objective of the article is to demonstrate the contribution of a particular subject content of the course "Mathematics" for the primary school in the development of subject information actions - information search, the presentation of information in a given or a self-chosen form, the interpretation of the results or solutions obtained in the form of reasoning output. This article contains comments for teachers on the organization of the work with information in the course of group and pair work on a math lesson.

Research Methods

While preparing the article, the author studied theoretical material and analyzed the practice of modern primary school in the area of the information skills development by children, as well as the experience of the pair and group activities of junior schoolchildren. The author performed the comparative analysis of data of tests conducted under TIMSS international comparative study (Trends in Mathematics and Science Study) in 2011 and 2015 and highlighted several possible reasons for the declining efficiency in the performance of certain tasks. The article also provides for the description of the experimental work on the use of various types of group and pair interaction of students in the classroom to develop the skills to work with information.

Findings

So that a student could freely use the informational skill in different classes, it is necessary not only to generate such skill on a particular lesson, but also help students to gain experience first through the use within a single object, and then on others. This article covers only the issue of how to help students apply these skills when working with different themes of the mathematics.

Obviously, the study of math comes easy not for all children, and it is important that the pedagogue created a learning environment in the classroom that would motivate children to search, take initiative and act independently. To create such an atmosphere the pedagogues often use different types of the training organization - the front (the collective) type, groups, pairs. Teachers are not limited to the telling the material or offering students to read the text of the textbook and involve children in the discovery of new knowledge through the participation or with the assistance of classmates. The accumulation of experience together with the teacher and classmates activity goes in parallel with the accumulation of techniques to work with the information: the student observes and repeats the action performed by the adult and other students; understands and uses different search techniques, design solutions; appreciates the importance of own actions for obtaining common solutions. The importance of the involvement of the child in collective work covering a specific educational problem was stressed by the famous domestic pedologue P.P. Blonsky, whose work addressed the theme of children's leadership in the learning process (Kotelnikov & Senchenkov, 2019): working together encourages each student to be involved in the common work, choose and "collectively distribute the various aspects of this work" (Blonskij, 1919, p.88). The professionalism of the teacher in this case is "to trigger the own organizational force of children from inside, rather than from outside and arbitrarily far-fetched (Blonskij, 1921, p.84). Thus, the group work in math class can be used for the development and putting together (for further transfer to other work with different contents) of informational skills.

Let’s outline the main problems of junior school students in the demonstration of skills that characterize the ability to work with information (data research, reporting and interpreting the received information in the form of arguments, responses). According to the results of international comparative study TIMSS 2015, the four most common difficulties for Russian fourth-graders are:

• errors in tasks which are not based on the material studied in math class;

• misunderstanding of the wording other than the one conventionally used;

• inability to explain their own answer;

• difficulties in the selection (and use) of all data and reference relations in the text of the task (Kovaleva, Krasnyanskaya, & Rydze, 2018; Mullis, Martin, Foy, & Hooper, 2016).

Note that the causes of the first two difficulties is misunderstanding text of the task due to objective (a material was not studied, the task was unknown to the student) and subjective (inability to draw an analogy, put together or elaborate the available knowledge) reasons. A prerequisite for the third trouble may be that when performing tasks in the classroom, the priority is the receipt of a response or a result, rather than reasoning and the course of action. The fourth difficulty (work with all the data of an educational task) can be provoked by the lack of attention to the analysis of texts of educational tasks on the lesson, the hasty move of a child from reading to solving. As an example to illustrate the existence of problems in the teaching related to the underdevelopment of the ability to work with information, let’s consider the task of the TIMSS study for fourth graders, offered in 2015 and 2011.

The task was called "Circles and dots» (Mullis, Martin, Ruddock, O’Sullivan, & Preuschoff, 2014a, p.4). The following mathematical and information skills were tested:

math: have an idea of an equilateral hexagon; be able to establish the rule for making a given shape and connect the dots according to this rule;

information skills: use the information provided in the text, in the picture, as well as work with the information obtained during accomplishment of the task.

Fourth graders were required to allocate data in the text part of the task - "Build a hexagon in a circle, with equal sides" (conditions: it is required to draw a figure, a hexagon is to be built having the property - "all sides are equal"). Also, there was information in the picture (Figure 1 ), which also need to be taken into account to obtain a correct answer.

See Full Size >

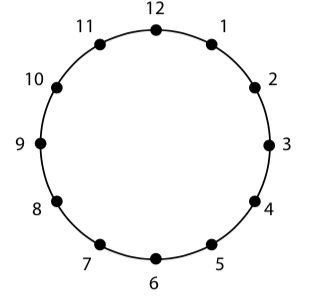
A student had to understand by this picture, that it is necessary to connect the dots in a certain order and then there will be a hexagon with equal sides. If the child had taken into account all this data and used the training part of the task in which it was necessary to see that if the dots are connected to the rule "three" (3,6,9,12,3), it will come to the square - quadrilateral with equal sides, then the task was done right. In 2015, 61.8% of Russian fourth graders coped with the task (among all the participating countries, the average result - 43%). If at least one of the above conditions was not taken into account ("hexagon", "equal sides", "rule for connection of the points", "drawing a square in the training part"), it was impossible to get the right answer. Thus, the loss of even one condition of the task hindered the student from demonstrating his mathematical skills. However, these skills are developed by fourth-graders: any primary school graduate distinguishes polygons, may indicate those among them that are equilateral, is able to establish an elementary rule of order (connection points "through one") and draw on the points. I.e., the primary school children should not have difficulties to perform mathematical actions. At the same time, there is a concern that in 2015, children coped with this task poorer than in 2011. In 2011, 77% of Russian students performed it correctly. Analysis of other jobs in which t our students were less successful than in 2011, allows to suggest that when solving the task, children did not take into account one or more conditions of the task, which led to a partially correct or a wrong decision. Scientific works of pedagogues and psychologists involved in the comparative analysis of the results of national and international studies, quality evaluation of subject and general educational achievements (Kovaleva et al., 2018; Vinogradova, 2017; Sahlberg, 2015; Lompscher, 1999) point to the importance of conducting a comparative analysis of the results at different times and for different subjects, highlighting common characteristics (skills, actions, student motivation).

We offer several methods of organization of work in the classroom to prevent and resolve difficulties in in the work of school students with information. For convenience, we shall illustrate the techniques through group work with a leader and democratic interaction. Leader interaction involves the appointment or choice of the student within the group, who will organize the actions of classmates and present the results. In a democratic interaction, school students (we will describe only the work of fourth-graders) do agree on the distribution of assignments and presentation of results of activities. A particular case of the collaboration - a work in pairs which involves the teacher and the student having academic problems in learning - is also presented below. The tasks discussed below were tested in math class in experimental schools of the laboratory of the general primary education (led by Professor N.F.Vinogradovа) of the Institute for Strategy of Education Development of RAE.

Method 1 . The search of all data of mathematical tasks by the team of students. This technique can be used in the study of any branch of mathematics course.

An example of groupwork with democratic interaction. "Consider Picture 1 (see above). In what order you need to connect the dots to get a dodecagon, hexagon? For each case, write down a rule and take the picture. "

Comment. The task refers to the section of the mathematics "Geometric Shapes", but for its successful fulfillment the students will need to remember how the rule should be drawn up and recorded ("Numbers" section). The task execution can be successful if the children work together to highlight all the task conditions (consider Picture 1, come to a conclusion as a result of analysis of the task text that they need to create two rules and draw two figures), agree on who will make the rule for the hexagon, and who will do so for dodecagon; agree upon the rules entry ("connect the dots by one, starting from 12 - build a hexagon", "connect all the points in the order from 12 - build dodecagon") and will present the results of their work. During the discussion of the responses the teacher will ask questions to make sure that all task conditions were taken into account. For example, "How many rules you have made?", "Why you did not limit yourselves to one rule?", etc. If in this assignment the focus is shifted to the development and the presentation of the rules of drawing figures, then we can talk about attention to the development of such information skill as the interpretation of the results of reasoning, solution.

Method 2 . Students prepare a set of tasks similar to the proposed task.

Example. "Guys, come up with three exercises of your own, similar to such a task:

Picture 1 (see above) Galina connected the dots 3, 6, 9, 12, 3. What kind of figure she got? What is the property of this figure?

• Exercise 1________________

• Exercise 2________________

• Exercise 3 _______________ "

Comment: This assignment also applies to the "Geometric Shapes" and "Numbers". It is possible to organize work on it in groups with a leader interaction. The student who will act as a leader, will distribute assignments (one member of the group is responsible for any exercise), will determine the overall work strategy, will help to agree on what the figure will be created in each exercise and which property it will have. For example, a triangle with an obtuse angle can be done according to the rule: "connect dots 12, 2, 10, 12 '. If there are students in the class who have difficulties in learning mathematics, then one or more of them can be paired with a teacher (in this case the teacher acts as a leader in several pairs with his participation). The teacher will encourage the student of his "pair" to find a basis for the exercise - the construction of geometric figures in a circle - as a result of the analysis of condition of the task about Galina. He will help to check that all the requirements to the solution are met: 3 exercises, their similarity to the task.

Method 3 . The review of solutions and the explanation of errors. When organizing the work with information, it is necessary to demonstrate to students the ways to present the information that they receive in the course of study. All students face their own mistakes. Some errors are found by the children during performance of the task, other errors become familiar to them upon receipt of their work reviewed by the teacher. It is important that the younger school student learned not only to see the errors, but also to explain them and look for ways to eliminate. It is well known that it is rather difficult for people to reveal their own mistakes, while it is much easier to find mistakes of others (their classmates, the teacher). This method should help to solve two problems. Math - to search for and correct substantive errors; the problem of working with information - keep searching for an error in the different parts of the solution when it is presented in a different form.

Example task. Ivan solved 2 tasks. Find and explain all the mistakes he made. Ivan’s answers are written in italics.

Task 1 (Rydze & Krasnyanskaya, 2019). The bus had 35 passengers. On the bus stop 14 passengers left and 12 passengers entered in. How many passengers are in the bus? Point two correct solutions.

Solution 1: 35 – (14 – 12)

Solution 2: 35 + (14 – 12)

Solution 3: 35 – 14 + 12

Solution 4: 35 – 14 – 12

Ivan's answer: Solution 1.

Task 2 (Mullis, Martin, Ruddock, O’Sullivan, & Preuschoff, 2014b, p.5). What is the number closest to 300?

1) 275 2) 320 3) 307 4) 291 (Ivan’s choice)

Analysis of Ivan’s work.

Ivan made a mistake in performing the task _____.

Mistake explanation: _________________________________________.

Comment. The group or pair work focuses on the presentation of information, received during the discussion, in a special form. This is important because often the teacher and students only record the fact of a mistake. In order that a mistake is not repeated in the future (and in this task there are examples of standard errors), it is important not only to identify it, but also to discuss reasons relevant to children of a particular class and fix them in any form. This will help to prevent those mistakes in the future.

In the first task Ivan’s mistake was that he marked only one of the two correct solutions. The explanation can be written as "did not take into account the condition of the task - "Mark two correct solutions." The second task was performed by Russian students under the TIMSS study and coped with it - chose answer 307 - only 43% (Mezhdunarodnoe …, 2017). Ivan’s choice - response 291 - is the most common mistake, a possible reason is that children do not reflect on it. Proper reasoning could be as such: "From the number of 275 to 300 there are 25 units on the line, from 291 to 300 there are 9, from 307 to 300 only 7, from 320 to 300 more - 20. So the closest number to 300 is 307. "

Due to the fact that at present the use of information skills in different classes is not regulated by the methodology of primary education, it is necessary that the teacher included tasks on the work with information himself. Normally, they are not presented as separate tasks, but can identified from those available by the teacher. For example, if you need to work with an exercise containing a condition in the text, in the picture, in the table it is possible to propose the preliminary task. For example, this one: "Read. What information can be obtained using a table? The table and the picture? The table, the picture and the text? ","What questions cannot be answered only on the basis of the picture?".

Information skills are used in every class at school, but not always the student himself can characterize them and to apply correctly, and is not always ready to apply informational actions, mastered in other lessons, on math. The study conducted in the laboratory of the general primary education of the Institute for Strategy of Education Development revealed that a student's ability to see how the knowledge or skills acquired in one class is used on another one positively influences the overall performance. For example, the ability of children to rank numbers helps them to successfully arrange words in alphabetical order, and vice versa, if the teacher draws the attention of children to the fact that arranging words in alphabetical order is effected under the same algorithm as ranking numbers, this increases the performance of such tasks. Using tables on the science lessons, that were studied within the framework of the relevant topics in the math lessons, helps to summarize knowledge (group in rows and columns), to compare objects of the environment (rows and columns) (Vinogradova & Kalinova, 2019).

Conclusion

The study highlighted and described the approaches to improve the quality of primary mathematical education by the following means: taking into account the difficulties of students in performing mathematical tasks due to underdeveloped skills to work with information, features of most relevant informational skills, the choice of the type of students interaction within the group, the use of the sets of mathematical tasks. It demonstrated methods of work of the teacher in the classroom, which increase the motivation and interest in the use of informational skills by children to solve mathematical tasks. The methodical commentary is given on the course and results of performance of the specific tasks by fourth-graders at work in groups or in pairs with a teacher.

The proposed methodological procedures and comments can be used by teachers, methodologists and other experts in the primary education for the development and monitoring the progress of younger school students’ skills to work with information. The identified deficient math skills (taking into account all conditions of the task, explaining the received answer or a solution) can be improved in the course of the work on development of informational skills (searching and considering all data when dealing with the educational task, the presentation of information in different forms, the interpretation of results). The teacher can use different forms of interaction between students to enhance the task performance, the accumulation of the positive educational experience by students, the elimination of typical mistakes.

Acknowledgments

The work has been done within the framework of the state assignment to FSBSI "Institute for Education Development Strategy of the Russian Academy of Education" No. 073-00086-19-01 for 2019 and the planning period of 2020 and 2021. Project "Scientific and methodical bases of creation of sector strategy of the development of education in the Russian Federation and the mechanisms for its implementation (within the purview of Ministry of Education of Russia)."

References

1. Blonskij, P. P. (1919). Trudovaya shkola. [Labour school]. M. Moskva: Lit.-izd. otd. Nar. kom. po prosveshcheniyu.
2. Blonskij, P. P. (1921). Trudovaya shkola. [Labour school] Vladivostok: Izdatel'stvo Dal'nevostochnogo kraevogo soyuza zemstv i gorodov.
3. Federal'nyj gosudarstvennyj obrazovatel'nyj standart nachal'nogo obshhego obrazovanija [Federal state educational standard of the primary general education]. (2017). M-vo obrazovanija i nauki Ros. Federacii. M.: Prosveshhenie, 53 р. [in Rus.].
4. Kotelnikov, A. V., & Senchenkov, N. P. (2019). Pavel Blonskiy’s ideas about children’s leadership. Pedagogika, 7, 103-109.
5. Kovaleva, G. S., Krasnyanskaya, K. A., & Rydze, O. A. (2018). Rezultaty` vypolneniya diagnosticheskix rabot po matematike, russkomu yazyku i chitatelskoj gramotnosti uchashhimisya 5-x klassov. [Results of performance of diagnostic tests on mathematics, Russian language course and reading literacy by 5th-graders]. Moscow: ISRO RAO.
6. Lompscher, J. (1999), Motivation and activity. European Journal of Psychology of Education, 1, 11-21.
7. Mezhdunarodnoe issledovanie po ocenke kachestva matematicheskogo I estestvennonauchnogo obrazovanija. [International study on the assessment of quality of education in mathematics and science]. (2017). Retrieved from: http://www.centeroko.ru/timss15/timss15_pub.htm
8. Mullis, I. V. S., Martin, M. O., Ruddock, G. J., O’Sullivan, C. Y., & Preuschoff, C. (Eds.) (2014a). TIMSS-2015. G4_Booklet_1. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College.
9. Mullis, I. V. S., Martin, M. O., Ruddock, G. J., O’Sullivan, C. Y., & Preuschoff, C. (Eds.) (2014b). TIMSS-2015. G4_Booklet_5. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College.
10. Mullis, I. V. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS-2015: International Results in Mathematics. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College.
11. Polonskiy, V. M. (2017). Bol'shoj tematicheskij slovar' po obrazovaniyu i pedagogike. [Large thesaurus on education and pedagogy.] M.: Narodnoe obrazovanie.
12. Rydze, O. A., & Krasnyanskaya, K. A. (2019). Matematika. 4 klass. Podgotovka k Vserossiiskoi proverochnoi rabote (VPR). Raznourovnevye proverochnye raboty. Uchebnoe posobie. [Maths. 4th grade. Preparation for the CDF. Multilevel examination tests. Tutorial.] M.: Ventana-Graf.
13. Sahlberg, P. (2015). Finish Lessons: What Can the World Learn from Educational Change in Finland? New York: Teacher College Press.
14. Vinogradova, N. F. (2017). Koncepcija nachal'nogo obrazovanija: “Nachal'naja shkola ХХI veka” [Concept of the primary education: “Primary school of XXI century”]. M.: Ventana-Graf.
15. Vinogradova N. F., & Кalinova, G. S. (2019). Independent Work of Pupils at the “World around us“. Nachal'noe obrazovanie, 3, 43-47.