Abstract
Imagination is a necessary cognitive function of everyday human activity and a prerequisite for creative thinking. We can distinguish spatial, geometric, or planar imagination but there is no clear boundary among them. In this paper, we are interested in planar geometric imagination and its development as an educational goal for student teachers at primary schools and kindergartens. Nowadays, pupils are required to develop critical thinking, be creative and be able to orientate themselves in today's world of information and images. But the same must be demanded for current student teachers training as well. There is still the concept that geometry is about drawing only. Our research covered 72 students (studying Teaching at Lower Primary Schools and Teaching at Kindergartens) of the Faculty of Education of the University of Hradec Kralove in the Czech Republic. The level of planar imagination was determined on the basis of standardized Vonkomer’s PFB planar imagination test. We measured this level at the beginning of the geometry course and at the end. In the course of geometry, students were introduced to various methods and means of teaching geometry. We also investigated whether there is a relationship between the level of plane imagination and the individual interest of students in art or playing various games in their extracurricular time. The correlation between these variables has not been demonstrated, but the positive effect of the one-semester course of geometry on the result of the planar imagination test has been proven.
Keywords: Primary educationpreschool educationmathematicsimagination
Introduction
Primarily, imagination is a cognitive process. Sternberg (Sternberg, 2002) states that imagination is an important inner process in orientation in the outside world, in decision-making and action. Therefore, the images are mental representations of those things that are not perceived by sense organs at the moment of representation. The key cognitive process involves mental representations in all sensory modalities. Visual images have all the properties of real objects in the world. They are located in a kind of mental space and these objects are mentally moved or rotated (Eysenck & Keane, 2008). Imagination is a prerequisite for creative work (Hartl, 1994).
In this paper, we will be interested in imagination in the context of mathematical abilities. The global component of imagination-related mathematical skills is the ability to think logically in the sphere of quantitative and planar relationships. The general synthesizing component that influences the type of mathematical thinking is spatial imagination (Kosc, 1972). According to Kosc (1972), one of the factors of mathematical abilities is the spatial factor. This term means the ability to perceive spatial relationships, to orient in space, or the ability to manipulate real or somehow represented material in the visual field. Furthermore, this factor involves the ability to capture purposeful and deliberate changes in the visual properties of the presented or specific objects or structures. This factor is, therefore, significantly involved in the correct solution of problems mainly in the field of geometry.
Imagination and mathematical abilities
For the purpose of defining spatial imagination in the field of geometry, Josef Molnar formulated the expression of spatial imagination as a set of abilities related to reproductive and anticipatory, static and dynamic images of shapes, properties and interrelationships among geometric shapes in space (Molnar, 2009). The planar geometric imagination is a type of spatial imagination. The objects of the idea are geometric shapes in one plane, but in some cases, we move into mental manipulations of these shapes in space.
Spatial and planar imagination is developed on the basis of genetically conditioned and innate talents. This development is done by maturation and learning, which is influenced by the individual's own activities, environment and education. Spatial and planar imagination can be deliberately developed at preschool age as well as in adulthood. The teacher plays an important role in the development of spatial and planar imagination. It significantly depends on the teacher, in what form, what types of tasks and how often he or she assigns such tasks to the pupils. If the teacher believes that he or she does not have a good level of spatial imagination, his or her role as a factor in the process of developing the pupil's imagination may be weakened (among other reasons). An overview of studies dealing with the relationship between the level of mathematical knowledge, teaching and the use of teacher’s methods of teaching is presented in (Aslan-Tutak & Adams, 2015)
The work of Cooper and Shepard was a boundary research on planar imagination in connection with mental rotation. Probands were presented letters and numbers in a normal or mirror-inverted form. Research participants of the experiment were asked to assess as quickly as possible whether the item is displayed in normal, or mirrored version. Test items were presented in several different orientations. The main result was to find out that the more the test item was turned against the standard vertical position, the longer it took the probands to make their decision (Cooper & Shepard, 1973).
Standardized test of planar imagination
A way how to determine the level of planar imagination is to use a standardized PFB planar imagination test. This test was developed in the USA and it has been used in Czechoslovakia since 1945 as a part of a mechanical capability test. Later, the test was modified by Vonkomer (2007); however, the difficulty of the tasks has not changed. The PFB test is also considered to be a technical imagination test (Vonkomer, 2007). The test consists of 56 tasks and it has a time limit of 15 minutes. Each task shows a certain geometric shape divided into several irregular parts. The task is to compose the intended geometric shape from these parts. Mental rotation, including flipping, or, in terms of geometry, opposite isometry, is used. It is important to realize that in case of flipping, spatial imagination is necessarily involved but we work with planar patterns in mind. Some tasks may have multiple solutions, as illustrated, for example, by an easy task in Figure
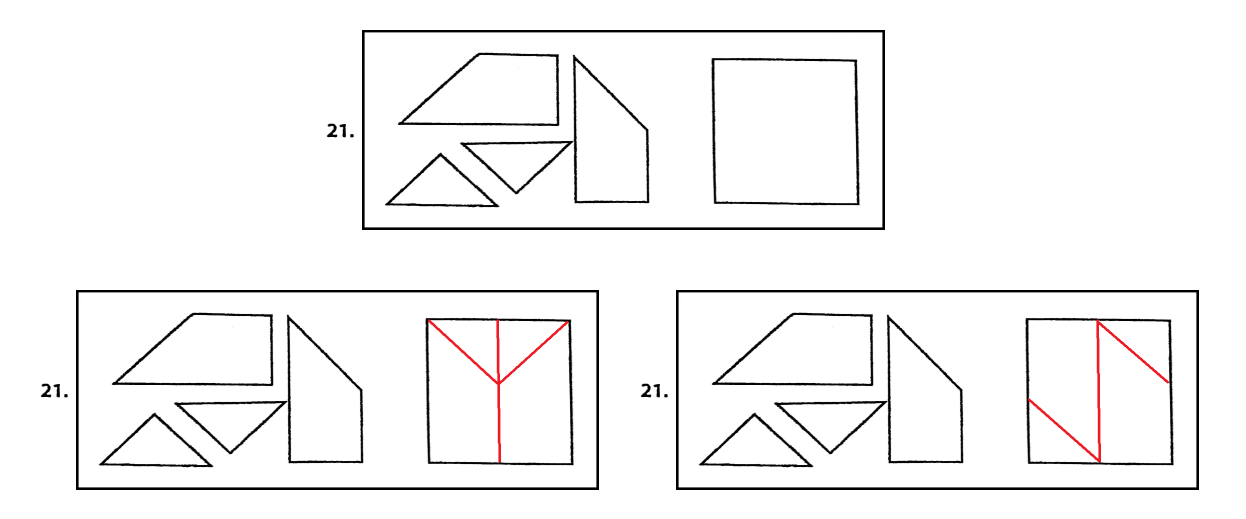
Problem Statement
We concentrate on findings focused on the level of planar imagination of primary and preschool teachers. It is obvious that, especially at primary school, the direction of education is significantly influenced by the teacher's personality.
The current curriculum of the primary stage of elementary education in the Czech Republic is directly aimed at the development of spatial imagination only within the chapter “Non-Standard Application Tasks and Problems”. But from my experience, I can say that planar and spatial imagination can be developed in any primary mathematics education curriculum, not only in geometry.
The publication called Critical Points of Elementary School Mathematics in Pupil's Tasks Solving draws attention to the low level of planar and spatial imagination. For example, in the design of constructional tasks, it has been found that emphasis is placed on the structure itself instead of analysis, which represents the moment of the idea. Sketches are taken as non-mathematical. Often, geometric shapes and tasks are given as prototypes, or "best" examples of a given category (e.g. the triangle is mainly equilateral, the parallelogram is primarily a rhomboid). The covering of the plane is not sufficiently mentioned, however, it is important for understanding the determination of the content of geometric shapes. Instead, the subject matter goes to algebraization as quickly as possible (Vondrová & Rendl, 2017).
Research Questions
We have asked these research questions:
What is the level of planar imagination of students of primary and preschool education?
What influence on the planar imagination of prospective teachers in primary school and kindergarten has the completion of the geometry course?
Do these prospective teachers achieve higher scores in Vonkomer's PFB Imagination Test if they have been educated in art at high school and if they are interested in visual arts?
Do these students achieve higher scores in Vonkomer's PFB Imagination Test if they play different games in different forms at extracurricular times?
Purpose of the Study
This study is a part of a dissertation thesis on visual arts and visual culture in teaching mathematics, where both imagination as a cognitive process and creativity are key notions. The main purpose of this study is to find out the level of planar imagination of student teachers and explore it from different directions. In addition, the findings in this study will be decisive for changing the quality of teaching geometry, algebra and arithmetic to primary school student teachers. It is equally important that the imagination in the context of the prematematical imagination of children is considered and taken into account when preparing kindergarten teachers. From ancient history, both artists and mathematicians have been researching the same natural phenomena. Since early childhood people have come to know natural and human creations through visual perception (and through smelling, touching, tasting, listening too). These experiences lead students to acquire the first mathematical concepts (Brezovnik, 2015). The article (Baker, 2013) is devoted to the positive impact of integrating art on cognitive development.
Research Methods
Participants of the study
The research involved 22 students of teacher training for kindergarten as a part of the course called Developing Mathematical Imaginations and 50 students of teacher training for primary school within the subject Geometry with Didactics. These subjects are taught by the author of this paper at the Faculty of Education at the University of Hradec Kralove in the Czech Republic.
PFB test and a questionnaire
The key element for the measurement was the standardized planar imagination test and additional data were obtained by a questionnaire with open questions. The planar imagination test was deployed at the beginning of each of the one-semester subjects mentioned above, and after three months at the end of the subjects. Students had no problem understanding the test.
In the first part, the questionnaire that the students received addressed their concept of creativity. The second part consisted of open questions about the type of high school attended, hobbies, extracurricular classes (if they had attended any before entering college). Furthermore, we were interested in games they play, including board or party games, computer or smartphone games.
We connect the results from the imagination test with selected data from this questionnaire. The concept of creativity of our students will be the subject of further research.
The content of the courses of Development of Mathematical Ideas and Geometry with Didactics
In these courses, the following material, which could in some way mediate the development of planar imagination, was taught in lectures and seminars:
basic and derived geometric concepts in the plane, types of lines
polygons
circle and disc
congruence and similarity of planar images
covering and dividing the plane
use of dynamic software to support teaching mathematics
construction toys, kits and games
Students in the seminars not only drew, derived algebraically, but also worked with paper (folded, cut), skewers, magnetic and other construction kits, and saw samples of dynamic geometry in GeoGebra computer software. Storytelling, manipulative activity, and a combination of multiple representations provide students with meaningful opportunities to engage induction thinking, synthesis, and creativity development in the mathematics class (Kim, Bae, Choi, Kim, & Lim, 2019).
Descriptive research on the level of planar imagination and testing its change
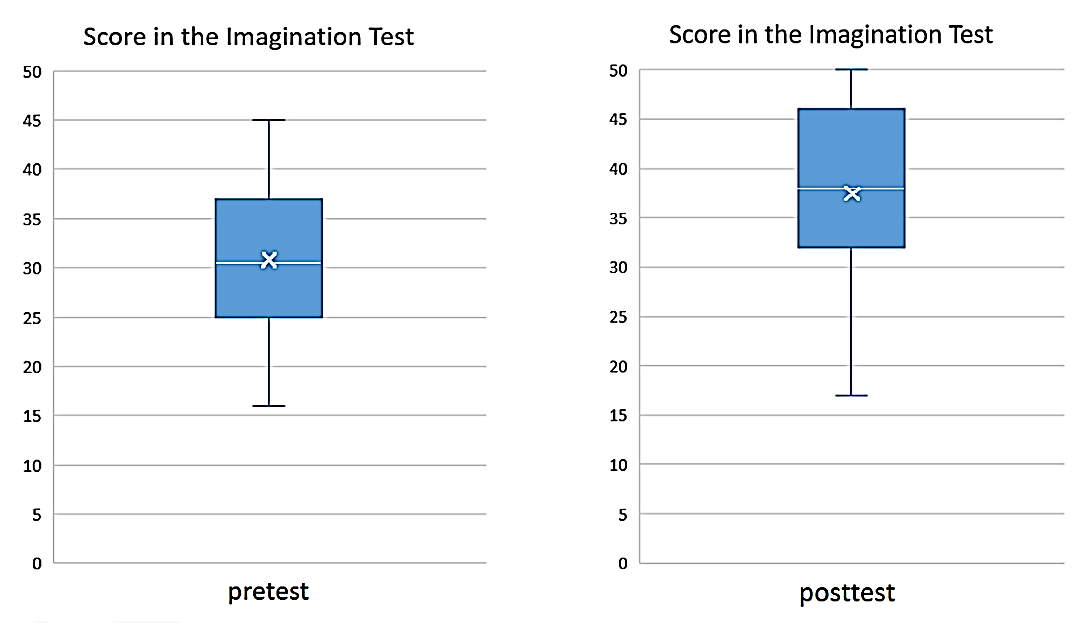
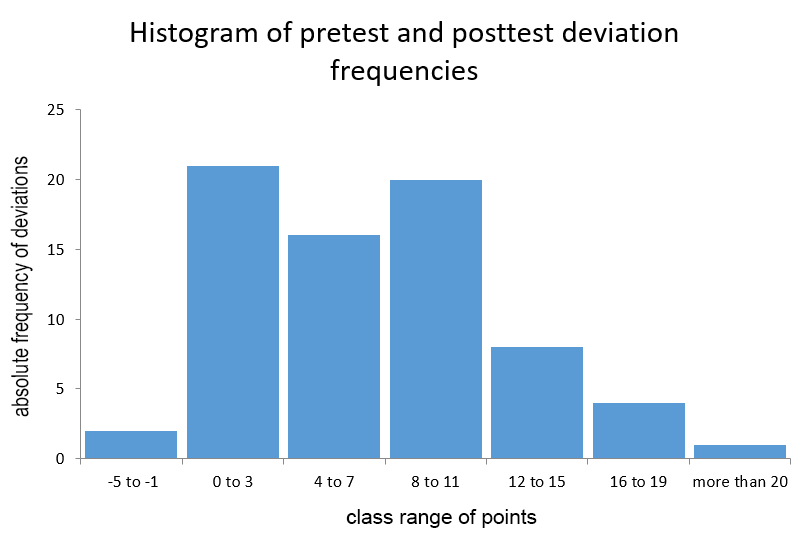
Using the Vonkomer’s test, we tested the level of planar imagination of students at the beginning of the geometry course (pretest), and then at the end (posttest). We calculated the descriptive statistics for both files, compiled their histograms and boxplots. We also calculated the deviations of the pretest and posttest points and constructed a histogram based on these deviations. The conclusion can be visually derived from the boxplots and from the deviation histogram.
The level of planar imagination and extracurricular activities in the art field
We assume that we definitely use imagination in activities such as drawing, painting, modelling, viewing, or conceptualizing. We were hence interested in answering the question of whether those who are, or were interested in arts achieve a better score in the imagination test. We consider pretest data as an input measurement of planar imagination. We use data from a questionnaire to evaluate out-of-school activities in the visual arts; specifically, to answer the following open questions.
What are your hobbies?
What hobby courses did you attend during high school?
Which art movements are close to you?
Based on the answers to the three questions above, we calculate the value of the "interest in art" as the sum of the following: for each item (sufficiently semantically different) given in the answer in each of the three questions above, we add one point. If one of the items “postmodernism, the 21st century art and the 2nd half of the 20th century” is mentioned in the third answer, then one extra point is assigned to the question. The relationship between planar imagination and extracurricular activities in the field of fine art can be found using the Spearmen correlation coefficient.
The relationship between planar imagination and extracurricular activities in playing logical or geometrically oriented games
The starting point for this relationship is the fact that many desktop, social, computer or mobile games develop various cognitive functions, mathematical, logical or strategic thinking (Milkova, 2008; Milkova & Sevcikova, 2017). As an input measure of planar imagination, we take the pretest data again. To evaluate out-of-school activities by playing games, we use the data from the questionnaire, specifically the following items:
If you play board games, name them.
If you play games on mobile devices, name them.
If you play computer games, incl. game console, name them.
We add one point for each listed game in response in each of these three items (board games, mobile phone games, computer games / game console). If there are related card games, they are scored one point only in total. We exclude games such as Ludo, racing and sports, shooter video games and knowledge games. The relationship between planar imagination and extracurricular activities in the field of playing logical or geometrically oriented games can be found using the Spearmen correlation coefficient.
Findings
By processing data on prospective teachers at the University of Hradec Kralove in the Czech Republic by various statistical methods, we received answers to the above-mentioned questions, some of which were quite surprising to us.
Looking at the boxplots of the pretest and posttest results in Figure
The histogram pretest and posttest deviation frequencies is shown in the following Figure
Regarding the relationship of interest in art and the results of the imagination test, from the rough outline of the questionnaire responses, we could have expected that the effect of this factor would not be very significant. It was also confirmed by the value of the Spearmen correlation coefficient (
Similarly, it has not been statistically proven whether there is a relationship between the results of the imagination test and the fact whether students play different games in their free time or not. The correlation coefficient in this case is
Conclusion
Imagination, in a different sense, is important for everyday activities. Spatial imagination tests are more used in intelligence tests or assumption tests. Though, in this paper, we were interested in the planar imagination, which shifts into the spatial imagination in certain tasks. We were wondering what could be linked to the evolution of the level of imagination. We found out that there is no statistically demonstrable correlation between a high score in Vonkomer’s PFB planar imagination test and the fact whether the students have been involved in artistic work, where imagination is important. Furthermore, there was no correlation between playing games in participant’s free time and his or her results of the planar imagination test. On the other hand, the geometry courses at the Faculty of Education contributed to increase the score from this test statistically for the entire selection.
Acknowledgments
The paper has been supported by Specific Research Project of the Faculty of Education, University of Hradec Kralove, 2019, Number 10/II.
References
- Aslan-Tutak, F., & Adams, T. L. (2015). A Study of Geometry Content Knowledge of Elementary Preservice Teachers. International Electronic Journal of Elementary Education, 7(3), 301-318.
- Baker, D. (2013). Art Integration and Cognitive Development. Journal for Learning through the Arts, 9(1), 1-15.
- Brezovnik, A. (2015). The benefits of fine art integration into mathematics in primary school. CEPS Journal, 5(3), 11-32.
- Cooper, L. A., & Shepard, R. N. (1973). Chronometric studies of the rotation of mental images. New York, NY: Academic Press.
- Eysenck, M. W., & Keane, M. T. (2008). Kognitivní psychologie [Cognitive Psychology]. Prague: Academia.
- Hartl, J. (1994). Psychologický slovník [Psychological Dictionary]. Prague: Budka.
- Kim, D. J., Bae, S. C., Choi, S. H., Kim, H. J., & Lim, W. (2019). Creative Character Education in Mathematics for Prospective Teachers. Sustainability, 11(6), 1730.
- Kosc, L. (1972). Psychologia matematických schopností [Psychology of Mathematical Abilities]. Bratislava: SPN.
- Milkova, E. (2008). Multimedia Applications and their Benefit for Teaching and Learning at Universities, WSEAS Transactions on Information Science & Applications, 5(6), 869-879.
- Milkova, E., & Sevcikova, A. (2017). Algorithmic Thinking and Mathematical Competences Supported Via Entertaining Problems. International Journal of Education and Information Technologies, 11, 80-86.
- Molnar, J. (2009). Rozvíjení prostorové představivosti (nejen) ve stereometrii [Development of Spatial Imagination (not only) in Stereometry]. Olomouc: Palacký University Olomouc.
- Sternberg, R. J. (2002). Kognitivní psychologie [Cognitive Psychology]. Prague: Portál.
- Vallo, D., Rumanova, L., & Duris, V. (2014). Spatial Imagination Development through Planar Section of Cube Buildings in Educational Process. Procedia – Social and Behavioral Sciences, 191, 2146-2151.
- Vondrová, N., & Rendl, M. (2017). Kritická místa matematiky základní školy v řešení žáků [Critical Points of Elementary School Mathematics in Pupil's Tasks Solving]. Prague: Karolinum.
- Vonkomer, J. (2007). PFB – Testová příručka [PFB - Test Guide]. Bratislava: Psychodiagnostika.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
07 November 2019
Article Doi
eBook ISBN
978-1-80296-071-6
Publisher
Future Academy
Volume
72
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-794
Subjects
Psychology, educational psychology, counseling psychology
Cite this article as:
Trojovska, E. (2019). Specifics Of The Planar Geometric Imagination And The Concept Of Its Development. In P. Besedová, N. Heinrichová, & J. Ondráková (Eds.), ICEEPSY 2019: Education and Educational Psychology, vol 72. European Proceedings of Social and Behavioural Sciences (pp. 360-368). Future Academy. https://doi.org/10.15405/epsbs.2019.11.34

