Mathematics For The Education Of The Engineers In The 21st Century?

Abstract

As other professions, automotive engineering has significantly evolved in the past couple of decades and is constantly changing to meet the society needs of the 21st Century. As an example, what is today “an ordinary car”? In general, a common person using a car for his/her own needs doesn’t think at its complexity at the amount of "work" embedded. The car is simply used. By "work" we mean all the activities involved for producing the car: multi- inter- cross disciplinary works, thus, a very complex activity. Moreover, nowadays, the rhythm of technical changes happening in the industry appears to exceed the possibilities of many educational institutions to cope with. In this context, we can say the whole educational system is challenged to produce graduate engineers “fit for purpose” as any educational institution has to take the necessary actions to close the existing gap between the industry needs for multi-skilled engineers and the current supply of graduate engineers. As thus, the paper will deal with the design of the automotive engineering curriculum in relation to: – what kind of mathematics should be taught to automotive students? – how can mathematics should be taught prior to higher education so that to be more efficient in the university? – how can be achieved an optimal integration of the math contents with those of the thermodynamics, gas dynamics, vehicle dynamics, etc? – how can teaching and learning of mathematical contents can be linked to the students' engineering tasks for their achievements? Hence the rhetorical question of our study.

Keywords: Mathematics educationengineering educationprofessional competence

Introduction

It is no doubt that the engineering is one of the oldest professions that has led to the consolidation and development of human society for whose definition today, we should start a far too complex epistemological debate, which does not help us in any way. Among the greatest unanimously recognized engineers, we find Archimedes, Leonardo da Vinci, Nikola Tesla, Gustave Eiffel, Bill Nye, Neil Armstrong, and many other, each of them at that time changed well the well-being of the society in which they lived, and also led to developing the knowledge of mankind (UNESCO, 2010, para 4). Usually, the engineer can be defined as the person who solves a major or essential problem in any field of socio-economic activities demanded by society. The "product" of such engineer's activity is based on mathematics and scientific knowledge already held, but sometimes it can lead to their development implicitly. However, it’s not only about this. Using a metaphor belonging to the famous Nigerian novelist Adichie (2009), too often, solving problems it’s engineer’s “single story”. In an summary published on The Conversation magazine article Seepersad (2016) said that the “many young people, women and men alike, hear that story and can’t relate to it. They may be quite skilled in math and science, and they may enjoy solving problems, but they want to do much more than that. They want to be creative and collaborative. They want to design systems that make people healthier and safer and preserve the environment and make the world a better place. What they don’t hear is that engineers do all of these things. Engineers design everything – absolutely everything – in our built environment. Engineers are much more than a single story.”

We can give a lot of examples in this regard, but we only mention one already classic in the field of automotive engineering: first, it was Ford which built a “beautiful car” and it was only then that the science of “car dynamics” emerged. Engineering, like many other professions has evolved significantly in the past couple of decades and is constantly changing to meet the needs of society” (Henderson & Broadbridge, 2007, p. 4).

Nowadays, there is an intense concern to provide young engineers with the skills and knowledge to work in their profession. In this respect, the studies start from the analysis of the pupils' level of education at the high school level. It is trying to find problems at this level and solving them to provide students with minimal knowledge to prepare themselves in the field of engineering. Also, there are studies on the activity of engineering universities, if these do what they have to do, to work and train these students, if they satisfy students and industry expectations. In England, national STEM (science, technology, engineering and mathematics) Programme promotes the importance of design & technology and its relationship with mathematics and sciences in the secondary school. Regarding the usefulness of mathematics, Barlex (2009) shows the potential of cross-curricular links between design & technology, mathematics and science. Already in the UK there are programs that support teachers in curriculum correlation in order to make pupils understand the design and technology with mathematics help. In his study, Barlex (2009) claims that a way to improve the teachers’ activity consists in working with science teachers to develop schemes of work in which pupils use scientific knowledge and understand how to support the authentic design decisions they make. In Australia, The Carrick Institute for Learning and Teaching has funded a project to examine mathematics for 21st century engineering students (Henderson, 2007). In their study one question was: “Have there been changes to the academic backgrounds of students entering engineering degree programs?”. In this subject, most universities stated a decline in mathematical preparation, maybe, because of the lowering of entry standards to engineering degree programs. They claim that the majority of universities have removed the higher-level high school mathematics prerequisite. Many universities offer alternative entry routes and, generally, these students were also identified as less mathematically able. A particular concern was also expressed about changes to the high school mathematics especially about the standards at this educational level (Henderson, 2007). In order to mitigate the consequences of decrease in mathematical preparation, many Australian universities offer intensive three to four weeks courses which run before semester one of first year. Mathematics subject content for engineering students has become less demanding with many courses containing remedial aspects (Nicolescu & Macarie, 2012).

In order to know how could enhance a sustainable world-class higher education engineering sector that meets the graduate recruitment needs of industry, the Royal Academy of Engineering’s Educating engineers for the 21st century (EE21C) examined the needs of industry in depth. Their report examines the drivers for change behind the development of ‘experience-led degrees’ that aim to equip students with the employability skills needed by industry (Arlett, Lamb, Dales, Willis, & Hurdle, 2010). This report provides examples of mechanisms that enable academics to gain insight into industry. They have to collaborate with engineers in industry on the development of the experienced teaching components. They claim that it is very important that the engineers from industry come into universities to support teaching (Arlett, 2010).

A few institutions stated in The Carrick Institute for Learning and Teaching project (Henderson, 2007) that mathematical and statistical content has been reduced in response to industry requirement for engineering students to learn increased soft skills.

The engineering student body increased in the overall proportion of the population attending university, increased in the number of international students and, increased the number of students in paid employment. Also, over the past few years there has been an increase in the number and proportion of women in engineering domain (Henderson, 2007).

In this context, the engineering curriculum has to adapt to provide students with an adequate foundation to enter the profession. Some authors (Henderson, 2007) claim also, that the learning achievements are greater in case of active learning, meaning “learning by doing” rather than the traditional lecture format. On this matter, in one of our past works, we discussed the “project-based learning” techniques (Clenci, Niculescu, & Zaharia, 2016).

It is crucial to address the increased student variability and to consider differing learning styles. Easily accessible student support systems are also key to an effective engineering mathematics subject (Henderson, 2007).

An increased emphasis is on heuristic ideas using engineering problems in mathematics tutorial classes, rather than mathematical rigour, also and greater use of software. Students are now able to access most subject and support material from online platforms, also video problem solutions are available online (Henderson, 2007).

Henderson in his study (2007) claims that mathematics comprises 25% of first year study and is identified as a crucial enabling skill for engineers to conduct technical work, nevertheless it was agreed that some of the abstract content would be removed. Most commonly, engineering staff develops a list of key topics after which mathematics develop a curriculum around these guidelines. Mathematics is taught to engineering students in small groups (20-30 students in a class). Teachers feel that students are more engaged in the foundation mathematics courses than they have been in previous years and the collaboration between the departments in designing the engineering problems is very important. Software such as WeLearn and CalMath appear to be effective in providing additional practice with feedback for students (Henderson, 2007).

The above considerations were given to emphasize the complexity of engineering education in general, and in particular, of mathematics education for world-class higher education engineering sector that meets the graduate recruitment needs of industry.

In the following, it is presented a study generated by our preoccupations to improve the mathematics education for automotive and transport engineering students in the University of Pitesti.

Problem Statement

This study is particularly focused on Automotive and Transport Engineering domain. Its academic curriculum features the following courses on superior mathematics: “Linear Algebra, Analytical and Differential Geometry”, developed in the first semester of study with 56 hours of direct didactic activity, “Calculus or Mathematical Analysis”, developed in the first two semesters with 98 hours of direct didactic activity and “Special Mathematics” in the third semester with 42 hours of direct didactic activity. More or less, this is the current status in Romania for the higher education in the Automotive Engineering field (by summing up, approximatively 200 hours of direct didactic activity in superior mathematics). Obviously, these courses are present in the academic curriculum simply to serve the downstream disciplines. However, we believe being simply present in the academic curriculum is not enough for a real usefulness of this superior mathematics. That's why, we wonder if at the end of the mathematics training course, our students are able to easily navigate, for instance, a classical course of Automotive Dynamics such as of Jazar (2008) or Rajamani (2006). The responsibilities of curriculum design for engineers also come to math teachers employed on such an educational project, meaning that they have to consider math content approaches to future learning needs of students' engineering disciplines, not only to the mathematics theories. Among the many examples that we could bring into debates in these issues of connection and harmonizing the content of mathematics courses with engineering sciences courses, we focus on two of them. The first is related to the theory of differential equations which have to approach specific equations linked for example with the car's motion equations, with the car's vibrations, etc. The second example is related to the content taught in the course of analytical and differential geometry, which has an arguable finality related to the geometric description of objects of engineering interest such as road surfaces (roads, roads, highways, etc.), the car's surface, the surface of the cavitating flow, etc. In fact, these important issues seem to be details in a training program for engineers, but this have an essential role in the holistic of the professional personality of an engineer.

This being the context, following a questionnaire addressed to our students and graduates an idea emerged: an important part of our students and graduates seem not only not having the necessary superior mathematics skills but they are not even convinced about the usefulness of having these disciplines in the academic curriculum. Therefore, some questions need to be clearly specified for both teachers and students, as seen below.

Research Questions

Three ideas need to be carefully taken into consideration in order to meet the target of real usefulness of this superior mathematics:

• The selection of the mathematical notions to be taught must be a consequence of a real dialogue with the teachers from downstream who may as well be called beneficiaries, i.e., nothing should be taught for the sake/love of the art but having in mind the following idea: to whom it may really be useful?

• These selected notions of superior mathematics which are taught have to be really used in a great extent in the downstream disciplines (the teachers from these disciplines to really act like beneficiaries); the greater the extent the better for the perceiving of the usefulness of this superior mathematics

• Last but not least, being about abstract and complex notions, the teaching method is of paramount importance.

The ones doing the class of (superior) mathematics are often persons with a great ability of perceiving complex and pure abstract notions. They are able to play with really complex mathematical operators/theorems/formulations and to perceive complex senses. But let’s not forget that in an engineering curriculum, it’s about applied mathematics, i.e., the kind of mathematics which serves the physical world an engineer is dealing with. In other words, the ones in charge of the superior mathematics should themselves learn the technique of communication of these abstract and complex notions. Thus, their challenge is how to transmit these complex notions in a comprehensible manner for the majority of the engineering students. The main task of a mathematician teacher is to mediate between the great minds of mathematics and the broad public of still teenage engineering students. It’s what we may call the engaged mathematician teacher who should try to avoid using an inapproachable language. We think everybody easily agree with this idea; however, despite this, not everybody apply it. In other words, a real danger for the teacher of mathematics, which is more connected with the psychology of the human being is to avoid being drawn into the need to kind of showing off, i.e., to publicly exhibit or display a kind of hermetic speech that no one understands “for what could be more respectably than the things which are hard to be understood” (Liiceanu, 2005, p. 12)? But how many of us the teachers (now, we extend the addressability) recognize that sometimes we get pleasure by adopting such a behaviour as to make an impression? Probably, nobody. Nevertheless, what is the main task of any teacher? Sometimes, to put it very simple, as well, to do his/her best to make students to understand. To reach this simple purpose, the teacher needs to go down amongst the students and to make them understand by adapting the language and choosing the right communication means. As Liiceanu (2005) said about philosophers, the mathematics courses as well are not to be as the religious service spoken in Latin that few understood but many feared.

So, by resuming, on the one hand, it’s about carefully selecting the content having always in mind the need for showing/proving the usefulness of the notions taught and, on the other hand, it’s about the teaching method (as always).

If everything were well on this matter then perhaps this study would not have been amongst our preoccupations. But we do not think it is the case. So, when did the question which gives the title of our article appear in our preoccupations? Our perception as teachers involved in the academic curriculum of Automotive and Transport Engineering was first confirmed by the answers to our annually surveys of some of our best graduates currently well absorbed in some world-renowned industrial companies in our field. Sadly, they believe this superior mathematics isn’t necessary anymore. Of course, not every job/occupation from the labour market needs a decent competence in superior mathematics. However, when we discuss about R&D, then we think this should be an important prerequisite. Hence, this claim of some of our best graduates triggered this study.

Purpose of the Study

The purpose of this study is, to a large extent, similar to that in Kent & Noss (2003), but carried out for students of Automotive and Transport Engineering at the University of Pitesti. The survey conducted on the basis of the questionnaire given to our students led to some conclusions that are important both for the design of mathematical and engineering curriculum contents, and for the teaching of teachers in relation to the students from this engineering faculty. This study was conducted primarily to provide an objective argumentation for the changes that we have to make together, mathematics teachers and teachers teaching engineering courses so that our students acquire professional skills appropriate to the expectations and needs of the future employers.

Research Methods

As mentioned before, in our endeavour we relied on a questionnaire applied to the automotive engineering bachelor students and graduates.

The following questions were formulated:

• how would you appreciate the usefulness of mathematics disciplines for the training of engineer;

• to what extent do you consider that in order to meet the disciplines of superior mathematics, a good knowledge of high school mathematics disciplines is necessary?

• to what extent you can appreciate the degree to which the teachers of superior mathematics disciplines have specified explicit links or have provided examples with specific references with subsequent or downstream specialized/engineering disciplines?

• to what extent do you consider that the content of superior mathematics disciplines has been combined with the expectations of employers in the automotive engineering fields (as you know them or you can imagine)?

• regarding the teaching method, to what extent do you think it has been adapted?

Findings

The questionnaire was answered by 231 students out of a total of 492 students from Automotive and Transport Engineering bachelor degree from University of Pitești.

A graphic interpretation of the results is given in figures below.

See Full Size >

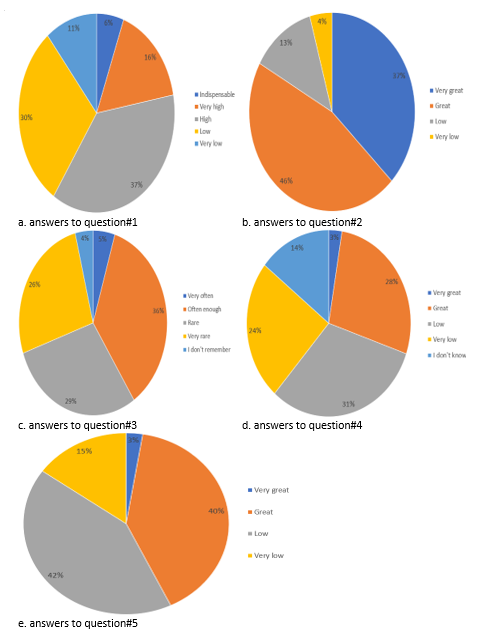
Subsequently, the answers are commented in a brief manner:

• 41% of the respondents consider the usefulness of the superior mathematics for the training of engineer is arguable (fig. 1, a )

• 83% of the respondents think that the good understanding of superior mathematics is conditioned by a good knowledge of high school mathematics (fig. 1, b )

• unfortunately, 59% of the respondents consider that the teachers of superior mathematics disciplines haven’t specified enough explicit links or provided enough examples with specific references with subsequent or downstream specialized/engineering disciplines (fig. 1, c )

• it’s also a pity that 69% of the respondents think the content of superior mathematics disciplines hasn’t been combined properly with the expectations of employers in the automotive and transport engineering fields (fig. 1, d )

• regarding the teaching methods, 57% of the respondents consider that they haven’t been really adequate (figure 1 , e ).

Further to this survey, we dare to conclude that some reflexions in the teachers’ mind are necessary: for instance, reconsideration of the teaching method and selection of the content according to the specific needs in the downstream engineering disciplines. The latter means an efficient dialogue and contact with the teachers of engineering disciplines, which, obviously isn’t only the responsibility of the mathematicians. It’s a two-way action, meaning that the “beneficiary” (i.e., engineering teacher) should as well come towards the mathematicians in order to provide the engineering problem which needs a specific mathematical formulation.

Conclusion

In general, we think the findings of our study are the same as the ones of other authors who published articles on the same subject: which is the adequate mathematics for the education of the engineers in the 21^st century? Certainly, these findings are general truths connected to the reality of mathematics education nowadays for engineering students (in our case). For instance, we quote some ideas which we think best describe this subject: „1. It is time to reconsider pedagogical approaches that can best „deliver” the mathematical needs of students. Mathematics could benefit from being more „pulled” into the context of design-oriented engineering teaching, rather than „pushed” into students in the absence of a context. This entails a shift in approach from teaching mathematical techniques towards teaching through modelling and problem solving; 2. Carefully-designed IT use can make it possible to use mathematical ideas before understanding the techniques. In the pre-computational era, a strong objection to pull-based mathematics was that to use a mathematical idea properly required a detailed understanding of the techniques of its application. But times, and technologies, change; 3. There is a need for national leadership to stimulate, and to promote the spread of, the innovative work in curriculum design and delivery currently being carried out by enthusiastic individuals and individual departments. This is a role that the professional institutions (together with cross-sector engineering organisations such as the Engineering Technology Board) should be well placed to assume, as campaigners for the engineering profession and controllers of the accreditation mechanisms for engineering degrees” (Kent & Noss, 2003, p. 5). But, beyond these, we have some conclusions that are specific to the Romanian engineering education. Thus, as everywhere, our students' attitude towards mathematics is also related to their knowledge acquired in high school, especially as many of them are graduates of technological and / or vocational high schools. Even if the students come from theoretical high schools, their mathematical competences are in line with the quality standards established after the reform implemented in the secondary education, especially after the Bologna Treaty. Unfortunately, in Romania, it is not possible to implement the preparatory classes needed to supply to the fresh students a minimal level needed to attend math courses at engineering faculties. On the other hand, this vulnerability of some students to math courses sometimes makes them "victims" for some of the teachers who do not respect the ethical and moral standards of academic rank. Last but not least, this situation is also an argument for engineering teachers to lower the standard of their specialized courses. "Because students do not know mathematics, we must avoid the formalism of mathematics in the content of these courses. "What can we do to correct this situation? The answer to this question is surely not about what kind of mathematics is needed for engineer education in the 21st century. Mathematics and engineering have always been inseparable, and they evolve naturally together. Nevertheless, even though the mathematics teaching for engineering education is a complex subject not meant to be solved out easily, it’s our belief that many improvements are up to the teachers’ will to make things better.

Acknowledgments

The authors of this paper would like to express their gratitude to the students who were kind enough to answer the questionnaire mentioned before. Certainly, they understood it’s about a feedback the school needs to improve its performance.

References

1. Adichie, C.N. (2009). The danger of a single story. Retrieved form https://www.ted.com/talks/chimamanda_adichie_the_danger_of_a_single_story
2. Arlett, C., Lamb, F., Dales, R., Willis, L., & Hurdle, E. (2010). Meeting the needs of industry: the drivers for change in engineering education. Engineering Education, 5, 18-25. DOI: 10.11120/ened.2010.05020018
3. Barlex, D. (2009). The STEM Programme in England – help or hindrance for design & technology education? Retrieved from https://www.iteea.org/File.aspx?id=86937&v=a0b1a6e7.
4. Clenci, A., Niculescu R., & Zaharia, C. (2016). On the education of the automotive engineer through project-based approach, EduWorld 2016, 7th International Conference: Vol. XXIII. Education facing contemporary World Issues (pp. 1289-1287). DOI:
5. Henderson, S., & Broadbridge, P. (2007). Mathematics for 21st Century Engineering Students. In H. Søndergaard& R Hadgraft (Eds.) Proceedings of the 18th Conference of the Australasian Association for Engineering Education, (pp. 1-8). Melbourne: Department of Computer Science and Software Engineering, The university of Melbourne. Retrieved from https://trove.nla.gov.au/work/153068532?q&versionId=217772889
6. Jazar, R. N. (2008). Vehicle Dynamics: Theory and Applications. New York: Springer.
7. Kent, P., & Noss, R. (2003). Mathematics in the University Education of Engineers. A Report to the Ove Arup Foundation. London: The Ove Arup Foundation. Retrieved from http://discovery.ucl.ac.uk/10001300/
8. Liiceanu, G. (2005). Cearta cu filosofia [Quarrel with philosophy]. București: Humanitas.
9. Nicolescu, B.N., & Macarie, T. (2012). About the role of the mathematics in the engineering education. In C. Oprean, N. Grünwald & C.V. Kifor (Eds.), International Conference on Engineering & Business Education, Innovation and Entrepreneurship: Conference Proceedings, Progress by Exchange. Cultural Innovation and Educational Development (pp. 373-376). Sibiu: Lucian Blaga University. Retrievedfromhttp://www.icebe.net/fileadmin/user_upload/Downloads/2012/proceedings_2012__1_.pdf
10. Rajamani, R. (2006). Vehicle Dynamics and Control. New York: Springer.
11. Seepersad, C. C. (2016). How to involve more women and girls in engineering. U. S. News & World report. Retrieved from http://theconversation.com/how-to-involve-more-women-and-girls-in-engineering-55794
12. UNESCO. (2010). Engineering: Issues Challenges and Opportunities for Development. Paris: UNESCO Publishing. Retrieved from https://unesdoc.unesco.org/ark:/48223/pf0000189753