Abstract
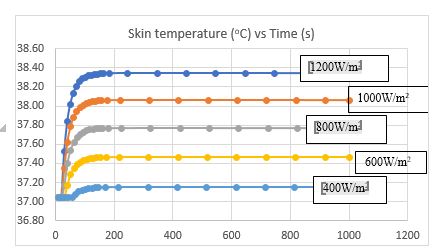
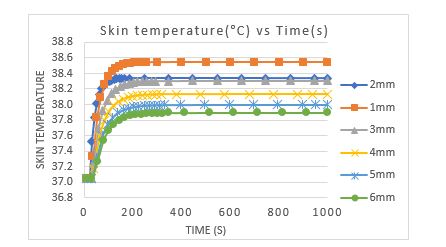
Firefighting is a life-threatening situation, they are exposed to extreme heat fire and explosion. Burn injury is the most common injury occur in firefighting. The firefighters are enforced to used personal protective clothing to protect them against fire. The purpose of the study is to assess the effectiveness of fire fighter’s personal protective clothing by utilizing heat transfer model in finite element analysis. The model applied bioheat equation to solve heat transfer through living tissue at muscle area with consideration of metabolic heat generation and blood profusion. The validation of the heat transfer model was performed by comparing the predicted and measured skin temperatures with an acceptable error of less than 20%. The study found the skin temperature increases significantly with the heat flux intensities. The heat flux of 1200W/m2 causes to skin temperature 38.3°C. Skin temperature will gradually rise at t = 0 second and approaches it’s steady at t =198 seconds. The maximum air gap thickness reduces the heat stress effect. The reduction of 1 mm air gap thickness contributes to an increment of 0.2°C of the skin temperature.
Keywords: “Fire Fighter”“Heat Stress”; “Bioheat”; “Heat Transfer”; “Heat Stress”
Introduction
Thermal protective clothing is primarily designed to provide protection from thermal hazards which include exposure to high temperature radiant sources, flame impingement, hot liquids and gasses. It is difficult to completely define the nature and characteristics of these thermal hazards, because of the many environmental and physical factors involved. Thermal hazards can be quantified through heat transfer analysis. Heat transfer from the thermal hazards can be transmitted by radiation, convection or conduction, or a combination of all. Heat flux transmitted by thermal hazards ranges from 20 – 160 kW/m2 and can be encountered during large fires and explosions (He, Park, Li, & Kim, 2017). Severe thermal problems and life threatening injuries are associated with these conditions. For the existing protective clothing, the tolerance time for people that can sustain such heat flux intensities is in the range of 5 to 20 seconds (Barr, Gregson, & Reilly, 2010).
Approximately 100 firefighters suffer from fatal injuries in the USA annually and over 30,000 firefighters are subject to injuries while firefighting (Karter, 2012). From 2007 to 2012, firefighters who suffered from skin burn injuries received them most frequently in the head area (38%), the arm or hand (30%), the neck or shoulder area (16%), and the leg or foot (8%) (Karter, 2012). It is shown from the etiology of injuries to firefighters that scald burns were responsible for injury (65%) and flame burns caused injury to 20% of firefighters. However, other 15% patients received contact or compression burns (Kahn, Patel, Lentz, & Bell, 2012).
Quantifying the burn injury from firefighters during firefighting is impossible. Since there are many factors, influence the burn injuries such as heat flux, protective clothing material properties, metabolic rate and blood profusion rate. However, it could be achieved if the temperature of human skin was obtained. The temperature of the human skin can be determined through the Pennes bioheat equation (Pennes, 1948). Blood profusion, metabolic rates and skin tissue layers control the human skin temperature by heat transfer through the human skin's tissue.
Air gap thickness has strong influence to the skin burn. The air gaps that located between human skin and the inner surface of the personal protective clothing developed a buffer region resulting restricted heat transfer from the heat exposure to the human skin. When exposed to the heat, the air gap become an insulator protecting from burn injuries. It provides thermal insulation limits heat transfers to the human skin. A human body scanner was used to study the effect of air gap thickness with thermal manikin (Li, Zhang, & Wang, 2013; Psikuta, Frackiewicz-Kaczmarek, Frydrych, & Rossi, 2012). However, these experiments require complex equipment and exhaustive procedure.
Problem Statement
The clothing evaluation for the material was done by using experimental and mathematical model. The experimental consist of three methods known as bench scale test (Song, Cao, & Gholamreza, 2011), thermal manikin test (Barr et al., 2010; Bröde et al., 2008; Fu, Yuan, & Weng, 2015; Havenith et al., 2006; Havenith et al., 2005) and test method for wet sample (Barker, Guerth-Schacher, Grimes, & Hamouda, 2006; Keiser & Rossi, 2008; Wakatsuki, Morii, Ogawa, & Tsuji, 2013; F. Zhu & Li, 2011; F. L. Zhu & Zhou, 2013). There were many types of sensors had been developed to simulate the human body specially to predict the amount of heat transferred through the human bodies during fire exposures. The thermal sensors available are TPP/RPP sensor, embedded sensor, skin simulant sensor, PyroCal sensor and water cooled sensor. These sensors commonly used for the thermal protective clothing evaluation (Barker et al., 2006; Sipe, 2004) sensors were embedded to record the amount heat transfer through clothing layer from the heat source. However, all type of sensors were conducted with fixed skin temperature. It is differ with real human skin temperature. During physical activities, core temperature is proportional to the metabolic rate and dependent of the wide range of environment conditions such as ambient temperature and humidity. The skin temperature is depends on skin blood profusion and the environment conditions (Fontana et al., 2017; Kenefick, Cheuvront, & Sawka, 2007). Strenuous physical activities such as running could cause fluctuations in skin temperature (Gan, Cheng, Ding, & Pan, 2010). The blood flow depends on fiber type and moisture level (Tanda, 2016). Therefore, there is a need to imitate the physiology human skin reaction to the environment.
Research Questions
How to predict firefighter’s skin temperature with the variation of heat fluxes and the air gap thicknesses?
Purpose of The Study
This study is a new and practical approach to predict skin temperature by applying the (Pennes, 1948) bioheat equation and finite element analysis. It could lead more accurate model for the evaluation personal protective clothing evaluation. There are many researchers (Chitrphiromsri & Kuznetsov, 2005; Ghazy & Bergstrom, 2011; Onofrei et al., 2015) used bioheat as it is relevant for determination of the skin temperature. The equation takes into consideration the human metabolic rate, the skin material properties, the blood profusion rate. These variables are depending with the human physical activities that could lead to rise on the metabolic heat generation and the human skin temperature. The equation can avoid from using human subject in the climatic chamber which is dangerous and against the principal of humanity.
Research Methods
The analysis begins with solving the bioheat equation which is merely a steady conduction heat transfer of living tissue. The equation solves heat transfer at muscle layer to determine the temperature between skin layers and muscle which in turn this temperature was used as a boundary condition in the finite element analysis. The ANSYS software version 14 was used as a tool to perform the finite element analysis under transient conditions.
Mathematical Model
Pennes (1948) introduced a modification of heat transfer in living tissue phenomena by adding metabolic heat generation and the heat exchange of thermal energy of flowing blood and the surrounding tissue. Both factors can be identified as the heat sources of heat in the heat transfer equation as the following:
(1)
Where and is the metabolic and profusion heat rates. While the thermal conductivity k is assumes to be constant.
(2)
Equation 2 represents the heat transfer rate of the blood flowing in the small capillaries. The inlet (arterial temperature) and exit temperatures of the blood are denoted as Ta and T, respectively. The rate at which the skin tissue layer gains the heat is the rate at which the blood loses the heat. The blood profusion rate is denoted as w (m3/s of the volumetric blood flow) while
and
are the blood density and specific heat respectively.Consider a human body that has a muscle thickness, Lm=34.2mm and a skin fat thickness, Lsf of 12.08mm (Ogaswara, 2012) as illustrated in the Figure
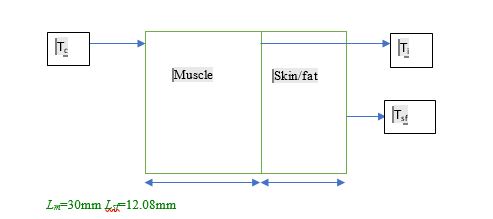
The rate of heat transfer between the skin and the adjacent air can be described as:
(3)
Where the total resistance,
The radiation,
The excess temperature at the boundary given by (Bergman, Incropera, DeWitt, & Lavine, 2011)are;
(4)
(5)
The prescribed temperature involving two boundary conditions given by (Bergman et al., 2011)is;
(6)
The heat leaving the muscle equal heat transfer through the skin/fat. The heat transfer rate at
(7)
Combining the equation 3 and 7 will solve the surface temperature at muscle
(8)
Where
The skin/fat temperature
Therefore the skin temperature is
(9)
Finite Element Model
A simplified two-dimensional model of multi-layer clothing materials was developed using ANSYS transient thermal finite element software as shown in Figure
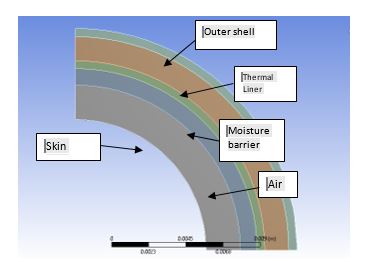
Figure
Findings
The model developed by (Onofrei et al., 2015) was based on numerical analysis for solving a heat transfer model of the protective clothing exposed to heat. The goal of the study is to evaluate the thermal performance of multi-layer materials when they are exposed to the heat hazard. She modelled the multi-layer materials system as a rectangle geometry which employed a two-dimensional quarter circle geometry. When compared to the (Onofrei et al., 2015) model, the model presented in this paper used finite element analysis to solve the heat transfer problem through the protective clothing layers on the hand and leg sections of human body. The model in this study are in two-dimensional cylindrical geometry. However both studies used the bioheat equation of the living tissue to solve the heat transfer problem. Table
Table
Figure
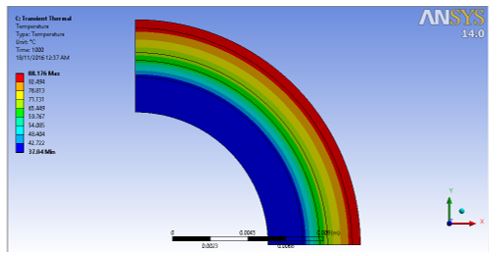
Figure
Figure
Conclusion
Quantifying heat intensity in the real firefighting condition to protective clothing for firefighters is complex. Life-threatening environment during actual firefighting condition test and the size of the attire are the contributory factors of the complexity. The goal of this study is to evaluate the effects of heat intensity and air gap of a multi-layer material on the skin burn temperature. The finite element analysis is used for solving the heat transfer problem through the clothing layer. It is found that the skin temperature increases significantly with the heat flux intensities. The heat flux of 1200 W/m2 causes the skin temperature to reach 38.3ºC. The reduction of 1 mm air gap thickness contributes to an increment of 0.2ºC of the skin temperature. As the air gap thickens, less heat is transmitted to the skin surface. It is also noticed that the material properties of firefighters protective clothing are a causative factor for minimizing burn injury to the skin. Especially to the material that holds low thermal conductivity and heat capacity.
Acknowledgments
This research work is supported by Geran Universiti Penyelidikan (GUP) QJ130000.2524.18H79 provided by Universiti Teknologi Malaysia (UTM).
References
- ASHRAE. (2001). Fundamentals. American Society of Heating, Refrigerating and Air Conditioning Engineers, Atlanta, 111.
- Barker, R. L., Guerth-Schacher, C., Grimes, R. V., & Hamouda, H. (2006). Effects of Moisture on the Thermal Protective Performance of Firefighter Protective Clothing in Low-level Radiant Heat Exposures. Textile Research Journal, 76(1), 27-31. doi:
- Barr, D., Gregson, W., & Reilly, T. (2010). The thermal ergonomics of firefighting reviewed. Appl Ergon, 41(1), 161-172. doi:
- Bergman, T. L., Incropera, F. P., DeWitt, D. P., & Lavine, A. S. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons.
- Bröde, P., Havenith, G., Wang, X., Candas, V., Den Hartog, E. A., Griefahn, B., . . . Nocker, W. (2008). Non-evaporative effects of a wet mid layer on heat transfer through protective clothing. European journal of applied physiology, 104(2), 341-349.
- Chitrphiromsri, P., & Kuznetsov, A. V. (2005). Modeling heat and moisture transport in firefighter protective clothing during flash fire exposure. Heat and mass transfer, 41(3), 206-215.
- Cooper, T., & Trezek, G. (1971). Correlation of thermal properties of some human tissue with water content. Aerospace medicine, 42(1), 24-27.
- Fiala, D., Havenith, G., Bröde, P., Kampmann, B., & Jendritzky, G. (2012). UTCI-Fiala multi-node model of human heat transfer and temperature regulation. International journal of biometeorology, 56(3), 429-441.
- Fontana, P., Saiani, F., Grütter, M., Croset, J.-P., Capt, A., Camenzind, M., . . . Annaheim, S. (2017). Exercise intensity dependent relevance of protective textile properties for human thermo-physiology. Textile Research Journal, 87(12), 1425-1434.
- Fu, M., Yuan, M., & Weng, W. (2015). Modeling of heat and moisture transfer within firefighter protective clothing with the moisture absorption of thermal radiation. International Journal of Thermal Sciences, 96, 201-210.
- Gan, Y., Cheng, L., Ding, X., & Pan, N. (2010). Blood flow fluctuation underneath human forearm skin caused by local thermal stimuli of different fabrics. Journal of Thermal Biology, 35(7), 372-377.
- Ghazy, A., & Bergstrom, D. J. (2011). Influence of the air gap between protective clothing and skin on clothing performance during flash fire exposure. Heat and mass transfer, 47(10), 1275-1288.
- Havenith, G., HolmÈr, I., Meinander, H., denHartog, E., Richards, M., Brˆde, P., & Candas, V. (2006). Assessment of thermal properties of of protective clothing and their use. EU Final Report.
- Havenith, G., Wang, X., den Hartog, E. A., Griefahn, B., Holmer, I., Meinander, H., & Richards, M. (2005). Interaction effects of radiation and convection measured by a thermal manikin wearing protective clothing with different radiant properties.
- He, J., Park, E., Li, J., & Kim, E. (2017). Physiological and psychological responses while wearing firefighters’ protective clothing under various ambient conditions. Textile Research Journal, 87(8), 929-944.
- ISO, E. (2002). 6942-2002 Protective clothing-protection against heat and fire——Method of test: Evaluation of materials and material assemblies when exposed to a source of radiant heat. In: Brussels: European Committee for Standardization.
- Kahn, S. A., Patel, J. H., Lentz, C. W., & Bell, D. E. (2012). Firefighter burn injuries: predictable patterns influenced by turnout gear. Journal of burn care & research, 33(1), 152-156.
- Karter, M. J. (2012). Patterns of firefighter fireground injuries: National Fire Protection Association Quincy, MA.
- Keiser, C., & Rossi, R. M. (2008). Temperature analysis for the prediction of steam formation and transfer in multilayer thermal protective clothing at low level thermal radiation. Textile Research Journal, 78(11), 1025-1035.
- Kenefick, R. W., Cheuvront, S. N., & Sawka, M. N. (2007). Thermoregulatory function during the marathon. Sports medicine, 37(4-5), 312-315.
- Li, J., Zhang, Z., & Wang, Y. (2013). The relationship between air gap sizes and clothing heat transfer performance. The Journal of The Textile Institute, 104(12), 1327-1336.
- Onofrei, E., Petrusic, S., Bedek, G., Dupont, D., Soulat, D., & Codau, T.-C. (2015). Study of heat transfer through multilayer protective clothing at low-level thermal radiation. Journal of Industrial Textiles, 45(2), 222-238.
- Pennes, H. H. (1948). Analysis of tissue and arterial blood temperatures in the resting human forearm. Journal of applied physiology, 1(2), 93-122.
- Psikuta, A., Frackiewicz-Kaczmarek, J., Frydrych, I., & Rossi, R. (2012). Quantitative evaluation of air gap thickness and contact area between body and garment. Textile Research Journal, 82(14), 1405-1413.
- Sipe, J. E. (2004). Development of an instrumented dynamic mannequin test to rate the thermal protection provided by protective clothing. MSc Thesis, Worcester Polytechnic Institute,
- Song, G., Barker, R. L., Hamouda, H., Kuznetsov, A. V., Chitrphiromsri, P., & Grimes, R. V. (2004). Modeling the thermal protective performance of heat resistant garments in flash fire exposures. Textile Research Journal, 74(12), 1033-1040.
- Song, G., Cao, W., & Gholamreza, F. (2011). Analyzing stored thermal energy and thermal protective performance of clothing. Textile Research Journal, 81(11), 1124-1138.
- Tanda, G. (2016). Skin temperature measurements by infrared thermography during running exercise. Experimental Thermal and Fluid Science, 71, 103-113.
- Wakatsuki, K., Morii, N., Ogawa, Y., & Tsuji, H. (2013). Influence on Skin Burns by Water Absorbed Station Wear and Underwear in Firefighter Clothing. Paper presented at the Advanced Materials Research.
- Weaver, J. A., & Stoll, A. M. (1967). Mathematical model of skin exposed to thermal radiation. Retrieved from
- Zhu, F., & Li, K. (2011). Numerical modeling of heat and moisture through wet cotton fabric using the method of chemical thermodynamic law under simulated fire. Fire technology, 47(3), 801-819.
- Zhu, F. L., & Zhou, Y. (2013). Modelling heat-moisture transport through firefighters’ protective fabrics from an impinging flame jet by simulating the drying process. Fibres & Textiles in Eastern Europe.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
17 May 2019
Article Doi
eBook ISBN
978-1-80296-061-7
Publisher
Future Academy
Volume
62
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-539
Subjects
Business, innovation, sustainability, environment, green business, environmental issues
Cite this article as:
Kamsah, N., Mohamed Kamar, H., Md Tap, M., & Zainol*, Z. N. (2019). Application Bioheat Equation For Heat Transfer Model Of Firefighter’s Burn Injury. In M. Imran Qureshi (Ed.), Technology & Society: A Multidisciplinary Pathway for Sustainable Development, vol 62. European Proceedings of Social and Behavioural Sciences (pp. 164-174). Future Academy. https://doi.org/10.15405/epsbs.2019.05.02.15
