Information Limitations On Firm Growth

Abstract

The contemporary theory of the firm involves two key mechanisms for determining the firm size: contractual information asymmetry and the concept of specific assets within the theory of transaction costs. Both mechanisms are based on particular information mechanisms of firm control. The paper describes the model of loss and recovery of firm control as a key factor which determines limitations on the firm size. The model applies developments of the information theory, in particular, Ashby’s law of requisite variety. Formally loss of control is result of firm size growth due to increase of relative entropy between “decisions making” and “controlled” parts of firm. Control recovery is an education process. It needs time and output capacity of communication cannel these parts of firm. In common case we can see that the control loss process will dominate the control recovery process. The requisite variety law helps us describe a limitation mitigation mechanism and explain why the concept of an optimum firm size is useless.

Keywords: Theory of the firmfirm sizeinformation theorythe law of requisite variety

Introduction

In The Nature of the Firm, Ronald Coase argues that the theory of the firm as a part of the general economic theory should answer why firms exist, why their sizes are limited, what factors determine their market positions (Coase, 1937). The present article studies factors limiting the firm growth and preventing firms from reaching unlimited sizes.

The institutional theory developed by Coase uses the concept of transaction costs. It argues that firms grow until the efficiency of their resource distribution mechanism is higher than the efficiency of the market mechanism. The main emphasis of researchers is on the effects of market failures and causes of market efficiency reduction, which contribute to the firm growth (Williamson, 1971). The most typical market failures are transactions with ‘specific’ assets (Klein, Krawford, & Alchian, 1978) whose key feature is an increasing value after the transaction. A contractor concluding a contract with specific assets become dependent on his/her partner due to high costs of contract annulment and search for its adequate substitution in case of contract violation. It allows the partner to take advantage of his/her position, which is referred to as ‘opportunistic behavior’. Incorporation of a business partner becomes beneficial. The theory suggests that the firm growth is stimulated by external rather than internal factors. Some authors treat the principles of the theory carefully due to their direct nature (Holmström & Roberts, 1998).

The issue of principal-agent relations is a parallel branch of the theory (Jensen & Meckling, 1976). Initially, it marked an information gap between the principal (owner of investment resources) and the agent (manager, owner of information about resource usage). Information asymmetry does not allow principals to impose maximizing behavior for their benefits. Furthermore, it makes it possible to assess the efficiency of agent’s decisions (Hart, 1989). The theory of contracts generalizing the concept of agents deals with mechanisms of control and interest alignment through contracts limiting egoistic actions of the agents with regard to principal’s tasks. These researches expanded views of the firm produced by the classical theory but they do not answer the questions posed by Coase.

Oliver Hart describes the results of the fruitful theory of the firm as follows: “An outsider to the field of economics would probably take it for granted that economists have a highly developed theory of the firm. After all, firms are the engines of growth of modern capitalistic economies, and so economists must surely have fairly sophisticated views of how they behave. In fact, little could be further from the truth. Most formal models of the firm are extremely rudimentary, capable only of portraying hypothetical firms that bear little relation to the complex organizations we see in the world.” (Hart, 1989, p. 1757). As a result, economists gained some insight into internal processes of the firm and its environment, which is not supported by realistic formal models.

Problem Statement

Further researches focused on empirical studies of the effects determining the firm growth using econometric methods. They showed that the firm growth is restricted by financial, legal and corruption challenges (Beck, Demirgüç-Kunt, & Maksimovic, 2005), the strong legal system is a key factor while the financial and industrial development is a secondary one (Kumar, Rajan, & Zingales, 1999), the firm growth increases salary gaps between large and small firms (Fox, 2009). The research on loss effects for economies of scale (Canbäck, Samouel, & Price, 2006) proved five key hypotheses: (I) bureaucratization, motive loss and communication errors increase with the firm growth; (II) large firms demonstrate economies of scale; (III) loss of economies of scale affects the production volume of the firm; (IV) economies of scale make large firms more lucrative than small ones; (V) loss of economies of scale is mitigated by transaction cost factors: organization structure and integration for using specific assets.

Research Questions

In The Nature of the Firm, Coase said that the issue of the firm size is not about contractual relations. The causes of the firm growth cannot be identified based on the neoclassical theory and concept of economies of scale. The solution is in control procedures as far as whatever improves control techniques contributes to the firm growth (Coase, 1937). Loss of control and an increase in firm control complexity are well observed empirical facts, which seem self-evident: “There is a great deal of evidence that almost all organizational structures tend to produce false images in the decision-maker and that the larger and more authoritarian the organization, the better the chance that its top decision- makers will be operating in purely imaginary worlds” (Williamson, 1967, p. 123). For that reason, studies on hierarchical management assume that low levels are subject to only some control effects.

Purpose of Study

Theoretical issues of firm control are closely connected with the role of information systems formulated as the Solow paradox: “You can see the computer age everywhere and in the productivity statistics”. The studies on assessment issues of information systems efficiency identified a number of their sources (Brynjolfsson, 1993): objective complexity of measurements, time lags, unequal distribution of effects, and proneness of managers to make trendy decisions. However, general conclusions tell about unexpected complexity of the problem and lack of adequate tools for its solution. Successful business experience of IT mastering continued to conflict with key conclusions of the researchers and it demanded explanation (Triplett, 1999). Finally, it was agreed that the Solow paradox died. However, new highly authoritative researchers equipped with powerful econometric tools and rich body of data argue that there are no significant marks of IT investment effects on productivity increase (Acemoglu, Dorn, Hanson, & Price, 2014).

The present article aims to describe the mechanism of controllability decrease and show its relation with the firm growth. To this end, control is referred to as an activity aimed to transform a variety of states of the firm as a control object decreasing its diversity. The model explains why implementation of information systems instead of control cost reduction increases costs and improves management. Besides, it was found that the issue is closely connected with an idea of rational human behavior, which was used as a requirement for applying mathematical tools. Use of theoretical and information models became one of new research areas (Matejka & McKay, 2014). It shows that well-known tools have not exhausted their potential.

The number of workers will be used as a characteristic of the firm size. Although in rating reports, firms are located by capitalization indices, profit values and asset sizes, in special econometric studies dealing with firm sizes, the number of workers is considered as the most adequate index (Axtell, 2001).

Let us analyze a firm having K workers. At a certain point of time, one worker can perform a certain function from a limited set $n_i$, $i=\mathrm{1},...,K$. Then the total of all possible simultaneous combinations of actions consisting of $n_{\mathrm{1}}{n}_{\mathrm{2}}...n_K$elements will be referred to as set F of the firm states. Hereafter, the number of degrees of freedom will be $n_i=n$, and set $\mathrm{\Phi }$ will have:

$\mathit{M}={\mathit{n}}^{\mathit{k}}$ (1)

elements, where $k=K$ (initially, it is assumed that exponent index k equals the nominal number of workers K, $k<K$will be also analyzed).

Such prerequisites cannot eliminate arbitrary setting of a specific state set as far as a set of actions of participants cannot be always identified without question. However, it will be shown that conclusions drawn from the quality model analysis do not depend on this ambiguity.

At each point of time, a certain state of the firm $x\in \mathrm{\Phi }$ can be observed. It is affected by the external environment. At the same point of time, the state affected by control $u\in U$ (U is a set of controls) generated by the control subsystem is transformed into another state $y\in \mathrm{\Phi }$. The control is efficient if $y\in \hat{\mathrm{\Phi }}$ – a subset of desirable states for the control subsystem $\hat{\mathrm{\Phi }}\subset \mathrm{\Phi }$, and it is inefficient if $y\in \mathrm{\Phi }\backslash \hat{\mathrm{\Phi }}$ no matter which subset the controlled state x belonged to. Let us assume that for each state $x\in \mathrm{\Phi }$, there is at least one efficient control. If the number of controls is less than the number of states, some controls will be efficient for several states.

Based on the statistics of consecutive realizations x, the entropy is determined:

$H\left(x\right)=-{\sum }_{x\in \mathrm{\Phi }}P\left(x\right)\mathrm{l}\mathrm{n}P\left(x\right)$, (2)

where $P\left(x\right)$ is the probability of realization of state x. $H\left(y\right)$ and $H\left(u\right)$were determined in a similar way.

Research Methods

Definition . The firm is controllable if $H\left(y\right)<H\left(x\right)$.

If the firm is controllable, probabilities $P\left(y\right)$, $y\in \hat{\mathrm{\Phi }}$ will be higher than in similar states $x\in \hat{\mathrm{\Phi }}$ (as far as controls aim to transform arbitrary states into desirable ones, the frequency of the latter should increase if any part of control is efficient), therefore $H\left(y\right)<H\left(x\right)$ due to elementary entropy properties following from (2). The definition agrees with the second law of thermodynamics saying that the entropy decreases in non-controllable systems.

The system’s ability to decrease entropy is expressed by the law of requisite variety (Ashby, 1958):

$\mathit{H}\mathbf{\left(}\mathit{y}\mathbf{\right)}\mathbf{\ge }\mathit{H}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{-}\mathit{I}\mathbf{(}\mathit{u}\mathbf{,}\mathit{x}\mathbf{)}$. (3)

where

$\mathit{H}\mathbf{\left(}\mathit{y}\mathbf{\right)}\mathbf{\ge }\mathit{H}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{-}\mathit{I}\mathbf{(}\mathit{u}\mathbf{,}\mathit{x}\mathbf{)}$ (4)

is the number of information in u about x , and:

$\mathit{H}\mathbf{\left(}\mathit{u}\mathbf{\right|}\mathit{x}\mathbf{)}\mathbf{=}\mathbf{-}{\sum }_{\mathit{x}\mathbf{\in }\mathbf{\Phi }}\mathit{P}\mathbf{\left(}\mathit{x}\mathbf{\right)}{\sum }_{\mathit{u}\mathbf{\in }\mathit{U}}\mathit{P}\mathbf{\left(}\mathit{u}\mathbf{\right|}\mathit{x}\mathbf{\left)}\mathbf{l}\mathbf{n}\mathit{P}\mathbf{\right(}\mathit{u}\mathbf{\left|}\mathit{x}\mathbf{\right)}$,(5)

conditional entropy. From the definition, it follows that the firm will be controllable if $I(u,x)>\mathrm{0}$.

The conditional entropy has the following properties:

$\mathit{H}\mathbf{\left(}\mathit{u}\mathbf{\right|}\mathit{x}\mathbf{)}\mathbf{=}\mathit{H}\mathbf{(}\mathit{u}\mathbf{)}$,(6)

if u and x are the independent random values and:

$\mathit{H}\left(\mathit{u}|\mathit{x}\right)\mathbf{=}\mathbf{0}$ , (7)

if there is homomorphous mapping of $\mathrm{\Phi }$ in U ( $\forall x\in \mathrm{\Phi }\exists u\in U:p\left(u\right|x)=\mathrm{1}$). In relation to (3), fulfillment of condition (6) causes loss of control as far as (4) is equal to zero, and (7) ensures accurate control. It agrees with the fact that in the information theory the conditional entropy in (4) is responsible for the channel noise.

Statement 1 (about loss of control). New elements in state set $\mathrm{\Phi }$ result in $I(u,x)\to \mathrm{0}$.

Proof. For new element $\tilde{x}\in \mathrm{\Phi }$, an efficient management decision is unknown. Therefore, fitting requires application of several different management decisions. As a result, partial conditional entropy $H\left(u\right|\tilde{x})=-{\sum }_{u\in U}P\left(u\right|\tilde{x}\left)\mathrm{l}\mathrm{n}P\right(u\left|\tilde{x}\right)$ will increase. The larger the number of new states is, the closer $I(u,x)$ to zero is.

Note 1. To solve the control task, each element of state set $\mathrm{\Phi }$ should be identified. It means that if known (not new in terms of statement 1) state $\hat{x}\in \mathrm{\Phi }$ for which efficient management decision $\hat{u}$is known has been already realized, it should be previously identified by the control system as $\hat{x}$. Wrong identification results in wrong selection of controls which will correspond to systems’ behavior in conditions of statement 1.

Identification can be presented as feedback channels between the firm and its control subsystem shown in Figure 1 as $I_x$ and $I_y$. They are typical Shannon data communications channels when identifying states x and y . Blocking of one of the channels fulfils the conditions of statement 1. In the first case, lacking possibility to identify state x , we will be searching for an efficient management decision in a random way. In the second case, without knowledge of the number of state y , we can determine whether the management decision was effective or non-effective. The above menetioned provides insight into the feedback as a uniform training channel.

See Full Size >

Statement 2 (about control recovery). Finding an effective control decision for the state, for which the identification task is solvable, ensures $I(u,x)\to H\left(u\right)$.

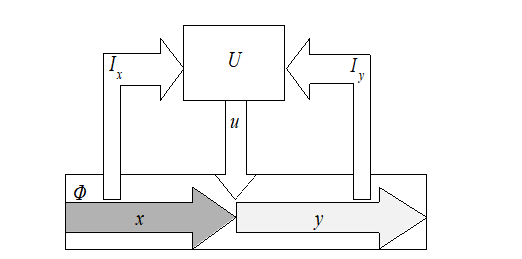
Proof. If for $\tilde{x}\in \mathrm{\Phi }$ effective management decision $\tilde{u}$ is found, only that decision will be applied. An increase in $\tilde{u}$ usage reduces the partial conditional entropy $H\left(u\right|\tilde{x})=-{\sum }_{u\in U}P\left(u\right|\tilde{x}\left)\mathrm{l}\mathrm{n}P\right(u\left|\tilde{x}\right)$.

Note 2. If there are no new elements in set $\mathrm{\Phi }$ and all the elements can be identified, control recovery processes will dominate control loss processes. As a result, during the finite number of cycles, condition (7) is fulfilled. Only in this case, the statement of the law of requisite variety (control power is determined by $H\left(u\right)$) is true.

If there is no ban on new states, one can argue that conditions in statement 1 and conditions in statement 2 act together. And it is impossible to identify which conditions are more important. However, the growing firm is a special case allowing some conclusions.

To solve an identification task, a control subsystem should know all the elements of the state set. According to the task, it is necessary to search through all the elements using data from feedback channels. Output of channels $I_x$ or $I_y$ cannot exceed a Hartley value:

${\mathit{H}}^{\mathbf{*}}\mathbf{=}\mathbf{l}\mathbf{n}\mathbf{\left(}\mathit{M}\mathbf{\right)}$.(8)

It is a maximum speed rate at which set $\mathrm{\Phi }$ can “acquaint” the control system with its elements. It does not depend on structural channel characteristics.

Statement 3 (information growth limitations). For the growing firm ( K increases), control loss occurs with speed rate (1), and control recovery – with speed rate (8), so the control loss process will dominate the control recovery process.

Proof. Comparison of (1) and (8) as multi-ordinal values shows that with increasing K associated with the firm growth, M will be ahead of $H^{\mathrm{*}}$ and it will block identification. With regard to note 1, we have the conditions of statement 1.

Note 3. The result obtained does not depend on the calculation method for number n of degrees of freedom of workers as (1) and (8) are multi-ordinal values. For this reason, the growth of the firm turns a trivial identification procedure into an unsolvable task. Statement 3 is true even if there are groups of similar states which similar effective control decisions should correspond to. So wrong identification does not result in lost control.

This effect occurs when dividing workers of a large firm into several departments with a partially autonomous set of functions. It allows elimination of a large number of states. With the same n and K , one can deal with a number which is less than M . It is evident that one can mitigate information limitations but cannot eliminate them as the larger the firm is, the more departments it has, which generates conditions of statement 3.

Statement 4 (mitigation of information limitations). Elimination of combinations, which are not required for identification from (1), results in slower growth of k in comparison with K .

As far as the analogue of (1) is the number of texts of K -length in the alphabet containing n letters, the proof is similar to the well-known statement of the information theory which says that if one deals with only meaningful texts, their number will be expressed with the same exponent with index $k<K$.

Findings

The information limitation model is based on the assumption that maximum feedback channel output $H^{\mathrm{*}}=\mathrm{l}\mathrm{n}\left(M\right)$ (8) is not enough for solving state identification tasks. Its real output will be lower than the maximum one. So, along with the direct control working for increasing $H\left(u\right)$, it is crucial to increase the output of training channels $I_x$, $I_y$ working for decreasing control losses expressing as $H\left(u\right|x)$.

In the information theory, it is referred to as the first variation task. It determines distributions contributing to the maximum output:

$S=\underset{P\left(x\right)}{\max }H\left(x\right)$, (9)

if there is a penalty function:

${\sum }_{x\in \mathbf{\Phi }}c\left(x\right)P\left(x\right)\le C,\mathrm{}$(10)

where $c\left(x\right)$ are the information costs connected with state x (information state processing costs), C – limit of information costs of the firm, i.e. total resources used to increase a training channel output.

The first variation task was borrowed from thermodynamics where it is formulated in a dual form as entropy maximization when limiting system’s energy. It is a statement of the second law of thermodynamics. It is known that analytical solution of the task dual of (9)-(10) involves Gibbs distribution:

$P\left(x\right)=e^{\frac{G-c\left(c\right)}{T}}$, (11)

where

$G=-T\ln Z;Z=\underset{X}{\sum }{e}^{-c\left(x\right)/T}$.(12)

G is the free energy, T is the temperature. For the free energy, thermodynamics uses one more expression:

$G=C-TS$,(13)

which is a Lagrange function with multiplier T for the task dual of (9)-(10).

In its theoretical and information interpretation, the first variation task involves an economic dilemma: ensure a maximum information output (9) within a resource value (10). In any optimization economic task, Lagrange multipliers are prices of distributed resources. As far as information is a resource, T is interpreted as an information price.

If T is positive, one can change limitations on information costs in the range of:

$C\in \left(\underset{x}{\mathrm{m}\mathrm{i}\mathrm{n}}c\left(x\right),\frac{\mathrm{1}}{M}{\sum }_{x}c\left(x\right)\right)$,(14)

not violating the task consistency (9)-(10), where M is (1). The correlation:

$\frac{dC}{dS}=T$(15)

shows that S is the increasing function C . Thus, values:

$S\in (\underset{\_}{S},H^{\mathrm{*}})$(16)

will correspond to variability C in the range of (11) where $H^{\mathrm{*}}=\mathrm{l}\mathrm{n}\left(M\right)$ is the amount of information (8), $\underset{\_}{S}\ge \mathrm{0}$ is the low entropy limit.

From (9)–(13), relations S and T and C can be presented as curvatures in Figure 2 . Coordinates of points M and N are determined by intervals (14) and (16). S directed to the upper boundary is accompanied by an increase in costs C which is of a prohibitive nature because $T\to \mathrm{\infty }$.

See Full Size >

The curvature in Figure 2 characterizes decreasing limiting efficiency of output S in relation to costs C. It is reasonable as increasing information costs contribute to the growing profit. The information model says that effective information costs contribute to the growing profit by means of the firm growth as a result of better management.

Conclusion

The model explains a number of empirical phenomena. Expression (1) determines the number of elements of a state set as $M=n^k$. It will grow fast (exponentially) by k and slower (polinomially) - by n, so a decrease in the exponent will have the maximum effect on mitigating information limitations on the growth. At first, a growing firm develops as an organizational structure. Then, firm activities (whose number is n) have to be controlled. Increasing bureaucratization and regulation are typical of large companies 0.

Parameter n is determined by endogenic and exogenic factors. For example, the number of processes for an oil company is less than the number of processes for a footwear firm due to the fact that consumer requirements for shoes are higher than requirements for oil products. Therefore, footwear firms have a higher n value than oil companies, as a result the latter are larger than footwear firms. This trend can be observed in the industrial structure of company ratings where oil and financial companies hold upper lines. That industrial selection cannot be described by the theory of specific assets.

One more conclusion can be drawn from the model: the control loss is not caused by relations of principals and agents. Loyal activities of agents have no effects on control loss processes while the theory of agents is based on the opportunistic behavior assumption.

The model also deals with the issue of an optimum firm size. If the size were dependent on economies of scale and its loss, U-curvature of costs would signal an optimum firm size around which the costs would center. However, according to researches, Zipf’s law can explain the firm size distribution 0. The law is consistent with the curvature of an optimum output of the information cost model. Thus, the statistics says that the concept of an optimum firm size is useless.

References

1. Acemoglu, D., Dorn, D., Hanson, G. H., Price, B. (2014). Return of the Solow paradox? IT, productivity, and employment in US manufacturing. The American Economic Review, 104(5), 394-399.
2. Ashby W. R. (1958) Requisite variety and its implications for the control of complex systems, Cybernetics, 1(2), 83-99.
3. Axtell R. (2001). Zipf Distribution of U.S. Firm Sizes. Science, 293(5536), 1818–1820.
4. Beck, T., Demirgüç-Kunt, A., Maksimovic, V. (2005). Financial and legal constraints to growth: does firm size matter? The Journal of Finance, 60(1), 137-177.
5. Brynjolfsson, E. (1993). The productivity paradox of information technology: review and assessment. Communications of the ACM, 36(12).
6. Canbäck, S., Samouel Ph., Price, D. (2006). Do Diseconomies of Scale Influence Firm Size and Performance? A Theoretical and Empirical Overview. Journal of Managerial Economics, 4(1), 27-7
7. Coase, R. (1937). The Nature of the Firm. Economics, 4(16), 356-405.
8. Fox, J. (2009) Firm-Size Wage Gaps, Job Responsibility, and Hierarchical Matching. Journal of Labor Economics, 27(1), 83-126.
9. Hart, O. (1989). An economist's perspective on the theory of the firm. Colombia Law Review, 89(7), 57-74.
10. Holmström, B., Roberts, J. (1998). The Boundaries of the Firm Revisited. Journal of Economic Perspectives, 12(4), 73–94.
11. Jensen, M., Meckling W. (1976). Theory of the firm: managerial behavior, agency costs and ownership structure. Journal of Financial Economics, 3(4), 303–360.
12. Klein, B., Krawford R., Alchian A. (1978). Vertical integration, appropriable rents, and the competitive contracting process. Journal of Law and Economics, 21(2), 297-326.
13. Kumar, K., Rajan, R., Zingales, L. (1999). What Determines Firm Size? Working paper, NBER, No. w7208.
14. Matejka, F., McKay, A. (2014). Rational inattention to discrete choices: A new foundation for the multinomial logit model. The American Economic Review, 105(1), 272-298.
15. Triplett, J. E. (1999). The Solow productivity paradox: what do computers do to productivity? The Canadian Journal of Economics/Revue canadienne d'Economique, 32(2), 309-334.
16. Williamson, O. (1967). Hierarchical Control and Optimum Firm Size. Journal of Political Economy, 75(2), 123-138.
17. Williamson, O. (1971). The Vertical Integration of Production: Market Failure Consideration. American Economic review. 61(2), 112-123.